Monotoniebereiche von Funktionen bestimmen
Entdecke das Monotoniekriterium für differenzierbare Funktionen! Finde heraus, wann eine Funktion monoton steigt oder fällt und übe mit Beispielen. Interessiert? Dies und vieles mehr findest du im folgenden Video!
in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
Lerntext zum Thema Monotoniebereiche von Funktionen bestimmen
Was sind Monotoniebereiche?
Mit dem Monotonieverhalten wird in der Mathematik die Steigung eines Funktionsgraphen bezeichnet.
Es gibt vier verschiedene Möglichkeiten für das Steigungsverhalten eines Graphen:
- streng monoton steigend: Der Graph ist nur steigend.
- monoton steigend: Der Graph ist steigend oder hat die Steigung null.
- streng monoton fallend: Der Graph ist nur fallend.
- monoton fallend: Der Graph ist fallend oder hat die Steigung null.
Viele Funktionen zeigen nicht im gesamten Definitionsbereich das gleiche Steigungsverhalten, sondern sind in einigen Bereichen steigend und in anderen fallend. Daher gibt man Intervalle (also Bereiche bzw. Abschnitte der $x$-Achse) an, in denen der Graph die gleiche Monotonie aufweist. Wenn z. B. der Graph von $f$ zwischen zwei $x$-Werten $a$ und $b$ nur steigt, schreibt man das so: „$f$ ist streng monoton steigend im Intervall $]a,b[$.“ Das heißt, der Graph ist streng monoton steigend für alle $x$-Werte mit $a\lt x\lt b$, denn es handelt sich um ein offenes Intervall, in dem die Zahlen $a$ und $b$ nicht enthalten sind.
Wie kann man Monotoniebereiche berechnen?
Das Steigungsverhalten eines Graphen an einer bestimmten Stelle wird durch die Tangentensteigung bzw. erste Ableitung angezeigt:
- An Stellen ohne Steigung hat der Graph eine waagerechte Tangente und es gilt $f^\prime (x)=0$.
- An Stellen mit positiver Steigung hat der Graph eine steigende Tangente und es gilt $f^\prime (x)\gt 0$.
- An Stellen mit negativer Steigung hat der Graph eine fallende Tangente und es gilt $f^\prime (x)\lt 0$.
Daher kann man den Zusammenhang zwischen dem Monotonieverhalten im Intervall $]a,b[$ und dem Vorzeichen der ersten Ableitung für $a\lt x\lt b$ wie in folgender Tabelle zusammenfassen:
| Monotonieverhalten | Vorzeichen der Ableitung |
|---|---|
| streng monoton steigend | $f^\prime (x)\gt 0$ |
| monoton steigend | $f^\prime (x)\geq 0$ |
| streng monoton fallend | $f^\prime (x)\lt 0$ |
| monoton fallend | $f^\prime (x)\leq 0$ |
Um das Monotonieverhalten einer Funktion zu bestimmen, muss man also untersuchen, in welchen Bereichen die erste Ableitung positiv, negativ oder null ist.
Das Vorgehen lässt sich in vier kleine Schritte unterteilen:
- Bestimme die erste Ableitung von $f$.
- Berechne die Nullstellen der ersten Ableitung.
- Teile den Definitionsbereich der Funktion in Teilintervalle entsprechend der Nullstellen ein.
- Bestimme mithilfe der ersten Ableitung die Monotonie in jedem Intervall.
Bestimmung von Monotoniebereichen – Beispielaufgaben
Um die Aufgaben nachzuvollziehen, solltest du schon wissen, wie man die erste Ableitung einer Funktion bestimmt (u. a. mit der Potenz-, Faktor- und Summenregel) und wie man Nullstellen berechnet (z. B. mit der $pq$-Formel).
Beispiel 1 – Funktion mit zwei Extrempunkten
Bestimme die Monotoniebereiche von $f(x)=x^{3}+3x^{2}-24x$.
Bilde die erste Ableitung:
$f^\prime(x)=3x^{2}+6x-24$
Bestimme die Nullstellen:
$\begin{array}{cclr}f^\prime(x) & = & 0 \\ 3x^2+6x-24 & = & 0 & \vert :3\newline \\ x^2+2x-8 & = & 0 \end{array}$
$x_{1,2}=-\frac{2}{2}\pm \sqrt{\left (\frac{2}{2}\right )^{2}-(-8)}=-1 \pm \sqrt{9}=-1 \pm 3$
$\implies x_{1}=-4 \text{ und } x_{2}=2$
Gib die Teilintervalle an:
Die Funktion ist auf ganz $\mathbb{R}$ definiert, der Definitionsbereich geht also von $-\infty$ bis $+\infty$ und wird durch die Nullstellen $x_{1}=-4$ und $x_{2}=2$ in drei Bereiche unterteilt: $]-\infty, -4[$ und $] -4, 2[$ und $] 2, \infty[$.
Bestimme die Monotonie in jedem Intervall:
Setze aus jedem Intervall eine Zahl in die erste Ableitung ein und prüfe, welches Vorzeichen das Ergebnis hat. Welche Zahl du auswählst, ist beliebig, allerdings musst du darauf achten, dass es sich um offene Intervalle handelt, das heißt, die Intervallgrenzen gehören nicht zum Intervall und dürfen nicht eingesetzt werden (in diesem Fall $-4$ und $2$).
$f^\prime(-10)=3\cdot(-10)^2+6\cdot(-10)-24=216\newline \implies f^\prime(-10)\gt 0$
$f^\prime(1)=3\cdot 1^2+6\cdot 1-24=-15\newline \implies f^\prime(1)\lt 0$
$f^\prime(10)=3\cdot 10^2+6\cdot 10-24=336\newline \implies f^\prime(10)\gt 0 $
Die Ergebnisse sind in der Tabelle zusammengefasst, vergleiche diese mit der Skizze des Graphen.
| Intervall | $]-\infty, -4[$ | $] -4, 2[$ | $] 2, \infty[$ |
|---|---|---|---|
| Monotoniebestimmung mit der ersten Ableitung | $f^\prime(-10)\gt 0$ | $f^\prime(1)\lt 0 $ | $f^\prime(10)\gt 0$ |
| Monotonieverhalten | streng monoton steigend | streng monoton fallend | streng monoton steigend |
Übrigens kann man anhand der Monotoniebereiche auch die Art der Extremstellen des Graphen ablesen: An der Stelle, an der sich die Monotonie von steigend nach fallend ändert, ist ein Hochpunkt und an der Stelle, an der sich die Monotonie von fallend nach steigend ändert, ist ein Tiefpunkt. Diese Tatsache macht sich das Vorzeichenwechselkriterium zunutze.
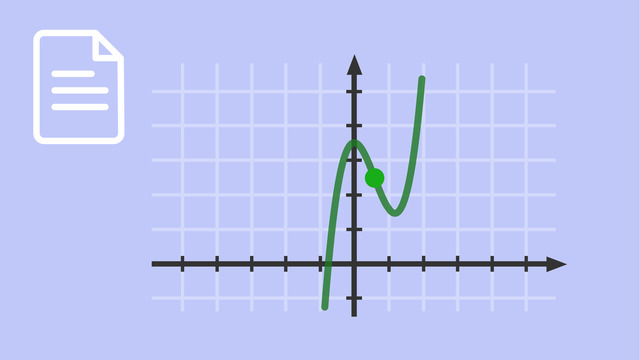
Beispiel 2 – Funktion mit Sattelpunkt
Bestimme die Monotoniebereiche von ${f(x)=2x^{3}-18x^{2}+54x}$.
Bilde die erste Ableitung:
$f^\prime(x)=6x^{2}-36x+54$
Bestimme die Nullstellen:
$\begin{array}{cclr}f^\prime(x) & = & 0 \\ 6x^2-36x+54 & = & 0 & \vert :6 \\ x^2-6x+9 & = & 0 \end{array}$
$x_{1,2}=-\frac{-6}{2}\pm \sqrt{\left (\frac{-6}{2}\right )^{2}-9}=3 \pm \sqrt{0}=3 \pm 0$
$\implies x=3$
Gib die Teilintervalle an:
Die Funktion ist auf ganz $\mathbb{R}$ definiert, der Definitionsbereich geht also von $-\infty$ bis $+\infty$ und wird durch die Nullstelle $x=3$ in zwei Bereiche unterteilt: $]-\infty, 3[$ und $] 3, \infty[$.
Bestimme die Monotonie in jedem Intervall:
Setze aus jedem Intervall eine Zahl in die erste Ableitung ein und prüfe, welches Vorzeichen das Ergebnis hat.
$f^\prime(0)=6\cdot 0^{2}-36\cdot 0+54=54\newline \implies f^\prime(0)\gt 0$
$f^\prime(10)=6\cdot 10^{2}-36\cdot 10+54=294\newline \implies f^\prime(10)\gt 0$
Die Ergebnisse sind in der Tabelle zusammengefasst. Vergleiche diese mit der Skizze des Graphen.
| Intervall | $]-\infty, 3[$ | $] 3, \infty[$ |
|---|---|---|
| Monotoniebestimmung mit der ersten Ableitung | $f^\prime(0)\gt 0 $ | $f^\prime(10)\gt 0 $ |
| Monotonieverhalten | streng monoton steigend | streng monoton steigend |
Da das Monotonieverhalten sich nicht ändert, ist der Graph im gesamten Definitionsbereich ${]-\infty, \infty[}$ monoton steigend – aber nicht streng monoton steigend, weil der Graph an der Stelle $x=3$ die Steigung $0$ hat.
Außerdem kann man ablesen, dass der Graph keine Extremstelle bei $x=3$ hat, da die Monotonie links und rechts von der Stelle steigend ist. Der Graph hat an dieser Stelle einen Sattelpunkt.
Monotoniebereiche von Funktionen bestimmen Übung
-
Benenne den Zusammenhang zwischen Monotonie und erster Ableitung.
TippsWenn ein Steigungsverhalten monoton, aber nicht streng monoton ist, dann ist ein waagerechter Verlauf ($f^\prime (x)=0$) enthalten.
LösungDie richtige Zuordnung lautet:
streng monoton steigend: $f^\prime (x)\gt 0$
monoton steigend: $f^\prime (x)\geq 0$
streng monoton fallend:$f^\prime (x)\lt 0$
monoton fallend: $f^\prime (x)\leq 0$
-
Bestimme die erste Ableitung.
TippsVier Rechnungen enthalten Fehler.
LösungFolgende Ableitungen wurden falsch gebildet:
- $f(x)=\frac{1}{6}x^6-\frac{1}{25}x^5$
richtig: $f^{\prime}(x)=x^5-\frac{1}{5}x^4$
- $f(x)=-3x^5+5x^3+15x$
richtig: $f^{\prime}(x)=-15x^4+15x^2+15$
- $f(x)=x^{-3}$
richtig: $f^{\prime}(x)=-3x^{-4}$
- $f(x)=3x^3-9x-9$
richtig: $f^{\prime}(x)=9x^2-9$
-
Bestimme die Nullstellen und Teilintervalle der Funktionen.
TippsBestimme die Nullstellen der ersten Ableitung, um die Grenzen der Teilintervalle herauszufinden.
Lösung- $f(x)=x^2+2x-8$
Nullstellen: $f^{\prime}(x)=0 \implies 2x+2=0 \implies \underline{\underline{x=-1}}$
Teilintervalle: $]-\infty,-1[ \quad \text{ und }\quad ]-1,\infty[$
- $f(x)=x^2+1$
Nullstellen: $f^{\prime}(x)=0 \implies 2x=0 \implies \underline{\underline{x=0}}$
Teilintervalle: $]-\infty,0[ \quad \text{ und }\quad ]0,\infty[$
- $f(x)=x^2-2x$
Nullstellen: $f^{\prime}(x)=0 \implies 2x-2=0 \implies \underline{\underline{x=1}}$
Teilintervalle: $]-\infty,1[\quad \text{ und }\quad ]1,\infty[$
- $f(x)=x^3-3x^2$
Nullstellen: $f^{\prime}(x)=0 \implies 3x^2-6x=0 \implies x(3x-6)=0 \implies \underline{\underline{x_1=0}} \text{ und } \underline{\underline{x_2=2}}$
Teilintervalle: $]-\infty,0[ \quad \text{ und }\quad ]0,2[ \quad \text{und} \quad ]2,\infty[$
-
Bestimme die Monotoniebereiche der Funktion.
TippsSetze eine beliebige Zahl aus dem Intervall in die erste Ableitung und prüfe das Vorzeichen, um das Monotonieverhalten in diesem Intervall angeben zu können.
LösungSchritt 1 Ableitung der Funktion
$f^{\prime}(x)=3x^2-12x$
Schritt 2 Nullstellen der Ableitung
$f^{\prime}(x)=0 \implies 3x^2-12x=0 \vert :3$
$x^2-4x=0$
$\implies x_1=0 \text{ und } x_2=4$
Schritt 3 Aufteilung in Teilintervalle
$]-\infty, 0[ \quad \text{ und } \quad ]0,4[ \quad \text{ und } \quad ]4, \infty[$
Schritt 4 Bestimmung der Monotoniebereiche (hierfür beliebige Punkte aus den jeweiligen Intervallen in die Funktionsgleichung der ersten Ableitung einsetzen)
- $f$ ist im Intervall $]-\infty, 0[ $ streng monoton steigend
- $f$ ist im Intervall $]0,4[$ streng monoton fallend
- $f$ ist im Intervall $]4, \infty[ $ streng monoton steigend
-
Beschreibe das Vorgehen zur Bestimmung des Monotonieverhaltens.
TippsUm das Monotonieverhalten einer Funktion zu bestimmen, muss man untersuchen, in welchen Bereichen die erste Ableitung positiv, negativ oder null ist.
LösungDas Vorgehen lässt sich in vier Schritte unterteilen:
- Bestimme die erste Ableitung von $f$.
- Berechne die Nullstellen der ersten Ableitung.
- Teile den Definitionsbereich der Funktion in Teilintervalle entsprechend der Nullstellen ein.
- Bestimme mit Hilfe der ersten Ableitung die Monotonie in jedem Intervall.
-
Bestimme das Monotonieverhalten der Funktion.
TippsIst $f^{\prime}(x)<0$ für $x \in ]a,b[$, dann ist der Graph in $]a,b[$ streng monoton fallend.
LösungDie Ableitung lautet $f^{\prime}(x)=6x^2-24x+24$ und hat eine Nullstelle bei $x=2$.
Wir untersuchen die Teilintervalle $]-\infty, 2[ \quad $ und $\quad ]2, \infty[$.
Um die Monotonie im ersten Intervall zu prüfen, berechnen wir $f^{\prime}(1)=$, also gilt für $x \in ]-\infty, 2[: f^{\prime}(x) >0$ und die Funktion ist in diesem Intervall streng monoton steigend.
Um die Monotonie im zweiten Intervall zu prüfen, berechnen wir $f^{\prime}(5)=54$, also gilt für $x \in ] 2, \infty[: f^{\prime}(x) ${>}$0$ und die Funktion ist in diesem Intervall streng monoton steigend.
Hinweis: Da die Funktion in beiden Teilintervallen streng monoton steigend ist und bei $x=2$ die Steigung null ist, kann man auch sagen: Die Funktion ist im gesamten Definitionsbereich monoton steigend (aber nicht streng monoton steigend).

Einführung in die Kurvendiskussion

Extrema – Minimum und Maximum

Notwendige und hinreichende Bedingung für Extrema

Das Vorzeichenwechselkriterium für Extrema

Extrempunkte bestimmen – Beispiele

Verhalten ganzrationaler Funktionen im Unendlichen

Nullstellen durch Polynomdivision bestimmen

Nullstellen durch Substitution bestimmen

Nullstellen von Funktionen höheren Grades

Symmetrie von Funktionsgraphen

Achsensymmetrie und Punktsymmetrie nachweisen

Sattelpunkt berechnen

Monotoniebereiche von Funktionen bestimmen

Definitionsbereich von Funktionen

Kurvendiskussion – Übungen
Wendepunkte berechnen
9.836
sofaheld-Level
6.600
vorgefertigte
Vokabeln
8.306
Lernvideos
38.657
Übungen
33.694
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Klassenstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung


 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?












