Schriftlich und halbschriftlich dividieren

Inhaltsverzeichnis zum Thema

• Was ist die Division?
• Halbschriftliche Division
• Schriftliche Division
• Schriftliche Division mit Rest

Was ist die Division?

Die Division ist eine der vier Grundrechenarten. Du weißt sicher, dass 6 : 3 = 2 ist. Die Antwort auf „Was ist das Ergebnis von 6 : 3?“ erhältst du, wenn du dir überlegst, wie oft die 3 in die 6 passt. Die Antwort ist zwei Mal, da 2 $\cdot$ 3 = 6 ist. Die Division ist eine Punktrechnung. Der Doppelpunkt zeigt an, dass dividiert oder auch geteilt wird.

6 : 3 = 2, dabei ist

• 6 der Dividend, der Teil der Division, der geteilt wird.
• 3 der Divisor, der Teil der Division, durch den geteilt wird.
• 2 der Quotient, das Ergebnis der Division.

Merke dir zur Division: Dividend durch Divisor gleich Quotient.

Bei solchen Aufgaben wie zum Beispiel 6 : 3 = 2 oder 15 : 5 = 3 kannst du dir immer umgekehrt überlegen, wie oft die 3 in die 6 oder die 5 in 15 passt. Was tust du allerdings, wenn der Dividend oder vielleicht auch der Divisor eine größere Zahl ist? Tipp: Wenn du mit Überschlag dividierst oder generell rechnest, dann kannst du dein Ergebnis gerade bei großen Zahlen leichter prüfen.

Halbschriftliche Division

Stell dir vor, dass 12344 der Dividend und der Divisor 4 sind. Wie kannst du dann das Ergebnis, den Quotienten, berechnen? Wie oft passt die 4 in 12344? Weißt du vielleicht auswendig, womit du 4 multiplizieren musst, damit 12344 herauskommt? Um das Ergebnis dieser Divisionsaufgabe zu berechnen, kannst du so rechnen:

Beim halbschriftlichen Dividieren zerlegst du den Dividenden in die Zehntausender (ZT), die Tausender (T), die Hunderter (H), die Zehner (Z) und die Einer (E) und teilst jeden davon durch 4.

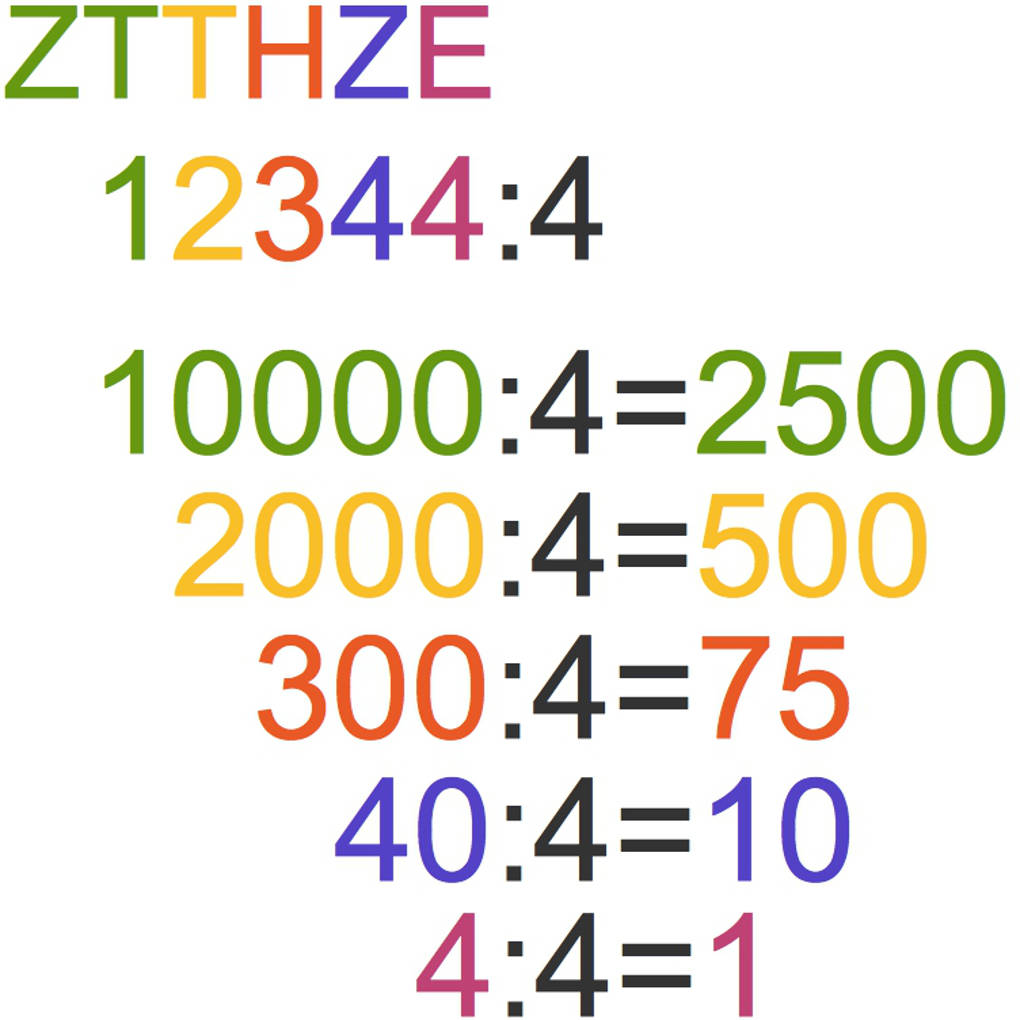
Das Ergebnis der Aufgabe 12344 : 4 erhältst du, indem du alle Ergebnisse, die Quotienten, addierst:

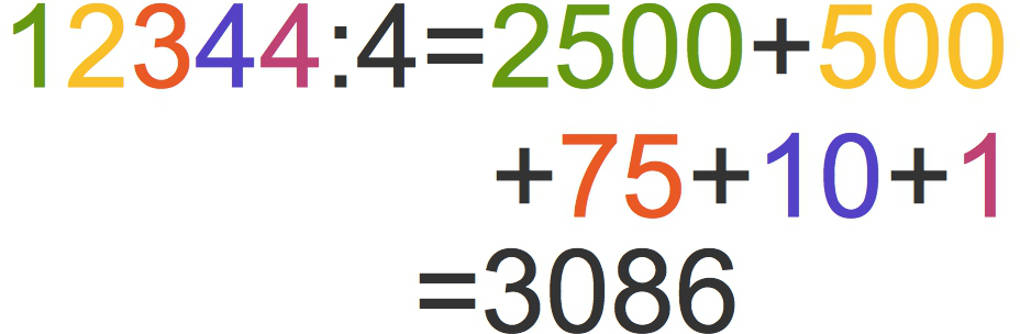
Die Division ist durch das Zerlegen in die einzelnen Stellen nicht immer ohne Rest möglich. Wenn du 12345 : 3 berechnen sollst, erhältst du bei dem Zehntausender 10000 : 3 = 3333,333... . Dies ist keine natürliche Zahl. Dann hilfst du dir mit einem Trick, indem du in die nächstkleinere Einheit zerlegst: Statt in 1 Zehntausender und 2 Tausender zerlegst du in 12 Tausender:

• 12000 : 3 = 4000
• 300 : 3 = 100
• 45 : 3 = 15

Der Quotient ist also 4115. Wie du siehst, war auch 40 nicht in 3 zerlegbar und wir haben wieder den Trick angewandt.

Schriftliche Division

Du kannst den Quotienten auch durch schriftliches Dividieren ermitteln. Dabei teilst du beim Dividenden immer die Stellen von links nach rechts durch den Divisor:

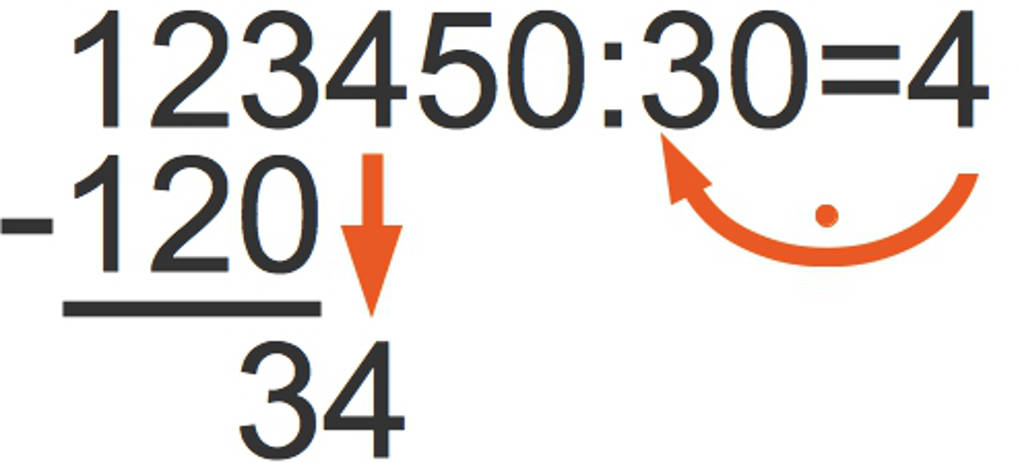
Der Divisor 30 passt nicht in 1 oder 12, aber 4 Mal in 123. Nun rechnest du 4 $\cdot$ 30 =120 und subtrahierst das Ergebnis von den ersten Stellen im Dividenden. Es bleibt ein Rest 3. Du nimmst die nächste Stelle des Dividenden, 4, mit nach unten.

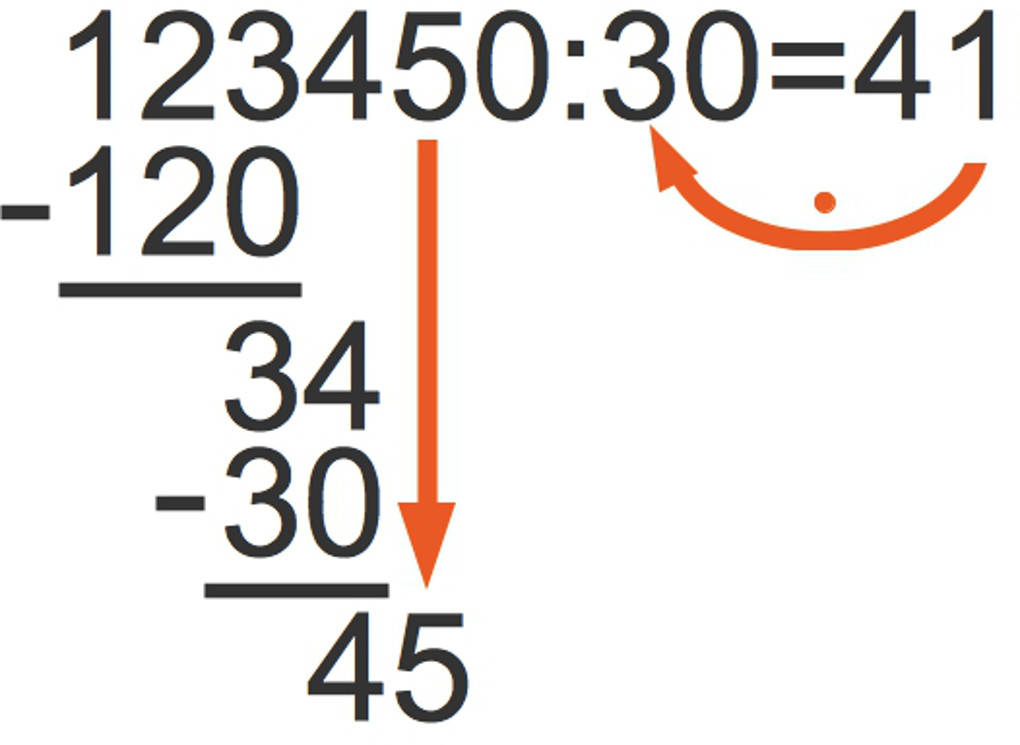
Der Divisor passt 1 Mal in 34 rein. Dann ziehst du 1 $\cdot$ 30 = 30 von 34 ab. Es bleibt ein Rest 4. Nun nimmst du von oben die nächste Stelle des Dividenden, die 5, dazu.

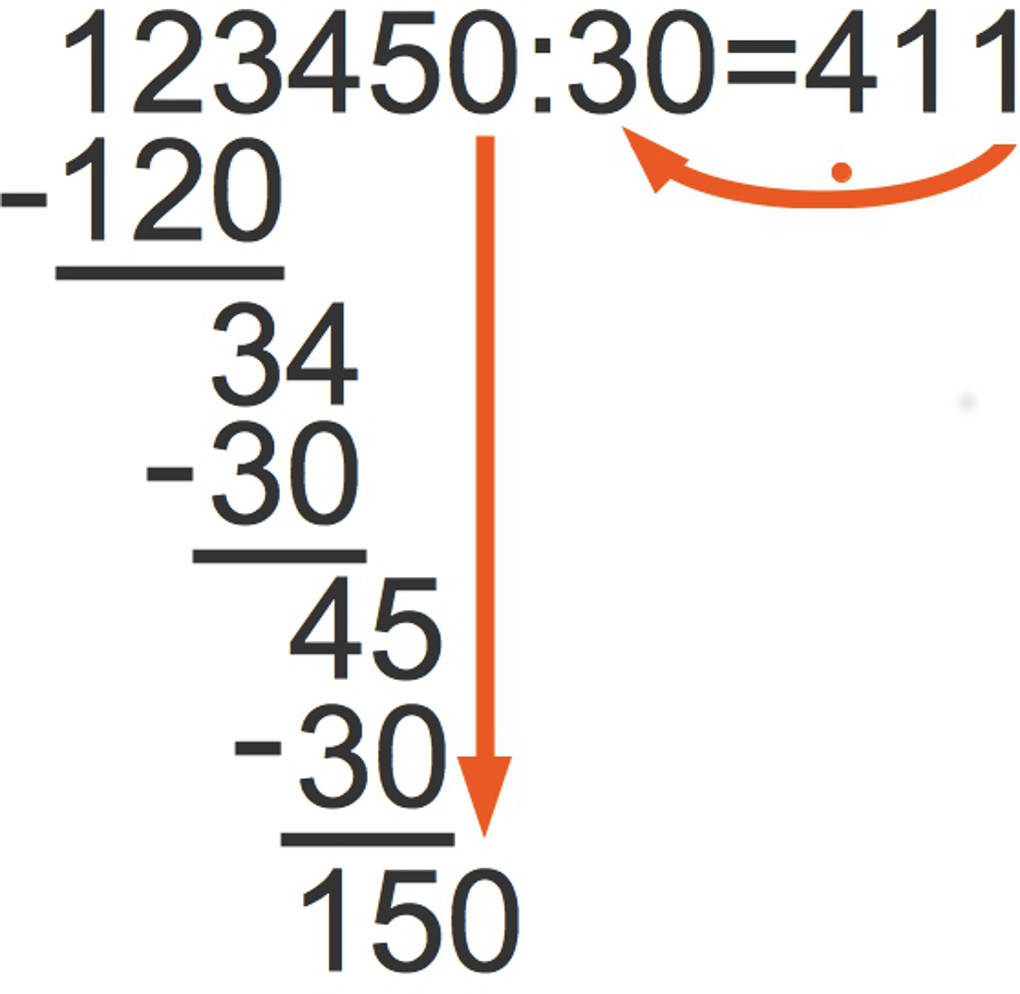
Der Divisor passt 1 Mal in 45 rein. Wieder multiplizierst du 1 $\cdot$ 30 = 30 und ziehst dies von 45 ab. Es bleibt ein Rest 15. Nun nimmst du von oben die letzte Stelle, 0, dazu.

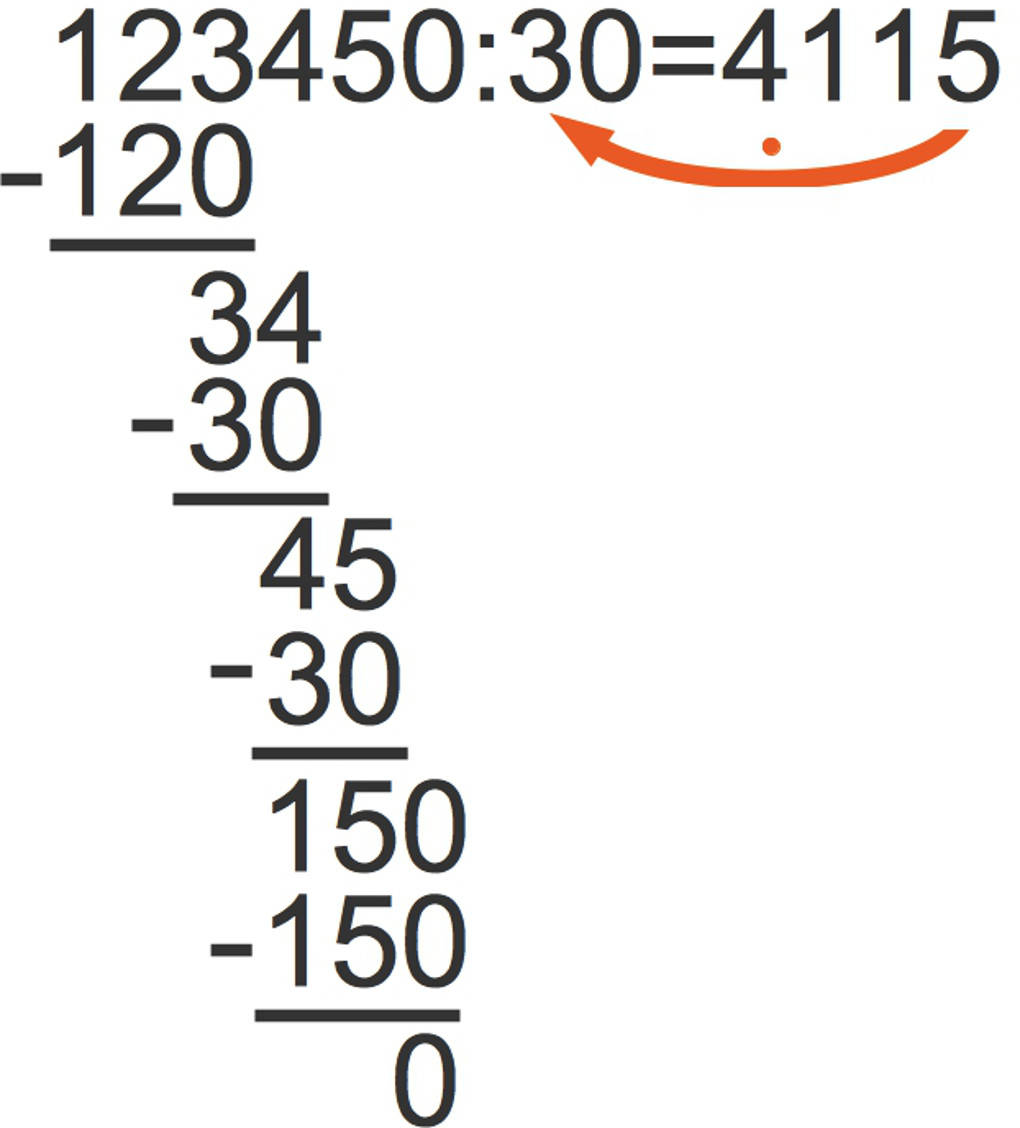
Der Divisor passt 5 Mal in 150 rein. Du multiplizierst 5 $\cdot$ 30 = 150 und erkennst, dass der Rest in diesem Beispiel 0 ist. Der Quotient ist also 4115.

Natürlich muss der Rest nicht immer 0 sein, wie du bei dem folgenden Beispiel sehen kannst.

Schriftliche Division mit Rest

Gerade bei Alltagsbeispielen geht die Division oft nicht ohne Rest auf:

Paul hat zu seinem Geburtstag insgesamt 125 Schokokäfer geschenkt bekommen. Diese möchte er gleichmäßig auf 7 Personen aufteilen:

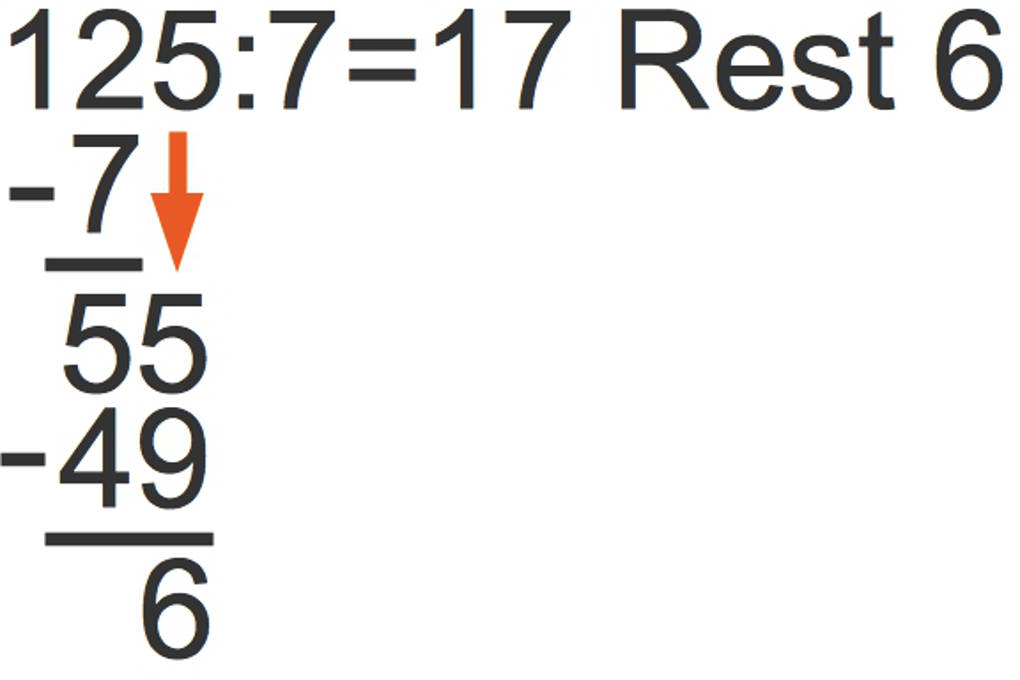
Paul kann jeder der 7 Personen 17 Schokokäfer geben. Es bleiben dann 6 Schokokäfer übrig.