Quadratische Funktionen: Scheitelpunkt und Scheitelpunktform
Der Scheitelpunkt einer quadratischen Funktion ist deren tiefster oder höchster Punkt. Hier lernst du, wie der Scheitelpunkt bestimmt wird und was man unter der Scheitelpunktform einer quadratischen Funktion versteht. Anschließend lernst du, die Scheitelpunktform aufzustellen.
Beliebteste Videos und Lerntexte
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Was ist eine quadratische Funktion
- Was ist der Scheitelpunkt einer quadratischen Funktion?
- Wie lautet die Scheitelpunktform einer quadratischen Funktion?
- Welchen Einfluss haben die Parameter der Scheitelpunktform auf die Parabel?
- Parameter $a$
- Parameter $e$
- Parameter $d$
Was ist eine quadratische Funktion
Die Scheitelpunktform ist eine spezielle Form einer quadratischen Funktion, aus der man den Scheitelpunkt der zugehörigen Parabel direkt ablesen kann. Eine quadratische Funktion ist eine ganzrationale Funktion vom Grad $2$. Die allgemeine Form einer quadratischen Funktion lautet wie folgt:
$f(x)=ax^2+bx+c$
Dabei muss $a\neq 0$ sein. Der Graph einer quadratischen Funktion ist eine Parabel. Hier siehst du zum Beispiel den Graphen der Funktion $f(x)=x^2$, die sogenannte Normalparabel.
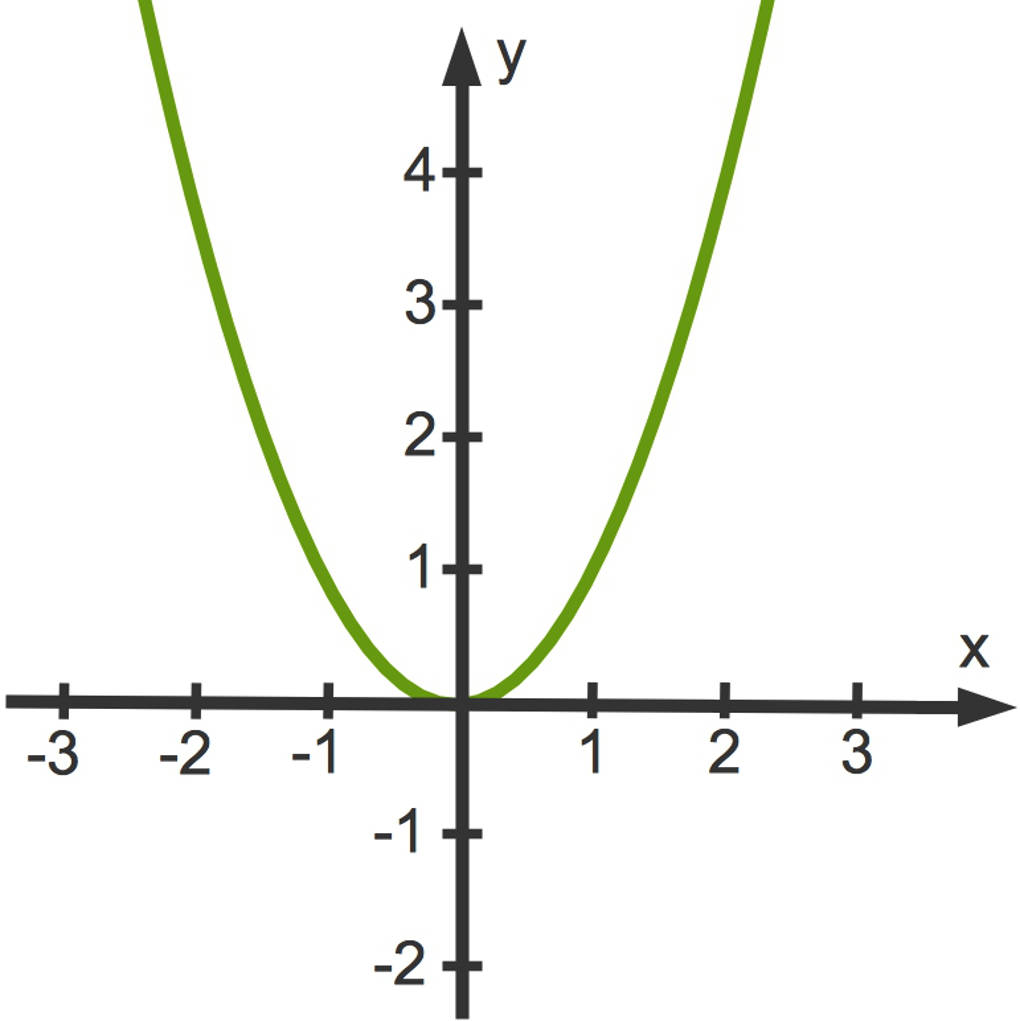
Wie du hier erkennen kannst,
- ist diese Parabel nach oben geöffnet und
- achsensymmetrisch. Die Symmetrieachse ist hier die $y$-Achse. Die Symmetrieachse verläuft bei nach oben geöffneten Parabeln durch den tiefsten Punkt der Parabel.
Eine Parabel kann auch nach unten geöffnet sein. Dann verläuft die Symmetrieachse durch den höchsten Punkt der Parabel.
Was ist der Scheitelpunkt einer quadratischen Funktion?
Der Scheitelpunkt einer nach oben (unten) geöffneten Parabel ist deren tiefster (höchster) Punkt. Durch den Scheitelpunkt verläuft die Symmetrieachse der Parabel.
Im Beispiel oben liegt der Scheitelpunkt bei $\text{S}(0\vert 0)$.
Wie lautet die Scheitelpunktform einer quadratischen Funktion?
Eine quadratische Funktion kann auch in Scheitelpunktform gegeben sein. Diese lautet wie folgt:
$f(x)=a(x-d)^2+e$
Der Scheitelpunkt $S(d|e)$ kann dieser Form direkt entnommen werden.
Welchen Einfluss haben die Parameter der Scheitelpunktform auf die Parabel?
Parameter $a$
Der Parameter $a$ mit $a\neq 0$ ist der Streckfaktor:
- für $|a|>1$ wird die Parabel gestreckt und
- für $|a|<1$ gestaucht.
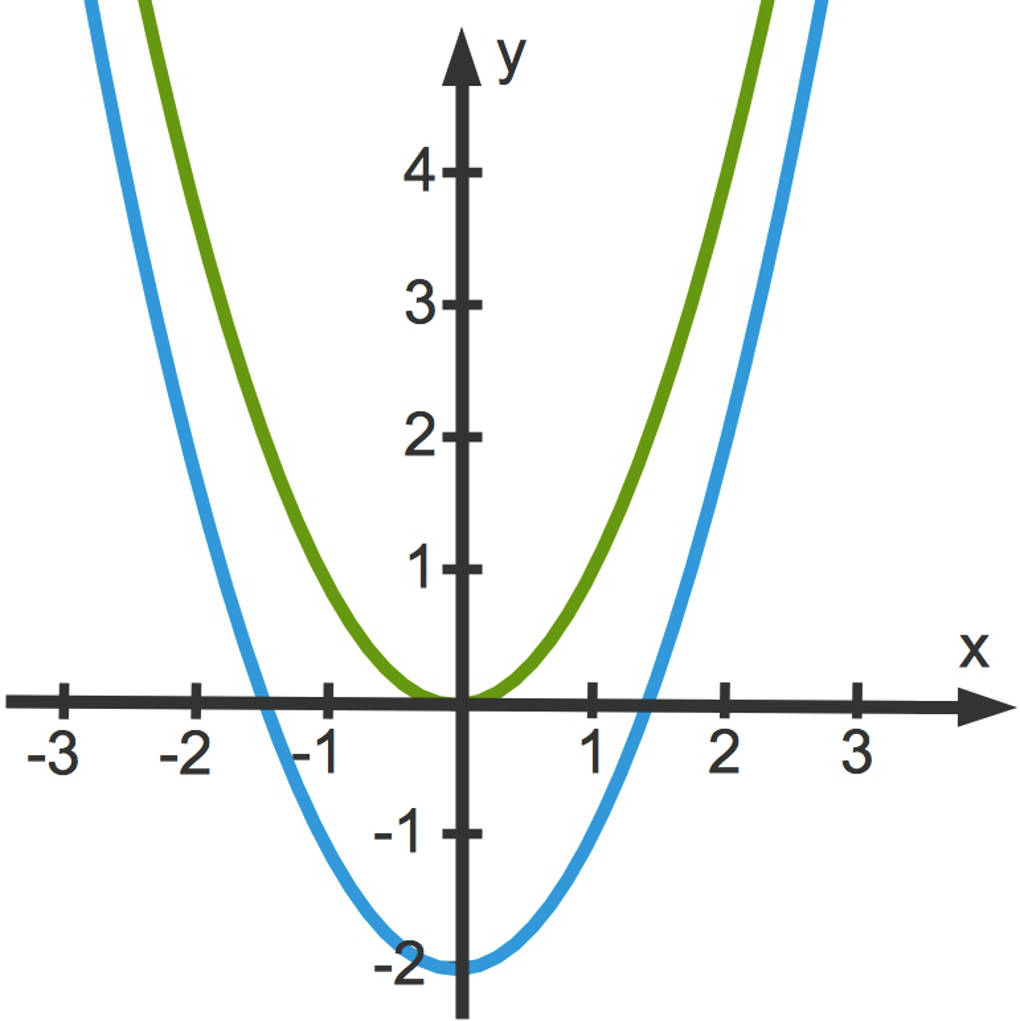
Betrachte als Beispiel für $|a|<1$ die Funktion $f(x)=0,5x^2$. Die zugehörige (rote) Parabel ist breiter als die (grüne) Normalparabel.
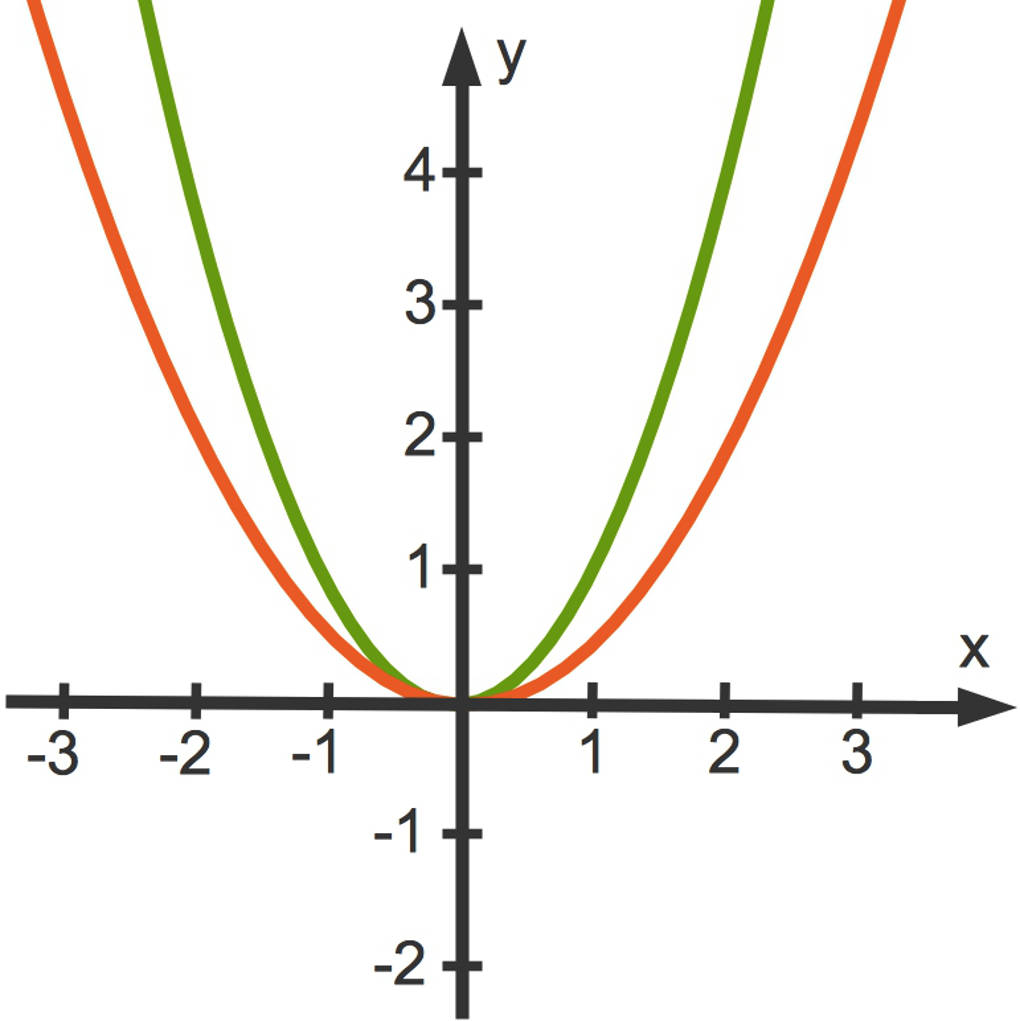
Wenn der Streckfaktor im Betrag größer ist als $1$, so ist als Beispiel die (blaue) Parabel zu $f(x)=3x^2$ schmaler als die (grüne) Normalparabel.
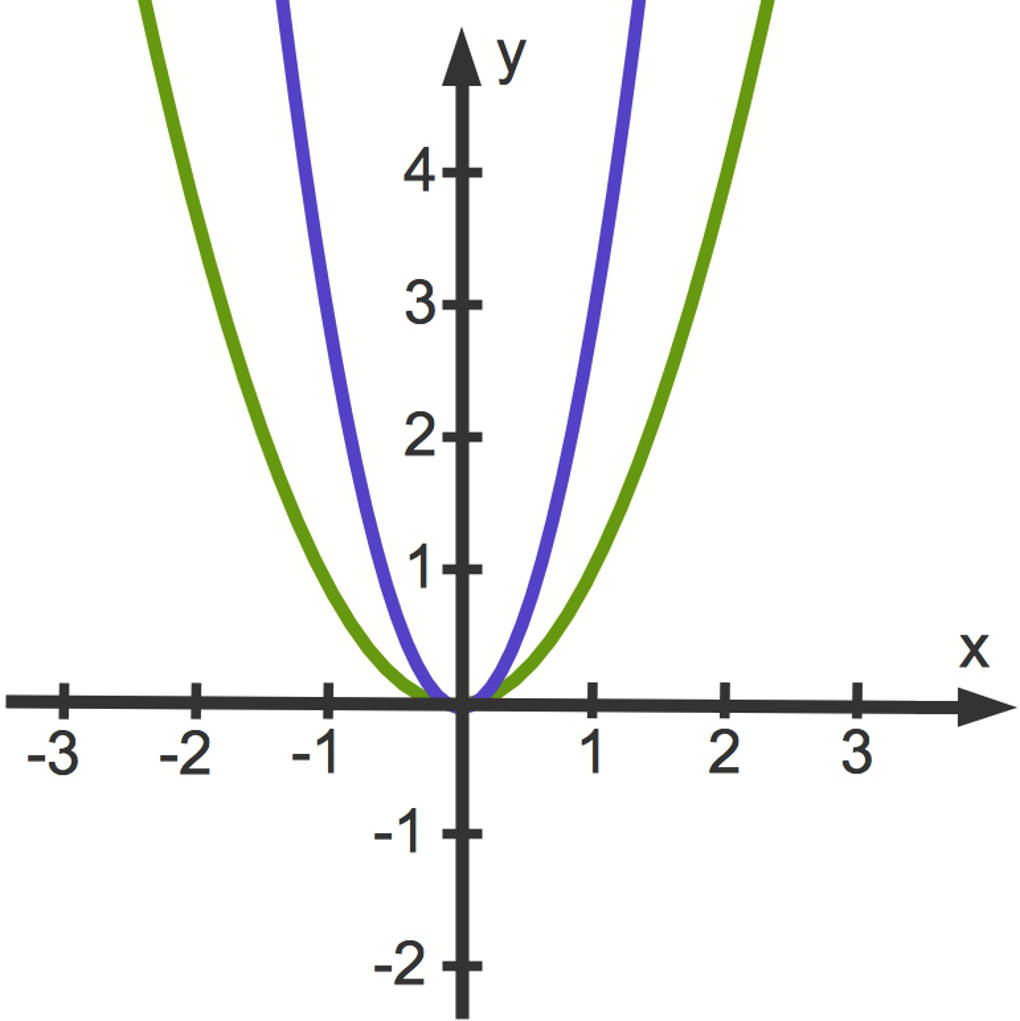
Was passiert, wenn $a$ negativ ist? Dann ist die Parabel nach unten geöffnet. Dies siehst du hier am Beispiel der Funktion $f(x)=-x^2$. Die zugehörige (violette) Parabel ist an der $x$-Achse gespiegelt.
Der Scheitelpunkt ist bei jeder der oben angegebenen Parabeln der Koordinatenursprung $S(0|0)$.
Parameter $e$
Der Parameter $e$ bewirkt eine Verschiebung entlang der $y$-Achse:
- nach oben für $e>0$ und
- nach unten für $e<0$.
Durch die Verschiebung ändert sich auch der Scheitelpunkt.
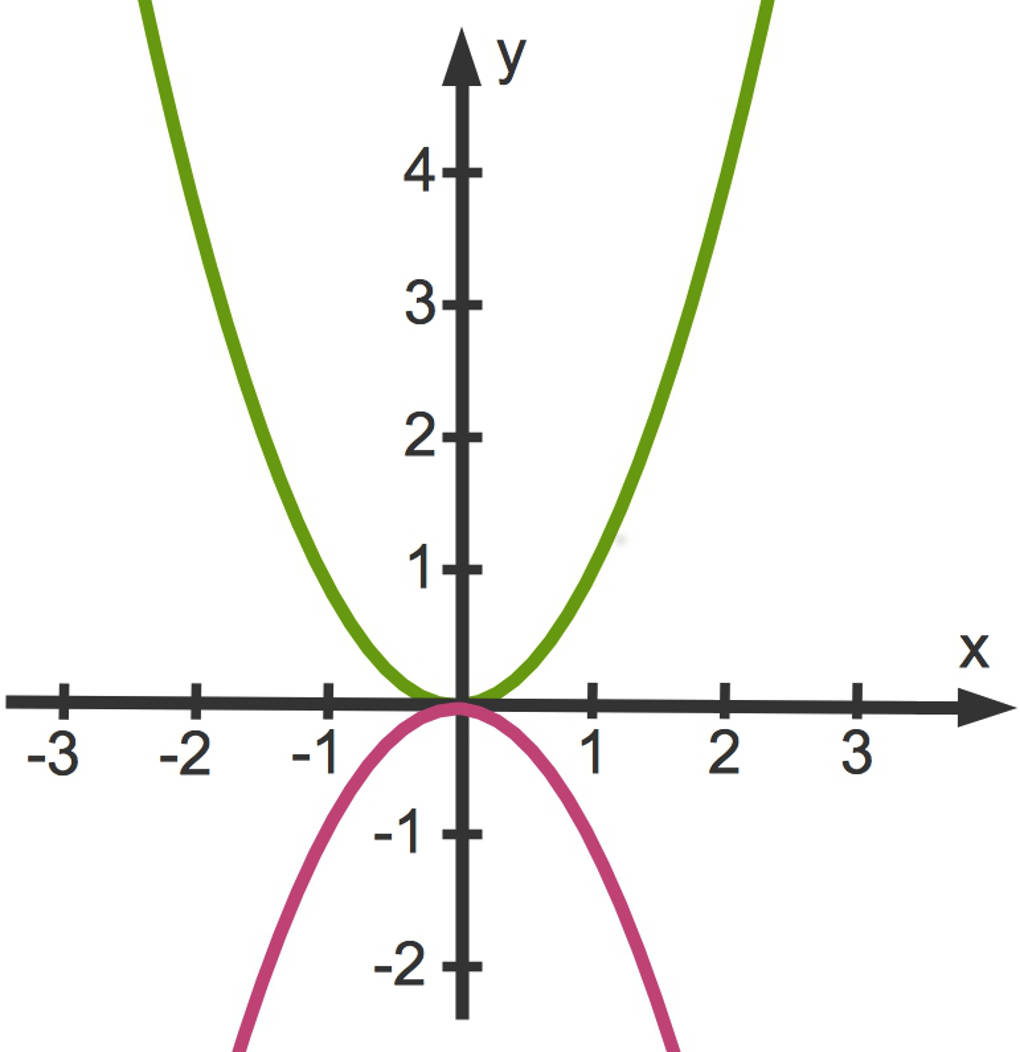
Hier siehst du die (orange) Parabel zu $f(x)=x^2+2$, welche um $2$ Längeneinheiten nach oben verschoben ist. Der Scheitelpunkt ist $S(0|2)$.
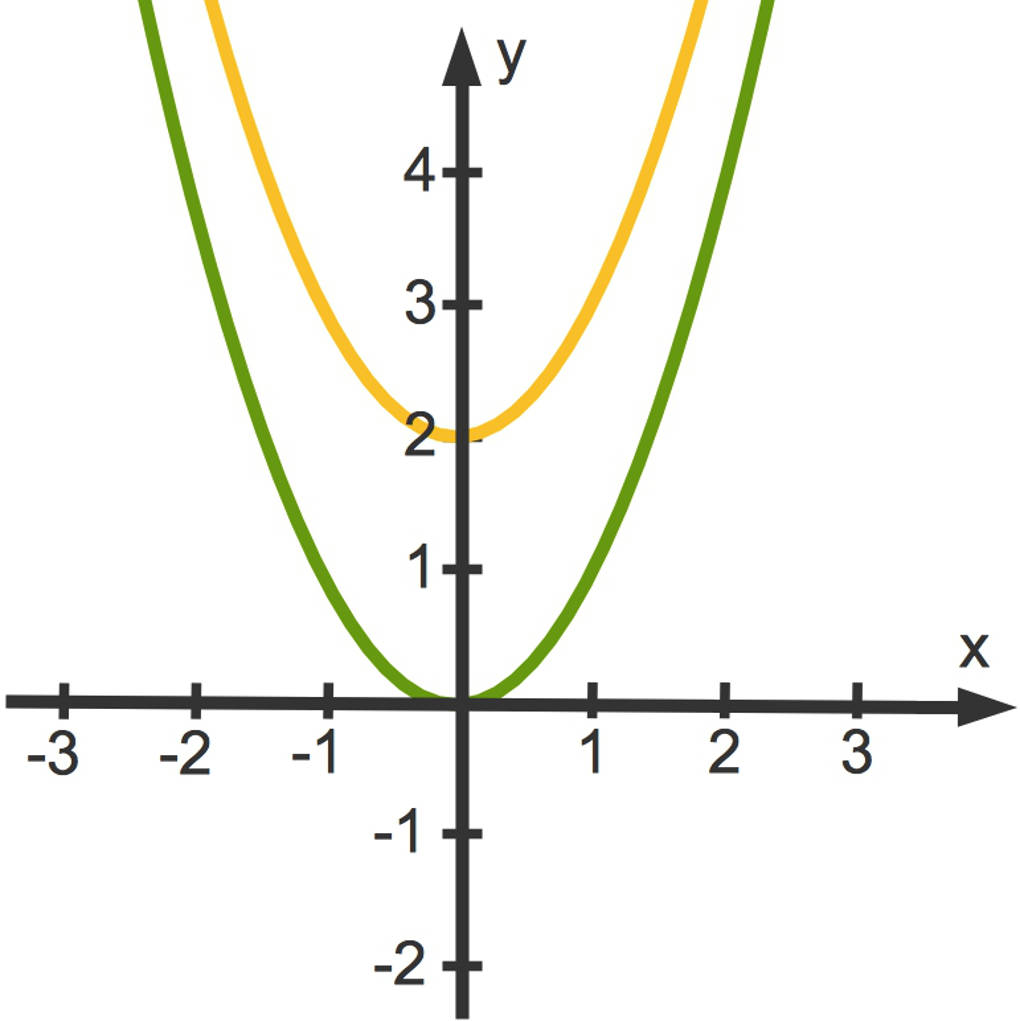
Die (hellblaue) Parabel gehört zu $f(x)=x^2-2$. Sie ist um $2$ Längeneinheiten nach unten verschoben. Der Scheitelpunkt ist $S(0|-2)$.
Parameter $d$
Der Parameter $d$ bewirkt eine Verschiebung entlang der $x$-Achse. Sei die Scheitelpunktform gegeben durch $f(x)=a(x-d)^2+e$, dann
- wird die Parabel nach rechts verschoben für $d>0$ und
- nach links für $d<0$.
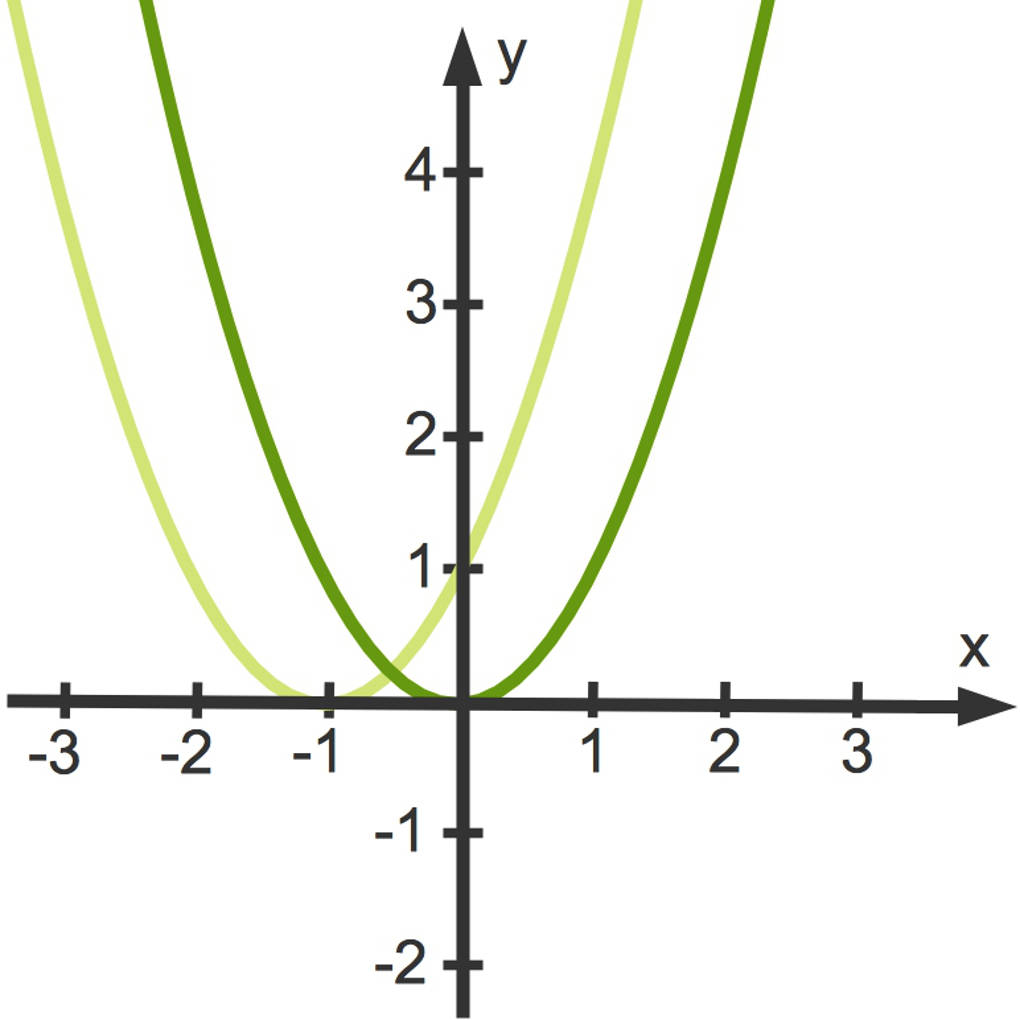
Beachte dabei das Minuszeichen! Die Parabel zu der Funktion $f(x)=(x-2)^2$ ist um $2$ Längeneinheiten nach rechts verschoben. Der Scheitelpunkt ist $S(2|0)$.
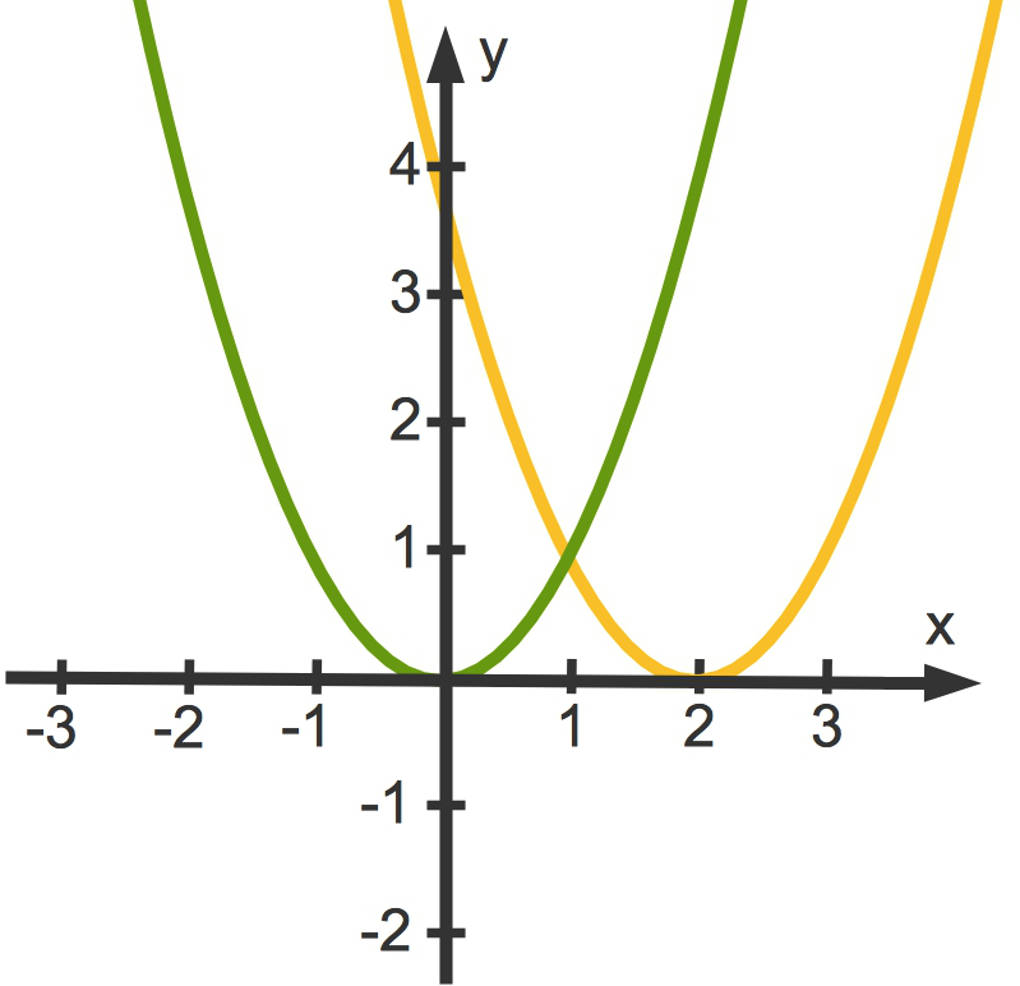
Die Parabel zu $f(x)=(x+1)^2$ ist dagegen um $1$ Längeneinheit nach links verschoben. Der Scheitelpunkt ist $S(-1|0)$.
Wie stellt man die Scheitelpunktform bei bekanntem Scheitelpunkt auf?
Wenn du den Scheitelpunkt einer Parabel sowie den Streckfaktor kennst, kannst du die zugehörige Scheitelpunktform aufschreiben.
Gegeben sei zum Beispiel der Scheitelpunkt $S(1|2)$ sowie $a=1$. Du setzt nun die Parameter $e=1$, $d=2$ und $a=1$ in folgende Scheitelpunktform ein:
$f(x)=a(x-d)^2+e$
Die Scheitelpunktform der Funktion lautet dann $f(x)=(x-1)^2+2$. Hier siehst du die zugehörige (hellblaue) Parabel.
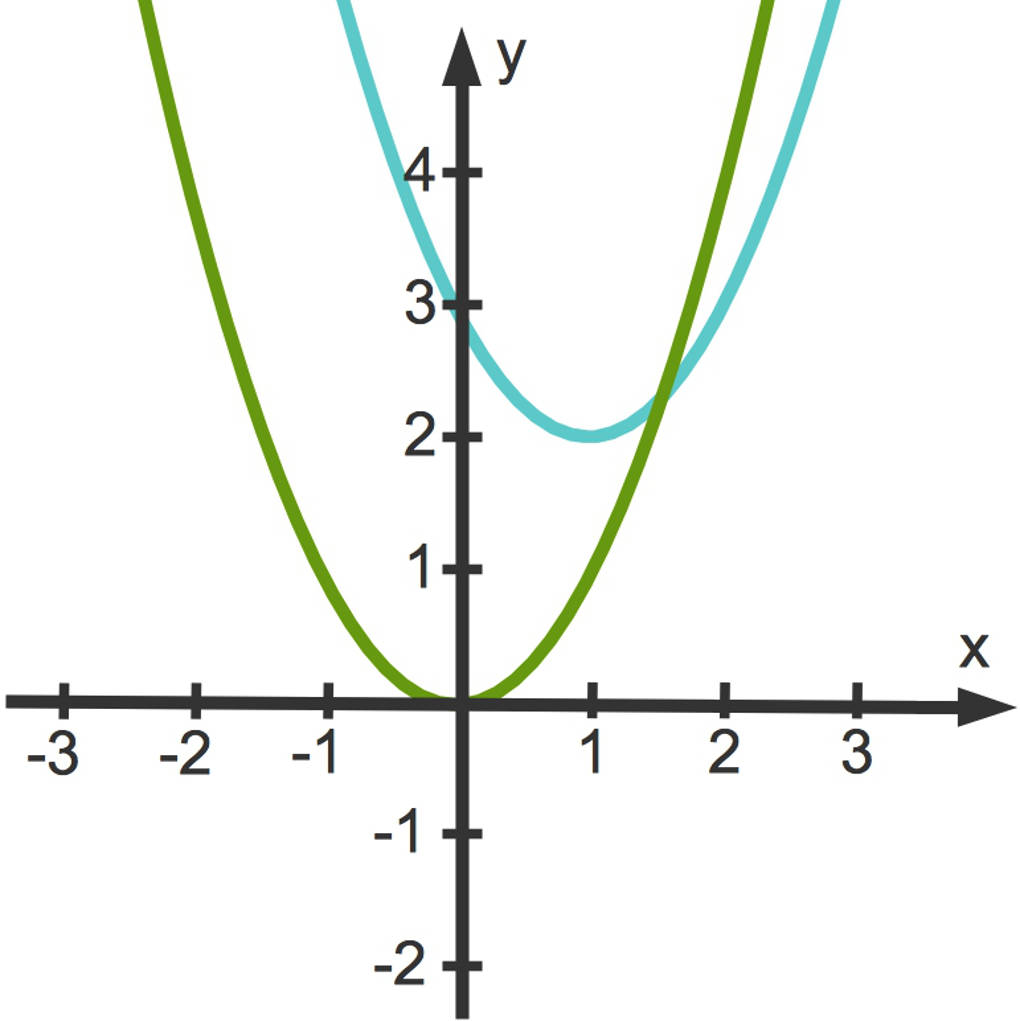
Du kannst an allen obigen Beispielen erkennen, dass du den Funktionsgraphen einer quadratischen Funktion in Scheitelpunktform schnell zeichnen kannst. Aber wie kannst du die Scheitelpunktform herleiten, wenn du die Funktion in einer anderen Form gegeben hast?
Wie stellt man die Scheitelpunktform ausgehend von der allgemeinen Form auf?
Du kannst, ausgehend von einer quadratischen Funktion in allgemeiner Form, eine Scheitelpunktform
- durch quadratische Ergänzung oder
- durch Ermitteln des Scheitelpunktes herleiten.
Quadratische Ergänzung
Betrachte das folgende Beispiel $f(x)=2x^2+8x+4$.
$\begin{array}{rcl}2x^2+8x+4&=&2(x^2+4x)+4\\&=&2(x^2+4x+4-4)+4\\&=&2((x+2)^2-4)+4\\&=&2(x+2)^2-4\end{array}$
Somit ist $f(x)=2(x+2)^2-4$.
Das ist genau die Scheitelpunktform dieser Funktion. Der Scheitelpunkt dieser Funktion ist $S(-2|-4)$. Hier siehst die zugehörige Parabel.
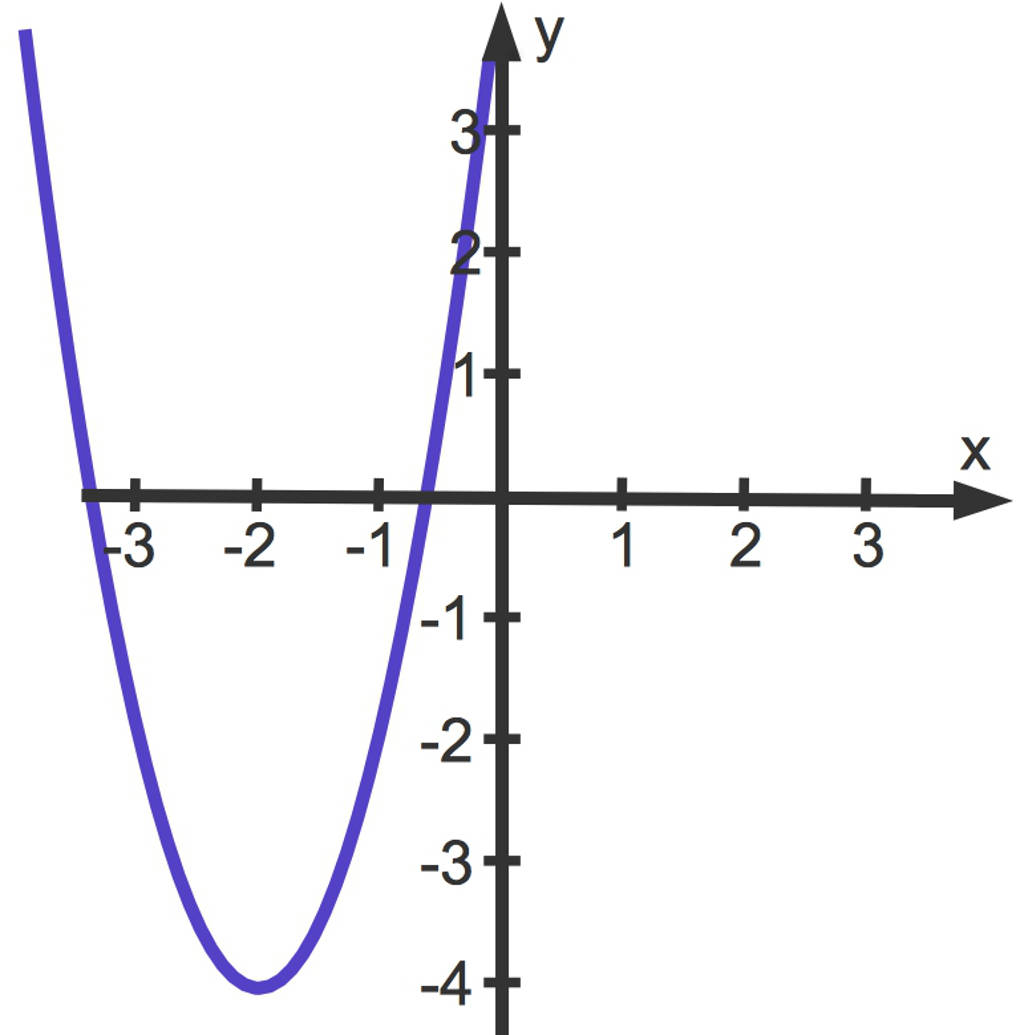
Ermitteln des Scheitelpunktes
Du kannst den Scheitelpunkt auch so bestimmen:
- Klammere $a$ aus.
- Die $x$-Koordinate des Scheitelpunktes ist die Hälfte des Faktors vor dem $x$ in der Klammer mit umgekehrtem Vorzeichen.
- Die $y$-Koordinate erhältst du durch Einsetzen der $x$-Koordinate in die Funktionsgleichung.
Dafür betrachten wir ein abschließendes Beispiel: $f(x)=3x^2-6x+9$.
- $3x^2-6x+9=3(x^2-2x+3)$
- Damit ist $d=-\frac{-2}2=1$ die $x$-Koordinate des Scheitelpunktes.
- Nun setzt du $1$ in die Funktionsgleichung ein: $e=f(1)=3\cdot 1^2-6\cdot 1+9=6$. Dies ist die $y$-Koordinate des Scheitelpunktes.
Der Scheitelpunkt ist also $S(1|6)$ und die Scheitelpunktform lautet $f(x)=3(x-1)^2+6$.
Wie überführt man die Scheitelpunktform in die allgemeine Form?
Ist eine quadratische Funktion in Scheitelpunktform gegeben, so kann sie in die allgemeine Form überführt werden. Betrachte hierzu die Funktion $f(x)=2(x+1)^2-4$
- Zunächst wird die erste oder zweite binomische Formel angewandt: $~f(x)=2(x^2+2x+1)-4$
- Dann wird die Klammer mit Hilfe des Distributivgesetzes aufgelöst, falls $a\neq 1$: $~f(x)=2x^2+4x+2-4$
- Abschließend werden alle gleichartigen Terme zusammengefasst: $~f(x)=2x^2+4x-2$
Alle Videos und Lerntexte zum Thema
Videos und Lerntexte zum Thema
Quadratische Funktionen: Scheitelpunkt und Scheitelpunktform (3 Videos, 1 Lerntext)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Quadratische Funktionen: Scheitelpunkt und Scheitelpunktform (4 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Winkelsummen in Dreiecken und Vierecken – Übungen







 Scheitelpunktform
Scheitelpunktform
 Umwandlung: Scheitelpunktform und allgemeine Form
Umwandlung: Scheitelpunktform und allgemeine Form
 Scheitelpunkt mithilfe der Nullstellen berechnen
Scheitelpunkt mithilfe der Nullstellen berechnen
 Quadratische Funktion – Parameter
Quadratische Funktion – Parameter









