Rationale Zahlen – Klammerregeln
Rationale Zahlen sind Brüche, die positiv oder negativ sein können. Erfahre, wie man den Betrag einer rationalen Zahl berechnet und die Klammerregeln bei rationalen Zahlen anwendet. Interessiert? Das und vieles mehr findest du im folgenden Text!


in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.

Grundlagen zum Thema Rationale Zahlen – Klammerregeln
Rationale Zahlen – Klammerregeln – Mathe
Heute lernst du, wie man das Assoziativgesetz und das Distributivgesetz auf die rationalen Zahlen anwenden kann. Anschließend lernst du die Klammerregeln bei rationalen Zahlen kennen. Zuerst schauen wir uns aber nun an, was rationale Zahlen sind.
Was sind rationale Zahlen – Definition
Rationale Zahlen sind positive und negative Zahlen, die sich als Bruch darstellen lassen. An der Zahlengerade gibt es den negativen Bereich, die Null und den positiven Bereich.
Auch die ganzen Zahlen sind in der Menge der rationalen Zahlen enthalten. Wir können an der Zahlengerade Brüche zwischen den ganzen Zahlen eintragen.
Der Betrag
Der Betrag einer rationalen Zahl ist ihr Abstand zur Null.
Beispiel: $|-3,5| = |3,5| = 3,5$
Aber wie rechnet man mit rationalen Zahlen in Klammern? Schauen wir uns auch dies gemeinsam an:
Das Assoziativgesetz der Addition für rationale Zahlen
Beim mehrfachen Addieren von rationalen Zahlen kann man Klammern beliebig setzen und weglassen.
Beispiel zum Assoziativgesetz der Addition
Im Folgenden schauen wir uns ein Beispiel zum Assoziativgesetz der Addition an:
$(6,5+3,3)+2,4 = 6,5+(3,3+2,4) = 6,5+3,3+2,4$
Egal ob wir erst die Klammer berechnen oder von links nach rechts addieren, wir erhalten in jedem Fall das Ergebnis $12,2$.
Anwendung des Assoziativgesetzes auf die Subtraktion
Da man jede Subtraktion auch als Addition schreiben kann, können wir das Assoziativgesetz auch auf die Subtraktion anwenden:
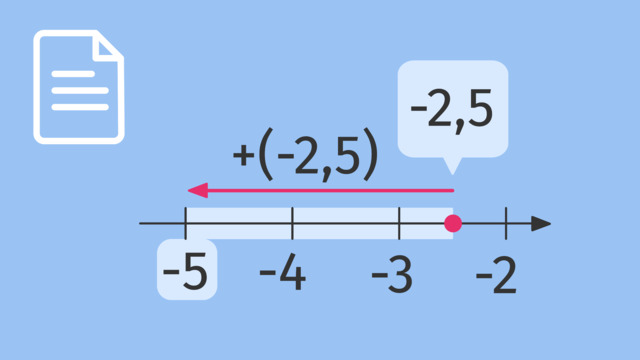
$6,5-(3,3+2,4) = 6,5 + (-3,3) + (-2,4)$
Klammergesetze
Allgemein gelten bei der Addition und Subtraktion rationaler Zahlen folgende Klammerregeln:
| Plusklammer | a+(b+c) = a+b+c |
| a+(b-c) = a+b-c | |
| Minusklammer | a-(b+c) = a-b-c |
| a-(b-c) = a-b+c |
Steht vor der Klammer ein Plus, so können wir die Klammer einfach auflösen. Steht vor der Klammer ein Minus, so müssen wir beim Auflösen der Klammer auf die Vorzeichen achten: Aus einem Minus in der Klammer wird dann ein Plus und aus einem Plus ein Minus.
Das Assoziativgesetz der Multiplikation
Das Assoziativgesetz gilt auch für die Multiplikation. Auch hier können wir beim Rechnen mit rationalen Zahlen Klammern beliebig setzen oder weglassen.
Beispiel zum Assoziativgesetz der Multiplikation
Nun schauen wir uns ein Beispiel zum Assoziativgesetz der Multiplikation an:
$(1,5 \cdot 1,5) \cdot 1,2 =1,5 \cdot (1,5 \cdot 1,2) = 1,5 \cdot 1,5 \cdot 1,2$
Bei allen drei Rechenausdrücken ist das Ergebnis $2,7$.
Wenn wir eine Division in eine Multiplikation umwandeln, können wir das Assoziativgesetz ebenso auf die Division anwenden.
Das Distributivgesetz für rationale Zahlen
Das Distributivgesetz lautet:
- $a \cdot (b+c) = a \cdot b + a\cdot c$
- $a \cdot (b-c) = a \cdot b - a\cdot c$
Beispiel zum Distributivgesetz für rationale Zahlen
Ein Beispiel für das Distributivgesetz sieht wie folgt aus:
$-2 \cdot (3,5+5,2)$
Hier steht in der Klammer eine Addition und außerhalb der Klammer eine Multiplikation. Berechnen wir zuerst die Klammer, so erhalten wir:
$-2 \cdot (3,5+5,2) = -2 \cdot 8,7 = -17,4$
Das Distributivgesetz besagt, dass wir auch zuerst die Zahlen in der Klammer jeweils mit dem Faktor multiplizieren und erst anschließend addieren können:
$-2 \cdot (3,5+5,2) = (-2) \cdot 3,5 + (-2) \cdot 5,2 = (-7) + (-10,4) = -17,4$
Beim Auflösen von Klammern mit rationalen Zahlen müssen wir darauf achten, die Vorzeichen nicht zu vergessen.
Wir können das Distributivgesetz auch nutzen, um Rechnungen zu vereinfachen:
$5,4 \cdot 7 = (5+0,4)\cdot 7 = 5 \cdot 7 + 0,4 \cdot 7 = 35 + 2,8 = 37,8$
In diesem Video zu Klammerregeln rationaler Zahlen …
… betrachten wir das Addieren und Subtrahieren rationaler Zahlen mit Klammern. Außerdem betrachten wir Klammergesetze für die Multiplikation und Division. Dabei wenden wir das Assoziativgesetz und das Distributivgesetz auf rationale Zahlen an verschiedenen Beispielen an.
Wenn du noch weitere Übungen zum Assoziativ- und Distributivgesetz von rationalen Zahlen suchst, so wirst du auf dieser Seite fündig. Hier findest du Aufgaben zum Rechnen mit Klammern mit rationalen Zahlen. Außerdem gibt es hier auch ein Arbeitsblatt zu Klammern bei rationalen Zahlen und zum Distributivgesetz für rationale Zahlen.
Transkript Rationale Zahlen – Klammerregeln
Das ist Peter Paket. Er ist Paketbote und wird jeden Tag vor eine neue Herausforderung gestellt. Wie das eine Mal als er sich auf das Dach verlaufen hat. Doch als er das Paket noch einmal näher betrachtete, ist ihm etwas wichtiges in Klammern aufgefallen. Und auch beim Rechnen mit rationalen Zahlen spielen Klammern eine große Rolle. Wiederholen wir dazu zunächst einmal, was rationale Zahlen überhaupt sind. Rationale Zahlen sind positive und negative Zahlen, die sich als Bruch darstellen lassen. Auch die ganzen Zahlen sind in der Menge der rationalen Zahlen enthalten. An der Zahlengeraden haben wir also den negativen Bereich, die Null und den positiven Bereich. Wir können Brüche zwischen den ganzen Zahlen eintragen. Der Betrag einer Zahl ist der Abstand dieser Zahl zur 0. So ist der Betrag von -3,5 gleich dem Betrag von 3,5 und das ist gleich 3,5. Schauen wir uns zunächst das Assoziativgesetz an. Für die Addition besagt es, dass man beim mehrfachen Addieren Klammern beliebig setzen, umsetzen oder auch weglassen kann. So ist in Klammern (6,5 + 3,3) + 2,4 dasselbe wie 6,5 + in Klammern (3,3+ 2,4) oder auch 6,5+3,3+2,4. Berechnen wir die erste Summe und rechnen zuerst die Klammern und addieren dann 2,4, so erhalten wir 12,2. Dasselbe Ergebnis erhalten wir , wenn wir zunächst 3,3+2,4 rechnen und dann 6,5 addieren und ebenso wenn wir von links nach rechts rechnen. Da man jede Subtraktion auch als Addition schreiben kann, können wir das Assoziativgesetz nun auf die Subtraktion anwenden. 6,5 minus in Klammern 3,3+2,4 ist also das gleiche wie 6,5 plus minus 3,3 plus minus 2,4. Allgemein gelten bei der Addition und Subtraktion folgende Klammergesetze: a + in Klammern b + c ist gleich a + b +c. Haben wir innerhalb der Klammer ein Minus, aber vor der Klammer ein +, so können wir die Klammern auch einfach so auflösen. a - in Klammern b + c ist gleich a - b - c. Ist innerhalb der Klammer ein Minus, so wird dies beim Auflösen der Klammern zu einem plus. Wenn sich ein Minus vor der Klammer befindet, müssen wir alle Plus-Zeichen in der Klammer zu einem Minus Zeichen umwandeln und umgekehrt, wenn wir die Klammer auflösen wollen. Das Assoziativgesetz gilt ebenso für die Multiplikation. Auch bei der Multiplikation können wir Klammern beliebig setzen oder weglassen. Rechnen wir alle drei Terme aus so sehen wir, dass sich bei jedem Term am Ende das Ergebnis 2,7 ergibt. Wenn wir eine Division in eine Multiplikation umwandeln, können wir das Assoziativgesetz ebenso für die Division anwenden. Machen wir weiter mit dem Distributivgesetz und schauen uns dazu dieses Beispiel an: Minus 2 mal in Klammern 3,5 + 5,2. Hier hast du also innerhalb der Klammer eine Addition und außerhalb der Klammer eine Multiplikation. Berechnen wir die Klammern zuerst, so erhalten wir Minus 2 mal 8,7 und das sind Minus 17,4. Das Distributivgesetz besagt nun, dass wir zunächst die Zahlen in der Klammer mit dem Faktor Minus 2 multiplizieren können. Wichtig ist, dass wir die Vorzeichen nicht vergessen! Nachdem wir dann die Produkte ausgerechnet haben, addieren wir und erhalten als Endergebnis also ebenfalls Minus 17,4. Andersherum kann man die Rechnung mithilfe des Distributivgesetzes vereinfachen und dann leichter im Kopf lösen. So können wir 5,4 mal 7 umschreiben zu in Klammern (5 +0,4) mal 7. Wir rechnen dann 5 mal 7 und 0,4 mal 7 und erhalten so das Endergebnis 37,8. Fassen wir zusammen. a + in Klammern b + c ist gleich a + b +c und a plus in Klammern b - c ist gleich a + b - c. a - in Klammern b + c ist gleich a minus b minus c und a - in Klammern b - c ist gleich a - b + c. Das Distributivgesetz besagt folgendes: r. Eine Summe bzw. Differenz wird mit einem Faktor multipliziert, indem man jeden Summanden bzw. Minuenden und Subtrahend einzeln mit diesem Faktor multipliziert... und die Produkte dann addiert bzw. subtrahiert. Andersherum kann man das Rechnen mithilfe des Distributivgesetzes wie im Beispiel vereinfachen und dann leichter im Kopf rechnen. Und Peter hat es mal wieder geschafft sein Paket zuzustellen.
Rationale Zahlen – Klammerregeln Übung
-
Gib das Assoziativ- und Distributivgesetz an.
TippsDas Assoziativgesetz der Addition und Multiplikation besagt, dass sich das Ergebnis einer reinen Addition bzw. reinen Multiplikation nicht ändert, wenn man Klammern umsetzt oder weglässt.
Sieh dir folgendes Beispiel an: $~ 2\cdot (3+5)$
Du kannst diese Aufgabe lösen, indem du entweder zuerst den Ausdruck in der Klammer berechnest und dann von links nach rechts weiter rechnest oder das Distributivgesetz anwendest:
- $2\cdot 8=16$
- $2\cdot 3+2\cdot 5=6+10=16$
LösungAssoziativgesetz der Addition
Das Assoziativgesetz der Addition besagt, dass sich das Ergebnis einer reinen Addition nicht ändert, wenn man Klammern umsetzt oder weglässt. Es gilt demnach:
- $a+(b+c)=(a+b)+c=a+b+c$
Betrachtest du eine Additions- bzw. Subtraktionsaufgabe, die eine Minusklammer enthält, so gehst du wie folgt vor: Alle Zeichen in der Klammer drehen sich um, die Klammer und das Minuszeichen davor fallen weg. Beachte hierbei, dass vor dem $b$ am Anfang der Klammer eigentlich ein Pluszeichen steht, das wir in der Regel nur aus „Faulheit“ nicht aufschreiben! Es gilt also:
- $a-(b+c)=a+(-b)+(-c)=a-b-c$
Das Assoziativgesetz der Multiplikation besagt, dass sich das Ergebnis einer reinen Multiplikation nicht ändert, wenn man Klammern umsetzt oder weglässt – also genauso wie für die Addition, nur mit Malpunkten statt Pluszeichen. Es gilt demnach:
- $a\cdot (b\cdot c)=(a\cdot b)\cdot c=a\cdot b\cdot c$
Das Distributivgesetz besagt, dass man statt eine Summe mit einer Zahl zu multiplizieren, auch jeden Summanden mit dieser Zahl multiplizieren und dann die Produkte addieren kann.
- $a\cdot (b+c)=ab+ac$
-
Vervollständige die Gleichungen mithilfe des Assoziativ- und Distributivgesetzes.
TippsHast du in deinem Term eine Minusklammer, so kannst du die Klammer weglassen, indem du alle Pluszeichen innerhalb der Klammer in Minuszeichen und alle Minuszeichen in Pluszeichen umwandelst.
Das Distributivgesetz lautet:
$a\cdot (b+c)=ab+ac$
LösungDas Assoziativ- und Distributivgesetz können manchmal das Rechnen deutlich vereinfachen. Sie lauten wie folgt:
Assoziativgesetz der Addition
- $a+(b+c)=(a+b)+c=a+b+c$
- $a-(b+c)=a+(-b)+(-c)=a-b-c$
- $a\cdot (b\cdot c)=(a\cdot b)\cdot c=a\cdot b\cdot c$
- $a\cdot (b+c)=ab+ac$
Nun wenden wir diese Gesetze auf die hier betrachteten Terme an und erhalten:
- $(6,5+3,3)+2,4=6,5+(3,3+2,4)$
- $6,5-(3,3+2,4)=6,5+(-3,3)+(-2,4)$
- $(1,5\cdot 1,5)\cdot 1,2=1,5\cdot (1,5\cdot 1,2)$
- $-2\cdot (3,5+5,2)=-2\cdot 3,5+(-2)\cdot 5,2$
-
Ordne den Aufgaben das jeweils angewandte Rechengesetz zu.
TippsDas Assoziativgesetz der Addition besagt, dass sich das Ergebnis einer reinen Addition nicht ändert, wenn man Klammern umsetzt oder weglässt. Es gilt demnach:
- $a+(b+c)=(a+b)+c=a+b+c$
- $a\cdot (b\cdot c)=(a\cdot b)\cdot c=a\cdot b\cdot c$
Das Distributivgesetz besagt, dass wir, anstatt eine Summe mit einer Zahl zu multiplizieren, auch jeden Summanden mit dieser Zahl multiplizieren und dann die Produkte addieren können.
LösungLass uns gemeinsam untersuchen, welche Gesetze in welchen Beispielen angewandt wurden.
1. Beispiel: $\quad 2\cdot (5\cdot 3)=(2\cdot 5)\cdot 3=10\cdot 3=30$
Nach dem ersten Gleichheitszeichen wird hier das Assoziativgesetz der Multiplikation genutzt: Anstatt zuerst das Produkt $5\cdot 3$ zu bestimmen, wird die Klammer so gesetzt, dass zuerst das Produkt $2\cdot 5$ berechnet wird, welches im nächsten Schritt dann mit dem Faktor $3$ multipliziert wird.
2. Beispiel: $\quad 2\cdot (5+3)=2\cdot 5+2\cdot 3=10+6=16$
Hier wird im ersten Schritt das Distributivgesetz angewandt. Dieses besagt, dass wir, anstatt eine Summe mit einer Zahl zu multiplizieren, auch jeden Summanden mit dieser Zahl multiplizieren und dann die Produkte addieren können. Genauso wird hier vorgegangen.
3. Beispiel: $\quad (5-3)\cdot 2=5\cdot 2-3\cdot 2=10-6=4$
Auch hier wird im ersten Schritt das Distributivgesetz angewandt, selbst wenn in der Klammer eine Differenz steht. Diese kannst du nämlich ebenfalls als Summe $2+(-3)$ schreiben.
4. Beispiel: $\quad 2+(5+3)=(2+5)+3=7+3=10$
Nach dem ersten Gleichheitszeichen wird hier das Assoziativgesetz der Addition genutzt: Anstatt zuerst die Summe $5+3$ zu bestimmen, wird die Klammer so gesetzt, dass zuerst die Summe $2+5$ berechnet wird, welche im nächsten Schritt zum Summanden $3$ addiert wird.
5. Beispiel: $\quad 5\cdot (2+3)=5\cdot 2+5\cdot 3=10 + 15=25$
Hier wird gleichfalls das Distributivgesetz genutzt.
6. Beispiel: $\quad (3\cdot 5)\cdot 5=3\cdot (5\cdot 5)=3\cdot 25=75$
Mit dem Assoziativgesetz der Multiplikation wird hier zuerst $5\cdot 5$ statt $3\cdot 5$ gerechnet.
-
Wende das Distributivgesetz an, um einfacher zu rechnen.
TippsZerlege den Faktor, der ein Dezimalbruch ist, in zwei Summanden (oder Minuenden und Subtrahenden), sodass die Multiplikation einfacher wird.
Sieh dir folgendes Beispiel an:
$6\cdot 7,6=6\cdot (7+0,6)=42+3,6=45,6$
LösungWir können das Distributivgesetz auch umgekehrt nutzen, um uns das Lösen einer Multiplikationsaufgabe zu erleichtern. Dazu zerlegen wir einen der Faktoren so, dass wir die Aufgabe mit geringerem Rechenaufwand lösen können. Wir erhalten dann folgende Rechnungen:
1. Beispiel
- $5,7\cdot 4=(5+0,7)\cdot 4=20+2,8=22,8$
2. Beispiel
- $6,9\cdot 5=(7-0,1)\cdot 5=35-0,5=34,5$
3. Beispiel
- $9\cdot 4,3=9\cdot (4+0,3)=36+2,7=38,7$
-
Gib die rationalen Zahlen der markierten Punkte auf der Zahlengeraden an.
Tipps$\frac 12$ liegt genau in der Mitte von $0$ und $1$. Ist diese Mitte markiert?
Alle Zahlen auf der Zahlengeraden, die links von der Null liegen, sind negativ.
LösungEine Zahlengerade dient zur Veranschaulichung von Zahlen als Punkte auf einer Geraden. Die Zahl $0$ teilt die Zahlengerade in zwei Teile. Auf der rechten Seite der $0$ befinden sich die positiven Zahlen, auf der linken Seite die negativen.
Der Bereich zwischen zwei aufeinanderfolgenden ganzen Zahlen kann unterschiedlich in gleich große Teile unterteilt werden. Teilen wir diesen Abstand zum Beispiel in drei gleich große Teile, entspricht jedes Teil einem Drittel. Genauso können wir ein Ganzes auch halbieren, sodass jedes Teil genau $\frac 12$ groß ist. Teilen wir das Ganze in $10$ gleich große Teile, zählt jedes Teil $\frac 1{10}=0,1$. Damit erhalten wir die hier abgebildeten Zahlen für die Zahlengerade.
-
Ermittle die Lösungen der jeweiligen Aufgaben.
TippsDu kannst hier entweder die Rechengesetze Assoziativ- und Distributivgesetz anwenden oder in folgender Reihenfolge vorgehen:
- Zuerst die Klammern berechnen, dabei beginnst du bei den inneren Klammern.
- Dann die Punktrechnungen vor den Strichrechnungen durchführen.
Sieh dir folgendes Beispiel an:
$\begin{array}{lll} 20-32-(1,8+3\cdot(1,3+3,7))\cdot 1,9 &=& 20-32-(1,8+3\cdot 5)\cdot 1,9 \\ &=& 20-32-(1,8+15)\cdot 1,9 \\ &=& 20-32-16,8\cdot 1,9 \\ &=& 20-32-31,92 \\ &=& -12-31,92 \\ &=& -43,92 \end{array}$
LösungWir können hier entweder die Rechengesetze Assoziativ- und Distributivgesetz anwenden oder in folgender Reihenfolge vorgehen:
- Zuerst die Klammern berechnen, dabei beginnen wir bei den inneren Klammern.
- Dann die Punktrechnungen vor den Strichrechnungen durchführen.
1. Beispiel
Zuerst wenden wir die Regel für Minusklammern an. Dann nutzen wir das Distributivgesetz, um uns die Multiplikation $5,4\cdot 9$ zu erleichtern. Wir zerlegen dazu den Faktor $5,4$ in die Summanden $5$ und $0,4$.
$\begin{array}{lll} 5,4\cdot 9+22,4-(4,5-2,5) &=& 5,4\cdot 9+22,4-4,5+2,5 \\ &=& (5+0,4)\cdot 9+22,4-4,5+2,5 \\ &=& 45+3,6+22,4-4,5+2,5 \\ &=& 69 \end{array}$
2. Beispiel
Hier nutzen wir im ersten Schritt das Distributivgesetz. Danach berechnen wir den Klammerausdruck und rechnen anschließend von links nach rechts:
$\begin{array}{lll} (5-2,2)\cdot 5+(6+33,8) &=& 25-11+(6+33,8) \\ &=& 25-11+39,8 \\ &=& 53,8 \end{array}$
3. Beispiel
Im ersten Schritt formulieren wir die Summe in der ersten Klammer so um, dass wir Summanden erhalten, mit denen wir einfacher rechnen können, und wenden dann das Distributivgesetz an. Bevor wir erneut das Distributivgesetz anwenden formulieren wird die Summe wieder geschickt um. Dann heben wir die hintere Minusklammer auf, indem wir alle Plus- und Minuszeichen in der Klammer entsprechend umkehren:
$\begin{array}{lll} 2\cdot (1,6+3,3)\cdot 3-(1,2-6) &=& 2\cdot (0,9+4)\cdot 3-(1,2-6) \\ &=& (1,8+8)\cdot 3-(1,2-6) \\ &=& (0,8+9)\cdot 3-(1,2-6) \\ &=& 2,4+27-(1,2-6) \\ &=& 2,4+27-1,2+6 \\ &=& 34,2 \end{array}$
4. Beispiel
Hier nutzen wir weder Assoziativ- noch Distributivgesetz. Wir berechnen beginnend bei der innersten Klammer zuerst die Klammerausdrücke, dabei beachten wir Punkt- vor Strichrechnung:
$\begin{array}{lll} 54-(2+3\cdot(3,6+2,4))\cdot 1,2 &=& 54-(2+3\cdot 6)\cdot 1,2 \\ &=& 54-(2+18)\cdot 1,2 \\ &=& 54-20\cdot 1,2 \\ &=& 54-24 \\ &=& 30 \end{array}$
9.728
sofaheld-Level
6.600
vorgefertigte
Vokabeln
8.284
Lernvideos
38.567
Übungen
33.604
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Klassenstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung


 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?
















Taff Taff
hat schon alle meine lehrer ersetzt
Peter der Paket Bote ist einfach Boss
Cooles Video ☺☻♥
NICE 🥵😏