Negative Zahlen – Anordnung und Betrag
in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
5 Minuten verstehen
5 Minuten üben
2 Minuten Fragen stellen
Bereit für eine echte Prüfung?
Grundlagen zum Thema Negative Zahlen – Anordnung und Betrag
Nach dem Schauen dieses Videos wirst du in der Lage sein, negative Zahlen an der Zahlengerade abzulesen, die Gegenzahl einer Zahl zu bestimmen und den Betrag einer Zahl zu berechnen.
Zunächst lernst du, die wie du zwei Zahlen an der Zahlengerade vergleichst. Anschließend lernst du die Begriffe Gegenzahl und Betrag und ihre Bedeutung kennen. Abschließend lernst du, wie du verschiedene Zahlen auf der Zahlengerade ihrer Größe nach einsortieren kannst.
Das Video beinhaltet Schlüsselbegriffe, Bezeichnungen und Fachbegriffe wie negative Zahlen, Zahlenstrahl, Zahlengerade, Gegenzahl und Betrag.
Bevor du dieses Video schaust, solltest du bereits wissen, was ganze Zahlen und was rationale Zahlen sind.
Transkript Negative Zahlen – Anordnung und Betrag
Zugvogel müsste man sein. Den Winter im warmen Süden verbringen und die Sonne genießen!
Bei angenehmen Temperaturen um die zweiundzwanzig Grad lässt es sich doch leben!
Daheim im kalten Norden ist das Wetter jetzt grau und trüb!
Und außerdem um ganze fünfundzwanzig Grad kälter!
Wie kalt es dort genau ist?
Um das sagen zu können, müssen wir mit „negativen Zahlen“ rechnen.
Das Thermometer zeigt für die Zugvögel im Süden also zweiundzwanzig Grad an.
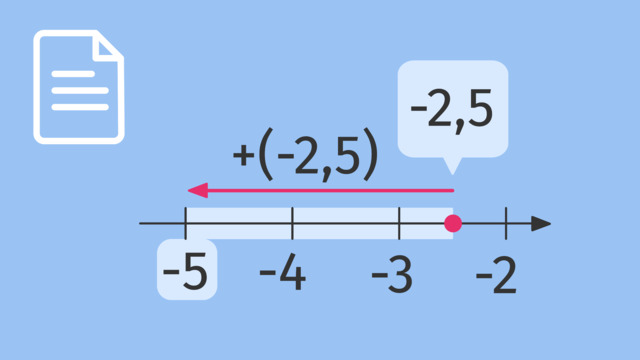
Um jetzt auch die Temperatur im kalten Deutschland anzuzeigen, müssen wir von zweiundzwanzig fünfundzwanzig abziehen.
Bei dieser Differenz ist der Minuend zweiundzwanzig allerdings kleiner als der Subtrahend fünfundzwanzig.
Wir unterschreiten also den Nullpunkt und erhalten minus drei.
Minus drei Grad, ganz schön frostig!
Negative Zahlen können wir uns an der Zahlengerade veranschaulichen.
Dafür nehmen wir zum Abschnitt der positiven Zahlen, also den Zahlen größer Null, den Abschnitt der negativen Zahlen hinzu.
Diese werden mit einem Minus als Vorzeichen gekennzeichnet.
Das Plus als Vorzeichen von positiven Zahlen wird fast immer weggelassen.
Die Pfeilspitze unserer Zahlengerade gibt an, dass die dort eingetragenen Zahlen von links nach rechts immer größer werden.
Je weiter rechts eine Zahl liegt, umso größer ist sie.
Das heißt: Wenn wir die Größe von zwei Zahlen vergleichen möchten, können wir überlegen, welche Zahl auf der Zahlengerade weiter rechts liegt.
Diese ist dann die größere der beiden Zahlen.
So ist zum Beispiel minus vier kleiner als drei.
Und wenn wir die Zahlen minus 2,5 und minus 4,75 vergleichen, erkennen wir, dass minus 4,75 die kleinere der beiden Zahlen ist.
So weit, so gut.
Wenn wir uns mit negativen Zahlen beschäftigen, haben wir es oft mit den Begriffen „Gegenzahl“ und „Betrag“ zu tun.
Was diese Begriffe bedeuten, schauen wir uns jetzt mal genauer an.
Jede Zahl auf der Zahlengerade hat genau eine Gegenzahl.
Zahl und Gegenzahl unterscheiden sich dabei nur durch ihre Vorzeichen.
So ist zum Beispiel die Gegenzahl der Fünf die minus Fünf.
Die Gegenzahl von minus 2,7 ist plus 2,7.
Fällt dir etwas auf?
Genau! Zahl und Gegenzahl liegen jeweils symmetrisch zur Null.
Sie haben also beide den gleichen Abstand zur Null.
Hier kommt der zweite Begriff ins Spiel: der Betrag.
Der Betrag einer Zahl gibt immer an, wie groß der Abstand einer Zahl zur Null ist.
Dieser Abstand ist bei Zahl und Gegenzahl gleich groß.
Sowohl die fünf, als auch die minus fünf haben einen Abstand von fünf Längeneinheiten zur Null.
Für den Betrag ist also die Länge des Abstands zur Null und nicht das Vorzeichen der Zahl entscheidend.
Wir notieren den Betrag, indem wir einen senkrechten Strich vor, und einen senkrechten Strich hinter die betrachtete Zahl setzen.
Das sind die sogenannten Betragsstriche.
Da Abstände immer positiv sind, ist auch der Betrag einer Zahl immer positiv.
Wenn wir also von einer negativen Zahl den Betrag berechnen, ist dieser trotzdem positiv.
Dazu noch ein paar Beispiele:
Der Betrag von vier ist gleich vier, da die vier, vier Längeneinheiten von der Null entfernt ist.
Die Gegenzahl minus vier liegt auf der Zahlengerade auf der anderen Seite der null.
Der Abstand ist aber auch hier gleich vier, und somit ist auch der Betrag von minus vier gleich vier.
Und welche Zahlen haben den Betrag 2,1?
Das ist einmal die Zahl minus 2,1, aber auch ihre Gegenzahl 2,1.
Zum Abschluss eine kleine Übungsaufgabe:
Diese Zahlen sollen ihrer Größe nach geordnet werden.
Wie würdest du vorgehen?
Zunächst sollten wir die Beträge von minus 4,8, und 2,5 bestimmen.
Dann können wir die entsprechenden Zahlen in der Zahlengerade einsortieren, und sie somit der Größe nach ordnen.
Die Winterferien sind vorbei. Jetzt müssen auch die Zugvögel zurück in den kalten Norden.
Sie haben gehört, dass die Temperatur dort bei dem Betrag von minus neun Grad liegt!
Na klasse, da können sie sich ja warm anziehen.
Während sich die Zugvögel auf dem Weg befinden, fassen wir nochmal kurz zusammen.
Die negativen Zahlen liegen auf der Zahlengerade links von der Null.
Wir können die Größe von zwei Zahlen vergleichen, indem wir untersuchen, welche Zahl weiter rechts auf der Zahlengerade liegt.
Diese ist dann die größere der beiden Zahlen.
Außerdem können wir nun den Betrag von Zahlen berechnen.
Dieser gibt den Abstand der jeweiligen Zahl zur Null an, und ist somit immer positiv.
Zwei Zahlen, die den gleichen Betrag, also den gleichen Abstand zur Null haben, werden außerdem Zahl und Gegenzahl genannt.
Na dann können wir uns jetzt wohl Experten für negative Zahlen nennen!
Und die Zugvögel? Die haben gerade wohl nicht so gut aufgepasst. Ganz so kalt ist es dann doch nicht!
Negative Zahlen – Anordnung und Betrag Übung
-
Vervollständige den Text zu negativen Zahlen und Gegenzahl.
TippsJe weiter rechts eine Zahl auf der Zahlengerade liegt, desto größer ist sie.
Die Gegenzahl von $+6$ ist $-6$.
LösungNegative Zahlen kennen wir bereits aus dem Alltag. Beispielsweise ist es bei einer Außentemperatur von $-3^{\circ}\text{C}$ ziemlich kalt.
Negative Zahlen können an der Zahlengerade veranschaulicht werden. Zu dem Abschnitt der bereits bekannten positiven Zahlen kommt der Abschnitt der negativen Zahlen hinzu.
Diese stehen links von $0$ und werden mit einem Minus als Vorzeichen gekennzeichnet, zum Beispiel $-8$. Positive Zahlen hingegen haben ein positives Vorzeichen, welches man aber meistens einfach weglässt. Beispielsweise schreibt man $2,5$ statt $+2,5$.
An der Zahlengerade gilt: Je weiter links eine Zahl liegt, desto kleiner ist sie. Somit ist zum Beispiel $-4 \lt -3$.Jede Zahl hat eine Gegenzahl. Zahl und Gegenzahl unterscheiden sich nur durch ihr Vorzeichen. Zahl und Gegenzahl liegen jeweils symmetrisch zur Null. Die Gegenzahl der $5$ ist die Zahl $-5$.
-
Gib die Zahlen der Größe nach geordnet an.
TippsDer Betrag einer Zahl gibt ihren Abstand zur Null an.
Beispiel:
$\vert-2,3\vert = 2,3$
Je weiter rechts eine Zahl auf der Zahlengeraden liegt, desto größer ist sie.
LösungUm die Zahlen zu sortieren, können wir uns überlegen, an welcher Position der Zahlengeraden sie liegen. Denn es gilt: Je weiter rechts eine Zahl liegt, desto größer ist sie.
Dazu betrachten wir zuerst die Beträge. Der Betrag einer Zahl gibt ihren Abstand zur Null an. Daher ist er immer positiv. Es gilt:
$\vert2,5\vert = 2,5$
$\vert-4,8\vert = 4,8$Wir müssen also die folgenden Zahlen sortieren:
- $-3,5$
- $4,2$
- $4,8$
- $2,5$
Die negative Zahl $-3,5$ ist am kleinsten. Sie steht ganz links.
Die $2,5$ steht an zweiter Stelle. Außerdem gilt:$4,2 \lt 4,8$
Es ergibt sich somit folgende Reihenfolge:
$-3,5 \lt \vert2,5\vert \lt 4,2 \lt \vert-4,8\vert$
-
Vergleiche die Zahlen.
Tipps- $\vert-3\vert = 3$
- $\vert2,7\vert = 2,7$
- $\vert+12\vert = 12$
- $\vert-4,5\vert = 4,5$
Je weiter rechts eine Zahl auf der Zahlengeraden liegt, desto größer ist sie.
LösungUm die Zahlen zu vergleichen, können wir uns überlegen, an welcher Position der Zahlengeraden sie liegen. Denn es gilt: Je weiter rechts eine Zahl liegt, desto größer ist sie.
Außerdem müssen wir beachten, dass der Betrag einer Zahl immer positiv ist. Damit ergibt sich:Beispiel 1:
$-6,25$ liegt weiter rechts als $-6,5$, also:
$-6,25 \gt -6,5$
Beispiel 2:
$\vert-3,2\vert = 3,2$
$3,2$ liegt weiter rechts als $-3,1$, also:
$-3,1 \lt \vert-3,2\vert$
Beispiel 3:
$\vert-22,2\vert = 22,2$, also:
$\vert-22,2\vert = 22,2$
Beispiel 4:
$-12,12$ liegt weiter rechts als $-12,21$, also:
$-12,12 \gt -12,21$
Beispiel 5:
$\vert-13,4\vert = 13,4$
$\vert13\vert = 13$
$13,4$ liegt weiter rechts als $13$, also:
$\vert-13,4\vert \gt \vert13\vert$
-
Ordne gleiche Zahlen einander zu.
TippsZahl und Gegenzahl unterscheiden sich nur durch ihr Vorzeichen.
Achte auf die Reihenfolge:
- Bei der Gegenzahl von $\vert 3 \vert$ musst du zunächst den Betrag bilden, dann die Gegenzahl.
- Bei $\vert$Gegenzahl von $3 \vert$ musst du erst die Gegenzahl bilden und dann den Betrag.
Beispiel:
Die Gegenzahl von $\vert-4,5\vert$ ist die Gegenzahl von $4,5$ und diese ist $-4,5$.
LösungUm die Zahlen zuordnen zu können, müssen wir wissen, was der Betrag einer Zahl und was die Gegenzahl einer Zahl ist:
Der Betrag einer Zahl ist ihr Abstand zur Null. Er ist immer positiv.
Wir schreiben die Zahl dann in Betragstriche: $\vert-3,4\vert$.Die Gegenzahl einer Zahl ist die Zahl, welche das entgegengesetzte Vorzeichen hat.
Somit ergibt sich:
- $\vert -24 \vert$ ist $24$.
- Die Gegenzahl von $24$ ist $-24$.
- $-2,4$ ist die Gegenzahl von $2,4$.
- Der Betrag von $-2,4$ ist $\vert-2,4\vert$.
- Die Gegenzahl von $\vert-1,24\vert$ ist gleich der Gegenzahl von $1,24$. Dies ist gleich $-1,24$.
- $\vert$Gegenzahl von $-1,24\vert$ ist $\vert1,24\vert = 1,24$.
-
Bestimme die markierten Zahlen.
TippsAchte auf das Vorzeichen der Zahlen: Die Zahlen, welche links von der Null liegen, sind negative Zahlen. Sie haben als Vorzeichen ein Minuszeichen wie $-4$.
Die Zahl $-2,5$ liegt zwischen der $-2$ und der $-3$.
Die Zahl $5,5$ liegt zwischen der $5$ und der $6$.
LösungNegative Zahlen können an der Zahlengeraden veranschaulicht werden. Dazu wird zum Abschnitt der positiven Zahlen der Abschnitt der negativen Zahlen hinzugenommen.
Wir unterscheiden in unserem Beispiel also zunächst einmal zwischen negativen Zahlen, welche links von $0$ liegen, und positiven Zahlen, welche rechts von $0$ liegen.
Die Zahl $-4,5$ ist negativ und liegt in der Mitte zwischen der $-4$ und der $-5$. Die Zahl $-1,5$ liegt genau zwischen der $-1$ und der $-2$. Auch die Zahl $-3$ ist negativ und liegt links von $0$.
Die Zahl $2,2$ ist eine positive Zahl. Sie liegt zwischen der $2$ und der $3$, nahe bei der $2$. Und die Zahl $3,9$ liegt zwischen der $3$ und der $4$, nahe der $4$.
-
Ordne die Zahlen der Größe nach.
TippsJe weiter links eine Zahl auf der Zahlengeraden liegt, desto kleiner ist sie.
Der Betrag einer Zahl ist ihr Abstand zur Null. Er ist immer positiv. Wir schreiben die Zahl dann in Betragstriche: $\vert-3,4\vert$.
Die Gegenzahl einer Zahl ist die Zahl, welche das entgegengesetzte Vorzeichen hat.
LösungUm die Zahlen zu sortieren, können wir uns überlegen, an welcher Position der Zahlengeraden sie liegen. Denn es gilt: Je weiter rechts eine Zahl liegt, desto größer ist sie.
Dazu betrachten wir zuerst den Betrag. Dabei gilt:
$\vert3,1\vert = 3,1$
Wir betrachten nun die Gegenzahlen. Dabei gilt:
Gegenzahl von $21,3 = -21,3$
Gegenzahl von $-4 = 4$Wir müssen also folgende Zahlen sortieren:
- $4$
- $-21,3$
- $3,1$
- $-20,3$
- $-3,2$
- $4,2$
Die negativen Zahlen liegen generell weiter links als die positiven Zahlen. $-21,3$ ist die kleinste Zahl, da sie am weitesten links liegt. Außerdem ist $-20,3 \lt -3,2$. Bei den positiven Zahlen ist die Reihenfolge $3,1 \lt 4 \lt 4,2$. Insgesamt ergibt sich also:
Gegenzahl von $21,3 \lt -20,3 \lt -3,2 \lt \vert3,1\vert \lt$ Gegenzahl von $-4 \lt 4,2$
8.905
sofaheld-Level
6.601
vorgefertigte
Vokabeln
7.695
Lernvideos
37.343
Übungen
33.674
Arbeitsblätter
24h
Hilfe von Lehrkräften
Inhalte für alle Fächer und Klassenstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebeziehungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Quadrat
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Was Ist Eine Viertelstunde
- Prisma
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Satz Des Pythagoras
- Dreieck Grundschule
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Zahlen In Worten Schreiben
- Meter
- Orthogonalität
- Schriftlich Multiplizieren
- Brüche gleichnamig machen
- Brüche Multiplizieren
- Potenzgesetze
- Distributivgesetz
- Bruchgleichungen lösen – Übungen
- Flächeninhalt Dreieck
- Rationale Zahlen
- Volumen Berechnen
Einfach toll erklärt
Habe es verstanden 🫡😁😁😁
Ihr seid die besten
Sofatuzor ist sehr gut
Hallo Betül, vielen Dank für deine Frage. In der Aufgabe wird der Betrag von -4,8 betrachtet. Da der Betrag immer positiv ist und den Abstand zur Null misst, gilt |-4,8| = 4,8. Daher ist die Zahl hier positiv. Ich hoffe, das hilft dir so weiter. Liebe Grüße aus der Redaktion!
Wie kann die -4,8 bei den positiven Bereich sein ?? Oder hab ich da was falsch gesehen
Gut erklärt aber ich habe ein Fehler entdeckt: da steht -4,8 und nicht 4,8 ( können sie es bitte erklären)