Lineare Gleichungssysteme
durch Probieren lösen, ax + by = c, Koeffizienten, Geradengleichungen
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Lineare Gleichungen
- Gleichungen mit einer Variablen
- Gleichungen mit zwei Variablen
- Koordinatenform
- Lineare Funktionsgleichung
Lineare Gleichungen
Gleichungen mit einer Variablen
Gleichungen mit einer Variablen hast du sicherlich schon einmal gesehen. Ein Beispiel wäre $2x+4=12$.
Dies ist eine Gleichung mit einer Variable. Du löst diese Gleichung durch Umkehroperationen:
$\begin{array}{rclll} 2x+4&=&12&|&-4\\ 2x&=&8&|&:2\\ x&=&4 \end{array}$
Gleichungen mit zwei Variablen
Eine Gleichung kann auch zwei Variablen haben: $4x-2y=12$ liegt in Koordinatenform vor. Wenn du diese Gleichung äquivalent umformst, erhältst du in der letzten Zeile eine lineare Funktionsgleichung:
$\begin{array}{rclll} 4x-2y&=&12&|&+2y\\ 4x&=&12+2y&|&-12\\ 4x-12&=&2y&|&:2\\ 2x-6&=&y \end{array}$
Alle Paare $(x|y)$, die diese Gleichung lösen, bilden die Lösungsmenge. Bei linearen Funktionen ist dies eine Gerade.
Wie kannst du diese Gerade zeichnen? Hier gibt es zwei Möglichkeiten, je nachdem, ob die Gleichung in Koordinatenform oder als Funktionsgleichung vorliegt.
Koordinatenform
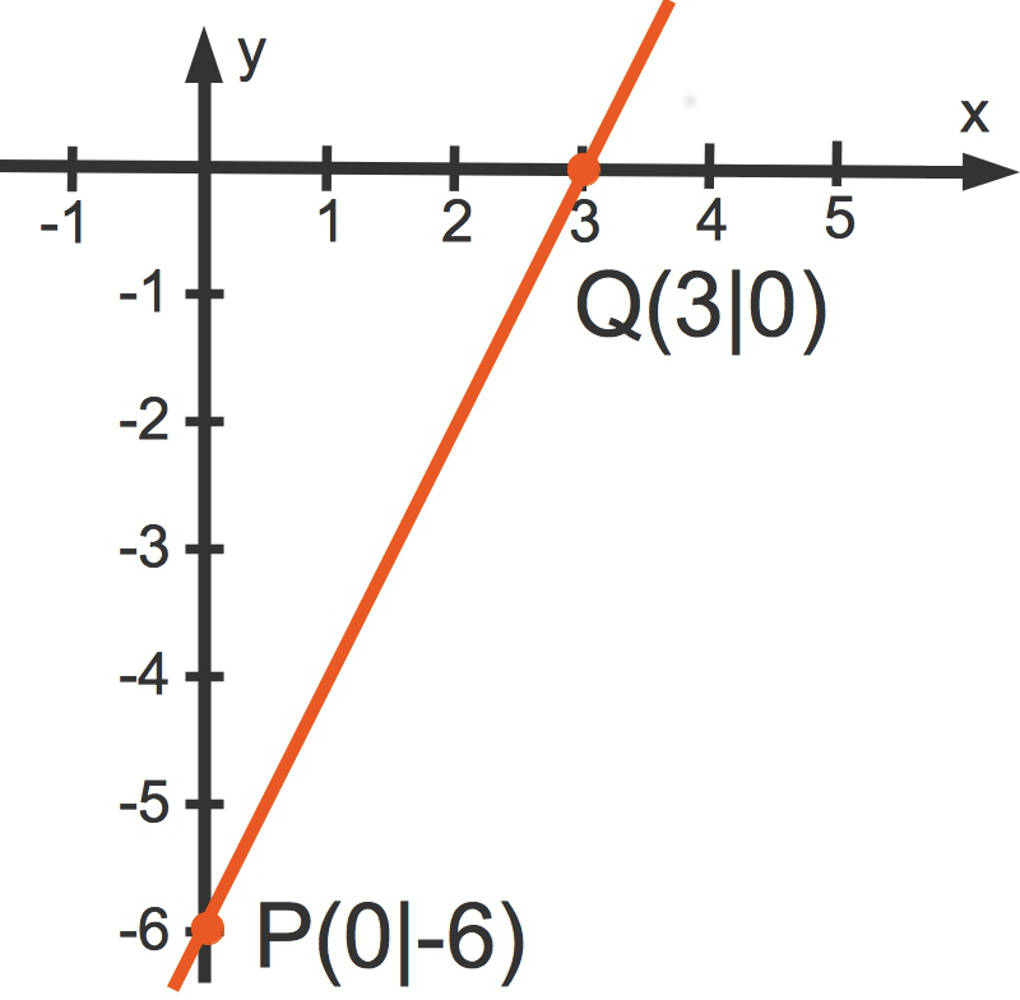
Wenn die Gleichung in Koordinatenform $4x-2y=12$ vorliegt, kannst du die Achsenschnittpunkte leicht berechnen. Dazu setzt du zuerst $x=0$ und danach $y=0$ in die Gleichung ein und berechnest die andere Koordinate.
- $x=0$ führt zu $-2y=12$. Wir dividieren nun durch $-2$ und erhalten $y=-6$. Der Punkt $P(0|-6)$ liegt auf der Geraden.
- $y=0$ führt zu $4x=12$. Wir dividieren nun durch $4$ und du erhältst $x=3$. Der Punkt $Q(3|0)$ liegt auf der Geraden.
Diese Achsenschnittpunkte zeichnest du in ein Koordinatensystem und verbindest sie zu einer Geraden.
Lineare Funktionsgleichung
Wenn die lineare Funktionsgleichung $y=2x-6$ gegeben ist, gehst du wie folgt vor:
- Du trägst zuerst den y-Achsenabschnitt ein. Dieser ist $y=-6$. In dem obigen Bild entspricht dies dem Punkt $P$.
- Von dort aus zeichnest du ein Steigungsdreieck. So gelangst du zu einem weiteren Punkt der Geraden.
- Nun verbindest du die Punkte miteinander und erhältst die gleiche Gerade wie bei der Koordinatenform.
Zwei Gleichungen mit zwei Variablen
Ein lineares Gleichungssystem mit zwei Variablen besteht aus zwei Gleichungen. In beiden Gleichungen kommen die Variablen $x$ und $y$ vor.
Hier siehst du ein lineares Gleichungssystem mit zwei Variablen in der Standardform:
$\begin{array}{llll} \text{I}& a \cdot x+b \cdot y &=& c\\ \text{II}& d \cdot x+e \cdot y &=& f \end{array}$
Die Faktoren $a$, $b$, $d$ und $e$ vor den Variablen werden als Koeffizienten bezeichnet. Wir verwenden $\text{I}$ und $\text{II}$, um die Gleichungen zu nummerieren.
Beide Gleichungen liegen in Koordinatenform vor. Du kannst also zu jeder Gleichung die zugehörige Gerade, auf welcher die Lösungspaare liegen, zeichnen. Es gibt die folgenden Lagemöglichkeiten:
- Die beiden Geraden sind identisch und es gibt unendlich viele Lösungen für das Gleichungssystem.
- Die beiden Geraden sind parallel und es gibt keine Lösung für das Gleichungssystem.
- Die beiden Geraden schneiden sich in einem Punkt und es gibt genau eine Lösung für das Gleichungssystem.
Das graphische Lösen von linearen Gleichungssystemen
Schauen wir uns das folgende Beispiel für das graphische Lösen von Gleichungssystemen an:
$\begin{array}{llll} \text{I} & x+2y & =& 4\\ \text{II} &-2x+y & = & -3 \end{array}$
Du kannst zu beiden Gleichungen die zugehörige Gerade zeichnen. Diese siehst du hier. Die rote Gerade gehört zu der oberen Gleichung, die grüne Gerade zu der unteren:
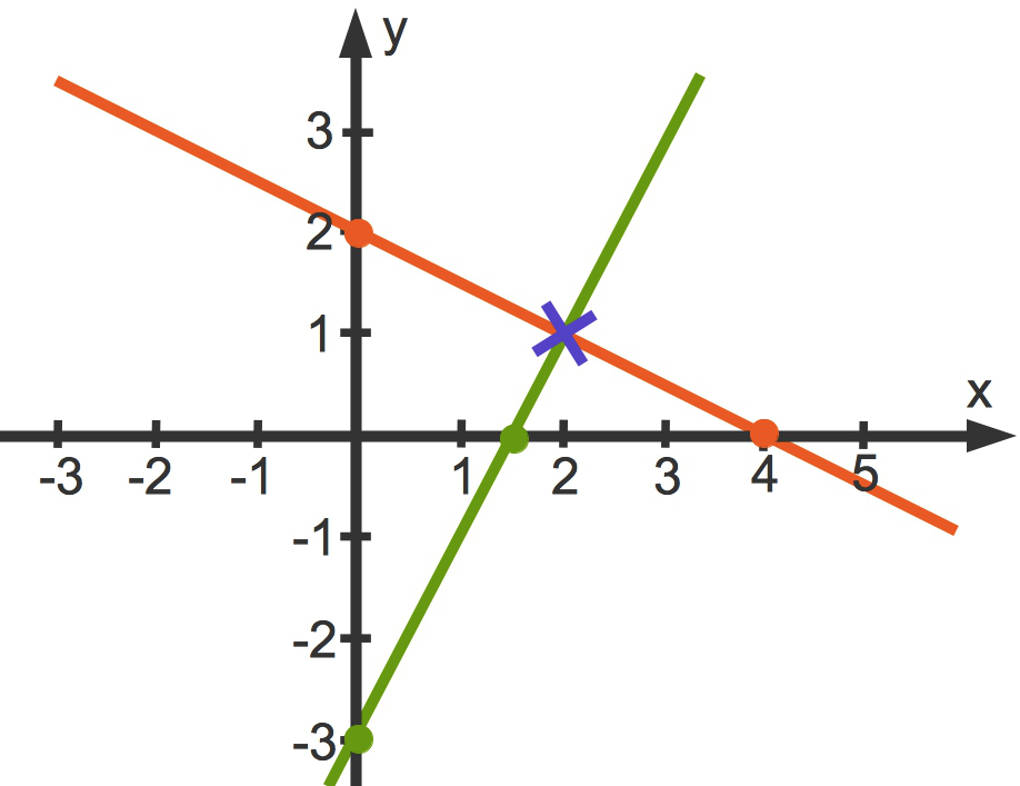
Die beiden Geraden schneiden sich. Das bedeutet, es gibt nur eine Lösung. Die Koordinaten des Schnittpunktes $S(2|1)$ entsprechen der Lösung des Gleichungssystems: $x=2$ und $y=1$.
Du kannst eine Probe durchführen:
$\begin{array}{llll} \text{I}& 2+2 \cdot 1 & = & 4 &\checkmark\\ \text{II}&-2 \cdot 2 +1 & = &-3 &\checkmark \end{array}$
Das rechnerische Lösen von linearen Gleichungssystemen
Im Folgenden lernst du verschiedene Lösungsverfahren für lineare Gleichungssysteme kennen. Unabhängig vom Verfahren erhalten wir für das Gleichungssystem die gleichen Lösungen.
Vielleicht gefällt dir eines der drei folgenden Verfahren besonders. Dann verwende immer dieses Verfahren.
Das Additionsverfahren
Wir wollen das Additionsverfahren einmal Schritt für Schritt für dieses Gleichungssystem durchführen:
$\begin{array}{llll} \text{I}&x + 2 y &=&4\\ \text{II}& -2 x + y &=& -3 \end{array}$
Zuerst multiplizieren wir eine oder beide Gleichungen mit einer Zahl ungleich $0$, so dass die Koeffizienten einer der beiden Variablen bis auf das Vorzeichen übereinstimmen. Die Vorzeichen sind also unterschiedlich. Wir multiplizieren die obere Gleichung mit $2$:
$\begin{array}{llll} \text{I}& 2x + 4 y &=& 8\\ \text{II}& -2 x + y &=& -3 \end{array}$
Dann addieren wir die beiden Gleichungen (daher Additionsverfahren): $\text{I}+\text{II}$. Dabei wird eine Variable eliminiert:
$\begin{array}{llll} \text{I+II:}& 2x-2x + 4 y +y &=& 8+(-3)\\ & 5y & = & 5\\ & y & = & 1 \end{array}$
Wir setzen $y=1$ in eine der beiden Ausgangsgleichungen ein. So erhalten wir die Lösung für die andere Variable. Wählen wir Gleichung $\text{I}$, führt dies zu:
$\text{I}~~~~~ x + 2 \cdot 1 =4 ~~~ \Leftrightarrow ~~~ x=2 $.
Das Lösungspaar ist $(2|1)$.
Das Einsetzungsverfahren
Werfen wir nun einen Blick auf das Einsetzungsverfahren und führen es ebenfalls Schritt für Schritt für dieses Gleichungssystem durch:
$\begin{array}{llll} \text{I}&x + 2 y &=& 4\\ \text{II}& -2 x + y &=& -3 \end{array}$
Im ersten Schritt formen wir eine der beiden Gleichungen nach einer der beiden Variablen um. Wählen wir Gleichung $\text{II}$ und formen nach $y$ um:
$\text{II}~~~~~ y = 2x-3$.
Wir setzen nun anstelle der Variablen $y$ den Term $2x-3$ in die andere Gleichung ein. So erhältst du eine Gleichung mit nur einer einzigen Variablen, die wir nach $x$ auflösen können:
$\begin{array}{llll} \text{II}& x + 2(2x-3)&=&4\\ & x + 4x - 6 & = & 4\\ & 5x-6 & = & 4\\ & 5x & = & 10\\ & x & = & 2 \end{array}$
Nun setzen wir $x=2$ noch in eine von beiden Gleichungen ein und erhalten $y=2\cdot 2-3=4-3=1$.
Auch hier lautet das Lösungspaar $(2|1)$.
Das Gleichsetzungsverfahren
Beim Gleichsetzungsverfahren setzen wir zwei Terme gleich. Dafür müssen wir allerdings ein paar Dinge beachten. Wählen wir wieder das Gleichungssystem:
$\begin{array}{llll} \text{I}&x + 2 y &=& 4\\ \text{II}& -2 x + y &=& -3 \end{array}$
Zuerst formen wir die Gleichungen (sofern notwendig) um, sodass auf jeweils einer Seite der beiden Gleichungen das Gleiche steht:
$\begin{array}{llllll} \text{I}&x + 2 y &=& 4 &~~~\Leftrightarrow~~~& 2y = -x+4\\ \text{II}& -2 x + y &=& -3 &~~~\Leftrightarrow~~~& 2y = 4x-6 \end{array}$
Wir können nun die beiden anderen Seiten gleichsetzen. So erhältst du eine Gleichung mit einer Variable. Für diese Variable $x$ lässt sich ein Wert ermitteln:
$\begin{array}{lll} -x+4 & = & 4x-6\\ x & = & 2 \end{array}$
Nun setzen wir die Lösung in eine der beiden Ausgangsgleichungen ein. Wählen wir die untere Gleichung:
$-2\cdot 2+y=-3 ~~~~~ \Leftrightarrow ~~~~~ y = 1$
Wie du siehst, führt auch dieses Verfahren zu der gleichen Lösung: $(2|1)$.
Alle Videos und Lerntexte zum Thema
Videos und Lerntexte zum Thema
Lineare Gleichungssysteme (8 Videos, 2 Lerntexte)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Lineare Gleichungssysteme (8 Arbeitsblätter)
-
 Lineare Gleichungssysteme mit zwei Variablen – Definition
PDF anzeigen
Lineare Gleichungssysteme mit zwei Variablen – Definition
PDF anzeigen -
 Lineare Gleichungssysteme zeichnerisch lösen – Überblick
PDF anzeigen
Lineare Gleichungssysteme zeichnerisch lösen – Überblick
PDF anzeigen -
 Gleichungssysteme graphisch lösen – Durchführung
PDF anzeigen
Gleichungssysteme graphisch lösen – Durchführung
PDF anzeigen -
 Additionsverfahren
PDF anzeigen
Additionsverfahren
PDF anzeigen -
 Additionsverfahren – Übungen
PDF anzeigen
Additionsverfahren – Übungen
PDF anzeigen -
 Einsetzungsverfahren
PDF anzeigen
Einsetzungsverfahren
PDF anzeigen -
 Einsetzungsverfahren – Übungen
PDF anzeigen
Einsetzungsverfahren – Übungen
PDF anzeigen -
 Gleichsetzungsverfahren
PDF anzeigen
Gleichsetzungsverfahren
PDF anzeigen
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung





















