Multiplikation: Halbschriftlich und schriftlich
Um große Zahlen auch ohne Taschenrechner multiplizieren zu können, verwendest du die schriftliche oder halbschriftliche Multiplikation.
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Was ist Multiplikation?
- Die schriftliche Multiplikation
- Die schriftliche Multiplikation mit Kommazahlen
- Die halbschriftliche Multiplikation
Was ist Multiplikation?
Die Multiplikation ist eine der vier Grundrechenarten. Multiplizieren ist ein anderer Ausdruck für Malnehmen. Merke dir für die Multiplikation: „Faktor mal Faktor gleich Produkt“. Auf die Reihenfolge kommt es beim Multiplizieren nicht an. Die Multiplikation ist nämlich kommutativ: Das bedeutet, dass die beiden Faktoren vertauschbar sind. Das Ergebnis verändert sich nicht. Deswegen heißen beide Größen, die multipliziert werden, auch gleich: Faktor.
Betrachten wir einige Beispiele:
- 365 $\cdot$ 24. Hier sind 365 und 24 die Faktoren.
- 82,40 $\cdot$ 23. Die Faktoren sind 82,40 und 23.
- 412 $\cdot$ 4. Dieses Mal sind die Faktoren 412 und 4.
Das Ergebnis einer Multiplikation wird als Produkt bezeichnet. Im Folgenden siehst du, wie du ein solches Produkt berechnen kannst.
Die schriftliche Multiplikation
Wir beginnen mit dem ersten Beispiel 365 $\cdot$ 24. Du weißt sicher schon, dass du dies auch so schreiben kannst 365 $\cdot$ (20 + 4). Wir multiplizieren also 365 zuerst mit 20 und dann mit 4 und addieren schließlich die beiden Ergebnisse. Dies führt zu der schriftlichen Multiplikation.
Dabei gehst du wie folgt vor: Du beginnst bei dem rechten Faktor 24 und multiplizierst die größte Stelle dieses Faktors (2) mit dem linken Faktor von rechts nach links.
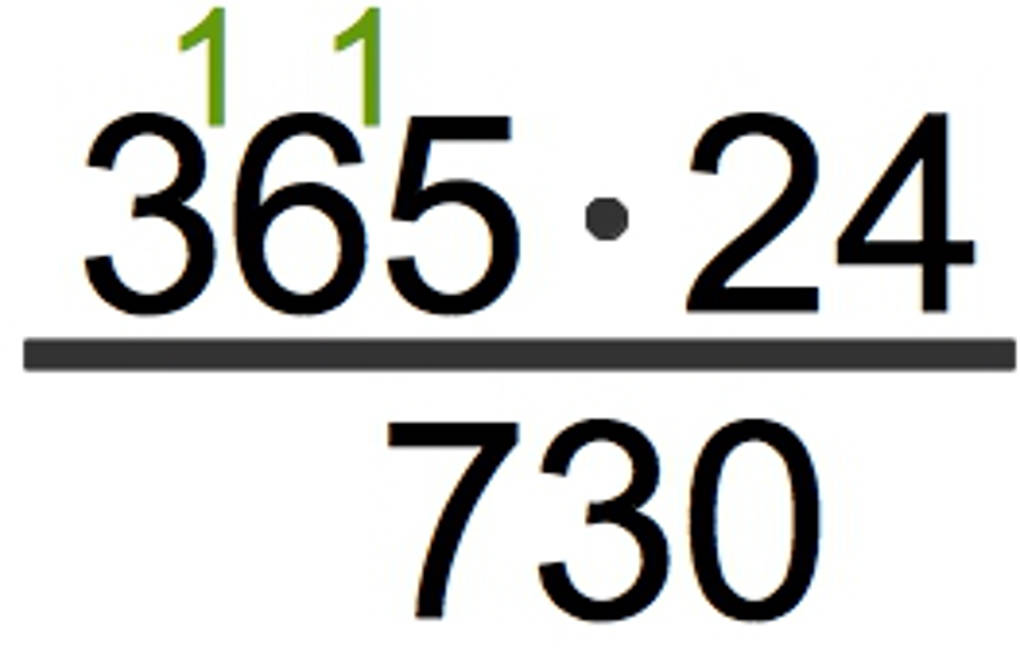
Machen wir dies einmal gemeinsam:
- 2 $\cdot$ 5 = 10. Du schreibst die 0 unter die größte Stelle des rechten Faktors. Die 1 schreibst du als Übertrag an die nächste Stelle des linken Faktors.
- 2 $\cdot$ 6 = 12. Nun addierst du den Übertrag 12 + 1 = 13. Du schreibst die 3 vor die bereits aufgeschriebene 0 und die 1 wieder als Übertrag an die nächste Stelle des linken Faktors.
- 2 $\cdot$ 3 = 6. Wieder addierst du den Übertrag zu 6 + 1 = 7. Diese 7 schreibst du vor die 30, die bereits da steht.
Ebenso multiplizierst du die kleinere Stelle des rechten Faktors mit dem linken Faktor.
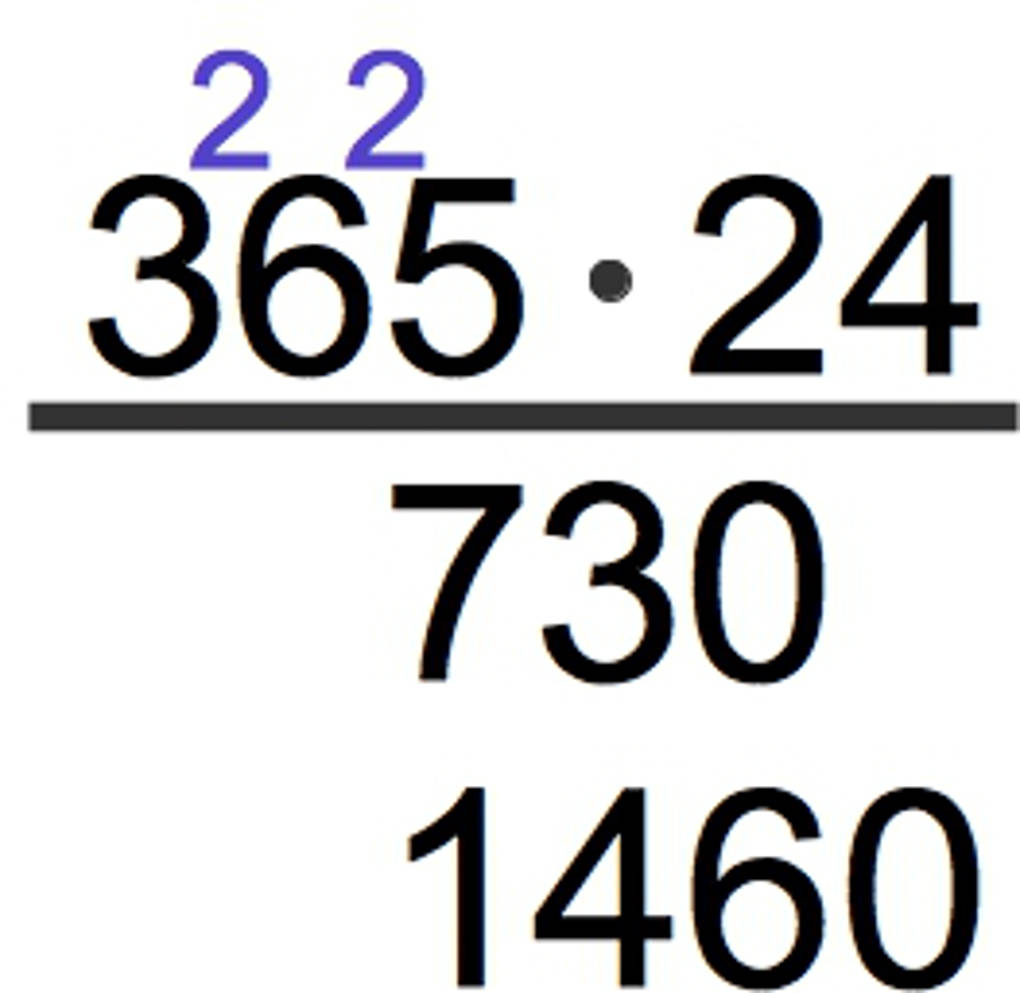
Die beiden Produkte addierst du zuletzt stellengenau und erhältst so das Ergebnis dieser Multiplikation 365 $\cdot$ 24 = 8760.
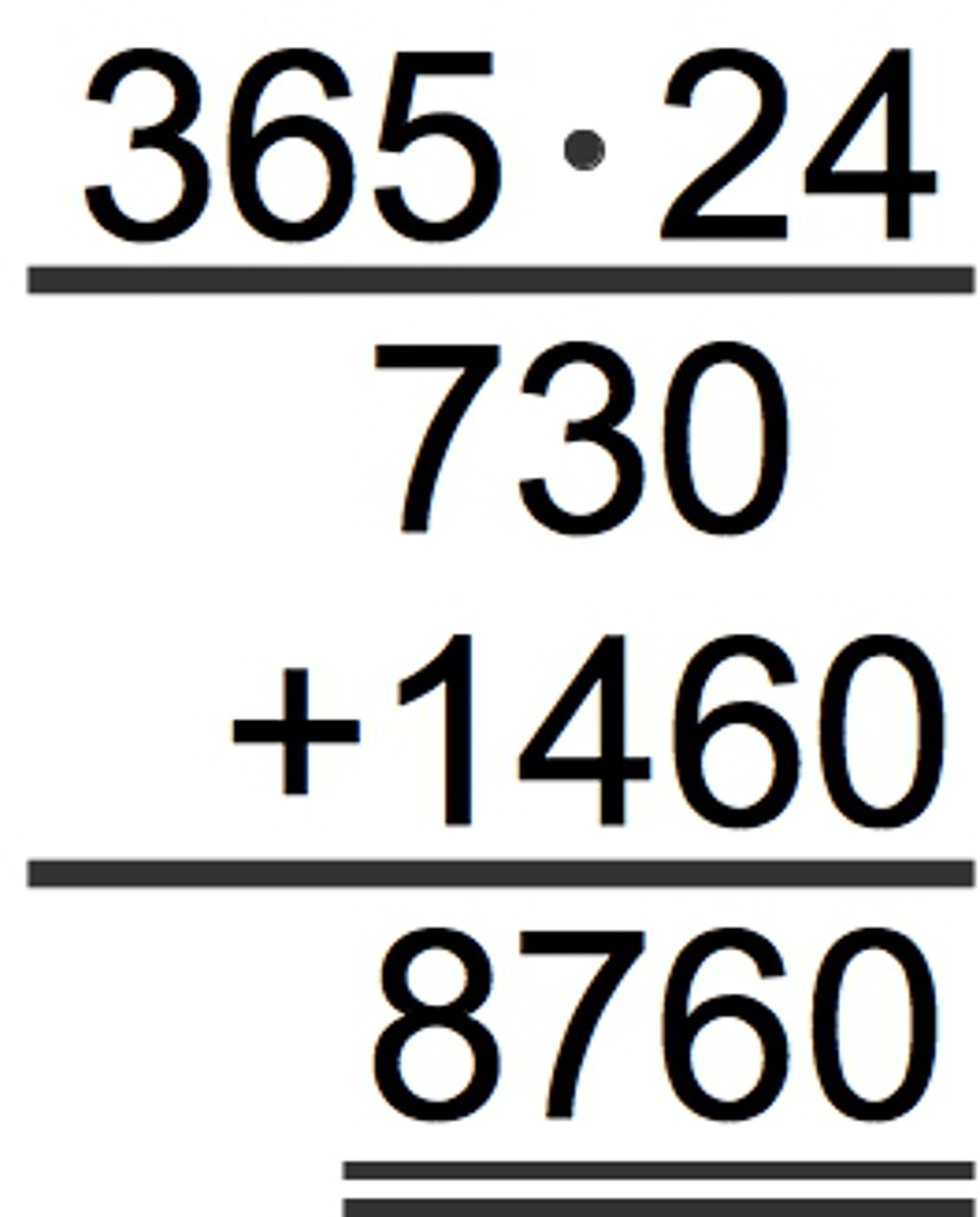
Die schriftliche Multiplikation mit Kommazahlen
Ebenso, wie du bei dem ersten Beispiel multipliziert hast, kannst du auch Kommazahlen schriftlich multiplizieren.
Nun berechnen wir das Ergebnis des zweiten Beispiels 82,40 $\cdot$ 23. Du gehst dabei genauso vor wie bei der schriftlichen Multiplikation ohne Kommazahlen. Du beachtest die Kommazahlen zunächst nicht:

Das Ergebnis hat ebenso viele Stellen nach dem Komma, wie die beiden Faktoren gemeinsam: Der linke Faktor hat zwei und der rechte Faktor keine Stellen nach dem Komma. Das sind zusammen zwei Stellen nach dem Komma. Nun kannst du das Komma setzen und das Produkt angeben: 82,40 $\cdot$ 23 = 1895,20.
Die halbschriftliche Multiplikation
Ähnlich wie beim halbschriftlichen Dividieren gehst du auch beim halbschriftlichen Multiplizieren vor.
Ein Beispiel bleibt noch: 412 $\cdot$ 4. Du multiplizierst erst einmal die Hunderter, dann die Zehner und letztlich die Einer des linken Faktors mit dem rechten Faktor. Zuletzt addierst du die einzelnen Produkte. Dies kannst du hier sehen:
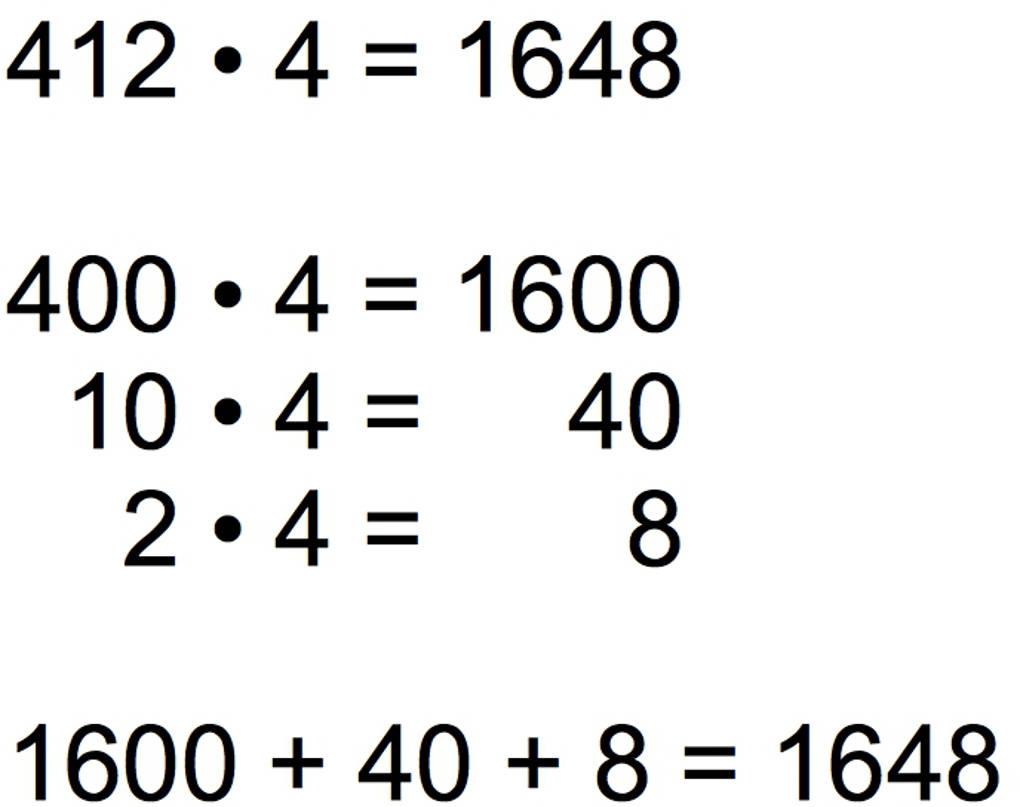
Das Produkt ist somit 412 $\cdot$ 4 = 1648.
Nun hast du viel gelernt und bist gut gerüstet für das Multiplizieren im Alltag.
Alle Videos zum Thema
Videos zum Thema
Multiplikation: Halbschriftlich und schriftlich (8 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Multiplikation: Halbschriftlich und schriftlich (8 Arbeitsblätter)
-
 Halbschriftliches Multiplizieren
PDF anzeigen
Halbschriftliches Multiplizieren
PDF anzeigen -
 Schriftliches Multiplizieren – Mach mit!
PDF anzeigen
Schriftliches Multiplizieren – Mach mit!
PDF anzeigen -
 Multiplizieren mit Kommazahlen
PDF anzeigen
Multiplizieren mit Kommazahlen
PDF anzeigen -
 Halbschriftliches Multiplizieren – Übungen
PDF anzeigen
Halbschriftliches Multiplizieren – Übungen
PDF anzeigen -
 Schriftliches Multiplizieren – Übungen (1)
PDF anzeigen
Schriftliches Multiplizieren – Übungen (1)
PDF anzeigen -
 Schriftliches Multiplizieren – Übungen (2)
PDF anzeigen
Schriftliches Multiplizieren – Übungen (2)
PDF anzeigen -
 Multiplikation bis 1 Million – Sachaufgaben
PDF anzeigen
Multiplikation bis 1 Million – Sachaufgaben
PDF anzeigen -
 Grundrechenarten bis 1 Million – Sachrechnen zu Grundrechenarten
PDF anzeigen
Grundrechenarten bis 1 Million – Sachrechnen zu Grundrechenarten
PDF anzeigen
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung




















