Hypothesentest – Einführung
"Hypothesentests leicht verständlich erklärt" Erfahre, wie ein Hypothesentest funktioniert und wie er zwischen Bananen verschiedener Qualität unterscheiden kann. Verstehe die Begriffe Nullhypothese, kritischer Wert und Irrtumswahrscheinlichkeit. Interessiert? All das und mehr kannst du im folgenden Text entdecken!


in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.

Grundlagen zum Thema Hypothesentest – Einführung
Die Grundbegriffe des Hypothesentests
Ein Obsthändler verkauft ausschließlich Bananen. Er verkauft Bananen der Güteklasse A. Bei diesen Bananen sind nur $20\%$ kürzer als $14~\pu{cm}$. Er hat aber auch etwas günstigere Bananen der Güteklasse B. Bei diesen Bananen sind $40\%$ kürzer als $14~\pu{cm}$.
Stell dir vor, der Obsthändler erhält eine Lieferung von Kisten mit Bananen erster und Bananen zweiter Wahl – aber die Beschriftung der Kisten ist während der langen Schifffahrt verloren gegangen.
Wie kann er herausfinden, welche die Kiste mit Bananen erster und welche die Kiste mit Bananen zweiter Wahl ist?
Er könnte natürlich alle Bananen einzeln ausmessen. Er kann aber auch Zeit sparen und schlauer vorgehen – er kann einen Hypothesentest durchführen. Was das ist, wollen wir uns im Folgenden anschauen. Dabei wird dir der Hypothesentest einfach erklärt.
Was ist ein Hypothesentest?
Der Hypothesentest ist ein Test aus dem Bereich der Statistik. Mithilfe eines solchen Tests können wir überprüfen, ob eine Hypothese mit einer bestimmten Wahrscheinlichkeit gültig oder ungültig ist. Meistens ist diese Hypothese eine Aussage, die anhand einer Stichprobe über eine statistische Gesamtheit getroffen wird.
Schauen wir uns diese Begriffe anhand unseres Beispiels genauer an.
Als statistische Gesamtheit, manchmal auch Grundgesamtheit genannt, bezeichnen wir die Menge aller Objekte, auf die sich unsere Hypothese bezieht. Über diese Menge möchten wir eine Aussage treffen.
In unserem Beispiel ist die statistische Gesamtheit die Menge aller Bananen einer Kiste. Wir wollen wissen, ob die Menge aller Bananen einer Kiste zur Güteklasse A oder zur Güteklasse B gehört. Bei einem Hypothesentest formulieren wir unsere Frage beziehungsweise Vermutung in Form einer Nullhypothese $H_0$ und einer Alternativhypothese $H_1$.
In unserem Beispiel sähen die Hypothesen folgendermaßen aus:
- Nullhypothese $H_0:$ Die Kiste enthält Bananen der Güteklasse A.
- Alternativhypothese $H_1:$ Die Kiste enthält Bananen der Güteklasse B.
Bei einem Hypothesentest wird in der Regel anhand einer Stichprobe untersucht, ob die Nullhypothese wahr ist. Ist die Wahrscheinlichkeit dafür, dass die Nullhypothese wahr ist, zu gering, so wird davon ausgegangen, dass die Alternativhypothese zutrifft.
In unserem Beispiel wäre die Stichprobe eine Anzahl $n$ an Bananen, die wir zufällig aus der Kiste ziehen. Die Bananen der Stichprobe müssten wir dann auf ihre Größe untersuchen. Die Anzahl an Bananen, die zu kurz sind, ist die Prüfgröße $X$. Anhand dieser Prüfgröße wird entschieden, ob die Nullhypothese angenommen oder abgelehnt wird. Dazu müssen vorher allerdings Entscheidungsregeln aufgestellt werden. Mit diesen legen wir vor dem Ziehen der Stichprobe fest, in welchem Fall wir die Nullhypothese annehmen oder verwerfen.
In unserem Beispiel legen wir eine Anzahl $k$ zu kleiner Bananen fest. Enthält die Stichprobe weniger oder genau $k$ zu kurze Bananen, nehmen wir die Nullhypothese an. Enthält sie mehr, verwerfen wir die Nullhypothese. Der Wert $k$, bis zu dem die Nullhypothese angenommen wird, heißt kritischer Wert des Hypothesentests.
Da in unserem Beispiel bei den Bananen der Güteklasse A nur $20\%$ zu kurz sind, legen wir bei einer Stichprobengröße von $n=30$ den Wert $k$ auf $6$ fest. Also:
$X \leq 6 \Rightarrow H_0 ~ \text{wird angenommen.}$
$X > 6 \Rightarrow H_0 ~ \text{wird verworfen.}$
Wir können die Zahlbereiche, die so entstehen, auf einem Zahlenstrahl abtragen.
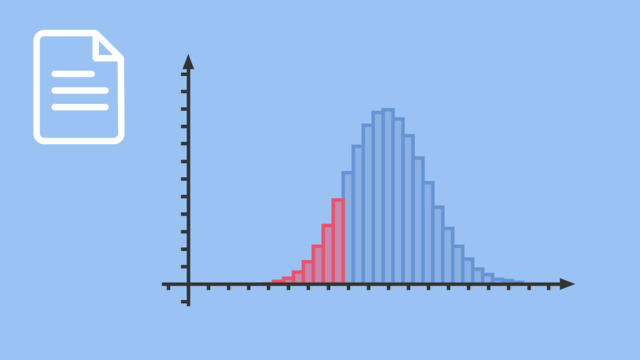
Der Bereich von $0$ bis $6$ heißt Annahmebereich von $H_0$, weil wir für Werte aus diesem Intervall die Nullhypothese annehmen. Der Bereich von $7$ bis $30$ ist hingegen der Verwerfungsbereich von $H_0$ oder der Annahmebereich der Alternativhypothese $H_1$.
Je nachdem, in welchen dieser Bereiche unsere Stichprobe fällt, nehmen wir $H_0$ an oder verwerfen $H_0$. Da wir bei Hypothesentests Zufallsgrößen betrachten, hat unsere Entscheidung allerdings keine $100\%$ige Sicherheit. Es kann zu zwei unterschiedlichen Fehlern kommen: dem Fehler erster Art oder dem Fehler zweiter Art.
Fehler erster Art
Beim Fehler erster Art verwerfen wir die Nullhypothese, obwohl sie eigentlich korrekt ist. Es könnte zum Beispiel passieren, dass wir bei einer Stichprobe von $n=30$ zufällig $7$ zu kurze Bananen aus einer Kiste ziehen, obwohl sie insgesamt weniger als $20\%$ zu kurze Bananen enthält. Nach unserer Entscheidungsregel würden wir $H_0$ verwerfen, obwohl $H_0$ eigentlich korrekt ist. Die Wahrscheinlichkeit für einen Fehler erster Art bezeichnet man mit $\alpha$. Sie hängt vor allem von der Größe der Stichprobe ab.
Fehler zweiter Art
Ein Fehler zweiter Art tritt auf, wenn wir die Nullhypothese annehmen, obwohl sie eigentlich falsch ist. Das wäre in unserem Beispiel der Fall, wenn sich in der Kiste eigentlich Bananen der Güteklasse B befinden, wir aber zufällig nur $4$ zu kurze Bananen in unserer Stichprobe finden. Dann würden wir uns für $H_0$ entscheiden, obwohl eigentlich die Alternativhypothese $H_1$ stimmt. Die Wahrscheinlichkeit für einen Fehler zweiter Art wird mit $\beta$ bezeichnet.
Man nennt $\alpha$ und $\beta$ auch Irrtumswahrscheinlichkeiten. Sie sagen etwas über die Güte des Hypothesentests aus. Je kleiner die Fehler sind, umso höher die Güte, also umso besser der Test. Darum versucht man die Irrtumswahrscheinlichkeiten durch Wahl der Entscheidungsregel oder eine geeignete Stichprobengröße zu minimieren.
Die Irrtumswahrscheinlichkeiten können mithilfe einer Binomialverteilung berechnet werden.
Grundbegriffe des Hypothesentests
Die wichtigsten Begriffe und Sachverhalte zu Hypothesentests fassen wir noch einmal stichpunktartig zusammen:
- Mithilfe eines Hypothesentests können Annahmen über eine statistische Gesamtheit anhand einer Stichprobe getroffen werden.
- Für einen Hypothesentest werden eine Nullhypothese $H_0$ und eine Alternativhypothese $H_1$ aufgestellt.
- Der kritische Wert $k$ gibt an, bis zu welchem Wert der Prüfgröße $X$ die Nullhypothese noch angenommen wird.
- Die Irrtumswahrscheinlichkeit bezeichnet die Wahrscheinlichkeit für Fehler erster bzw. zweiter Art.
Ausblick – das lernst du nach Hypothesentests
Beschäftige dich mit weiteren spannenden Themen aus dem Bereich Stochastik und Statistik wie bedingte Wahrscheinlichkeit, Binomialverteilung und Zufallsgrößen.
In unserem Übungstext zu Hypothesentests kannst du das Gelernte auch direkt anwenden.
Transkript Hypothesentest – Einführung
Sechsundneunzig Prozent der Leute, die sich ein "Peanutbutter-Jelly-Sandwich" machen, schmieren als erstes die Erdnussbutter aufs Brot. Sechsundachtzig Prozent nehmen sich was für den nächsten Tag vor und machen es dann doch nicht. Und zweiundsiebzig Prozent aller Menschen glauben an zufällig ausgewählte Statistiken, wenn man sie ihnen vorlegt. Statistiken, wie diese drei hier, klingen erstmal ziemlich überzeugend. Aber wie können wir denn eigentlich überprüfen, ob sie auch plausibel sind? Dabei kann uns ein sogenannter "Hypothesentest" helfen. Ein Hypothesentest – manchmal auch Signifikanztest genannt – kann dazu dienen, begründete Zweifel an einer Hypothese zu verstärken. Diese Hypothese bezieht sich dann im Mathematikunterricht meistens auf eine Binomialverteilung. Genauer gesagt: Auf die TREFFERWAHRSCHEINLICHKEIT einer Binomialverteilung. Zum Beispiel könnte eine Hypothese lauten, dass zweiundsiebzig Prozent der Menschen an zufällig ausgewählte Statistiken glauben. Die Trefferwahrscheinlichkeit, bei einer zufällig befragten Person eine "statistik-gläubige" zu erwischen, müsste dann bei "p gleich 0,72" liegen. Das ist dann unsere sogenannte "Nullhypothese". Diese Nullhypothese könnten wir jetzt anzweifeln und ihr eine sogenannte Alternativhypothese entgegenstellen, die einen Verdacht widerspiegeln kann. Im einfachsten Fall lautet die Alternativhypothese lediglich, dass die Nullhypothese nicht zutrifft. In unserem Fall also, dass NICHT zweiundsiebzig Prozent der Menschen an Statistiken glauben. Die Grundidee eines Hypothesentests ist dann folgende: Um einen Anhaltspunkt dafür zu bekommen, ob wir die Nullhypothese beibehalten sollten oder sie zugunsten der Alternativhypothese verwerfen können, führen wir eine Stichprobe durch. Dann können wir nämlich betrachten, ob die relative Häufigkeit an Treffern bei der Stichprobe in der Nähe der hypothetischen Trefferwahrscheinlichkeit der Nullhypothese liegt oder nicht. Wie genau das zu verstehen ist, wird klarer, wenn wir uns die Sachlage an einem Beispiel verdeutlichen. Wir betrachten den Fall, dass wir einhundert zufällig ausgewählte Menschen befragen. Unter der Voraussetzung, dass unsere Nullhypothese stimmt, p also gleich 0,72 ist, sieht die Binomialverteilung als Histogramm dargestellt, dann SO aus. Der Erwartungswert, der in diesem Fall der Trefferanzahl mit der höchsten Wahrscheinlichkeit entspricht, liegt dann bei zweiundsiebzig. Die Trefferzahlen links und rechts davon werden Säule für Säule immer unwahrscheinlicher. Je weiter sie vom Erwartungswert entfernt sind, desto unwahrscheinlicher sind diese Ergebnisse unter Voraussetzung der Nullhypothese. Bei dieser Verteilung sind die Werte unter sechzig und über achtzig schon sehr unwahrscheinlich. Und genau diese Tatsache macht sich der Hypothesentest zu Nutze. Wenn wir die Stichprobe tatsächlich durchführen und dabei zum Beispiel nur fünfzig Treffer landen, ist das ein sehr unwahrscheinliches – wenn auch nicht unmögliches – Resultat, vorausgesetzt die Trefferwahrscheinlichkeit liegt tatsächlich bei zweiundsiebzig Prozent. Ein plausibler Erklärungsansatz wäre dann, dass die Trefferwahrscheinlichkeit in Wahrheit NICHT gleich 0,72 ist. Der Hypothesentest legt dann nahe, die Nullhypothese zu verwerfen und die Alternativhypothese anzunehmen! Um sich bei der Entscheidung, die Nullhypothese zu verwerfen oder beizubehalten, nicht von dem Ergebnis der Stichprobe beeinflussen zu lassen, legt man grundsätzlich VOR der Durchführung der Stichprobe fest, welche Trefferzahlen zum Beibehalten und welche Trefferzahlen zum Verwerfen der Nullhypothese führen sollen. Das heißt ganz konkret: Wir unterteilen die Binomialverteilung in einen ANNAHME- und einen ABLEHNUNGsbereich. An DIESEN Bereichen wird dann nach der Durchführung der Stichprobe nicht mehr gerüttelt, wodurch ein konkretes Ergebnis dann eindeutig zum Beibehalten oder Ablehnen der Nullhypothese führt. Ganz wichtig ist es, hierbei zu betonen, dass wir durch einen Hypothesentest eine Hypothese aber nicht zu einhundert Prozent beweisen oder widerlegen können. Wir können nicht sagen, ob die Trefferwahrscheinlichkeit in Wirklichkeit 0,6, 0,7 oder 0,8 beträgt oder wie wahrscheinlich es ist, dass sie genau bei 0,72 liegt. Wir können nur sagen, wie hoch die Wahrscheinlichkeit dafür ist, dass die entsprechende Stichprobe bei der vermuteten Trefferwahrscheinlichkeit von 0,72 eintritt. Erhalten wir nur fünfzig Treffer, obwohl eine Trefferanzahl in der Nähe von zweiundsiebzig zu erwarten gewesen wäre, lehnen wir die Nullhypothese ab, weil fünfzig Treffer bei einer tatsächlichen Trefferwahrscheinlichkeit von 0,72 sehr unwahrscheinlich wären. Das Ergebnis ist aber auch, wenn die Nullhypothese zutrifft, nicht unmöglich und es führt auch NICHT dazu, dass wir davon ausgehen könnten, die Trefferwahrscheinlichkeit läge in Wirklichkeit bei 0,5. Hypothesentests sind daher mit Vorsicht zu genießen und bieten lediglich einen Anhaltspunkt dazu, ob eine Hypothese zu einer Stichprobe passend erscheint oder nicht. Das ist dann aber auch erstmal alles, was du für ein grundlegendes Verständnis von Hypothesentests wissen musst! Wir fassen nochmal zusammen: Es geht bei Hypothesentests also darum, eine Nullhypothese, die sich auf die zugrundeliegende Trefferwahrscheinlichkeit bezieht und die gegebenenfalls aus bestimmten Gründen angezweifelt wird, beizubehalten oder zu verwerfen und eine Alternativhypothese anzunehmen. Ab welchen Ergebnissen es zu einer Verwerfung der Nullhypothese kommt, wird vor der Durchführung einer Stichprobe anhand bestimmter Kriterien festgelegt, die zu einem klar definierten Annahme- und Ablehnungsbereich führen. Dann haben wir NACH der Durchführung eine klare Aussage darüber, ob das Ergebnis unter diesen Kriterien zu der Nullhypothese passt oder nicht. Wie die Kriterien zur Festlegung von Annahme- und Ablehnungsbereich aussehen können – hierzu lautet das Stichwort "Signifikanzniveau" – warum und wie wir zwischen einseitigen und beidseitigen Hypothesentests unterscheiden und was es mit den sogenannten Fehlern erster und zweiter Art auf sich hat, erfährst du in den weiteren Videos dieser Reihe. Aber keine Sorge! Wenn du die Grundidee von Hypothesentests einmal verstanden hast, sind dann auch diese Fachbegriffe keine große Hürde mehr.
Hypothesentest – Einführung Übung
-
Gib die Bezeichnungen der Größen beim Hypothesentest an.
TippsDie Nullhypothese besagt, dass die Vermutung über den Wert der Trefferwahrscheinlichkeit gilt.
Die Alternativhypothese besagt, dass die Nullhypothese nicht gilt.
LösungEinem Hypothesentest liegt in der Schulmathematik meistens eine Binomialverteilung zugrunde. Diese beruht auf einem Bernoulli-Experiment, also einem Zufallsexperiment mit nur zwei möglichen Ergebnissen. Die Wahrscheinlichkeit eines der beiden Ergebnisse ist die Trefferwahrscheinlichkeit $p$.
$\Rightarrow$ Die Trefferwahrscheinlichkeit beträgt hier $\boldsymbol{p=0,\!72}$.Mit einem Hypothesentest wird die Gültigkeit einer Hypothese über diese Trefferwahrscheinlichkeit getestet, also einer Aussage über den Wert von $p$. Das ist die Nullhypothese $H_0$.
$\Rightarrow$ Die Nullhypothese $H_0$ ist die Aussage $\boldsymbol{H_0}$: $\boldsymbol{p=0,\!72}$.Die Alternativhypothese $H_1$ ist die Negation der Nullhypothese $H_0$.
$\Rightarrow$ Die Alternativhypothese lautet also $\boldsymbol{H_1}$: $\boldsymbol{p\neq 0,\!72}$.Bei der Durchführung des Hypothesentests werden Daten erhoben. Der Umfang des Datensatzes heißt Stichprobenumfang $n$.
$\Rightarrow $ Der Stichprobenumfang beträgt $\boldsymbol{n=100}$. -
Beschreibe das Vorgehen bei Hypothesentests.
TippsDie Binomialverteilung beschreibt die Wahrscheinlichkeiten von Trefferanzahlen bei mehrmaliger Durchführung von Bernoulli-Experimenten.
Die Nullhypothese beim Werfen einer fairen Münze ist die Annahme $p=0,\!5$.
Zur Auswertung des Hypothesentests wird die Trefferzahl in einer Stichprobe erhoben.
LösungEin Hypothesentest kann verwendet werden, um Zweifel an einer gängigen Annahme zu bestätigen oder auszuräumen. In der Schulmathematik liegt einem Hypothesentest meistens eine Binomialverteilung zugrunde. Getestet wird eine Annahme über den Wert der Trefferwahrscheinlichkeit $\boldsymbol{p}$ des zugehörigen Bernoulli-Experiments.
Zur Konstruktion eines Hypothesentests wird zuerst eine sogenannte Nullhypothese $\boldsymbol{H_0}$ benötigt. Dies ist eine Annahme über den Wert der Trefferwahrscheinlichkeit $p$, zum Beispiel die Annahme $H_0$: $p=0,\!72$. Anhand des Hypothesentests wird diese Annahme bestätigt oder verworfen.
Der Verdacht, dass die Annahme falsch ist, wird als Alternativhypothese $\boldsymbol{H_1}$ formuliert. In unserem Beispiel ist die Alternativhypothese beispielsweise die Aussage $H_1$: $p \neq 0,\!72$.
Bei der Durchführung eines Hypothesentests wird eine Stichprobe untersucht. Die Feststellung, ob die Stichprobe zum Annahmebereich oder zum Ablehnungsbereich des Tests gehört, ergibt das Testergebnis.
-
Interpretiere den Hypothesentest auf Basis der Stichprobe.
TippsEs sind drei Aussagen korrekt.
Der Ablehnungsbereich besteht aus allen Werten $k$, bei denen die Nullhypothese abgelehnt wird.
Bei dieser Stichprobe führt ein Wert von $k=85$ zum Ablehnen der Nullhypothese.
Der Wert $k$ mit der höchsten Wahrscheinlichkeit ist nicht der einzige Wert, für den die Nullhypothese beibehalten wird.
LösungFolgende Aussagen sind richtig:
- Bei einem Wert von $k=67$ wird die Nullhypothese verworfen.
- Bei einem Wert von $k=51$ wird die Nullhypothese beibehalten.
- Die Trefferzahl $k=56$ gehört als Erwartungswert zum Annahmebereich.
Folgende Aussagen sind falsch:
- Ein Wert von $k=56$ bestätigt die Alternativhypothese.
- Nur dann, wenn $k=56$ ist, wird die Nullhypothese bestätigt.
-
Stelle das Vorgehen für einen Hypothesentest bei dieser neuen Studie dar.
TippsLege bei einem Hypothesentest immer zuerst die Nullhypothese fest.
Zur Bestimmung des Annahmebereichs $A$ und des Ablehnungsbereichs $\overline A$ benötigst du die Binomialverteilung.
Verwerfen oder Behalten der Nullhypothese sind die beiden letzten Schritte des Hypothesentests.
LösungZur Durchführung eines Hypothesentests auf Grundlage einer Binomialverteilung benötigst du zuerst eine Nullhypothese $H_0$ über den Wert $p$ der Trefferwahrscheinlichkeit. Die Alternativhypothese $H_1$ ist dann die Negation dieser Annahme. In unserem Beispiel lautet die Nullhypothese $H_0$: $p=0,\!57$ und die Alternativhypothese ${H_1}$: ${p\neq 0,\!57}$.
Hast du die Hypothesen formuliert, berechnest du die Binomialverteilung mit den Parametern $n$ (Stichprobenumfang) und $p$ (Trefferwahrscheinlichkeit). In dieser Aufgabe ist $p=0,\!57$ und $n=100$.
Mit dem Histogramm der Binomialverteilung legst du den Annahmebereich $A$ und den Ablehnungsbereich $\overline A$ der Nullhypothese fest. Erst danach nimmst du die Stichprobe und bestimmst die Trefferzahl $x$.
Du prüfst nun, ob der Treffer der Stichprobe zum Annahmebereich $A$ oder zum Ablehnungsbereich $\overline A$ der Nullhypothese gehört, das heißt, ob $x \in A$ oder $x\in \overline A$ gilt.
Ist $x \in \overline A$, liegt also die Stichprobe im Ablehnungsbereich der Nullhypothese, wird die Nullhypothese $H_0$ zugunsten der Alternativhypothese $H_1$ verworfen. Andernfalls behältst du die Nullhypothese bei.
Du erhältst somit folgende korrekte Reihenfolge:
1) Formuliere Nullhypothese $H_0$: $p=0,\!57$ und Alternativhypothese $H_1$: $p\neq 0,\!57$.
2) Bestimme die Binomialverteilung mit $n=100$ und $p=0,\!57$.
3) Lege den Annahmebereich $A$ und den Ablehnungsbereich $\overline A$ fest.
4) Ziehe eine Stichprobe und ermittle die Trefferzahl $x$.
5) Überprüfe, ob $x \in A$ oder $x \in \overline A$ gilt, und entscheide entsprechend, die Nullhypothese beizubehalten oder zu verwerfen.
-
Benenne die Bereiche des Hypothesentests im Histogramm.
TippsDer Erwartungswert der Verteilung gehört zum Annahmebereich.
Der Ablehnungsbereich besteht aus besonders unwahrscheinlichen Ereignissen.
Der Annahmebereich liegt in der Mitte des Histogramms.
LösungZur Durchführung eines Hypothesentests legt man den Annahmebereich und den Ablehnungsbereich der Nullhypothese fest. Der Ablehnungsbereich kann auch aus mehreren einzelnen Bereichen bestehen.
Im Histogramm ist der Annahmebereich grün dargestellt. Liegt das Testergebnis in diesem Bereich, gilt die Nullhypothese als bestätigt.
Der Ablehnungsbereich ist rot dargestellt und besteht hier aus zwei einzelnen Bereichen. Liegt das Testergebnis im Ablehnungsbereich, wird die Nullhypothese zugunsten der Alternativhypothese verworfen.Im Bild siehst du die korrekt bezeichneten Bereiche.
-
Analysiere die Aussagen zu Hypothesentests.
TippsZwei Aussagen sind korrekt.
Bei einem Hypothesentest bezieht sich die Entscheidung über Bestätigen oder Verwerfen immer auf die Nullhypothese und nicht auf die Alternativhypothese.
Ein Hypothesentest ist in der Regel nicht symmetrisch.
LösungFolgende Aussagen sind richtig:
- Ein Hypothesentest kann Zweifel an der Nullhypothese bestätigen, liefert aber keine hundertprozentige Sicherheit.
- Nur dann, wenn der Hypothesentest Zweifel an der Nullhypothese bestätigt, wird die Nullhypothese verworfen
Folgende Aussagen sind falsch:
- Ein Hypothesentest erlaubt die Entscheidung zwischen drei Alternativen.
Für eine weitere Alternativhypothese wird ein zusätzlicher Test benötigt.- Bei einem Hypothesentest wird die Alternativhypothese bestätigt oder verworfen.
- Bei der Konstruktion eines Hypothesentests kann man Nullhypothese und Alternativhypothese beliebig vertauschen.
9.711
sofaheld-Level
6.600
vorgefertigte
Vokabeln
8.276
Lernvideos
38.589
Übungen
33.616
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Klassenstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung





 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?















SUPER , DANKE !!!!!