Der Satz des Pythagoras
Erfahre alles über den berühmten Satz des Pythagoras, der in rechtwinkligen Dreiecken gilt. Lerne die Bedeutung von Hypotenuse und Katheten sowie die Formel $a^2 + b^2 = c^2$. Berechne fehlende Seitenlängen und entdecke pythagoreische Tripel. Interessiert? Dies und mehr im folgenden Text!
in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.

Grundlagen zum Thema Der Satz des Pythagoras
Der Satz des Pythagoras – Einführung
Der Satz des Pythagoras ist sicher einer der bekanntesten Sätze der Mathematik. Dieser Satz gilt ausschließlich in rechtwinkligen Dreiecken.
Bezeichnungen in rechtwinkligen Dreiecken
- Die längste Seite in einem rechtwinkligen Dreieck wird Hypotenuse genannt. Sie liegt dem rechten Winkel gegenüber.
- Die beiden anderen Seiten sind die Katheten. Sie liegen an dem rechten Winkel an.
- Es gibt in rechtwinkligen Dreiecken also eine Hypotenuse und zwei Katheten.
Der Satz des Pythagoras formuliert einen Zusammenhang zwischen den Flächeninhalten der Quadrate über den Seiten eines rechtwinkligen Dreiecks und somit auch einen Zusammenhang über die Seiten des rechtwinkligen Dreiecks.
Der Satz des Pythagoras – Definition

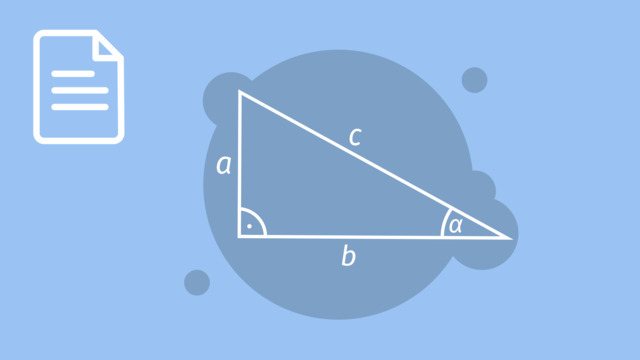
In dem abgebildeten Dreieck sind die Seiten $a$ und $b$ die Katheten und $c$ die Hypotenuse.
Die Flächeninhalte der Quadrate über den Katheten sind $a^2$ sowie $b^2$. Der Flächeninhalt des Quadrats über der Hypotenuse ist $c^2$. Werden die Kathetenquadrate addiert zu $a^2+b^2$, kommt der gleiche Flächeninhalt heraus wie der des Hypotenusenquadrates $c^2$.
Als Formel ausgedrückt: $a^2+b^2=c^2$
In Worten: In einem rechtwinkligen Dreieck gilt, dass die beiden Kathetenquadrate gemeinsam den gleichen Flächeninhalt haben wie das Hypotenusenquadrat.
Der Satz des Pythagoras – Anwendungen
Wenn in einem rechtwinkligen Dreieck zwei Seitenlängen gegeben sind, kann die fehlende dritte Seitenlänge mithilfe des Satzes des Pythagoras berechnet werden.
Beispiel – beide Kathetenlängen sind gegeben
Die beiden Katheten haben die Längen $a=20~\text{cm}$ und $b=21~\text{cm}$. Gesucht ist die Länge der Hypotenuse $c$.
- Die gegebenen Größen werden in den Satz des Pythagoras eingesetzt: $\left(20~\text{cm}\right)^2+\left(21~\text{cm}\right)^2=c^2$
- Berechnung der Quadrate: $400~\text{cm}^2+441~\text{cm}^2=c^2$
- Berechnung der Summe: $841~\text{cm}^2=c^2$
- Um die Länge der Hypotenuse zu berechnen, muss die Wurzel aus $841~\text{cm}^2$ gezogen werden: $\sqrt{841~\text{cm}^2}=29\text{cm}$
Die Länge der Hypotenuse ist $c=29~\text{cm}$. Beim Ziehen der Quadratwurzel muss auch die Gegenzahl $-29$ betrachtet werden. Diese Lösung kann allerdings vernachlässigt werden, da es sich hier um Längen handelt.
Beispiel – eine Kathetenlänge sowie die Hypotenusenlänge sind gegeben
Die eine Kathete sei $a=35~\text{cm}$ und die Hypotenuse $c=37~\text{cm}$. Gesucht ist die Länge der anderen Kathete $b$.
- Die gegebenen Größen werden in den Satz des Pythagoras eingesetzt: $\left(35~\text{cm}\right)^2+b^2=\left(37~\text{cm}\right)^2$.
- Berechnung der Quadrate: $1225~\text{cm}^2+b^2=1369~\text{cm}^2$
- Subtraktion von $1225~\text{cm}^2$ und Berechnung der Differenz: $b^2=1369~\text{cm}^2-1225~\text{cm}^2=144~\text{cm}^2$
- Zuletzt muss wieder die Wurzel gezogen werden: $b=\sqrt{144~\text{cm}^2}=12~\text{cm}$
Der Satz des Pythagoras – Ausblick
Wenn du das Gelernte direkt anwenden und einüben möchtest, schau am besten mal bei unserem Übungstext zum Satz des Pythagoras vorbei. Ansonsten erfährst du hier weitere wichtige weiterführende Informationen:
Die Umkehrung des Satzes des Pythagoras
Der Satz des Pythagoras besagt auch: Wenn die Summe der Quadrate zweier Seitenlängen in einem Dreieck gleich dem Quadrat der dritten Seitenlänge ist, liegt ein rechtwinkliges Dreieck vor.
Wenn ein Seil der Länge $120~\text{cm}$ durch Markierungen in Teilstücke der Längen $30~\text{cm}$, $40~\text{cm}$ und $50~\text{cm}$ unterteilt wird, können diese Teilstücke zu einem rechtwinkligen Dreieck zusammengelegt werden.
Pythagoreische Tripel
In den beiden obigen Beispielen bilden die Seiten der Längen $20~\text{cm}$, $21~\text{cm}$ und $29~\text{cm}$ sowie $12~\text{cm}$, $35~\text{cm}$ und $37~\text{cm}$ die Seiten eines rechtwinkligen Dreiecks. Natürlich müssen die Seiten eines rechtwinkligen Dreiecks nicht immer natürliche Zahlen sein.
Eine Anordnung von drei natürlichen Zahlen, die den Satz des Pythagoras erfüllen, wird als pythagoreisches Tripel bezeichnet:
- $3^2+4^2=5^2$
- $20^2+21^2=29^2$
- $12^2+35^2=37^2$
Es gibt unendlich viele solcher pythagoreischer Tripel.
Der Satz des Pythagoras – Zusammenfassung
Nach dem Schauen dieses Videos wirst du in der Lage sein, mithilfe des Satzes des Pythagoras die Hypotenuse eines rechtwinkligen Dreiecks auszurechnen.
Zunächst lernst du, wie die Seiten im rechtwinkligen Dreieck bezeichnet werden. Anschließend wird der Satz des Pythagoras aufgestellt. Abschließend wird ein Beispiel durchgerechnet.
Bevor du dieses Video schaust, solltest du bereits wissen, welche Eigenschaften rechtwinklige Dreiecke haben, wie man die Fläche von Quadraten ausrechnet und wie man quadriert und Wurzeln zieht.
Nach diesem Video wirst du darauf vorbereitet sein, weitere Berechnungen in geometrischen Figuren kennenzulernen.
Transkript Der Satz des Pythagoras
Ronny wartet im Auto auf seine Komplizin Gisela. Die raubt gerade eine Bank aus. ALARM! Jemand hat die Polizei verständigt! Kein Problem, die beiden haben einen Plan B. Gisela seilt sich einfach aus dem Fenster ab. Dazu muss Ronny nur wissen, wie lang das Seil sein muss. Um das herauszufinden, wendet Ronny den Satz des Pythagoras an. Das Seil darf nicht zu kurz sein, sonst reicht es nicht bis an das Fenster. Es darf aber auch nicht zu lang sein, denn sonst hängt es durch. Es muss also genau so lang sein, wie die Strecke vom Auto zum Fenster. Dabei handelt es sich um die längste Seite eines rechtwinkligen Dreiecks. Die nennt man auch Hypotenuse. Die beiden anderen Seiten des rechtwinkligen Dreiecks, die am rechten Winkel anliegen, heißen Katheten. Die Längen der Katheten stehen in einem besonderen Zusammenhang mit der Länge der Hypotenuse. Der wird im Satz des Pythagoras beschrieben: Dieser besagt, dass die beiden Kathetenquadrate zusammen dieselbe Fläche haben, wie das Quadrat der Hypotenuse. Die Flächen der beiden Kathetenquadrate sind 'a Quadrat' und 'b Quadrat'. Zusammen sind sie genauso groß wie 'c Quadrat', also die Fläche des Hypotenusenquadrats. Weil die Flächen der Quadrate durch ihre Seitenlängen vollständig bestimmt sind, beschreibt der Satz des Pythagoras auch die Beziehung der Dreieckslängen. Er gilt aber nur in rechtwinkligen Dreiecken. Na dann schauen wir doch mal, ob wir die Länge des Seils ausrechnen können. Ronny hat das Fluchtauto 63 Meter vom Bankgebäude entfernt geparkt. Das Fenster, aus dem sich Gisela abseilen will, hat eine Höhe von 16 Metern. Wir setzen diese beiden Werte ein, quadrieren und addieren die Summanden. Damit wissen wir, wie groß das Quadrat der Hypotenuse ist. Um die Länge der Hypotenuse auszurechnen, müssen wir nun noch die Wurzel ziehen. Weil das Quadrieren einer negativen Zahl zum selben Ergebnis führt, wie das Quadrieren der positiven Gegenzahl, ergeben sich zwei mögliche Lösungen. Weil wir hier aber nach einer Länge suchen, ist die negative Lösung nicht sinnvoll. Wir geben daher nur die positive Lösung an. Die Wurzel aus 4225 ist 65. Das Seil muss also genau 65 Meter lang sein. Und geschafft! Gisela flieht mit der Beute und wir fassen zusammen: In einem rechtwinkligen Dreieck heißt die längste Seite Hypotenuse. Sie liegt dem rechten Winkel gegenüber. Die beiden anderen Seiten, die am rechten Winkel anliegen, heißen Katheten. Der Satz des Pythagoras besagt, dass die Fläche der Kathetenquadrate zusammen genauso groß ist, wie die Fläche des Hypotenusenquadrats. a Quadrat' plus 'b Quadrat' ist also 'c Quadrat'. Die Fläche eines Quadrats wird nur von der Seitenlänge des Quadrats bestimmt. Deshalb beschreibt der Satz des Pythagoras auch eine Beziehung zwischen den Seitenlängen eines rechtwinkligen Dreiecks. Haben wir also die Längen der Katheten eines rechtwinkligen Dreiecks gegeben, können wir die Länge der Hypotenuse einfach ausrechnen. Dabei musst du aber immer beachten: Der Satz des Pythagoras gilt nur in rechtwinkligen Dreiecken! Gisela hat das Fluchtauto erreicht. Aber wieso können sie nicht losfahren? Ronny! Warum parkst du auch ausgerechnet im Halteverbot? Das war wohl eine Idee zu viel krimineller Energie.
Der Satz des Pythagoras Übung
-
Ergänze die Seiten und Flächeninhalte.
TippsDie kürzeste Seite eines rechtwinkligen Dreiecks heißt Kathete.
Die Fläche eines Quadrates mit der Kantenlänge $x$ ist $x^2$.
Der Flächeninhalt des Quadrates über der Hypotenuse entspricht der Summe der Flächeninhalte der Quadrate über den Katheten.
LösungDer Satz des Pythagoras drückt den Flächeninhalt des Quadrates über der Hypotenuse eines rechtwinkligen Dreiecks durch den Flächeninhalt der Quadrate über den Katheten aus. Üblicherweise werden die Katheten mit $a$ und $b$ bezeichnet und die Hypotenuse mit $c$. Der Flächeninhalt eines Quadrates mit Kantenlänge $x$ ist $x^2$. Somit haben die Quadrate über den Katheten die Flächeninhalte $a^2$ bzw. $b^2$, das Quadrat über der Hypotenuse den Flächeninhalt $c^2$. Der Satz des Pythagoras ist die folgende Formel für die Flächeninhalte:
$a^2+b^2=c^2$
-
Bestimme die Seitenlängen und Flächeninhalte.
Tipps$c$ ist die längste der drei Seiten und somit die Hypotenuse des abgebildeten rechtwinkligen Dreiecks.
Berechne das Quadrat der Seitenlängen $a$ und $b$.
Hier ist eine Beispielrechnung: In dem rechtwinkligen Dreieck mit den Katheten $a = 5~\text{cm}$ und $b = 12~\text{cm}$ gilt:
$c = \sqrt{(5~\text{cm})^2+(12~\text{cm})^2} = \sqrt{25~\text{cm}^2+144~\text{cm}^2} = \sqrt{169~\text{cm}^2} = 13~\text{cm}$
LösungMit dem Satz des Pythagoras kannst du die Länge der Hypotenuse aus den Längen beider Katheten ausrechnen. Heißen die Katheten $a$ und $b$ und die Hypotenuse $c$, so gilt:
- $a^2+b^2=c^2$
Setzt du $a=16~\text{m}$ und $b=63~\text{m}$ in den Term $a^2+b^2$ ein, so ergibt sich:
- $c^2 = (16~\text{m})^2 + (63~\text{m})^2= 256~\text{m}^2+3.969~\text{m}^2=4.225~\text{m}^2$
- $c=\sqrt{4. 225~\text{m}^2} = 65~\text{m}$
-
Ermittle die Längen der Hypotenusen.
TippsSetze die Werte von $a$ und $b$ ein und berechne die Quadrate $a^2$ und $b^2$.
Die Hypotenuse ist die Wurzel aus der Summe der Quadrate der Katheten, d.h. $c = \sqrt{a^2+b^2}$.
Hier ist eine Beispielrechnung: Mit $a= 12$ und $b=5$ ist $a^2 = 144$ und $b=25$. Daher ist $c = \sqrt{a^2+b^2} = \sqrt{144+25} = \sqrt{169} = 13$.
LösungDu kannst die Werte für die Katheten $a$ und $b$ in die Quadrate einsetzen und so die Flächeninhalte der Kathetenquadrate bestimmen. Dann addierst du diese und erhältst den Flächeninhalt des Hypotenusenquadrats. Ziehst du daraus die Wurzel, so erhältst du die Länge der Hypotenuse:
- Mit den Katheten $a=7$ und $b=24$ erhältst du die Kathetenquadrate $a^2 =7^2 = 49$ und $b^2= 24^2=576$. Das Hypotenusenquadrat ist dann $c^2 = a^2+b^2 = 49+576 = 625$. Die Hypotenuse ist schließlich $c=\sqrt{a^2+b^2}= \sqrt{625} =25$.
- Die Quadrate der Katheten $a=8$ und $b=15$ sind $a^2 = 8^2=64$ und $b^2=15^2=225$. Das zugehörige Quadrat der Hypotenuse ist dann $c^2= 64+225 = 289$. Die Hypotenuse hat daher die Länge $c=\sqrt{289} = 17$.
- Zu den Katheten $a=21$ und $b=20$ gehören die Quadrate $a^2=21^2=441$ und $b^2=20^2=400$. Die Hypotenuse hat dann die Länge $c = \sqrt{400+441} =29$.
-
Setze die Katheten mit den Hypotenusen in Beziehung.
TippsDie Hypotenuse ist stets länger als beide Katheten.
Zu einer ganzzahligen und einer nicht ganzzahligen Kathete passt keine ganzzahlige Hypotenuse.
LösungDer Satz des Pythagoras lautet für ein rechtwinkliges Dreieck mit den Katheten $a$ und $b$ und der Hypotenuse $c$ wie folgt:
$a^2+b^2 = c^2$
Du kannst die Formel benutzen, um aus je zwei gegebenen Seiten die dritte auszurechnen.
In dieser Aufgabe ist aber jeweils nur eine Seite vorgegeben und die beiden anderen dazu passenden gesucht. Auch dafür kannst du den Satz des Pythagoras verwenden. Um nicht alle Möglichkeiten einzeln durchprobieren zu müssen, kannst du zusätzlich Folgendes verwenden: Die Hypotenuse $c$ ist stets die längste Seite des rechtwinkligen Dreiecks. Die Kathete $b=12$ kann daher zu keiner anderen Hypotenuse als $c=13$ gehören. Außerdem ist die Hypotenuse kürzer als die Summe der Katheten, sonst würde sich das Dreieck nicht schließen. Zu der Hypotenuse $c=13$ und der Kathete $b=12$ passt also nicht die Kathete $a=0,8$, denn für diese ist $a+b = 12,8 < 13$. Ferner ist das Quadrat einer Kommazahl wieder eine Kommazahl. Sind also zwei der drei Längen eines Dreiecks ganzzahlig, so kann die dritte Länge keine Kommazahl sein: Zu der Hypotenuse $c=13$ und der Kathete $b=12$ passt also nicht die Kathete $a=2,4$, denn sonst wäre $a^2 + b^2$ eine Kommazahl, aber $c^2$ ist keine Kommazahl.
So findest du folgende Zuordnungen:
$c=5$:
- $a=3$
- $b=4$
- Für diese Werte ist $a^2+b^2 = 9+16 = 25 = c^2$.
- $a=5$
- $b=12$
- Hier ist $a^2 + b^2 = 25+144 = 169 = c^2$.
- $a=2,4$
- $b=3,2$
- Diese Werte ergeben $a^2 + b^2 = 5,76+10,24 = 16 = c^2$.
- $a=0,8$
- $b=0,6$
- Hier ergibt sich $a^2 + b^2 = 0,64 + 036 = 1 = c^2$.
-
Zeige die geometrischen Größen.
TippsDer größte Winkel liegt der längsten Seite gegenüber.
In einem rechtwinkligen Dreieck ist der rechte Winkel der größte der drei Winkel.
Die am rechten Winkel anliegenden Seiten heißen Katheten.
LösungIn einem rechtwinkligen Dreieck gibt es jeweils einen speziellen Winkel und eine spezielle Seite: Der rechte Winkel ist stets der größte Winkel im rechtwinkligen Dreieck und hat die Winkelgröße $90^\circ$. Die beiden anderen Winkel sind spitze Winkel, d. h. sie haben eine Winkelgröße $< 90^\circ$.
Die Seite gegenüber dem rechten Winkel heißt Hypotenuse, die beiden anderen Seiten sind die Katheten.
-
Prüfe die Formeln.
TippsDer Satz des Pythagoras gilt nur in rechtwinkligen Dreiecken.
LösungDer Satz des Pythagoras gilt in rechtwinkligen Dreiecken. Für jedes nicht-rechtwinklige Dreieck ist die Formel aus dem Satz des Pythagoras falsch.
Folgende Bilder sind richtig beschriftet:
2. Das Dreieck ist rechtwinklig mit den Katheten $x$ und $y$ und der Hypotenuse $z$.
4. Das Dreieck ist rechtwinklig mit den Katheten $a$ und $b$ und der Hypotenuse $c$. Du kannst die Formel $a^2+b^2=c^2$ nach $b^2$ auflösen und die Wurzel ziehen.
6. Das Bild zeigt eine geometrische Beweisidee für den Satz des Pythagoras: Die vier Dreiecke sind kongruent, du kannst jedes der vier benutzen, um die Formel zu überprüfen. Das Quadrat in der Mitte hat die Fläche $c^2$. Das äußere Quadrat hat die Fläche $(a+b)^2$. Jedes der Dreiecke hat die Fläche $\frac{1}{2} ab$, zusammen haben die vier Dreiecke also die Fläche $4 \cdot \frac{1}{2} ab = 2ab$. Die Fläche des großen Quadrates abzüglich der Dreiecke ist daher $(a+b)^2 - 2ab = (a^2+2ab+b^2) -2ab = a^2+b^2$. Andererseits ist diese Fläche genau das innere Quadrat, also $c^2$.
Folgende Bilder sind falsch beschriftet:
1. Das Dreieck ist nicht rechtwinklig, daher gilt der Satz des Pythagoras in diesem Dreieck nicht.
3. Das Dreieck ist rechtwinklig und gleichschenklig. Daher ist $a=b$ und daher $c = \sqrt{a^2+a^2} = \sqrt{2a^2} = \sqrt{2}a \neq 2a$.
5. Die Diagonale $d$ des Rechtecks ist die Hypotenuse des rechtwinkligen Dreiecks mit den Katheten $a$ und $b$. Daher ist nach dem Satz des Pythagoras $d^2=a^2+b^2\neq (a+b)^2$.
9.592
sofaheld-Level
6.600
vorgefertigte
Vokabeln
8.299
Lernvideos
38.698
Übungen
33.670
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Klassenstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung




 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?
















Fantastisch erklärt sehr verständlich danke!
Danke!!!
jetzt ist mir alles klar ,danke super erklärung
Gut
tolles video, hab alles gut verstanden