Abstand zweier Punkte – Herleitung (Satz des Pythagoras)


in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
Grundlagen zum Thema Abstand zweier Punkte – Herleitung (Satz des Pythagoras)
Nach diesem Video wirst du in der Lage sein, den Abstand zweier Punkte zu berechnen. Zunächst leiten wir ausgehend von dem Satz des Pythagoras die Formel für die Berechnung des Abstandes zweier Punkte her. Anschließend lernst du mittels unterschiedlicher Beispiele, wie du diese Formel anwendest. Abschließend erhältst du einen Überblick über das gesamte Vorgehen. Lerne mit den Drachen, wie du die kürzeste Distanz zwischen zwei Orten ermitteln kannst.
Transkript Abstand zweier Punkte – Herleitung (Satz des Pythagoras)
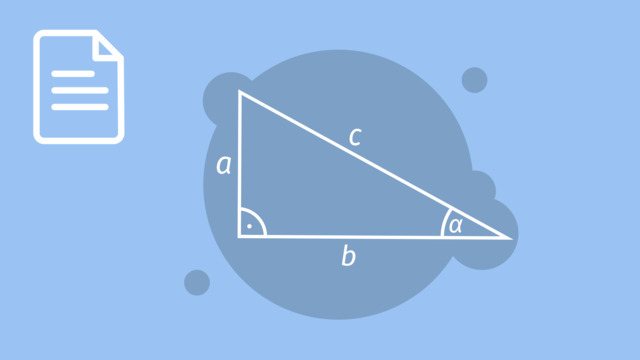
Zu Ehren der Drachen, die ihnen großes Glück beschert haben, haben die Bewohner von Nanjie auf einem Berg einen prachtvollen Tempel errichtet. Nun veranstalten sie eine pompöse Parade von Nanjie zum Fuß des Tempelberges. Der Weg dorthin führt sie um den großen See herum, die Drachen können einfach darüber hinwegfliegen. Um die Entfernungen zu berechnen, werden wir die Herleitung der Formel für den Abstand zweier Punkte aus dem Satz des Pythagoras nutzen. Betrachten wir die Strecke im Koordinatensystem, jede Einheit entspricht 1 Kilometer. Das Dorf liegt in Punkt B. Der Fuß des Tempelberges liegt in Punkt A. Die Dorfbewohner nehmen den Weg um den See herum, sie biegen im Punkt C ab. Wie weit müssen die Dorfbewohner gehen? Wir zählen von 2 bis 10 und sehen, dass die Strecke 8 Kilometer lang ist. Dann zählen wir von 1 bis 7 und sehen, dass diese Strecke 6 Kilometer lang ist. Die Dorfbewohner müssen also 14 Kilometer gehen, um zum Tempelberg zu kommen. Die Drachen haben eine kürzere Reise vom Punkt B zum Fuß des Berges in Punkt A. Wir können aber nicht einfach die Kästchen dieser Diagonalen im Koordinatensystem zählen. Um diese Strecke zu ermitteln, müssen wir unser geometrisches Wissen heranziehen. Erkennst du in dieser Abbildung eine bekannte Form? Richtig, die Form ist ein rechtwinkliges Dreieck. Und welche Formel beschreibt das Verhältnis der Seiten eines rechtwinkligen Dreiecks? Der Satz des Pythagoras besagt: In einem rechtwinkligen Dreieck beträgt das Quadrat der Hypotenuse, also der längsten Seite im rechtwinkligen Dreieck, der Summe der Kathetenquadrate. Das können wir als Formel schreiben. Wir haben die beiden Katheten a und b und die Hypotenuse c. Dann gilt: a Quadrat plus b Quadrat gleich c Quadrat. Da wir c herausfinden wollen, nutzen wir das Kommutativgesetz, um die Gleichung umzustellen. Jetzt setzten wir unsere bekannten Werte für a und b ein. Wir erhalten c Quadrat ist gleich 64 plus 36 also ist c Quadrat gleich 100. Um c zu berechnen, ziehen wir die Wurzel auf beiden Seiten der Gleichung. Das können wir lösen, indem wir die Zahl finden, die quadriert 100 ergibt? Die Antwort ist 10. Die Drachen müssen also nur 10 Kilometer fliegen, um zum Tempelberg zu gelangen. Diese Methode können wir nutzen, um den Abstand zwischen zwei beliebigen Punkten zu berechnen. Schauen wir die Rechnung noch mal an, um eine allgemeine Formel zu finden. Aus den Punkte B(x1 | y1) und A(x2|y2), haben wir die Länge der horizontalen Seite, also 8, durch x2 minus x1 gefunden. Die vertikale Seite des Dreiecks, also 6, fanden wir durch die Rechnung y2 minus y1. Jetzt setzen wir diese Terme in den Satz des Pythagoras ein. C bezeichnen wir mit der Variablen d, für Distanz. Wir lösen nach d, indem wir auf beiden Seiten die Wurzel ziehen. Damit erhalten wir für den Abstand d: d ist gleich die Wurzel aus in Klammern x2 minus x1 zum Quadrat plus in Klammern y2 minus y1 zum Quadrat. Wir können diese Formel benutzen, um den Abstand zwischen zwei beliebigen Punkten zu berechnen. Lass uns nun den Abstand zwischen P1(8|3) und P2(9|5) berechnen. Zuerst bezeichnen wir die Koordinaten mit x1, y1 und x2, y2. Nun setzen wir diese Werte in die Formel ein. Die Differenz der x-Koordinaten beträgt 1 und die der y-Koordinaten 2. d ist gleich der Wurzel aus 1 plus 4, also der Wurzel aus 5. Die Strecke ist also rund 2,2 Kilometer lang. Bevor die Dorfbewohner und die Drachen die große Feier starten, schauen wir uns noch einmal die Herleitung der Formel für den Abstand zweier Punkte aus dem Satz des Pythagoras an. Der Satz des Pythagoras beschreibt den Zusammenhang der Kathetenquadrate des rechtwinkligen Dreiecks zu dem Hypotenusenquadrat. Die Formel ist a Quadrat plus b Quadrat gleich c Quadrat. In einer Koordinatenebene kann der Abstand zwischen zwei Punkten durch die Hypotenuse eines rechtwinkligen Dreiecks dargestellt werden. Die Katheten des Dreiecks lassen sich berechnen als die Differenz der x-Koordinaten und der, der y-Koordinaten beider Punkte. Wir berechnen d, indem wir die Wurzel ziehen. Das ist die Formel, mit der wir den Abstand zwischen zwei beliebigen Punkten in einer Koordinatenebene finden können. Dank dieser Formel sind sowohl die Drachen, als auch die Dorfbewohner beim Tempel angekommen. Mögen die Feierlichkeiten beginnen!
Abstand zweier Punkte – Herleitung (Satz des Pythagoras) Übung
-
Berechne die gesuchten Entfernungen.
TippsDer Satz des Pythagoras besagt, dass in einem rechtwinkligen Dreieck die Summe der Katheten-Quadrate gleich dem Quadrat über der Hypotenuse ist.
Die Katheten sind diejenigen Seiten eines rechtwinkligen Dreiecks, welche den rechten Winkel bilden.
Den Satz des Pythagoras kannst du wie folgt nach der Seite $c$ umstellen:
$c=\sqrt{a^2+b^2}$.
LösungDas in dieser Aufgabe abgebildete rechtwinklige Dreieck stellt sowohl die zurückzulegende Strecke der Dorfbewohner als auch die der Drachen dar. Dabei ist uns Folgendes bekannt:
- Die Dorfbewohner gehen von $B(2\vert 1)$ über $C(10\vert 1)$ nach $A(10\vert 7)$ um den großen See herum.
- Die Drachen fliegen von $B(2\vert 1)$ nach $A(10\vert 7)$ über den See hinweg.
Strecke der Dorfbewohner
Dafür addieren wir die Katheten des rechtwinkligen Dreiecks. Kathete $a$ erhalten wir, indem wir die $x$-Koordinaten der Punkte $A$ und $B$ subtrahieren. Demnach gilt $a=10\ \text{km}-2\ \text{km}=8\ \text{km}$. Kathete $b$ erhalten wir, indem wir die $y$-Koordinaten der Punkte $A$ und $B$ subtrahieren. Somit erhalten wir $b=7\ \text{km}-1\ \text{km}=6\ \text{km}$. Die Dorfbewohner gehen also $8\ \text{km}+6\ \text{km}=14\ \text{km}$.
Strecke der Drachen
Die Berechnung der Strecke der Drachen erfolgt über den Satz des Pythagoras. Dieser besagt, dass in einem rechtwinkligen Dreieck die Summe der Katheten-Quadrate gleich dem Quadrat der Hypotenuse ist. Für das abgebildete Dreieck erhalten wir also:
$a^2+b^2=c^2$.
Die gesuchte Strecke wird durch die Hypotenuse $c$ des Dreiecks beschrieben. Wenn wir die Gleichung nach dieser umstellen, erhalten wir folgende Formel für die Berechnung des Abstands der Punkte $A$ und $B$:
$c=\sqrt{a^2+b^2}$.
Nun ersetzen wir die Katheten $a$ und $b$ mit den Koordinaten $x$ und $y$:
$c=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$.
Da wir mit dieser Formel eine Distanz berechnen möchten, ersetzen wir den Buchstaben $c$ mit einem $d$ für Distanz:
$d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$.
Jetzt können wir unsere Koordinaten einsetzen und die Strecke der Drachen berechnen:
$d=\sqrt{(10-2)^2+(7-1)^2}=\sqrt{8^2+6^2}=\sqrt{64+36}=\sqrt{100}=10$.
Die Drachen müssen also eine Strecke von nur $10\ \text{km}$ zurücklegen.
-
Gib den Abstand zwischen $P_1$ und $P_2$ an.
TippsDie Größe $d$ steht für die Distanz. Die Formel für die Berechnung der Distanz zweier Punkte wird von dem Satz des Pythagoras abgeleitet. Dieser lautet:
$\underbrace{a^2}_{\substack{\text{Kathete}}}+\underbrace{b^2}_{\substack{\text{Kathete}}}=\underbrace{c^2}_{\substack{\text{Hypotenuse}}}$.
Verwende die folgende Formel für die Berechnung des Abstands zweier Punkte $P_1(x_1\vert y_1)$ und $P_2(x_2\vert y_2)$:
$d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$.
Gesucht ist die Dezimalzahl mit einer Nachkommastelle für $\sqrt{5}$.
Nun trägst du in eine Tabelle die nächstkleinere und nächstgrößere Quadratzahl ein:
$ \begin{array}{c|c|c|c|c|c} \sqrt{4}&\sqrt{5}&\sqrt{6}&\sqrt{7}&\sqrt{8}&\sqrt{9}\\ \hline 2&&&&&3\\ \end{array} $
Fülle nun die restliche Tabelle so aus, dass von der $2$ bis zur $3$ gleichmäßige Abstände zwischen den Zahlen vorliegen.
LösungUm die Länge der Laternen-Kette zu bestimmen, muss Chang den Abstand zwischen den Punkten $P_1(8\vert 3)$ und $P_2(9\vert 5)$ ermitteln. Nun möchten wir ihm dabei helfen.
Für die Berechnung des Abstands zweier Punkte $P_1(x_1\vert y_1)$ und $P_2(x_2\vert y_2)$ benötigen wir die folgende Formel:
$d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$.
Wir setzen nun unsere Koordinaten in die Formel ein:
$d=\sqrt{(9-8)^2+(5-3)^2}=\sqrt{1^2+2^2}=\sqrt{1+4}=\sqrt{5}$.
Um dieses Ergebnis ohne Taschenrechner in eine Dezimalzahl mit einer Nachkommastelle umzurechnen, notieren wir uns eine Tabelle, in der die nächstkleinere und die nächstgrößere Quadratzahl vorkommen.
$ \begin{array}{c|c|c|c|c|c} \sqrt{4}&\sqrt{5}&\sqrt{6}&\sqrt{7}&\sqrt{8}&\sqrt{9}\\ \hline 2&&&&&3\\ \end{array} $
Wie du siehst, haben wir auch alle Wurzeln der natürlichen Zahlen zwischen $\sqrt 4$ und $\sqrt 9$ in die Tabelle aufgenommen. Die zweite Zeile der Tabelle füllen wir nun so aus, dass wir in gleichmäßigen Abständen von der $2$ zur der $3$ gelangen. Es folgt:
$ \begin{array}{c|c|c|c|c|c} \sqrt{4}&\sqrt{5}&\sqrt{6}&\sqrt{7}&\sqrt{8}&\sqrt{9}\\ \hline 2&2,2&2,4&2,6&2,8&3\\ \end{array} $
Wir erhalten somit das Ergebnis $d=2,2$.
-
Ermittle den Abstand zwischen den Punkten $A$ und $B$.
TippsDie Distanz $d$ zweier Punkte $P_1(x_1\vert y_1)$ und $P_2(x_2\vert y_2)$ kannst du mit der folgenden Formel bestimmen:
$d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$.
Im Folgenden siehst du eine Liste der Quadratzahlen von $10$ bis $20$:
$ \begin{array}{r|r|r|r|r|r|r|r|r|r} 10^2&11^2&12^2&13^2&14^2&15^2&16^2&17^2&18^2&19^2&20^2\\ \hline 100&121&144&169&196&225&256&289&324&361&400 \end{array} $
LösungIm Folgenden wird das Vorgehen bei der Berechnung der Distanz zweier Punkte am Beispiel $A(-12\vert -3)$ und $B(0 \vert -8)$ verdeutlicht.
Die Distanz $d$ zweier Punkte $P_1(x_1\vert y_1)$ und $P_2(x_2\vert y_2)$ kannst du mit der folgenden Formel bestimmen:
$d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$.
Diese wenden wir nun auf unser Beispiel an. Wir setzen die Koordinaten der Punkte $A(-12\vert -3)$ und $B(0 \vert -8)$ in die obige Formel ein und erhalten:
$d=\sqrt{(0-(-12))^2+(-8-(-3))^2}$.
Nun berechnen wir die Terme in den Klammern und quadrieren diese:
$d=\sqrt{(0-(-12))^2+(-8-(-3))^2}=\sqrt{(12)^2+(-5)^2}=\sqrt{144+25}$.
Zuletzt fassen wir die beiden Quadratzahlen zusammen und ziehen die Wurzel:
$d=\sqrt{144+25}=\sqrt{169}=13$.
Bei allen drei Beispielen resultiert eine Quadratzahl unter der Wurzel, sodass du für die Distanz $d$ eine ganze Zahl erhältst. Bei der Berechnung der Abstände der übrigen drei Beispiele gehst du genauso vor. Dann erhältst du folgende Ergebnisse:
Abstand der Punkte $A(-3\vert 2)$ und $B(-7 \vert -1)$
$d=\sqrt{(-7-(-3))^2+(-1-2)^2}=\sqrt{(-4)^2+(-3)^2}=\sqrt{16+9}=\sqrt{25}=5$
Abstand der Punkte $A(-3\vert 3)$ und $B(-9 \vert -5)$
$d=\sqrt{(-9-(-3))^2+(-5-3)^2}=\sqrt{(-6)^2+(-8)^2}=\sqrt{36+64}=\sqrt{100}=10$
Abstand der Punkte $A(-6\vert 8)$ und $B(6\vert -8)$
$d=\sqrt{(6-(-6))^2+(-8-8)^2}=\sqrt{(12)^2+(-16)^2}=\sqrt{144+256}=\sqrt{400}=20$
-
Bestimme die Distanz zwischen den Fußballspielern Luke und Max.
TippsGesucht ist der Abstand zwischen den Punkten $L(10\vert 5)$ und $M(14\vert 8)$. Verwende hierzu die Formel $d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$.
Du quadrierst eine Zahl, indem du diese Zahl einmal mit sich selbst multiplizierst:
$5^2=5\cdot 5=25$.
Die $25$ ist eine Quadratzahl. Ziehst du die Wurzel einer Quadratzahl, so erhältst du eine ganze Zahl.
LösungFolgende Spielerpositionen sind uns bekannt:
- Luke $L(10\vert 5)$
- Max $M(14\vert 8)$
- Tobi $T(12\vert 5)$
Wir setzen die Koordinaten ein und rechnen:
$d=\sqrt{(14-10)^2+(8-5)^2}=\sqrt{(4)^2+(3)^2}=\sqrt{16+9}=\sqrt{25}=5$.
Luke muss also $5\ \text{m}$ weit schießen.
-
Gib die Formeln für die Berechnung des Abstands zweier Punkte an.
TippsDie Formel, mit der der Abstand zwischen zwei Punkten berechnet werden kann, wird von dem Satz des Pythagoras abgeleitet. Dieser lautet:
$\underbrace{a^2}_{\substack{\text{Kathete}}}+\underbrace{b^2}_{\substack{\text{Kathete}}}=\underbrace{c^2}_{\substack{\text{Hypotenuse}}}$.
Dabei entspricht die Hypotenuse der gesuchten Distanz $d$.
Gegeben sind die Punkte $A(1\vert 5)$ und $B(4\vert 2)$. Nun betrachten wir das Quadrat der Differenz der $x$-Koordinaten:
- $(x_1-x_2)^2=(1-4)^2=(-3)^2=-3\cdot (-3)=9$
- $(x_2-x_1)^2=(4-1)^2=(3)^2=3\cdot 3=9$
LösungDie Formel für die Berechnung der Distanz $d$ zweier Punkte $P_1(x_1\vert y_1)$ und $P_2(x_2\vert y_2)$ wird von dem Satz des Pythagoras abgeleitet. Dieser lautet:
$\underbrace{a^2}_{\substack{\text{Kathete}}}+\underbrace{b^2}_{\substack{\text{Kathete}}}=\underbrace{c^2}_{\substack{\text{Hypotenuse}}}$.
Dabei entspricht die Hypotenuse $c$ der gesuchten Distanz $d$. Also ersetzen wir nun $c$ durch $d$ und vertauschen die Seiten der Gleichung.
$d^2=a^2+b^2$
Die Katheten $a$ und $b$ kannst du über die Differenz der $x$- und $y$-Koordinaten bestimmen. Es folgt:
$d^2=(x_2-x_1)^2+(y_2-y_1)^2$.
Mit dieser Formel kannst du bereits den Abstand zwischen zwei Punkten berechnen. Wir können diese aber auch noch weiter umformen.
Da die Differenzen quadriert werden, spielt die Reihenfolge der Subtraktion keine Rolle. Daher können wir die Katheten ebenfalls durch folgende Differenzen ersetzen:
$d^2=(x_1-x_2)^2+(y_1-y_2)^2$.
Abschließend wird auf beiden Seiten der Gleichung die Wurzel gezogen, sodass wir eine Formel für die Distanz $d$ erhalten:
$d=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}$.
-
Ermittle die Länge des benötigten Seils.
TippsDu kannst dir die Formel für die Distanz aus dem Satz des Pythagoras herleiten:
$a^2+b^2=c^2$.
Die Koordinaten des Punktes $P_2$ sind gegeben durch $P_2(70\vert 95)$.
Die horizontale Entfernung entspricht der Distanz entlang der $x$-Achse und die vertikale Entfernung entlang der $y$-Achse.
LösungGesucht ist die Länge eines Seils, welches vom Punkt $P_1(10\vert 15)$ bis zu dem Punkt $P_2$ reichen soll.
Uns ist bekannt, dass der Punkt $P_2$ eine horizontale Entfernung von $60\ \text{m}$ und eine vertikale Entfernung von $80\ \text{m}$ zum Punkt $P_1$ hat.
Demnach erhalten wir die folgenden Koordinaten für den Punkt $P_2$:
$P_2(10+60\vert 15+80)$ also $P_2(70\vert 95)$.
Mit diesen beiden Punkten und der Formel $d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$ können wir nun ermitteln, wie lang Thorsten das Seil wählen muss. Bei unseren Koordinaten entspricht eine Einheit einem Meter. Wir rechnen:
$d=\sqrt{(70-10)^2+(95-15)^2}=\sqrt{(60)^2+(80)^2}$.
Wie du bereits erkennen kannst, erhalten wir für die Differenzen in den Klammern die horizontale und vertikale Entfernung. Genau diese werden nämlich durch die beiden Katheten des rechtwinkligen Dreiecks, welches wir bei der Abstandsberechnung betrachten, beschrieben. Wir hätten uns also auch das Aufstellen des Punktes $P_2$ sparen und direkt mit den gegebenen Distanzen rechnen können. Nun weiter in unserer Rechnung:
$d=\sqrt{(60)^2+(80)^2}=\sqrt{3~600+6~400}=\sqrt{10~000}=100$.
Thorsten benötigt für sein Bauprojekt also ein Seil mit einer Länge von $100\ \text{m}$.
9.966
sofaheld-Level
6.600
vorgefertigte
Vokabeln
8.314
Lernvideos
38.641
Übungen
33.706
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Klassenstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung




 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?















Echt gut erklärt .
Super 👍🏻
super
gut:/
Danke, Das Video ist gut erklät