Abstand zweier Punkte berechnen
Zur Berechnung des Abstands zwischen zwei Punkten wird die euklidische Distanz verwendet, die sich aus der Länge der Strecke zwischen ihnen ergibt. Der Satz des Pythagoras wird genutzt, um die Koordinatenunterschiede in einem rechtwinkligen Dreieck zu berechnen. Möchtest du mehr darüber erfahren und üben, wie man den Abstand wie Carlos bestimmt? Interessiert? Dann lies weiter in dem folgenden Text.
in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
5 Minuten verstehen
5 Minuten üben
2 Minuten Fragen stellen
Bereit für eine echte Prüfung?
Grundlagen zum Thema Abstand zweier Punkte berechnen
Einführung: Was ist der Abstand zwischen zwei Punkten?
Carlos Schulweg führt um eine Schlucht herum. Er möchte gern eine Abkürzung konstruieren: eine Seilbahnrutsche direkt über die Schlucht hinweg. Wird die Wäscheleine seiner Mutter dafür reichen? Um das herauszufinden, muss Carlos wissen, wie lang die Strecke von zu Hause bis zur Schule auf direktem Weg ist. Die Strecke ist genau dasselbe wie der Abstand zwischen den beiden Punkten, an denen sich sein Zuhause und seine Schule befinden. In diesem Text und Video wird dir verständlich erklärt, wie man den Abstand zweier Punkte im Koordinatensystem berechnet.
Distanz zwischen zwei Punkten – Definition
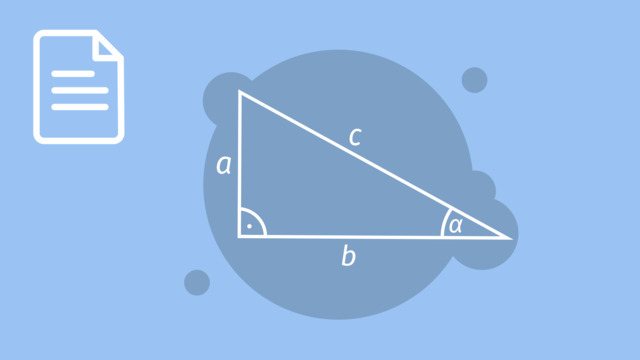
Der Abstand zweier Punkte ist die Länge der Strecke, die diese beiden Punkte verbindet. Den Abstand nennt man auch euklidischen Abstand oder euklidische Distanz. Wir betrachten die beiden Punkte $P_1(x_1|y_1)$ und $P_2(x_2|y_2)$ im Koordinatensystem. Um ihren Abstand zu berechnen, nehmen wir ein rechtwinkliges Dreieck zu Hilfe.
Die Hypotenuse $c$ des Dreiecks ist die gesuchte Strecke. Wir nutzen den Satz des Pythagoras, um die Strecke zu berechnen:
$a^{2}+b^{2} = c^{2}$
Die beiden Katheten $a$ und $b$ liegen parallel zur $x$-Achse sowie zur $y$-Achse des Koordinatensystems. Die Strecke $a$ ersetzen wir durch $(x_2-x_1)$, denn sie ist genauso lang wie die Differenz der $x$-Koordinaten. Analog ersetzen wir $b$ durch $(y_2-y_1)$. Setzen wir diese Terme in den Satz des Pythagoras ein, so erhalten wir:
$(x_2-x_1)^{2} + (y_2-y_1)^{2} = c^{2}$
Statt $c$ wie im Satz des Pythagoras schreiben wir für den Abstand die Variable $d$, denn der Abstand heißt auch Distanz. Den Wert von $d$ erhalten wir also, indem wir aus $c^{2}$ die Wurzel ziehen:
$d = \sqrt{(x_2-x_1)^{2} + (y_2-y_1)^{2}}$
Wie berechnet man den Abstand zweier Punkte im Koordinatensystem?
Wir schauen uns an, wie wir die Formel für die Distanz anwenden: Carlos Hütte hat die Koordinaten $P_1(100|100)$, seine Schule hat die Koordinaten $P_2(200|400)$.
Wir berechnen die Differenzen der Koordinaten:
$(x_2-x_1) = (200-100) = 100 \newline (y_2-y_1) = (400-100) = 300$
Nun quadrieren wir diese Zahlen und addieren sie:
$100^{2} + 300^{2} = 10\,000 + 90\,000 = 100\,000$
Nun ziehen wir daraus die Wurzel:
$d= \sqrt{100\,000} \approx 316,23$
Der Abstand der beiden Punkte beträgt also $316,23~\pu{m}$. Die Wäscheleine von Carlos Mutter ist etwa $350~\pu{m}$ lang – das genügt also, um die Schlucht mit einer Seilbahnrutsche zu überwinden. Aber ob die Wäscheleine auch hält? Diese Frage hängt nicht vom Abstand ab.
Zusammenfassung: Abstand zweier Punkte berechnen
Die folgenden Stichpunkte fassen dabei noch einmal das Wichtigste zum Thema Abstand zweier Punkte berechnen zusammen.
- Der (euklidische) Abstand zweier Punkte ist die Länge der Strecke, die diese beiden Punkte verbindet.
- Um den Abstand zu berechnen, nehmen wir ein rechtwinkliges Dreieck zu Hilfe.
- Der Satz des Pythagoras ermöglicht uns eine Berechnung des Abstands der beiden Punkte (Hypotenuse) mithilfe der beiden anderen Seiten des rechtwinkligen Dreiecks (Katheten).
Weitere Übungen und Aufgaben zum Thema Abstand zweier Punkte berechnen findest du hier bei sofatutor.
Transkript Abstand zweier Punkte berechnen
Tief im Amazonas-Regenwald lebt Carlos mit seiner Familie in einem winzigen Dorf. Carlos liebt fast alles am Dorfleben, aber er muss schon bei Tagesanbruch aufstehen, um rechtzeitig zur Schule zu kommen. Eigentlich ist die Schule gar nicht so weit vom Dorf entfernt, aber dazwischen liegt eine weite Schlucht, um die Carlos herumlaufen muss. Darum hat er einen Plan entwickelt, um schneller zur Schule zu kommen. Aber um sicherzugehen, dass der Plan auch funktioniert muss er den Abstand von zwei Punkten berechnen. Schauen wir uns die Karte an. Die Einheiten sind in Metern angegeben. Dies ist Carlos Schulweg. Hier an der Schlucht entlang, über die Brücke, und dann auf der anderen Seite die Schlucht entlang. Für den Weg braucht Carlos jeden Tag fast 2 Stunden. Welchen großartigen Plan hat Carlos also? Er möchte eine Seilrutsche über die Schlucht bauen, um in einem Bruchteil der Zeit zur Schule zu kommen. Aber er hat kein Seil. Was kann er also tun? Er hat einen genialen Einfall: Er wird einfach die Wäscheleine seiner Mutter benutzen. Die Sache hat aber zwei Haken: Die Wäscheleine ist nur 350 Meter lang. Wird das reichen? Und was wird seine Mutter dazu sagen, dass er ihre Wäscheleine so zweckentfremdet? Um die erste Frage zu beantworten, muss er den Abstand zwischen diesen beiden Punkten berechnen. Und was seine Mutter angeht: Das wird die Zeit zeigen. Mit seiner Mutter können wir ihm nicht helfen, mit dem mathematischen Problem aber schon. Um den Abstand zwischen zwei bekannten Punkten zu berechnen, nehmen wir ein rechtwinkliges Dreieck zur Hilfe. Wir nutzen den Satz des Pythagoras, um die gesuchte Strecke zu berechnen. Beachte, wie wir a und b durch x2minus x1 beziehungsweise y2minus y1 ersetzt haben. Da c die Distanz, also der Abstand, zwischen den beiden Punkten ist, nennen wir die Variable nun d. Nachdem wir auf beiden Seiten die Wurzel gezogen haben, erhalten wir die Formel, um den Abstand zu berechnen. Carlos' Dorf ist im Punkt P1(100|100). Und die Schule ist beim Punkt P2 (200|400). Da wir die Punkte kennen, können wir die Variablen in der Formel ersetzen und den Abstand berechnen. "Das können wir jetzt mit ein paar Rechenoperationen ganz einfach lösen. Die Seilrutsche muss etwa 316,23 Meter lang sein. Carlos' Seil ist also lang genug." Er ist ganz aufgeregt, die Seilrutsche das erste Mal zu benutzen. Und er konnte sogar fast 2 Stunden länger als sonst schlafen. Und los geht's. Wuhu! Oh Mann. Jetzt weiß Carlos über die Dorfbewohner mehr, als ihm lieb ist.
Abstand zweier Punkte berechnen Übung
-
Gib die Schrittfolge bei der Berechnung des Abstandes zweier Punkte wieder.
TippsSetze in die Abstandsformel die Zahlen ein und löse die Gleichung.
Die erste Formel lautet:
$d=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}$
Setze hier die Werte ein und rechne die Gleichung aus.
LösungDie Ausgangsgleichung folgt aus dem Satz des Pythagoras:
$d=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}$
Zuerst setzt du die Werte aus der Skizze ein:
$d=\sqrt{(200-100)^{2}+(400-100)^{2}}$
Nun rechnest du die Differenzen in den Klammern aus:
$d=\sqrt{(100)^{2}+(300)^{2}}$
Danach bildest du die Quadrate:
$d=\sqrt{10 000+90 000}$
Fasse die Summe zusammen:
$d=\sqrt{100 000}$
Wenn du jetzt noch die Wurzel ziehst, erhältst du das Ergebnis:
$d\approx316,23$
Da die Wäscheleine von Carlos Mutter $350~$m lang ist, reicht sie für die Strecke völlig aus.
-
Gib an, wie du vom Satz des Pythagoras zur Abstandsformel kommst.
TippsDie Hypothenuse $c$ entspricht dem Abstand $d$ der zwei Punkte.
$d$ steht für „distance“. Das ist Englisch und bedeutet „Abstand“.Achtung: Die Summe zweier Wurzeln ist normalerweise etwas anderes als die Wurzel einer Summe.
Beispiel:
- $\sqrt{36}+\sqrt{64}=6+8=14$
- $\sqrt{36+64}=\sqrt{100}=10$
LösungBetrachtest du die Skizze, erkennst du ein rechtwinkliges Dreieck. Die beiden Katheten $a$ und $b$ entsprechen den Differenzen der $x$-Werte und $y$-Werte beider Punkte:
$x_{2}-x_{1}$ und $y_{2}-y_{1}$
Der Abstand $d$ beider Punkte wird durch die Hypotenuse $c$ des Dreiecks gebildet.
Der Satz des Pythagoras lautet:
$a^2+b^2=c^2$
Er wird durch den folgenden Ausdruck ersetzt:
$(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}=d^{2}$
Wir wollen den Abstand ermitteln, also wird auf beiden Seiten die Wurzel gezogen:
$d=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}$
-
Vergleiche die Lösungswege zur Berechnung der Abstände verschiedener Punktepaare.
TippsTrage die gegebenen Punkte zunächst in ein Koordinatensystem ein und überlege dir, wie groß die Differenzen zwischen den $x$-Werten bzw. die Differenzen zwischen den $y$-Werten sind.
Die Punkte, zwischen denen jeweils der Abstand gesucht ist, stehen hier untereinander. Subtrahiere bei den Angaben zu den Punkten die untereinander stehenden Zahlen, weil in der Abstandsformel $x_{2}-x_{1}$ bzw. $y_{2}-y_{1}$ stehen und nicht $x_{1}-y_{1}$ bzw. $x_{2}-y_{2}$. Schaue, ob du die Ergebnisse in den Gleichungen wiederfindest.
Der Abstand $d$ zwischen $P_{1}$ und $P_{2}$ beträgt $5$.
Der Abstand zwischen $Q_{1}$ und $Q_{2}$ beträgt $10$.
Der Abstand zwischen $R_{1}$ und $R_{2}$ beträgt $13$.LösungBei der Berechnung des Abstandes zwischen zwei Punkten wird diese Abstandsformel angewendet:
$d=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}$
1. Punktepaar: $P_{1}$ und $P_{2}$
- Für $P_{1}$ und $P_{2}$ sind $x_{1}=3$ und $x_{2}=6$, die Differenz ist dann $x_{2}-x_{1}=6-3=3$.
- Für $P_{1}$ und $P_{2}$ sind $y_{1}=5$ und $y_{2}=9$, die Differenz ist dann $y_{2}-y_{1}=9-5=4$.
Eingesetzt in obige Formel für den Satz des Pythagoras ergibt das:
$d=\sqrt{(6-3)^{2}+(9-5)^{2}}$
$d=\sqrt{(3)^{2}+(4)^{2}}$
$d=\sqrt{9+16}=\sqrt{25}$
$d=5$
2. Punktepaar: $Q_{1}$ und $Q_{2}$
- Für $Q_{1}$ und $Q_{2}$ sind $x_{1}=1$ und $x_{2}=6$, die Differenz ist dann $x_{2}-x_{1}=6-1=5$.
- Für $Q_{1}$ und $Q_{2}$ sind $y_{1}=2$ und $y_{2}=14$, die Differenz ist dann $y_{2}-y_{1}=14-2=12$.
Eingesetzt in die obige Formel für den Satz des Pythagoras ergibt das:
$d=\sqrt{(6-1)^{2}+(14-2)^{2}}$
$d=\sqrt{(5)^{2}+(12)^{2}}$
$d=\sqrt{25+144}=\sqrt{169}$
$d=13$
3. Punktepaar: $R_{1}$ und $R_{2}$
- Für $R_{1}$ und $R_{2}$ sind $x_{1}=0$ und $x_{2}=6$, die Differenz ist dann $x_{2}-x_{1}=6-0=6$.
- Für $R_{1}$ und $R_{2}$ sind $y_{1}=6$ und $y_{2}=14$, die Differenz ist dann $y_{2}-y_{1}=14-6=8$.
Eingesetzt in die obige Formel für den Satz des Pythagoras ergibt das:
$d=\sqrt{(6-0)^{2}+(14-6)^{2}}$
$d=\sqrt{(6)^{2}+(8)^{2}}$
$d=\sqrt{36+64}=\sqrt{100}$
$d=10$
-
Bestimme den Abstand der Punkte $S(12\vert99)$ und $T(51\vert19)$.
TippsDie Bezeichnung $\vert \overline{ST} \vert$ ist nur eine andere Bezeichnung für den Abstand zwischen den Punkten $S$ und $T$. Häufig wird dieser auch mit $d$ bezeichnet.
Der Betrag gibt immer den positiven Wert einer Zahl aus:
$\vert4\vert=4$ und $\vert-4\vert=4$
LösungDie Koordinaten des Punktes $S$ sind:
$x_{S}=12$ und $y_{S}=99$
Die Koordinaten des Punktes $T$ sind:
$x_{T}=51$ und $y_{T}=19$
Weil hier mit Abständen gerechnet wird, kannst du positive Zahlen verwenden. Rechne also erst die Differenz aus und nimm anschließend den Betrag:
$\vert x_{S}-x_{T} \vert =\vert 12-51\vert=\vert -39\vert=39$ und $\vert y_{S}-y_{T} \vert =\vert 99-19\vert=\vert80\vert=80$
Für den Abstand $\overline{ST}$ zwischen den Punkten $S$ und $T$ folgt dann mit der Abstandsformel:
$\vert \overline{ST} \vert^{2}=(x_{S}-x_{T})^{2}+(y_{S}-y_{T})^{2}=39^2+80^2=1 521+6 400=7 921$
Daraus ziehst du noch die Wurzel:
$\vert \overline{ST} \vert=89$.
-
Nenne wichtige Angaben für die Abstandsberechnung zweier Punkte.
TippsDas ist die Formel zur Abstandsberechnung:
$d=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}$
Sieh sie dir genau an und überlege, welche Werte alle bekannt sein müssen, um sie anzuwenden.
LösungÜberlege dir anhand der konkreten Berechnung des Abstandes, welche Angaben zu den Punkten du brauchst: In der Formel tauchen die $x$-Werte und die $y$-Werte von zwei Punkten auf. Das ist die Formel für den Abstand:
$d=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}$
Also gilt Folgendes für die einzelnen Aussagen:
- Es müssen zwei Punkte gegeben sein. Mit nur einem Punkt lässt sich kein Abstand berechnen.
- Es genügt, wenn du für beide Punkte entweder die x-Werte oder die y-Werte kennst.
- Es genügt, wenn du die Koordinaten eines Punktes kennst. Die Koordinaten des anderen Punktes ergeben sich dann.
- Für beide Punkte brauchst du die $x$-Werte und die $y$-Werte.
-
Bestimme den Abstand zwischen der Schule und der Musikschule.
TippsTrage beide Punkte in ein Koordinatensystem ein: Sowohl die Schule als auch die Musikschule liegen östlich und nördlich des Wohnhauses von Mia und Sophia. Sie liegen also im selben Quadranten des Koordinatensystems. Da der Punkt $S$ für die Schule vorgegeben ist, sind die Koordinaten des Punktes $M$ für die Musikschule festgelegt.
LösungDie Koordinaten
Die Koordinaten der Punkte ergeben sich genau aus den Angaben. Vorgegeben ist der Punkt $S(250\vert150)$. Alle Angaben sind positiv. Da Schule und Musikschule beide östlich und nördlich vom Koordinatenursprung (dem Wohnhaus von Mia und Sophia) liegen, befinden sie sich im gleichen Quadranten des Koordinatensystems. Der Punkt $M$ hat also die gleichen Vorzeichen wie der Punkt $S$:
$x_{M}=450$ und $y_{S}=600$
Der Fußweg
Ein Fußgänger bzw. eine Fußgängerin kann sich nur entlang der Straßenzüge in Ost-West-Richtung bzw. Nord-Süd-Richtung bewegen. Die Wegstrecken entsprechen daher genau den Differenzen der $x$- bzw. $y$-Werte der Koordinaten. Da aber Streckenlängen stets positiv sind, rechnest du mit den Beträgen der Differenzen:
$\vert x_{M}-x_{S}\vert=200$ und $\vert y_{M}-y_{S}\vert=450$
Diese beiden Werte müssen nun addiert werden, um den Gesamtweg auszurechnen:
$\vert x_{M}-x_{S}\vert+\vert y_{M}-y_{S}\vert=200+450=650$
Der Fußweg zwischen Schule und Musikschule ist $650$ m lang.
Die Luftlinien-Entfernung
Um die wirkliche Entfernung zwischen Schule und Musikschule auszurechnen, verwendest du wieder den Satz des Pythagoras, der in dieser Aufgabe folgendermaßen aussieht:
$\overline{MS}^2=(x_{M}-x_{S})^2+(y_{M}-y_{S})^2$
Setzen wir hier die oben ausgerechneten Beträge der Differenzen ein, ergibt sich:
$\overline{MS}^2=200^2+450^2$
Rechne die Quadrate aus und bilde die Summe:
$\overline{MS}^2=40 000+202 500=242 500$
Daraus ziehst du noch die Wurzel:
$\overline{MS}\approx492,44$
Die Schule und die Musikschule sind etwa $492,44~$m voneinander entfernt.
8.905
sofaheld-Level
6.601
vorgefertigte
Vokabeln
7.695
Lernvideos
37.343
Übungen
33.674
Arbeitsblätter
24h
Hilfe von Lehrkräften
Inhalte für alle Fächer und Klassenstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebeziehungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Quadrat
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Was Ist Eine Viertelstunde
- Prisma
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Satz Des Pythagoras
- Dreieck Grundschule
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Zahlen In Worten Schreiben
- Meter
- Orthogonalität
- Schriftlich Multiplizieren
- Brüche gleichnamig machen
- Brüche Multiplizieren
- Potenzgesetze
- Distributivgesetz
- Bruchgleichungen lösen – Übungen
- Flächeninhalt Dreieck
- Rationale Zahlen
- Volumen Berechnen
Belohnend alla
schlaue leute da xD
warum bauen die die schule nicht im Dorf ? die sind nicht so schlau Alla
Belohnende SAche Allllllla
Hallo Bonnypreikschas, du hast recht, man kann die Wurzel auch direkt aus 100.000 ziehen, besonders, wenn man mit dem Taschenrechner rechnet. Das Verfahren, was hier angewendet wurde, nennt sich teilweises Wurzelziehen. Tatsächlich lassen sich kleinere Wurzeln nämlich leichter abschätzen als große. Da die 10 zwischen 9=3² und 16=4² liegt, wissen wir, dass die Wurzel aus 10 zwischen 3 und 4 liegt und zwar deutlich näher an der 3. Eine solche Abschätzung ist für die 100.000 viel schwerer möglich.
Ich hoffe, dass wir Dir weiterhelfen können.
Viele Grüße aus der Redaktion.