Satz des Pythagoras – Beweis
Tauche ein in die Welt des Pythagoras! Erfahre, wie seine Formel $a^{2}+b^{2}=c^{2}$ in jedem rechtwinkligen Dreieck Anwendung findet. Erhalte Einblicke in geometrische Beweise und vertiefe dein Verständnis durch interaktive Übungen und Arbeitsblätter. All das und mehr erwartet dich im Video! Interessiert? Dann lies weiter und werde selbst zum Pythagoras-Experten!


in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.

Grundlagen zum Thema Satz des Pythagoras – Beweis
Satz des Pythagoras
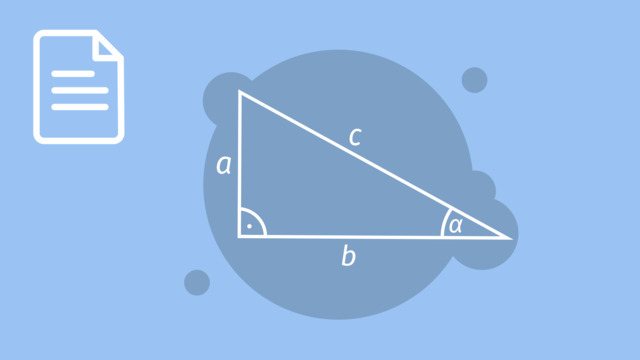
Der Satz des Pythagoras besagt: Bei einem rechtwinkligen Dreieck ist die Summe der beiden Kathetenquadrate genau gleich dem Hypotenusenquadrat. Das schreibt man meistens als Formel auf. Die beiden Katheten werden mit $a$ und $b$ bezeichnet, die Hypotenuse mit $c$. Der Satz des Pythagoras kann damit durch die folgende Formel ausgedrückt werden:
$a^{2}+b^{2}=c^{2}$
In diesem Video wird dir ein Beweis dieses Satzes verständlich erklärt. Der Beweis des Satzes stellt sicher, dass der Satz für beliebige rechtwinklige Dreiecke gilt.
Satz des Pythagoras – geometrischer Beweis
Mit geeigneten Bauklötzen in der Form kongruenter rechtwinkliger Dreiecke sowie einem Quadrat der passenden Größe kannst du die folgende Figur zusammensetzen:
Die Kantenlänge des kleinen Quadrats im Inneren der Figur entspricht der Hypotenuse des rechtwinkligen Dreiecks, also $c$. Die beiden Katheten $a$ und $b$ ergeben nebeneinandergelegt die Seitenlänge $(a+b)$ des äußeren Quadrats. Wir berechnen den Flächeninhalt $A_{\Box}$ des äußeren Quadrats:
$A_{\Box} = (a+b)^{2} = a^{2}+2ab+b^{2}$
In der rechten Gleichung haben wir die binomische Formel verwendet.
Da sich das äußere Quadrat aus den vier kongruenten Dreiecken und dem inneren Quadrat zusammensetzt, können wir seinen Flächeninhalt auch durch die Flächeninhalte dieser einzelnen Figuren beschreiben. Den Flächeninhalt jedes der rechtwinkligen Dreiecke können wir mit der Formel $A_\Delta = \frac{1}{2}gh$ berechnen. Hierbei ist $g$ die Grundseite und $h$ die zugehörige Höhe des Dreiecks. Bei einem rechtwinkligen Dreieck können wir $g=a$ und $h=b$ wählen – oder umgekehrt. Der Flächeninhalt jedes der rechtwinkligen Dreiecke ist also:
$A_\Delta = \frac{1}{2} \cdot a \cdot b$
Bevor wir den Flächeninhalt des inneren Quadrats bestimmen, stellen wir sicher, dass die Figur im Inneren wirklich ein Quadrat ist. Da die vier Dreiecke, die an den Seiten dieser inneren Figur anliegen, zueinander kongruent sind, haben alle vier Seiten der inneren Figur dieselbe Seitenlänge, nämlich $c$. Ein Viereck mit vier gleich langen Seite nennt man Raute. Ein Quadrat ist eine sehr spezielle Raute, bei der nämlich alle Innenwinkel dieselbe Winkelgröße von $90^\circ$ haben. Die Winkelgröße des Innenwinkels der inneren Figur können wir mithilfe der Winkelsumme im Dreieck herausfinden.
In dem rechtwinkligen Dreieck beträgt die Summe der Winkel $\alpha+\beta=90^\circ$. An dem gestreckten Winkel, der einem Eckpunkt des inneren Vierecks anliegt, ergeben sich ebenfalls die Winkel $\alpha$ und $\beta$.
Der Innenwinkel $\delta$ des inneren Vierecks bildet zusammen mit den Winkeln $\alpha$ und $\beta$ einen gestreckten Winkel.
Nun können wir die Winkelgröße des Innenwinkels $\delta$ ausrechnen. Für den gestreckten Winkel erhalten wir:
$180^\circ = \alpha+\beta+\delta$
Lösen wir die Gleichung nach $\delta$ auf, so erhalten wir für jeden Innenwinkel des inneren Vierecks:
$\delta = 90^\circ$
Das innere Viereck hat demnach vier gleich lange Seiten und seine Innenwinkel sind rechte Winkel. Das Viereck ist also ein Quadrat. Sein Flächeninhalt beträgt $c^{2}$, denn seine Seitenlänge ist $c$.
Setzen wir den Flächeninhalt $A_{\Box}$ des äußeren Quadrats mit der Summe der Flächeninhalte der einzelnen Figuren gleich, so erhalten wir:
$A_{\Box} = 4 \cdot A_{\Delta} + c^{2}$
Nun setzen wir $A_{\Box} = a^{2}+2ab+b^{2}$ ein und erhalten:
$a^{2}+2ab+b^{2} = 4 \cdot \frac{1}{2}ab + c^{2} = 2ab+c^{2}$
Wir subtrahieren auf beiden Seiten $2ab$ und erhalten die Formel aus dem Satz des Pythagoras:
$a^{2}+b^{2}=c^{2}$
Satz des Pythagoras - Zusammenfassung
In diesem Video wird dir ein geometrischer Beweis des Satzes des Pythagoras verständlich erklärt. Mit diesem Beweis kannst du begründen, dass der Satz des Pythagoras für alle rechtwinkligen Dreiecke gilt. Zu diesem Video gibt es interaktive Übungen und ein Arbeitsblatt, sodass du dein neues Wissen sofort ausprobieren kannst.
Transkript Satz des Pythagoras – Beweis
Moritz sitzt gerade an seinen Hausaufgaben zum Satz des Pythagoras und beobachtet seine kleine Schwester Sina, als plötzlich Heureka! Die Anordnung von Sinas Bauklötzen inspiriert Moritz zu einem Beweis für den Satz des Pythagoras. Wenn wir beweisen, dass der Satz des Pythagoras für ein rechtwinkliges Dreieck mit beliebig langen Seiten gilt, dann gilt er für alle rechtwinkligen Dreiecke. Du erinnerst dich: Der Satz des Pythagoras besagt, dass bei einem rechtwinkligen Dreieck die Summe der beiden Kathetenquadrate dem Hypotenusenquadrat entspricht. Mit Variablen schreiben wir das als 'a' Quadrat plus 'b' Quadrat gleich 'c' Quadrat. Diesen Satz wollen wir, mit ein bisschen Logik und bekannten Gesetzen, beweisen. Wenn wir den Satz des Pythagoras erst einmal bewiesen haben, können wir mit ihm unbekannte Seitenlängen berechnen. Schau mal: Sinas Klötze bilden ein großes Quadrat, das aus 4 rechtwinkligen Dreiecken zusammengesetzt ist, und ein kleineres Quadrat. Jede Seite des großen Quadrats setzt sich zusammen aus den Längen 'a' und 'b'. Um den Satz des Pythagoras zu beweisen, werden wir den Flächeninhalt des großen Quadrates mithilfe seiner Seitenlängen berechnen. Danach können wir ihn mit dem Flächeninhalt der Figuren, aus denen das Quadrat besteht, gleichsetzen. Du weißt ja, den Flächeninhalt eines Quadrats berechnet man, indem man seine Seitenlänge quadriert. Welche Seitenlänge hat das große Quadrat? a plus b. Das Quadrat hat also eine Fläche von Klammer auf, 'a' plus 'b', Klammer zu, zum Quadrat. Wenn man etwas quadriert, dann multipliziert man es mit sich selbst. Unsere Rechnung bedeutet also lediglich: In Klammern 'a' plus 'b' mal in Klammern 'a' plus 'b'. Hast du bemerkt, dass wir hier zwei Binome multiplizieren? Wir benutzen also die 1. binomische Formel: (a+b) zum Quadrat ist gleich a Quadrat plus 2 ab plus b Quadrat. Die Fläche des großen Quadrats ist also gleich 'a' Quadrat plus '2ab' plus 'b' Quadrat. Die gleiche Fläche muss herauskommen, wenn wir die Flächen der Dreiecke und des kleinen Quadrats addieren. Bestimmen wir also zuerst die Fläche der Dreiecke. Sind diese Dreiecke kongruent? Wenn wir sie übereinanderlegen, sehen wir, dass sie tatsächlich deckungsgleich sind. Wir müssen also nur die Fläche eines Dreiecks berechnen. Wie war nochmal die Formel für den Flächeninhalt eines Dreiecks? Einhalb Grundseite mal Höhe. Für die Grundseite können wir 'a' einsetzen und für die Höhe 'b'. So erhalten wir einhalb 'ab'. Das ist die Fläche für EINS der Dreiecke; für alle vier lautet sie also: 4 mal einhalb 'ab'. Wir vereinfachen das und erhalten für die Fläche der vier Dreiecke: '2ab'. Widmen wir uns nun dem kleinen Quadrat. Woher wissen wir denn eigentlich, dass das auch wirklich ein Quadrat ist? Wenn eine Figur vier gleichlange Seiten und vier rechte Winkel besitzt, ist sie ein Quadrat. Da die vier Dreiecke kongruent sind, sind auch diese vier Seiten hier gleich lang. Wir nennen diese Seiten 'c'. Okay, das Viereck hat also vier gleichlange Seiten, aber wie sieht es mit den rechten Winkeln aus? Um diese Winkel zu bestimmen, erinnern wir uns an die Regel für die Winkelsumme in einem Dreieck, die besagt, dass die Innenwinkel eines Dreiecks zusammen 180 Grad ergeben. Da wir bereits wissen, dass das Dreieck einen Winkel von 90 Grad besitzt, müssen diese beiden spitzen Winkel hier zusammen 90 Grad groß sein. Da die Dreiecke kongruent sind, müssen ihre entsprechenden Winkel gleich sein. Deswegen ergeben diese beiden Winkel addiert ebenfalls 90 Grad. Und da das hier ein gestreckter Winkel von 180 Grad ist, muss dieser Winkel hier aus der inneren Figur also 90 Grad groß sein. Die innere Figur besitzt 4 rechte Winkel, also handelt es sich dabei tatsächlich um ein Quadrat. Demnach können wir den Flächeninhalt ganz flink berechnen, indem wir die Seitenlänge quadrieren. Die Seitenlänge ist 'c', der Flächeninhalt also 'c' Quadrat. Du erinnerst dich, dass die Fläche des großen Quadrats gleich der Fläche der vier Dreiecke plus der Fläche des kleinen Quadrats ist. Die Fläche des großen Quadrats ist 'a' Quadrat plus '2ab' plus 'b' Quadrat. Die Fläche der vier Dreiecke ist '2ab' und die des kleinen Quadrats ist 'c' Quadrat. Schau mal, '2ab' taucht auf beiden Seiten der Gleichung auf. Wir können also auf beiden Seiten '2ab' subtrahieren. Übrig bleibt 'a' Quadrat plus 'b' Quadrat gleich 'c' Quadrat. a und b sind die Katheten eines rechtwinkligen Dreiecks und c seine Hypotenuse. Das beweist, dass der Satz des Pythagoras für ALLE rechtwinkligen Dreiecke gilt. Fassen wir den Beweis noch mal zusammen. Am Anfang hatten wir eine Figur aus einem kleineren Quadrat in einem größeren. Wir haben den Flächeninhalt des großen Quadrats berechnet und ihn gleichgesetzt mit der Summe der Flächen der Figuren, aus denen es zusammengesetzt ist. So haben wir die Gleichung 'a' Quadrat plus 'b' Quadrat gleich 'c' Quadrat erhalten. Dadurch können wir sicher sein, dass der Satz des Pythagoras für alle rechtwinkligen Dreiecke gilt. Mit dem Satz des Pythagoras kann man die Länge einer Seite eines rechtwinkligen Dreiecks berechnen, wenn man die beiden anderen Seitenlängen kennt. Ob Sina Moritz als nächstes bei den Chemie-Hausaufgaben helfen wird?
Satz des Pythagoras – Beweis Übung
-
Bestimme die korrekten Aussagen zu einem Beweis zum Satz des Pythagoras.
TippsDer Satz des Pythagoras gilt für alle rechtwinkligen Dreiecke und lautet:
$a^2+b^2=c^2$
Dabei sind $a$ und $b$ Katheten und $c$ ist die Hypotenuse.
Figuren sind kongruent, wenn du sie durch Verschiebung und/oder Drehung ineinander überführen kannst.
LösungDiese Aussagen sind falsch:
„Bei einem rechtwinkligen Dreieck gleicht die Differenz der beiden Kathetenquadrate dem Quadrat der Hypotenuse.“
- Der Satz des Pythagoras gilt für alle rechtwinkligen Dreiecke und lautet: $a^2+b^2=c^2$. Dabei sind $a$ und $b$ die beiden Katheten und $c$ heißt Hypotenuse. Also ist die Summe der beiden Kathetenquadrate gleich dem Quadrat der Hypotenuse.
- Den Flächeninhalt eines Quadrats bestimmst du durch Quadrieren der Seitenlänge. Für die Seitenlänge $a+b$ erhältst du also eine Fläche von $A=(a+b)^2$.
„Den Satz des Pythagoras kannst du mithilfe eines Quadrates beweisen, das aus einem kleineren Quadrat und vier rechtwinkligen Dreiecken zusammengesetzt ist.“
- Anhand der obigen Figur kannst du den Satz des Pythagoras beweisen.
„Zwei kongruente Dreiecke haben jeweils dieselben Winkelgrößen.“
- Figuren sind kongruent, wenn du sie durch Verschiebung und/oder Drehung ineinander überführen kannst. Das geht nur, wenn die beiden Figuren dieselben Winkelgrößen und Seitenlängen besitzen.
-
Beschreibe den Beweis zum Satz des Pythagoras.
TippsGrundsätzlich kannst du eine Fläche immer durch Addition ihrer Teilflächen bestimmen. Hier besteht das große Quadrat aus einem kleineren Quadrat und vier rechtwinkligen Dreiecken.
Bestimmst du den Flächeninhalt einer Fläche auf zwei unterschiedliche Weisen und erhältst zwei unterschiedliche Terme, kannst du diese gleichsetzen. Sie beschreiben nämlich den gleichen Flächeninhalt.
LösungSo kannst du den Lückentext vervollständigen:
„Die Gesamtfläche des großen Quadrats $A_{Q1}$ können wir durch Multiplikation der Seitenlänge $a+b$ bestimmen. So erhalten wir:
$A_{Q1}=(a+b)^2=a^2+2ab+b^2$“
- Hier bestimmen wir die Fläche des großen Quadrats, indem wir die Seitenlängen multiplizieren und den Term anschließend mit der ersten binomischen Formel vereinfachen.
- Grundsätzlich kannst du den Flächeninhalt einer Fläche immer durch Addition ihrer Teilflächen bestimmen. Hier besteht das große Quadrat aus einem kleineren Quadrat und vier rechtwinkligen Dreiecken, deren Fläche wir jetzt berechnen.
$A_D=\frac{1}{2} \cdot a \cdot b$
Der Flächeninhalt des kleinen Quadrats beträgt:
$A_{Q2}=c^2$“
- Hier haben wir die Formeln für die Flächeninhalte der Teilflächen bestimmt. Diese können wir jetzt kombinieren, um die Gesamtfläche anzugeben.
$A_{Q1}=4 \cdot A_D + A_{Q2}=2ab+c^2$“
„Anschließend können wir die beiden Terme des Flächeninhalts $A_{Q1}$ gleichsetzen. So erhalten wir:
$a^2+2ab+b^2=2a b+c^2$"
- Wir haben hier die Fläche des großen Quadrats auf zwei unterschiedliche Weisen bestimmt und zwei unterschiedliche Terme erhalten. Die Terme beschreiben allerdings die gleiche Fläche, also können wir sie gleichsetzen.
$a^2+b^2=c^2$
Das beweist den Satz des Pythagoras.“
- Die Längen $a$ und $b$ sind die Katheten eines rechtwinkligen Dreiecks, während die Länge $c$ seine Hypotenuse ist.
-
Wende den Satz des Pythagoras an.
TippsDu kannst überprüfen, ob die Dreiecke mit den angegebenen Größenangaben rechtwinklig sind, indem du die Katheten $a$ und $b$ in den Satz des Pythagoras einsetzt und überprüfst, ob sich die angegebene Hypotenuse $c$ ergibt.
Der Satz des Pythagoras lautet: Das Hypotenusenquadrat entspricht der Summe der Kathetenquadrate.
LösungDu kannst überprüfen, ob die Dreiecke mit den angegebenen Größenangaben rechtwinklig sind, indem du die Katheten $a$ und $b$ in den Satz des Pythagoras einsetzt und überprüfst, ob sich die angegebene Hypotenuse $c$ ergibt. So erhältst du, dass diese Dreiecke nicht rechtwinklig sind:
„$a=6~\text{cm}$, $b=6~\text{cm}$ und $c=10~\text{cm}$“
- Hier erhältst du: $a^2+b^2= (6~\text{cm})^2 + (6~\text{cm})^2 = 36~\text{cm}^2 + 36~\text{cm}^2= 72~\text{cm}^2$. Das ist ungleich $c^2=(10~\text{cm})^2= 100~\text{cm}^2$. Das Dreieck ist also nicht rechtwinklig.
- Hier erhältst du: $a^2+b^2= (6~\text{cm})^2 + (12~\text{cm})^2 = 36~\text{cm}^2 + 144~\text{cm}^2= 180~\text{cm}^2$. Das ist ungleich $c^2=(13~\text{cm})^2= 169~\text{cm}^2$. Das Dreieck ist also nicht rechtwinklig.
„$a=3~\text{cm}$, $b=4~\text{cm}$ und $c=5~\text{cm}$“
- Hier ergibt sich: $a^2+b^2= (3~\text{cm})^2 + (4~\text{cm})^2 = 25~\text{cm}^2=c^2$
- Hier erhalten wir: $a^2+b^2= (15~\text{cm})^2 + (8~\text{cm})^2 = 17~\text{cm}^2=c^2$
-
Ermittle mithilfe des Satzes des Pythagoras die gesuchten Beziehungen.
TippsFür das große Dreieck kannst du folgende Gleichung aufstellen:
$a^2+b^2=c^2$
Da in dem linken Dreieck der rechte Winkel von den Katheten $h$ und $q$ eingeschlossen wird, erhalten wir:
$h^2+q^2=b^2$
Formst du diese Gleichung nach $h$ um, kannst du eine der Lösungen zuordnen.
LösungDu kannst die Gleichungen zuordnen, indem du die einzelnen Dreiecke betrachtest und den Satz des Pythagoras aufstellst und umformst.
Mit dem großen Dreieck kannst du folgende Formel aufstellen:
$a^2+b^2=c^2$
Stellen wir das nach $b^2$ um, erhalten wir:
- $b^2=c^2-a^2$
- $h^2+p^2=a^2$
- $h^2=a^2-p^2$
- $h=\sqrt{a^2-p^2}$
- $h^2+q^2=b^2$
- $b=\sqrt{h^2+q^2}$
-
Beschreibe die Winkelgrößen der Beweisfigur.
TippsAlle rechten Winkel betragen $90^{\circ}$
Wenn $ \alpha + \beta + 90^{\circ} =180^{\circ}$ gilt, dann folgt daraus:
$ \alpha + \beta = 90^{\circ}$
LösungSo kannst du den Lückentext vervollständigen:
„Hier sind die rechten Winkel des großen Quadrats eingezeichnet. Diese sind gleichzeitig die rechten Winkel der kongruenten Dreiecke. Sie betragen: $90^{\circ}$.“
- Alle rechten Winkel betragen $90^{\circ}$.
- Hier kannst du rechnen: $ \alpha + \beta + 90^{\circ} =180^{\circ} ~\Rightarrow ~ \alpha + \beta = 90^{\circ}$
- Hier kannst du Folgendes rechnen: $ \gamma + 90^{\circ} =180^{\circ} ~\Rightarrow ~ \gamma = 90^{\circ}$
-
Weise den Höhensatz von Euklid nach.
TippsWende den Satz des Pythagoras zuerst auf das große Dreieck und anschließend auf die beiden kleineren Dreiecke an.
In der Gleichung $a^2+b^2=c^2$ kannst du $h^2+p^2$ für $a^2$ und $h^2+q^2$ für $b^2$ einsetzen.
$(p+q)^2$ kannst du mit der ersten binomischen Formel auflösen.
Am Ende musst du zwei Ausdrücke für $c^2$ gleichsetzten und so vereinfachen, dass der Satz des Euklid herauskommt.
LösungSo kannst du den Beweis durchführen:
„Zunächst schreiben wir für die Seitenlängen des großen rechtwinkligen Dreiecks den Satz des Pythagoras auf.
$a^2+b^2=c^2$“
- Hier wenden wir den Satz des Pythagoras auf das große Dreieck an.
$h^2+p^2=a^2$ und
$h^2+q^2=b^2$“
- Hier wenden wir den Satz des Pythagoras auf die beiden kleineren Dreiecke an.
$c^2=a^2+b^2=h^2+p^2+h^2+q^2$“
- Hier setzen wir $h^2+p^2$ für $a^2$ und $h^2+q^2$ für $b^2$ in die Gleichung $c^2=a^2+b^2$ ein.
$c^2=(p+q)^2=p^2 + 2pq +q^2$“
- Hier wurde die erste binomische Formel angewendet.
$c^2=h^2+p^2+h^2+q^2=p^2 + 2pq +q^2$“
- Jetzt können wir alle gefundenen Ausdrücke so zusammenfassen, dass anschließend der Satz des Euklid herauskommt.
$h^2+p^2+h^2=p^2 + 2pq $
Außerdem können wir $p^2$ von beiden Seiten abziehen. Das ergibt:
$h^2+h^2=2pq $
Anschließend fassen wir die $h^2$ Terme zusammen.
$2h^2=2pq $
Teilen wir diese Gleichung durch $2$, erhalten wir den Satz des Euklid:
$h^2=pq $
Was zu beweisen war.“
- Wenn du jetzt denkst, dass du da niemals selbst draufgekommen wärst, dann mach dir keine Sorgen. So geht es jedem, der zum ersten Mal einen Beweis sieht. Beweise sind eine der schwierigsten Aufgaben in der Mathematik. Aber mit der Zeit und mit viel Übung entwickelst du ein Gefühl dafür, wie man sie durchführt.
9.819
sofaheld-Level
6.600
vorgefertigte
Vokabeln
8.306
Lernvideos
38.657
Übungen
33.694
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Klassenstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung


 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?



















Es hat mir sehr geholfen
es ist gut aber man könnte auch ein beispiel mit zahlen machen
Sehr gut erklärt
Ich habs super verstanden. Super erklärt! :-)
Ich verstehe das Thema irgendwie nicht,also das wie man aus einem Quadrat mit diesen Dreiecken also wie man denn Flächen Inhalt berechnet.also die Formel wurde voll komisch erklärt (Also so das ich es nicht verstanden habe)!