Körper – Volumen und Oberfläche
In der Geometrie werden insbesondere Körper behandelt. Körper sind dreidimensionale geometrische Elemente.
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
Was ist ein Körper?
- Ein Körper ist dreidimensional. Einen Körper kannst du also umfassen.
- Ein Körper wird begrenzt durch Flächen. Diese sind zweidimensional. Dabei können die begrenzenden Flächen eben (zum Beispiel bei einem Würfel) oder gekrümmt (zum Beispiel bei einer Kugel) sein.
- Ein Körper kann Ecken und Kanten haben.
Hier kannst du verschiedene geometrische Grundkörper identifizieren:
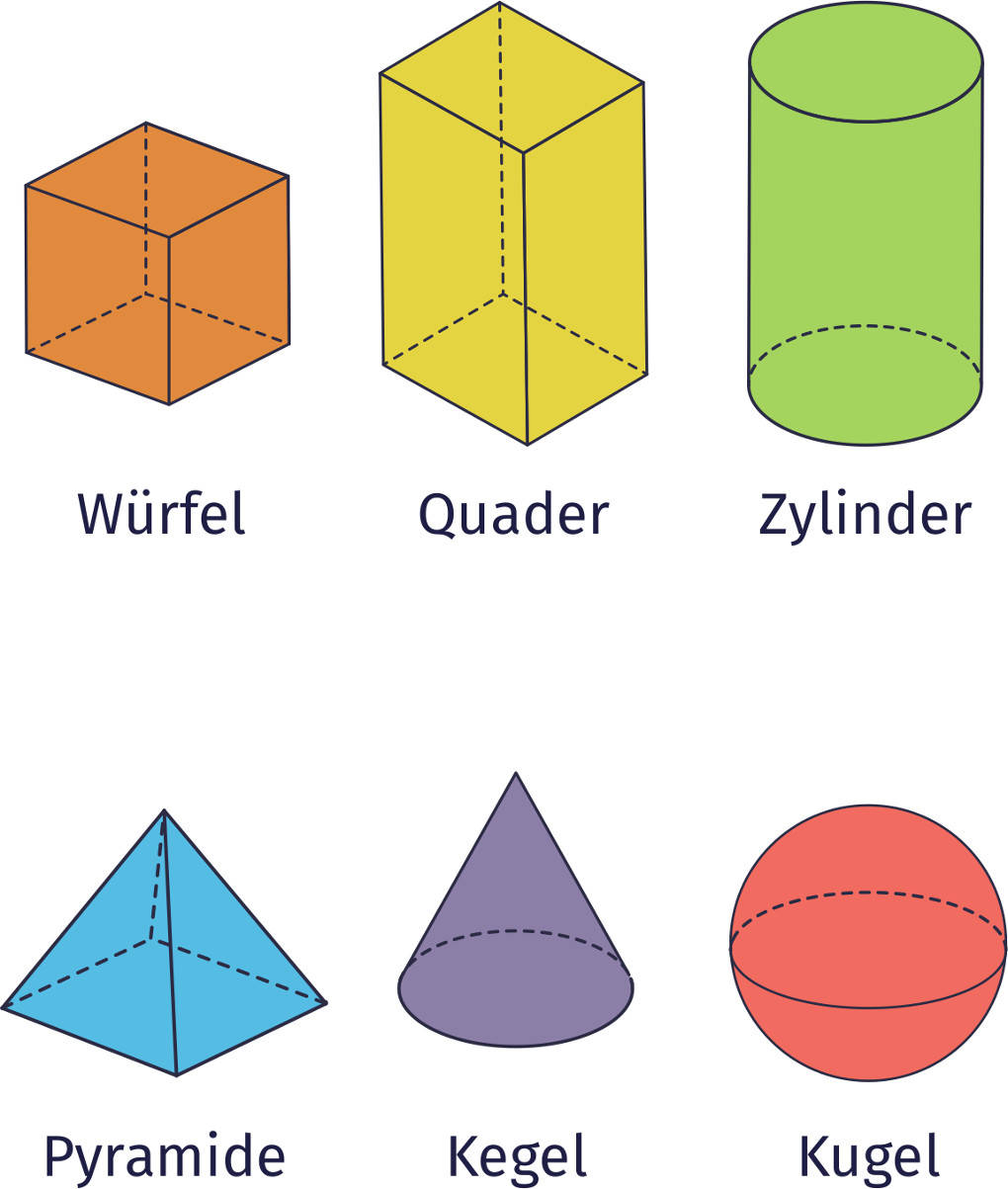
Im Folgenden lernst du zu den verschiedenen Körpern, wie viele Flächen den jeweiligen Körper begrenzen sowie die entsprechende Anzahl an Ecken und Kanten.
Würfel, Quader und Prisma
Würfel, Quader und Prisma sind jeweils Körper mit kongruenten und zueinander parallelen Vielecken als Grund- und Deckfläche. Die einander entsprechenden Ecken dieser Vielecken werden mit Höhen verbunden, welche senkrecht sowohl zu der Grund- als auch der Deckfläche stehen.
Würfel und Quader
Bei einem Würfel sind alle Grenzflächen Quadrate, bei einem Quader Rechtecke. Ansonsten sind diese beiden Körper recht ähnlich. Beide haben
- $6$ Grenzflächen,
- $8$ Ecken und
- $12$ Kanten.
Die Anzahl der Flächen kannst du dir zum Beispiel mit Hilfe eines Spielwürfels klarmachen. Bei diesem befinden sich auf den Flächen die Augenzahlen von $1$ bis $6$:

Prisma
Ein Prisma setzt sich immer aus zwei beliebigen, aber deckungsgleichen (kongruenten) Vielecken als Grund- und Deckfläche zusammen. Sie sind über Kanten an den Vielecken miteinander verbunden. Ganz allgemein gilt für ein Prisma mit einem $n$-Eck als Grundfläche:
- Die Anzahl der Flächen beträgt $n+2$,
- die der Ecken $2n$ und
- die der Kanten $3n$.
Hier siehst du ein Beispiel für ein Prisma, aber es gibt noch sehr viele andere, die sehr unterschiedlich aussehen können:
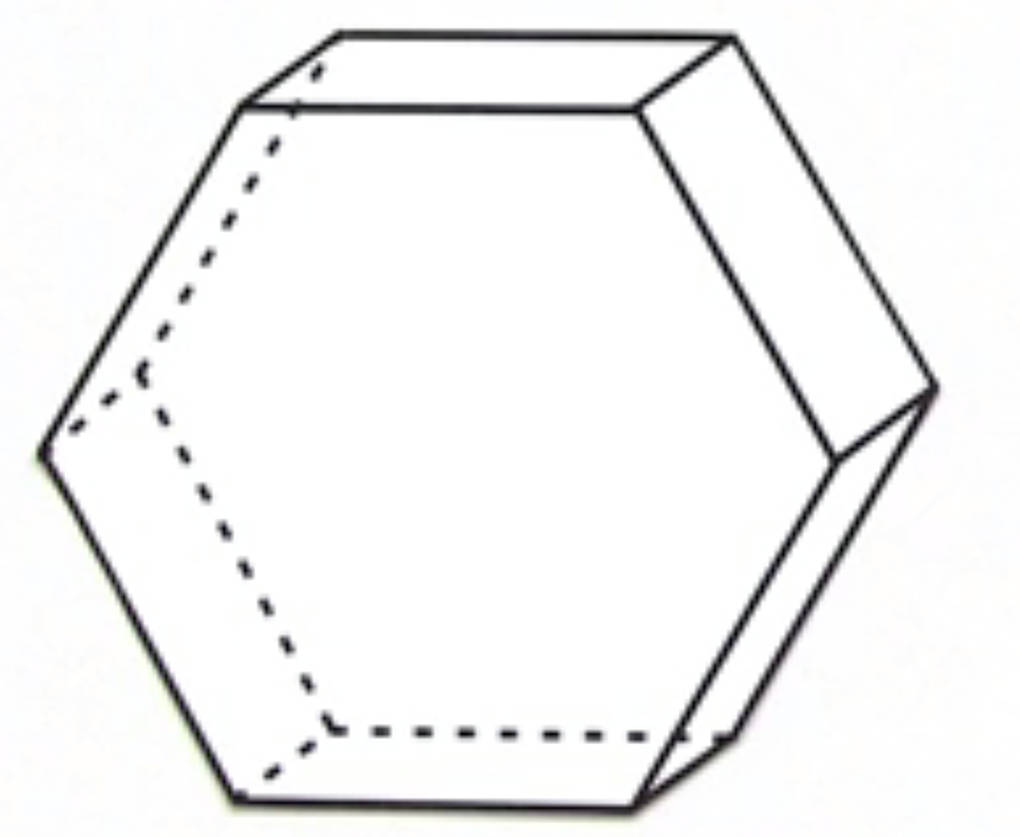
Zylinder, Pyramide, Kegel und Kugel
Schließlich schauen wir uns noch die Eigenschaften von Zylinder, Pyramide, Kegel und Kugel an. Zylinder, Kegel und Kugel zeichnen sich dadurch aus, dass sie auch, oder ausschließlich, gekrümmte Flächen besitzen. Pyramiden haben dagegen nur ebene Flächen.
Pyramide
Vielleicht hast du schon einmal etwas über die Pyramiden in Ägypten gesehen oder gelesen. Diese sehen so aus:
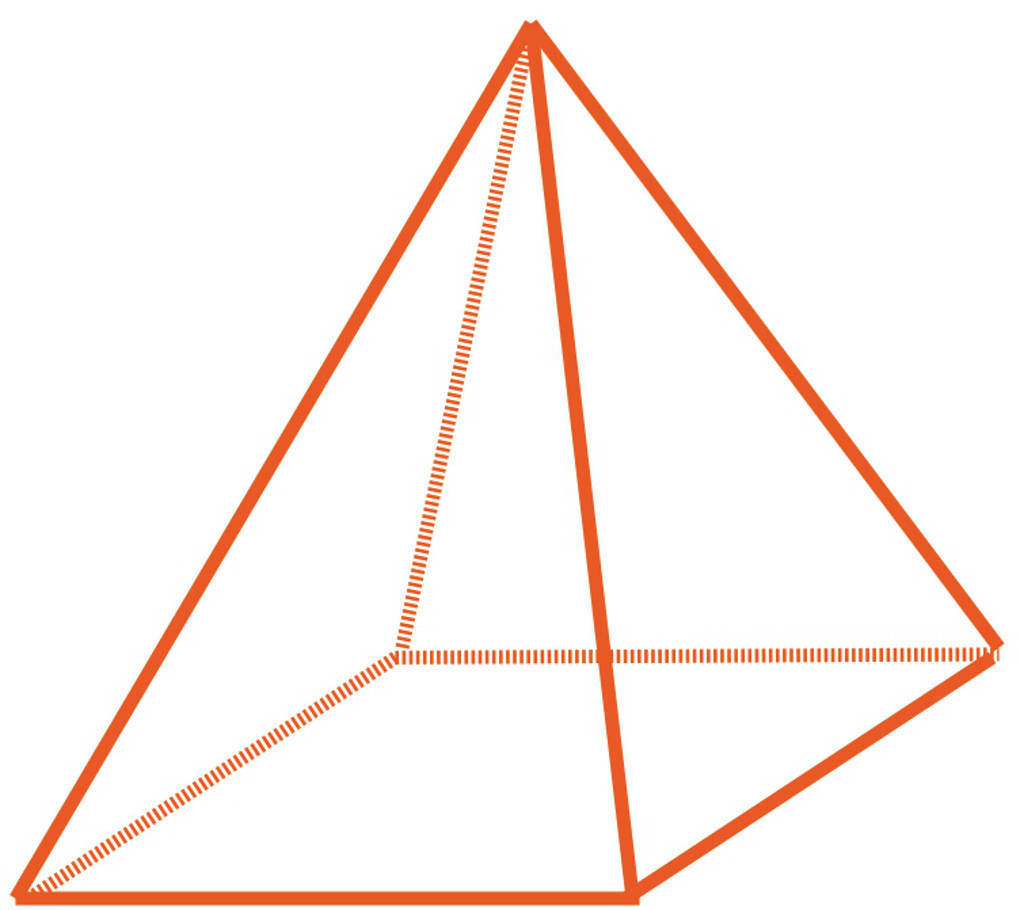
Hier siehst du eine gerade Pyramide mit quadratischer Grundfläche: Jeder Eckpunkt der Grundfläche wird mit der Spitze der Pyramide verbunden. Diese Pyramide hat $5$ begrenzende Flächen, $5$ Ecken und $8$ Kanten.
Zylinder
So sieht ein Zylinder aus:

Ein Zylinder hat als Grund- und Deckfläche zueinander kongruente Kreise. Der Abstand der beiden Kreise zueinander ist die Höhe des Zylinders. Ein Glas hat oft die Form eines Zylinders. Allerdings hat ein Glas keine Deckfläche, sonst könntest du ja nichts in dieses Glas füllen.
Ein Zylinder hat $3$ begrenzende Flächen, keine Ecke und $2$ Kanten.
Kegel
Eine Eistüte hat die Form eines Kegels. Hier siehst du einen Kegel:
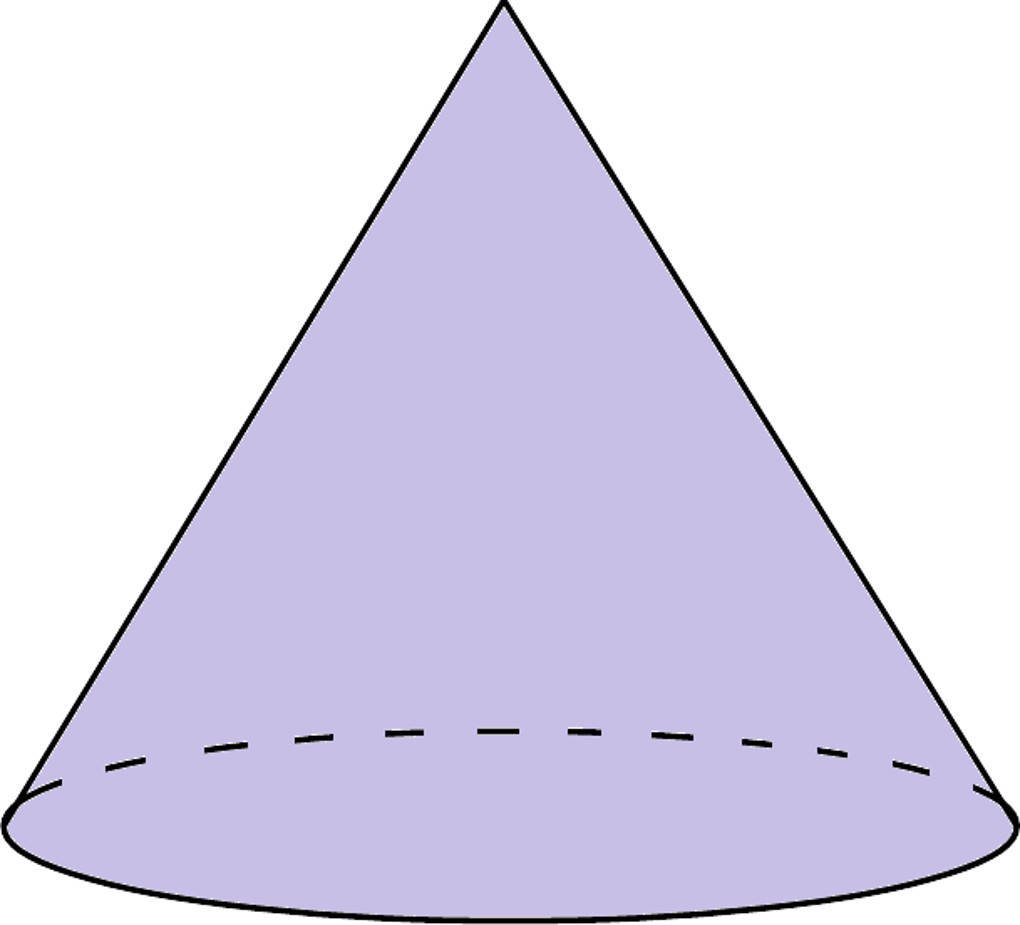
Ein Kegel hat einen Kreis als Grundfläche. Jeder Randpunkt des Kreises wird mit der Spitze des Kegel verbunden. Das ist so ähnlich wie bei der Pyramide. Ein Kegel hat $2$ begrenzende Flächen, eine Ecke und eine Kante.
Kugel
Die Weltkugel ist, das erkennst du bereits am Namen, eine Kugel.
Eine Kugel unterscheidet sich doch sehr von den bisherigen Körpern. Wie der Kegel hat die Kugel eine gekrümmte Begrenzungsfläche. Eine Kugel hat allerdings weder eine Ecke noch eine Kante.
Alle Videos und Lerntexte zum Thema
Videos und Lerntexte zum Thema
Körper – Volumen und Oberfläche (8 Videos, 1 Lerntext)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Körper – Volumen und Oberfläche (9 Arbeitsblätter)
-
 Geometrische Grundkörper identifizieren
PDF anzeigen
Geometrische Grundkörper identifizieren
PDF anzeigen -
 Würfel – Volumen und Oberfläche
PDF anzeigen
Würfel – Volumen und Oberfläche
PDF anzeigen -
 Quader – Volumen und Oberfläche
PDF anzeigen
Quader – Volumen und Oberfläche
PDF anzeigen -
 Volumen von Körpern – Grundfläche und Höhe
PDF anzeigen
Volumen von Körpern – Grundfläche und Höhe
PDF anzeigen -
 Oberflächeninhalt eines Prismas berechnen
PDF anzeigen
Oberflächeninhalt eines Prismas berechnen
PDF anzeigen -
 Volumen von Prismen berechnen
PDF anzeigen
Volumen von Prismen berechnen
PDF anzeigen -
 Volumen von zusammengesetzten Würfeln und Quadern
PDF anzeigen
Volumen von zusammengesetzten Würfeln und Quadern
PDF anzeigen -
 Quader – Begriffe und Eigenschaften
PDF anzeigen
Quader – Begriffe und Eigenschaften
PDF anzeigen -
 Kantenlänge eines Quaders bestimmen
PDF anzeigen
Kantenlänge eines Quaders bestimmen
PDF anzeigen
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung




















