Quadratische Funktionen

Inhaltsverzeichnis zum Thema

• Einführung quadratische Funktion und Nullstellen
  • Was ist eine quadratische Funktion?
  • Was ist eine Nullstelle?
• Nullstellen von quadratischen Funktionen
• Wie viele Nullstellen kann eine quadratische Funktion besitzen?
  • Zwei Nullstellen
  • Eine Nullstelle
  • Keine Nullstelle

Einführung quadratische Funktion und Nullstellen

Was ist eine quadratische Funktion?

Eine quadratische Funktion $f$ kann in der Form $f(x)=ax^2+bx+c$ vorliegen.

Diese Allgemeinform quadratischer Funktionen enthält die Parameter $a$, $b$ und $c$. Außerdem werden dir auch quadratische Funktionen in der Scheitelpunktform begegnen. In diesem Text werden wir die Allgemeinform weiter betrachten. Der Funktionsgraph einer quadratischen Funktion wird als Parabel bezeichnet.

Weißt du noch, wie eine Parabel aussieht? Betrachte die quadratische Funktion $f$ mit $f(x)=x^2+4x+3$. Den zugehörigen Funktionsgraphen kannst du hier sehen.

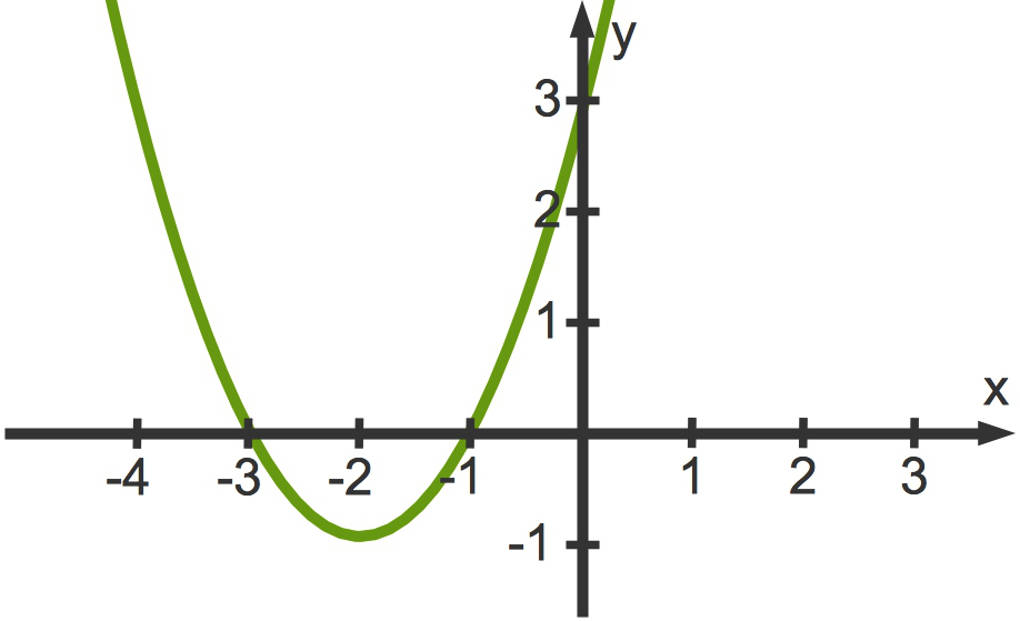
Dies ist eine nach oben geöffnete Parabel. Diese Parabel schneidet die $x$-Achse bei den $x$-Werten $-3$ und einmal bei $-1$.

Die Schnittstellen eines Funktionsgraphen mit der $x$-Achse werden Nullstellen genannt.

Was ist eine Nullstelle?

Eine Nullstelle ist ein Wert für $x$, welcher eingesetzt in die Funktionsgleichung von $f$ den Wert $0$ ergibt. Wie viele Nullstellen es gibt, hängt von der jeweiligen Funktion ab.

Nullstellen findest du nicht immer durch Probieren oder Ablesen. Du musst die Gleichung $f(x)=0$ lösen.

Als Beispiel ist die lineare Funktion $f$ mit $f(x)=x-4$ gegeben. Deren Funktionsgraph, eine Gerade, siehst du hier:

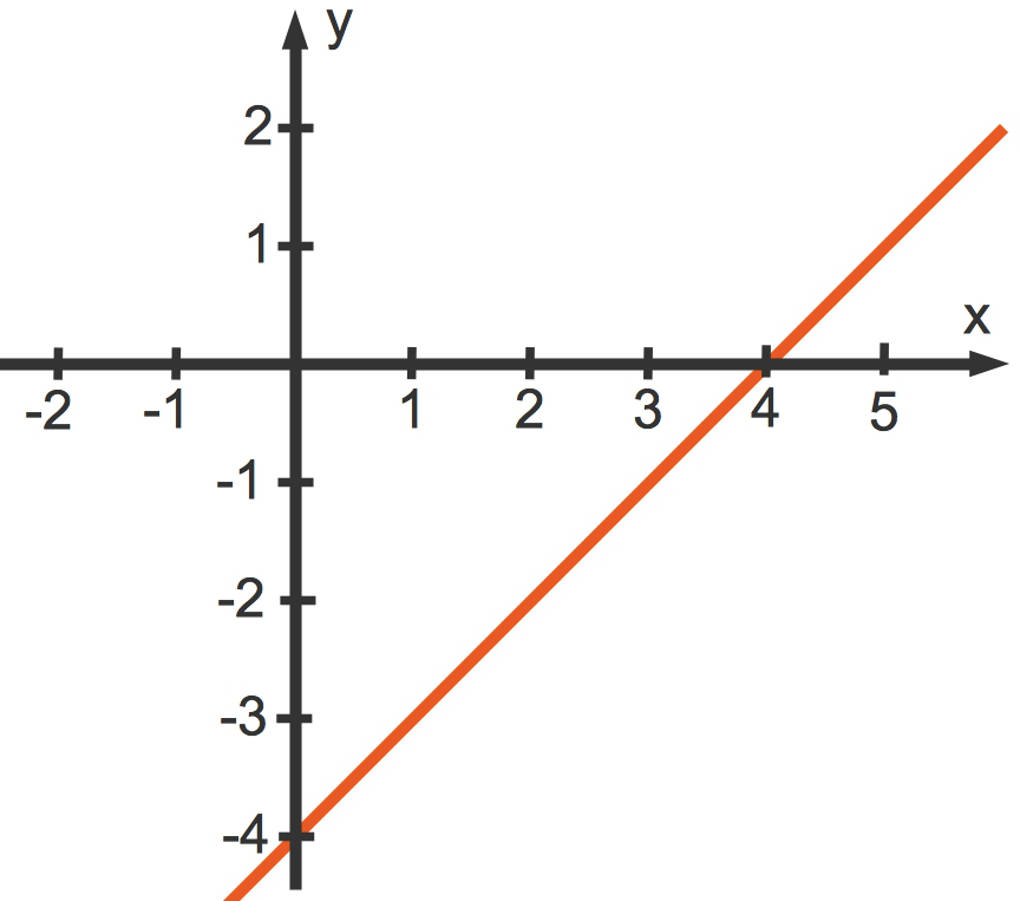
Zur Bestimmung der Nullstelle, löst du die Gleichung $x-4=0$. Addiere $4$, so erhältst du $x=4$, die Nullstelle, die du auch an dem Funktionsgraphen sehen kannst.

In Klausuren wird häufig nach den Schnittstellen mit den Koordinatenachsen gefragt:

• Die Schnittstellen mit der $x$-Achse sind die Nullstellen.
• Es kann auch maximal eine Schnittstelle mit der $y$-Achse geben. Diese erhältst du durch Einsetzen von $x=0$ in die Funktionsgleichung.

Nullstellen von quadratischen Funktionen

Auch bei quadratischen Funktionen löst du die Gleichung $f(x)=0$. Dies führt zu der quadratischen Gleichung $ax^2+bx+c=0$. Weißt du noch, wie du eine quadratische Gleichung löst? Du verwendest die p-q-Formel. Der quadratische Term links vom Gleichheitszeichen muss hierfür in Normalform sein. Das bedeutet, vor dem $x^2$ steht der Faktor $1$. Andernfalls dividierst du durch den Faktor vor dem $x^2$. Hier siehst du die p-q-Formel zur Lösung der quadratischen Gleichung in Normalform $x^2+px+q=0$:

$x_{1,2}=-\frac p2\pm\sqrt{\left(\frac p2\right)^2-q}$.

Nun kannst du die Nullstellen der quadratischen Funktion $f$ mit $f(x)=x^2+4x+3$ berechnen. Hier ist $p=4$ und $q=3$:

$\begin{array}{rcl} x_{1,2}&=&-\frac 42\pm\sqrt{\left(\frac 42\right)^2-3}\\ &=&-2\pm\sqrt{4-3}\\ x_1&=&-2+1=-1\\ x_2&=&-2-1=-3 \end{array}$

Dies sind die Nullstellen, die du bereits an dem erkennen konntest.

Wie viele Nullstellen kann eine quadratische Funktion besitzen?

Eine quadratische Funktion kann maximal zwei Nullstellen besitzen. Der Term unter der Wurzel in der p-q-Formel gibt dir einen Hinweis darauf, wie viele Nullstellen die Funktion hat.

Zwei Nullstellen

Bei dem obigen Beispiel hast du bereits gesehen, dass eine quadratische Funktion zwei Nullstellen besitzen kann. Der Term unter der Wurzel in der p-q-Formel ist in dem Beispiel mit $3$ positiv.

Übrigens: Wenn der Funktionsgraph zwei Nullstellen besitzt, dann liegt genau in der Mitte dieser beiden Nullstellen die $x$-Koordinate des Scheitelpunktes. Das ist kein Zufall. Parabeln sind achsensymmetrisch. Die Symmetrieachse verläuft parallel zu der $y$-Achse durch den Scheitelpunkt. Das bedeutet, dass für den Fall zweier Nullstellen diese den gleichen Abstand zu der $x$-Koordinate des Scheitelpunktes haben müssen.

Eine Nullstelle

Der Funktionsgraph der Funktion $g(x)=x^2+4x+4$ entsteht aus dem obigen Funktionsgraphen zu $f(x)=x^2+4x+3$ durch Verschiebung um eine Längeneinheit nach oben, also entlang der $y$-Achse.

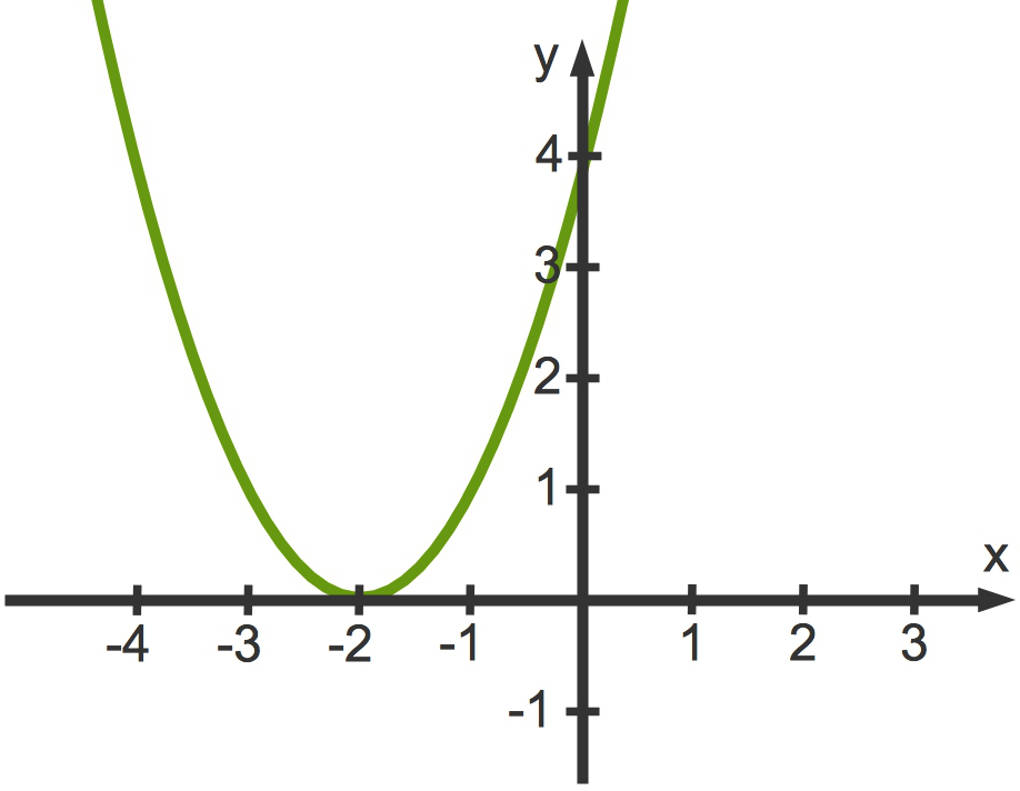
Die Gleichung $x^2+4x+4=0$ führt zu:

$\begin{array}{rcl} x_{1,2}&=&-\frac 42\pm\sqrt{\left(\frac 42\right)^2-4}\\ &=&-2\pm\sqrt{4-4}\\ x_1&=&-2\pm 0=-2 \end{array}$

Der Term unter der Wurzel, dieser wird übrigens Diskriminante genannt, ist $0$. Es gibt nur eine Nullstelle. Der Funktionsgraph berührt die $x$-Achse. Der Berührpunkt ist der Scheitelpunkt der Parabel.

Keine Nullstelle

Der Funktionsgraph der Funktion $h(x)=x^2+4x+5$ entsteht aus dem obigen Funktionsgraphen zu $f(x)=x^2+4x+3$ durch Verschiebung um zwei Längeneinheiten nach oben.

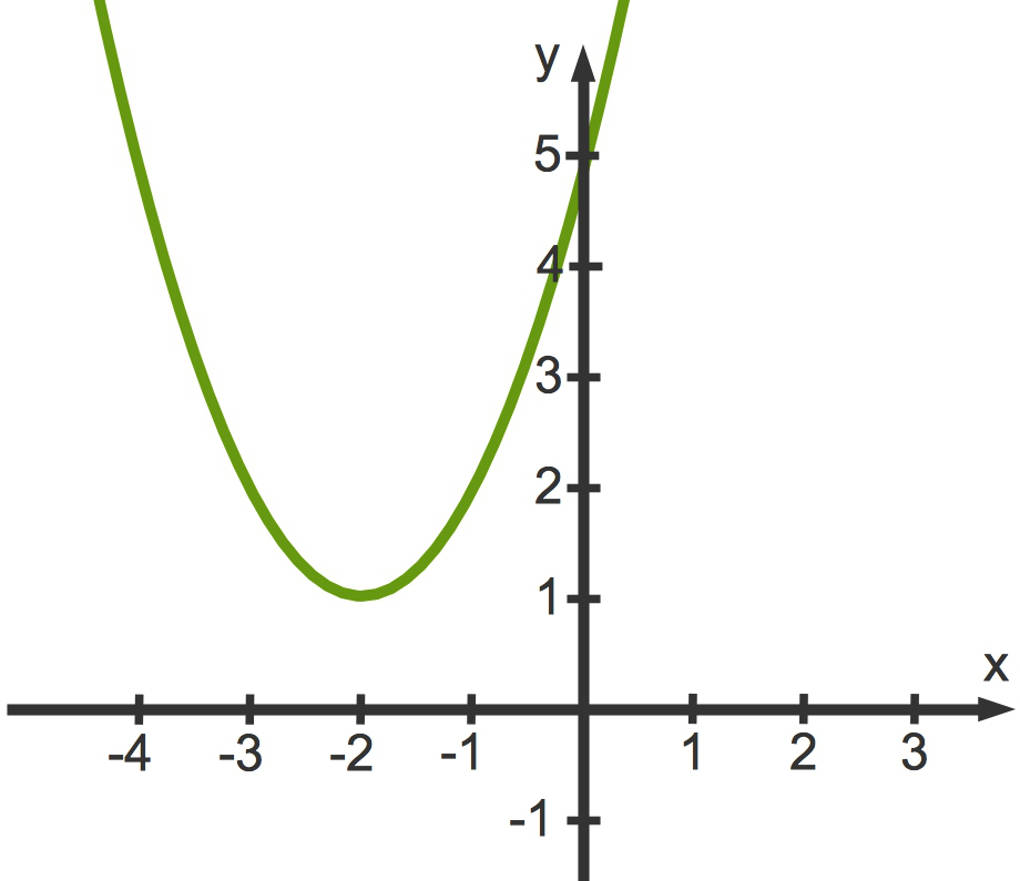
Die Gleichung $x^2+4x+5=0$ führt zu

$\begin{array}{rcl} x_{1,2}&=&-\frac 42\pm\sqrt{\left(\frac 42\right)^2-5}\\ &=&-2\pm\sqrt{4-5}\\ &=&-2\pm \sqrt{-1} \end{array}$

Der Term unter der Wurzel ist in diesem Beispiel negativ. Da du die Wurzel aus einer negativen Zahl nicht ziehen kannst, gibt es keine Lösung der Gleichung. Der Funktionsgraph hat also keine Nullstelle.