Zweiter Strahlensatz – Einführung

Zweiter Strahlensatz – Einführung Übung

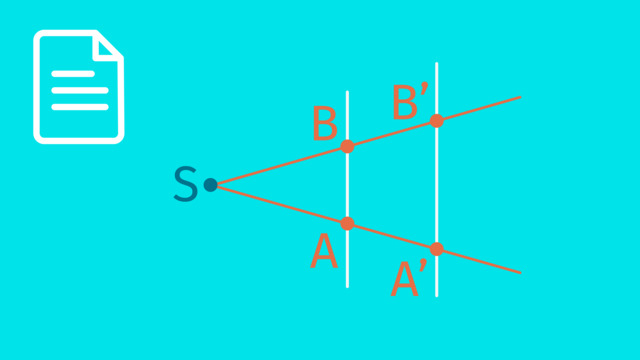
• Beschrifte die Strahlensatzfigur.

  Tipps

  Eine Streckenbezeichnung besteht immer aus dem Anfangs- und Endpunkt. Darüber zeichnest du einen Strich. Zum Beispiel verläuft die Strecke $ \overline{A_1 B_1}$ zwischen den Punkten $A_1$ und $B_1$.

  Parallelen haben überall den gleichen Abstand zueinander.

  Lösung

  So kannst du die Strahlensatzfigur vervollständigen:

  • Eine Streckenbezeichnung besteht immer aus dem Anfangs- und Endpunkt. Darüber zeichnest du einen Strich. Zum Beispiel: $ \overline{ZB_2}$

  • Die Bezeichnung der Punkte kannst du genauso aus den Streckenbezeichnungen erkennen. $\overline{ZB_2}$ verläuft zwischen den Punkten $Z$ und $B_2$

  • Strahlen sind die Geraden, die aus dem gemeinsamen Punkt $Z$ entspringen. Parallelen haben überall den gleichen Abstand zueinander.

• Berechne die fehlende Länge mit dem zweiten Strahlensatz.

  Tipps

  So könnte eine Skizze zu der Situation aussehen.

  Die Verhältnisgleichung besteht aus zwei Verhältnissen. Eine Merkregel kann lauten, dass du jeweils die beiden längeren und die beiden kürzeren Strecken zuerst ins Verhältnis und anschließend gleichsetzt. Dabei musst du darauf achten, dass du in beiden Verhältnissen die gleichen Strecken (z.B. die Strecken auf den Strahlen) durch die anderen teilst (z.B. die Strecken auf den Parallelen).

  Lösung

  Die Rechnung kannst du so vervollständigen:

  Zuerst stellen die beiden eine Verhältnisgleichung auf. Dazu teilen sie die längere Strecke des Strahls $\overline{ZB_2}$ durch die längere Strecke der Parallelen $\overline{A_2B_2}$. (...)

  Das andere Verhältnis besteht aus der kürzeren Strecke des Strahls $\overline{ZB_1}$, geteilt durch die kürzere Strecke der Parallelen $\overline{A_1B_1}$. (...)

  • Die Verhältnisgleichung besteht aus zwei Verhältnissen. Eine Merkregel kann lauten, dass du jeweils die beiden längeren und die beiden kürzeren Strecken zuerst ins Verhältnis und anschließend gleichsetzt. Dabei musst du darauf achten, dass du in beiden Verhältnissen die gleichen Strecken (z. B. die Strecken auf den Strahlen) durch die anderen teilst (z. B. die Strecken auf den Parallelen).

  Durch Gleichsetzen erhalten sie folgende Verhältnisgleichung:

  $\dfrac{\overline{ZB_2}}{\overline{A_2B_2}}=\dfrac{\overline{ZB_1}}{\overline{A_1B_1}}$

  • Wie du hier siehst, wurde auf der linken Seite der Gleichung die längere Strecke auf dem Strahl durch die längere Parallele geteilt. Auf der rechten Seite steht entsprechend die kürzere Strecke auf dem Strahl geteilt durch die kürzere Parallele.

  Hier können sie die gegebenen Längen einsetzen:

  $\frac{\overline{ZB_2}}{9}=\frac{6}{3}$

  Durch Umformen erhalten sie:

  $\overline{ZB_2}=\frac{6}{3} \cdot 9= 18$

  Kunigunde muss also $18$ Längeneinheiten von der Kamera entfernt stehen.

  • Hast du die Gleichung aufgestellt, musst du noch die gegebenen Zahlen einsetzen und nach der gesuchten Größe umstellen.

• Bestimme die korrekten Aussagen zu dieser Strahlensatzfigur.

  Tipps

  Eine Verhältnisgleichung nach dem zweiten Strahlensatz kann lauten:

  $\dfrac{\overline{A_2B_2}}{\overline{A_1B_1}}=\dfrac{\overline{ZB_2}}{\overline{ZB_1}}$

  Diese Gleichung kannst du durch Äquivalenzumformungen umstellen.

  Der zweite Strahlensatz trifft eine Aussage zu den Streckenverhältnissen von den zwei Strecken auf einem Strahl zu den zwei Strecken auf den beiden Parallelen.

  Lösung

  Folgende Aussagen sind falsch:

  „Nach dem zweiten Strahlensatz könnte eine Verhältnisgleichung so aussehen:

  $\dfrac{\overline{ZB_1}}{\overline{ZB_2}}=\dfrac{\overline{ZA_1}}{\overline{ZA_2}}$“

  • Dies ist zwar eine korrekte Strahlensatzgleichung, allerdings wurde hier der erste Strahlensatz angewandt. Das kannst du erkennen, da hier keine der Parallelen in der Gleichung vorkommt.

  „Dies ist ebenfalls eine korrekte Verhältnisgleichung nach dem zweiten Strahlensatz:

  $\dfrac{\overline{A_2B_2}}{\overline{ZB_1}}=\dfrac{\overline{A_1B_1}}{\overline{ZA_1}}$“

  • Eine Verhältnisgleichung kannst du beispielsweise aufstellen, indem du jeweils die beiden längeren und die beiden kürzeren Strecken zuerst ins Verhältnis und anschließend gleichsetzt. Dabei musst du darauf achten, dass du in beiden Verhältnissen die gleichen Strecken (z.B. die Strecken auf den Parallelen) durch die anderen teilst (z.B. die Strecken auf den Strahlen). Dann ergibt sich beispielsweise: $\dfrac{\overline{A_2B_2}}{\overline{ZB_2}}=\dfrac{\overline{A_1B_1}}{\overline{ZB_1}}$ Diese Gleichung kannst du durch Äquivalenzumformungen umstellen.

  „Sind die Längen $\overline{ZB_1}=3$, $\overline{ZB_2}=4$ und $\overline{A_1B_1}=8$ gegeben, ergibt sich für $\overline{A_2B_2}=6$“

  • Hier ergibt sich für $\overline{A_2B_2}= \frac{\overline{A_1B_1}}{\overline{ZB_1}} \cdot \overline{ZB_2} =\frac{8}{3} \cdot 4=\frac{32}{3}$

  Diese Aussagen sind korrekt:

  „Sind die Längen $\overline{ZB_2}=4$, $\overline{ZB_2}=3$ und $\overline{A_1B_1}=8$ gegeben, ergibt sich für $\overline{A_2B_2}=6$“

  „Eine korrekte Verhältnisgleichung nach dem zweiten Strahlensatz könnte so aussehen:

  $\dfrac{\overline{A_2B_2}}{\overline{ZB_2}}=\dfrac{\overline{A_1B_1}}{\overline{ZB_1}}$“

• Ermittle die fehlenden Längen mit dem zweiten Strahlensatz.

  Tipps

  So kann eine Strahlensatzfigur aussehen.

  Eine Strahlensatzfigur kannst du mit beiden Strahlen aufstellen. Du kannst also

  $\dfrac{\overline{A_2B_2}}{\overline{ZA_2}}=\dfrac{\overline{A_1B_1}}{\overline{ZA_1}}$

  mit dem Strahl, auf dem die Punkte $A_1$ und $A_2$ liegen, aufstellen. Genauso kannst du das mit dem Strahl, auf dem die Punkte $B_1$ und $B_2$ liegen, tun.

  Lösung

  Um die fehlenden Längen zu berechnen, musst du die richtigen Strahlensätze aufstellen, die gegebenen Längen in die Gleichung einsetzen und umformen. Für die erste Lücke stellst du diesen Strahlensatz auf:

  $\dfrac{\overline{A_2B_2}}{\overline{ZB_2}}=\dfrac{\overline{A_1B_1}}{\overline{ZB_1}}$

  Anschließend setzt du die gegebenen Werte ein:

  $\dfrac{\overline{A_2B_2}}{10}=\dfrac{1}{5}$

  Zuletzt stellst du um und rechnest aus:

  • $\overline{A_2B_2}= \dfrac{1}{5} \cdot 10= 2$

  Für die zweite Länge ergibt sich:

  $\dfrac{\overline{A_2B_2}}{\overline{ZA_2}}=\dfrac{\overline{A_1B_1}}{\overline{ZA_1}} ~\Leftrightarrow ~ \dfrac{\overline{ZA_2}}{\overline{A_2 B_2}}=\dfrac{\overline{ZA_1}}{\overline{A_1 B_1}}$

  Einsetzen und Ausrechnen ergibt:

  • $\overline{ZA_2}= \dfrac{3}{9} \cdot 3= 1$

  • Für die dritte Figur ergibt sich ähnlich: $\overline{A_1B_1}=12$.

  • Und schließlich: $\overline{ZA_1}=20$

• Bestimme die korrekten Aussagen zum zweiten Strahlensatz.

  Tipps

  So kann eine Strahlensatzfigur aussehen.

  Bei obigem Bild kannst du mit dem zweiten Strahlensatz folgende Verhältnisgleichung aufstellen:

  $\dfrac{\overline{ZB_2}}{\overline{A_2B_2}}=\dfrac{\overline{ZB_1}}{\overline{A_1B_1}}$

  Lösung

  Diese Aussagen sind falsch:

  „Kennst du zwei Längen der Strahlensatzfigur, kannst du die letzte Strecke ausrechnen.“

  • Um Strahlensätze anzuwenden, brauchst du immer insgesamt vier Strecken, von denen eine unbekannt ist.

  „In einer Strahlensatzfigur entspricht die Differenz der beiden längeren Strecken genau der Differenz der beiden kürzeren Strecken.“

  • Mit den Strahlensätzen kannst du Verhältnisgleichungen aufstellen. Das sind Gleichungen, die aus zwei Quotienten (das Ergebnis einer Division) bestehen. Eine Differenz ist das Ergebnis einer Subtraktion.

  Diese Aussagen sind richtig:

  „Schneiden zwei Parallelen zwei Strahlen, die von einem gemeinsamen Punkt ausgehen, kannst du den zweiten Strahlensatz anwenden.“

  „Die Strahlensätze sind auch anwendbar, wenn sich zwei Geraden schneiden und die Parallelen auf unterschiedlichen Seiten des Schnittpunkts liegen.“

  • So können Strahlensatzfiguren aussehen.

  „Um eine Verhältnisgleichung aufzustellen, teilst du jeweils zwei Längen durch einander und setzt sie gleich. Du musst jedoch immer die zwei längeren durch die beiden kürzeren Strecken, oder die zwei kürzeren durch die beiden längeren Strecken teilen.“

  Die folgende Kombination ist nicht möglich: $\dfrac{\text{lang}}{\text{kurz}}=\dfrac{\text{kurz}}{\text{lang}}$

• Arbeite die korrekten Aussagen heraus.

  Tipps

  So kann eine Strahlensatzfigur aussehen, in der die Parallelen auf unterschiedlichen Seiten des Schnittpunkts $Z$ zweier Geraden liegen.

  Lösung

  Diese Aussage ist falsch:

  „Mit dem ersten Strahlensatz kannst du nur Strecken auf den Strahlen berechnen, während du mit dem zweiten Strahlensatz nur Strecken auf den Parallelen berechnen kannst.“

  • Mit dem ersten Strahlensatz kannst du in der Tat nur Strecken auf den Strahlen berechnen, allerdings kannst du den zweiten Strahlensatz verwenden, um sowohl Strecken auf den Parallelen als auch Strecken auf den Strahlen zu berechnen.

  Diese Aussagen sind richtig:

  „In einer Figur, in der du mit dem ersten Strahlensatz Strecken auf den Strahlen berechnen kannst, kannst du auch den zweiten Strahlensatz verwenden, um Strecken auf den Parallelen zu bestimmen.“

  „Eine Verhältnisgleichung, die mit dem ersten Strahlensatz aufgestellt wurde, kann heißen:

  $\dfrac{\overline{ZB_2}}{\overline{ZB_1}}=\dfrac{\overline{ZA_2}}{\overline{ZA_1}}$.“

  • Beim ersten Strahlensatz verwendest du dieselbe Strahlensatzfigur, allerdings stellst du nur Strecken auf den Strahlen ins Verhältnis. Eine Faustregel kann lauten: Teile die kürzere Strecke auf einem Strahl durch die längere Strecke auf dem gleichen Strahl. Teile dann die kürzere Strecke auf dem anderen Strahl durch die längere Strecke auf dem gleichen Strahl. Setze anschließend die Verhältnisse gleich.

  „Eine Strahlensatzfigur, in der die Parallelen auf unterschiedlichen Seiten des Schnittpunkts $Z$ zweier Geraden liegen, kannst du durch eine Punktspiegelung an $Z$ auf eine Strahlensatzfigur zurückführen, in der zwei Strahlen einem gemeinsamen Punkt $Z$entspringen und die Parallelen auf der gleichen Seite dieses Punktes liegen.“

  • Du kannst tatsächlich mit einer Punktspiegelung die beiden Strahlensatzfiguren ineinander überführen. Dabei bleiben die Längen der Figur nämlich erhalten.

  „In einer Strahlensatzfigur bezeichnet man üblicherweise Punkte auf einer Geraden mit dem gleichen Buchstaben, aber nummeriert diese. Wenn du möchtest, kannst du diese Bezeichnungen aber auch frei wählen.“

  • Nur wenn du diese Konvention beibehältst, haben die Verhältnisgleichungen der Strahlensätze Sinn. Änderst du die Bezeichnungen, musst du auch die Variablen in den Verhältnisgleichungen ändern.