Strahlensätze – Entfernungen im Gelände
- Strahlensätze – Entfernungen mit dem Daumensprung abschätzen
- Der Daumensprung in sechs Schritten
- Kürzere Variante des Daumensprungs
- Welche Fehlerquellen gibt es beim Daumensprung?
in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.

Lerntext zum Thema Strahlensätze – Entfernungen im Gelände
Strahlensätze – Entfernungen mit dem Daumensprung abschätzen
Die Strahlensätze wirken im Unterricht sehr abstrakt und theoretisch. Wie sie aber eine sehr pragmatische Anwendung im Alltag finden können, zeigt der Daumensprung. Dieser ist besonders bei Naturliebhabenden beliebt, die öfter mal im Freien unterwegs sind.
Der Daumensprung ist eine Methode, um Entfernungen abzuschätzen. Du brauchst dafür kein Maßband oder Ähnliches, sondern nur deinen eigenen Körper. Die Methode funktioniert in der Natur, aber auch bei größeren Abständen in einem Gebäude.
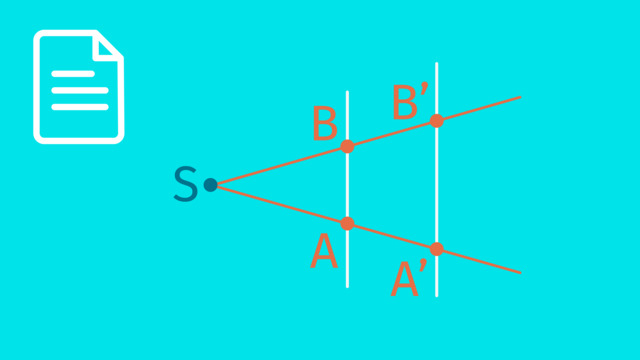
Zur Wiederholung noch einmal die Strahlensätze in Kurzform:
$\text{Erster Strahlensatz: } \dfrac{\overline{SA'}}{\overline{SA}} = \dfrac{\overline{SB'}}{\overline{SB}} \newline {}\newline$
In Worten: „Große Strecke durch kleine Strecke gleich große Strecke durch kleine Strecke.“
Der Daumensprung in sechs Schritten
Für den Daumensprung musst du zwei Messwerte kennen:
- deinen Augenabstand, der durchschnittlich ungefähr $\pu{6 cm}$ beträgt und
- deine Armlänge, die bei Fünfzehnjährigen durchschnittlich $\pu{50 cm}$ beträgt.
Wenn du beim Daumensprung noch genauer sein möchtest, kannst du auch deinen eigenen Augenabstand und deine Armlänge von der Schulter bis zum Daumenansatz messen.
Schritt 1: Arm ausstrecken und Daumen aufstellen
Im ersten Schritt streckst du einen Arm in die Richtung, in die du eine Entfernung abschätzen möchtest, und stellst den Daumen auf.
Schritt 2: ein Auge schließen und Ziel anpeilen
Im zweiten Schritt schließt du eines deiner beiden Augen und peilst mit dem anderen Auge dein Ziel an.
Schritt 3: Auge öffnen
Im dritten Schritt öffnest du das Auge wieder und schließt dein anderes Auge. Dein Daumen ist nun scheinbar zur Seite „gesprungen“.
Schritt 4: Daumensprung schätzen
Im vierten Schritt schätzt du, wie weit dein Daumen in etwa gesprungen ist. Dabei kannst du dich an z. B. Bäumen, Häusern oder Gegenständen orientieren, deren Breite du kennst oder gut abschätzen kannst.
Schritt 5: Werte einsetzen
Im fünften Schritt kannst du nun die geschätzte Entfernung berechnen. Dafür nutzt du den ersten Strahlensatz und setzt die Werte in diese Gleichung ein:
$\text{Armlänge} : \text{Augenabstand} = y : x$
Der Wert $x$ ist dabei die geschätzte Weite deines Daumensprungs, $y$ spiegelt dann die daraus resultierende, geschätzte Distanz zu dem angepeilten Objekt wider. Das Verhältnis von Armlänge (große Strecke) zu Augenabstand (kleine Strecke) entspricht dann also dem Verhältnis von der Entfernung (große Strecke) zur Sprungweite (kleine Strecke).
Angenommen dein Daumen ist geschätzt $\pu{5 m}$ gesprungen, dann erhältst du:
$\pu{50 cm} : \pu{6 cm} = y: \pu{5 m}$
Schritt 6: Gleichung umstellen und ausrechnen
Im sechsten Schritt stellst du die Gleichung nach $y$ um und ermittelst deinen gesuchten Wert.
$\pu{50 cm} : \pu{6 cm} =y : \pu{5000 cm} ~\vert \cdot \pu{5000 cm}$
$y = \pu{50 cm} : \pu{6 cm} \cdot \pu{5000 cm}$
$y \approx \pu{41,67 m}$
Deine gesuchte Entfernung beträgt circa $\pu{41,67 m}$.
Kürzere Variante des Daumensprungs
Wenn es nicht so wichtig ist, dass du genau schätzt, kannst du eine verkürzte Version des Daumensprungs verwenden. Dabei gehst du davon aus, dass die Armlänge etwa das Zehnfache des Augenabstands beträgt.
Du kannst deshalb deine geschätzte Daumensprungweite einfach mit $10$ multiplizieren, um deine geschätzte Entfernung zu ermitteln.
$\text{Daumenspungweite} \cdot 10 = \text{geschätzte Entfernung}$
Diese Variante kann superhilfreich sein, wenn du z. B. im Wald oder in den Bergen einen Abstand schätzen möchtest und keine Hilfsmittel dabeihast.
Welche Fehlerquellen gibt es beim Daumensprung?
Eine wichtige Fehlerquelle beim Daumensprung ist eine falsche Schätzung bei der Daumensprungweite. Denn wenn du dich dabei beispielsweise um einen Meter verschätzt, weicht die gesuchte Entfernung am Ende zehn Meter von der tatsächlichen Entfernung ab.
Entfernungen mit dem Daumensprung abschätzen – Zusammenfassung
Mit dem Daumensprung kannst du im Gelände Entfernungen ohne Hilfsmittel abschätzen. Die Methode besteht aus sechs Schritten:
- Du streckst deinen Arm aus und stellst deinen Daumen auf.
- Du schließt ein Auge und peilst dein Ziel an.
- Du öffnest das Auge und schließt dein anderes Auge.
- Du schätzt die Entfernung des Daumensprungs.
- Du setzt die Werte in diese Gleichung ein: ${\text{Armlänge} : \text{Augenabstand} = \text{Distanz} : \text{Daumensprungweite}}$
- Du stellst die Gleichung um und rechnest deine geschätzte Entfernung aus.
In einer verkürzten Variante des Daumensprungs kannst du deine geschätzte Daumensprungweite auch einfach mit $10$ multiplizieren, um deine geschätzte Entfernung zu ermitteln.
$\text{Daumenspungweite} \cdot 10 = \text{geschätzte Entfernung}$
Strahlensätze – Entfernungen im Gelände Übung
-
Beschreibe, wie der Daumensprung durchgeführt wird.
TippsNehme deinen Daumen zu Hilfe und gehe die einzelnen Schritte durch.
Fällt dir dabei auf, dass dein Daumen gesprungen ist, wenn du das Ziel mit dem anderen Auge anpeilst?
LösungDer Daumensprung ist ein probates Mittel, um Strecken und Abstände abzuschätzen. Er ist dabei aber nur ein Bestandteil und du verwendest ihn stets in Verbindung mit dem 1. Strahlensatz. Hier wollen wir zunächst aber nur untersuchen, wie sich dieser Daumensprung durchführen lässt.
Zunächst gilt es, deinen Arm auszustrecken, eine Faust zu bilden und den Daumen aufzustellen. Diese Position muss jetzt für die nächsten Schritte gehalten werden, damit nicht schon durch Verwackeln des Armes Ungenauigkeiten entstehen. Nun schließt du ein Auge, zum Beispiel das rechte, und peilst mit dem geöffneten Auge dein Ziel an, sodass sich dein Daumen in einer Flucht mit dem angepeilten Gegenstand befindet. Nun wiederholst du diesen Vorgang, indem du mit dem anderen Auge dein Ziel anpeilst.
Wie du beim Ausprobieren vielleicht merkst, kommt es darauf an, welche Seite des entfernten Ziels du anpeilst. Mit ein bisschen Übung hast du aber sicherlich schnell den Dreh raus.
In jedem Fall fällt dir auf, dass dein Daumen gesprungen ist, nachdem du das Ziel mit dem anderen Auge angepeilt hast. Den Daumensprung schätzt du jetzt hinsichtlich des Ziels ab.
-
Ergänze den Weg zur Berechnung, wie weit Johnny vom Haus entfernt steht.
TippsÜberlege dir, welche Strecken zu den großen Strecken und welche zu den kleinen gezählt werden.
Wie kannst du die Gleichung nach der gesuchten Entfernung $y$ umstellen?
LösungJohnny möchte wissen, wie viele Meter er vom Haus entfernt steht. Er weiß, dass man mit dem Strahlensatz bestimmte Strecken zueinander in Beziehung setzen kann.
Bei unserer Aufgabe sind uns seine Armlänge sowie der Abstand seiner Augen bekannt. Mittels der Daumensprungmethode wird die Sprungweite $x$ des Daumens mit ungefähr $5~m$ abgeschätzt.
Nun stellt sich die Frage, wie man diese Strecken- und Abstandsangaben sinnvoll in Beziehung setzen kann, um am Ende die Entfernung y zu berechnen.
Da hilft uns der Strahlensatz weiter, den wir hier etwas vereinfacht benutzen können. Er lautet $\frac{\text{große Strecke}}{\text{kleine Strecke}} = \frac{\text{große Strecke}}{\text{kleine Strecke}}$.
Wichtig ist hierbei, dass wir von Anfang an wissen, was wir eigentlich berechnen wollen. Dann können wir die richtige Rechnung aufstellen, nämlich:
$\frac{\text{Armlänge}}{\text{Augenabstand}} = \frac{\text{Entfernung y}}{\text{Sprungweite x}}$
Setzen wir nun unsere Informationen in die Gleichung ein, ergibt sich $\frac{\text{50 cm}}{\text{6 cm}} = \frac{\text{y}}{\text{5 m}}$. Wir multiplizieren mit $5~m$, um nach $y$ aufzulösen und erhalten letztlich $y \approx 41,67~m$.
Da wir die Entfernung jedoch nur ungefähr abschätzen können, ist eine so präzise Angabe wie $41,67~m$ nicht unbedingt sinnvoll. Wir können einfach sagen, Johnnys Haus ist etwa $40$ Meter von ihm entfernt.
-
Bestimme die Strecke, in der Jimmy von den Bäumen entfernt steht.
TippsHalte dich an den Grundsatz $\frac{\text{große Strecke}}{\text{kleine Strecke}}$ = $\frac{\text{große Strecke}}{\text{kleine Strecke}}$.
Löse am Ende nach der gesuchten Strecke auf.
LösungDer Daumensprung ist manchmal eine nicht sehr genaue Methode zum Abschätzen von Strecken.
Diesmal kann Johnnys Bruder Jimmy allerdings das ideale Ergebnis des Daumensprungs mit dem 1. Strahlensatz berechnen, weil er weiß, in welcher Entfernung die beiden Bäume zueinander stehen. Diese Entfernung beträgt 12 Meter. Die gesuchte Strecke zwischen ihm und den Bäumen benennt er mit y.
Setzt er nun seine Informationen in die Gleichung ein, ergibt sich $\frac{\text{49 cm}}{\text{7 cm}}$ = $\frac{\text{y}}{\text{12 m}}$. Jetzt muss Jimmy nur noch nach y auflösen, indem er mit 12 m multipliziert.
Der Abstand zwischen ihm und den beiden Bäumen beträgt also y = 7 $\cdot$ 12 = 84 Meter.
-
Ermittle, wie weit du von Alia entfernt stehst.
TippsVerwende den 1. Strahlensatz, um die Lösung zu berechnen.
Löse nach der gesuchten Variablen auf.
LösungDas ist ein klassischer Falls, in dem du den 1. Strahlensatz verwenden kannst. Bedingung dafür ist allerdings, dass es zwei parallele Geraden gibt, die wie hier den Standort von Jule und Ahmed sowie von Hans und Alia verbinden.
Die Formel für die Berechnung lautet auch hier $\frac{\text{große Strecke}}{\text{kleine Strecke}}$ = $\frac{\text{große Strecke}}{\text{kleine Strecke}}$. Wir können die Entfernungen auch hier zueinander in Beziehung setzen, wobei der Name jeweils angibt, wie weit sie von dir entfernt stehen:
$\frac{\text{Jule}}{\text{Hans}}$ = $\frac{\text{Ahmed}}{\text{Alia}}$
Nun ist der größte Schritt getan. Wir müssen jetzt nur noch die jeweiligen Entfernungen in die Gleichung einsetzen. Dann können wir $\frac{60\text{m}}{45\text{m}}$ = $\frac{80\text{m}}{\text{Alia}}$ nach der Entfernung von Alia auflösen.
Alia steht 80 $\cdot \frac{45}{60}$ = 60 Meter von dir entfernt.
-
Benenne die richtigen Aussagen zum Daumensprung sowie zum 1. Strahlensatz.
TippsWie verhält sich deine Armlänge zum Abstand deiner Augen?
Gibt es Fehlerquellen beim Verwenden des Daumensprungs?
LösungDer Daumensprung ist eine Methode, um den Abstand eines in der Ferne liegenden Ziels einzuschätzen. Besitzt du keine modernen Hilfsgeräte, ist er allemal eine gute Alternative. Allerdings solltest du dir vor Augen führen, dass besonders große Entfernungen für Fehlerquellen sorgen, da bereits geringe Fehleinschätzungen andere Ergebnisse zur Folge haben.
Hatten wir für die Berechnung der Entfernung zum Haus bisher die Gleichung $\frac{50~cm}{6~cm}$ = $\frac{y}{5~m}$ aufgestellt und mit y $\approx$ 41,67 m gelöst, so ergibt sich ein ganz anderes Ergebnis, wenn wir die Sprungweite auf 7 Meter statt 5 Meter schätzen. $\frac{50~cm}{6~cm}$ = $\frac{y}{7~m}$ ergibt dann y $\approx$ 58,33 m. Das ergibt eine Differenz der Ergebnisse von fast 17 Metern. Es lassen sich mit dem Daumensprung also keine genauen Messungen durchführen, lediglich geschickte Abschätzungen sind möglich.
Als Faust- oder Daumenregel kannst du dir merken, dass die Armlänge ungefähr das Zehnfache des Augenabstands beträgt. Das spielt eine Rolle, wenn der Daumensprung in Zusammenhang mit dem 1. Strahlensatz verwendet wird.
Da der 1. Strahlensatz $\frac{\text{große Strecke}}{\text{kleine Strecke}}$ = $\frac{\text{große Strecke}}{\text{kleine Strecke}}$ lautet, kannst du bei Verwendung des Daumensprungs die linke Seite der Gleichung durch 10 ersetzen, da ja $\frac{\text{Armlänge}}{\text{Augenabstand}} \approx$ 10.
-
Bestimme, in welcher Distanz x der Ball von Marie entfernt liegt.
TippsBerücksichtige, dass du den 1. Strahlensatz kurz als $\frac{\text{große Strecke}}{\text{kleine Strecke}}$ = $\frac{\text{große Strecke}}{\text{kleine Strecke}}$ formulieren kannst.
Die Entfernung von Ball zu Mauer ist um 2 Meter kürzer als die Entfernung, in der Marie vom Ball steht.
Löse die Brüche auf, indem du mit den Nennern multiplizierst.
LösungAuch diese Aufgabe beinhaltet eine Variante des $1.$ Strahlensatzes. Wie du siehst, ist er vielfältig anwendbar.
Hier stehen die beiden Parallelen des Dreiecks in einem Verhältnis, so wie auch die Entfernung Maries zum Ball und die Teilstrecke zwischen Ball und Mauer in Verhältnis stehen.
In einer mathematischen Gleichung verpackt, könnte das so aussehen:
$\frac{\text{Augenhöhe Marie}}{\text{Höhe der Mauer}}$ = $\frac{\text{x}}{\text{Entfernung Ball zu Mauer}}$
Auf der linken Seite steht $\frac{\text{1,60 m}}{\text{1,20 m}}$ = $\frac{\text{4}}{\text{3}}$.
Die rechte Seite ist etwas schwieriger, da wir beide Angaben nicht haben. Allerdings wissen wir, dass Marie $2$ Meter von der Mauer entfernt steht. Das hilft uns weiter, wie wir gleich sehen werden. Dann können wir die rechte Seite nämlich durch $\frac{\text{x}}{\text{x - 2}}$ beschreiben.
Nun müssen wir nur noch ein bisschen rechnen:
$\frac{\text{4}}{\text{3}}$ = $\frac{\text{x}}{\text{x - 2}}$
Dazu multiplizieren wir mit $x - 2$ und erhalten $\frac{4}{3}\cdot x - \frac{8}{3} = x$ bzw. $\frac{1}{3}\cdot x = \frac{8}{3}$ und somit $x = 8$.
Die Entfernung zwischen Marie und Mauer beträgt $8$ Meter.
9.918
sofaheld-Level
6.600
vorgefertigte
Vokabeln
8.312
Lernvideos
38.646
Übungen
33.706
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Klassenstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung


 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?