Erster Strahlensatz – Einführung


in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
Grundlagen zum Thema Erster Strahlensatz – Einführung
Nach dem Schauen dieses Videos wirst du in der Lage sein, in einer Strahlensatzfigur die Länge einer fehlenden Strecke unter Anwendung des ersten Strahlensatzes zu berechnen.
Zunächst lernst du, dass in einer Strahlensatzfigur die Verhältnisse einander entsprechender Strecken gleich groß sind. Anschließend siehst du, wie du ausgehend von dieser Eigenschaft den ersten Strahlensatz formulieren kannst. Abschließend lernst du, wie du unter Anwendung des ersten Strahlensatzes eine fehlende Strecke einer Strahlensatzfigur berechnen kannst.
Lerne etwas über den ersten Strahlensatz, indem du Ray dem verliebten Flughörnchen bei der Berechnung seiner Flugbahn hilfst.
Das Video beinhaltet Schlüsselbegriffe, Bezeichnungen und Fachbegriffe wie erster Strahlensatz, Strahlensatzfigur, Verhältnis, Strecken, parallele Strecken und sich schneidende Strecken.
Bevor du dieses Video schaust, solltest du bereits wissen, wie du Bruchgleichungen umstellst.
Nach diesem Video wirst du darauf vorbereitet sein, den zweiten Strahlensatz zu lernen.
Transkript Erster Strahlensatz – Einführung
Ray, das verliebte Flughörnchen, möchte seine Angebetete Amanda mit seinen Flugkünsten beeindrucken! Die ist leider nicht so begeistert. Das liegt wohl daran, dass Rays letzter Flugversuch gründlich danebengegangen ist. Aber jetzt will Ray es besser machen und genau bei ihr landen. Aber aus welcher Höhe des Baumes muss er starten, um elegant zu ihr hinüberzugleiten? Das finden wir für Ray heraus mit dem ersten Strahlensatz! Sehen wir uns die Situation noch einmal genauer an! Die Kante des Baums und die Bodenlinie können wir in der Skizze als Strahlen darstellen, denn sie sind gerade Linien mit einem Anfangspunkt Z. Amanda sitzt 16 Meter vom Baum entfernt. Die Länge dieser Strecke von der Baumwurzel bis zu Rays ungenügender Landestelle beträgt 10 Meter und Rays erster Versuch startete aus einer Höhe von 5 Metern auf dem Baum. Jetzt sieh dir mal Rays Flugbahnen genauer an! Das geübte Flughörnchen gleitet immer mit demselben Gefälle. Deshalb haben die Flugbahnen überall den gleichen Abstand zueinander und schneiden sich nicht. Sie sind also Parallelen. Die gesamte Figur wird auch als Strahlensatzfigur bezeichnet. Sie besteht aus zwei Strahlen, die von einem gemeinsamen Punkt Z – dem Scheitel – ausgehen und aus zwei Parallelen, die diese Strahlen schneiden. Und was nützt dir diese Figur? Ray will ja wissen, von welchem Punkt aus er starten muss. In einer Strahlensatzfigur kannst du die Länge einer fehlenden Strecke ausrechnen, wenn du drei andere kennst. In einer Strahlensatzfigur gilt, dass die Verhältnisse einander zugehöriger Strecken gleich groß sind. Hier bei uns ist das Verhältnis der beiden Abflughöhen gleich dem Verhältnis der Entfernung von Z zu den Landepunkten. Beim ersten Strahlensatz suchen wir immer Verhältnisse von Strecken entlang der Strahlen. Mathematisch kannst du ein Verhältnis als Bruch aufschreiben. Dazu beschriften wir die übrigen Punkte in der Strahlensatzfigur mit den Bezeichnungen A1, A2, B1 und B2. Die Strecken nennen wir dann 'ZA1', 'ZA2', 'ZB1' und 'ZB2'. Rechnen wir also aus, wie hoch Ray auf den Baum klettern muss - das ist die Strecke 'ZB2'. Wir beginnen mit der gesuchten Strecke und suchen dann die ihr zugehörige Strecke auf demselben Strahl. Das Verhältnis dieser beiden Strecken entspricht dem Verhältnis der zugehörigen Strecken auf dem anderen Strahl. Die Strecke 'ZB2' geteilt durch die Strecke 'ZB1' ist gleich der Strecke 'ZA2' geteilt durch die Strecke 'ZA1'. Jetzt können wir die entsprechenden Werte einsetzen ZB2 lassen wir stehen, denn das ist ja die gesuchte Strecke und setzen für ZB1 fünf, für ZA2 sechzehn und für ZA1 zehn ein. Diese Gleichung lösen wir jetzt nach 'ZB2' auf, also multiplizieren wir beide Seiten mit 5 Metern jetzt haben wir 'ZB2' gleich 16 Meter mal 5 Meter durch 10 Meter hier können wir diese beiden Einheiten "Meter" kürzen also bleibt achtzig Meter durch zehn und wir erhalten acht Meter. Das heißt, Ray muss aus 8 Metern Höhe starten! Solange Ray auf den Baum kraxelt, schauen wir uns noch ein zweites Beispiel an: Auch diese Figur ist eine Strahlensatzfigur. Anstelle der Strahlen haben wir hier zwei Geraden, die sich in einem Punkt schneiden. Und die Parallelen, die diese Geraden schneiden, befinden sich auf beiden Seiten des Schnittpunkts. Hier gilt der erste Strahlensatz aber ebenfalls. Aber Vorsicht: die einander zugehörigen Strecken befinden sich jeweils auf derselben Geraden. Wenn du also zum Beispiel wissen möchtest, wie lang die Strecke "ZA1" ist, notierst du Z A 1 zu Z A 2 gleich Z B 1 zu Z B 2. Mit den Werten aus der Zeichnung können wir die Länge der Strecke 'ZA1' bestimmen: Dazu setzen wir für Z A 2 drei, für Z B 1 acht und für Z B 2 vier in die Rechnung ein. Das rechnen wir jetzt aus auf beiden Seiten mal drei das ergibt 8 mal 3 durch 4 das kannst du kürzen und die gesuchte Länge ist 6. Wir fassen zusammen: Wenn zwei Strahlen von Parallelen geschnitten werden, handelt es sich um eine Strahlensatzfigur. Beim ersten Strahlensatz bilden wir Verhältnisse zugehöriger Seiten in so einer Strahlensatzfigur. Damit kannst du die Länge einer Strecke bestimmen, wenn du die übrigen Strecken gegeben hast. Mit dem Strahlensatz kannst du gut Größen oder Entfernungen ausrechnen. Du kannst dir immer merken: "Lang zu kurz" verhält sich wie "lang zu kurz". Er gilt auch, wenn anstatt Strahlen zwei Geraden von Parallelen geschnitten werden. So Ray, jetzt gilt's! Guten Flug!
Erster Strahlensatz – Einführung Übung
-
Bestimme die korrekten Aussagen zum ersten Strahlensatz.
TippsSo kann eine Strahlensatzfigur aussehen.
Eine Summe ist das Ergebnis einer Addition.
LösungDiese Aussagen sind falsch:
„Kennst du zwei Längen der Strahlensatzfigur, kannst du die letzte Strecke ausrechnen.“
- Um eine fehlende Länge der Strahlensatzfigur auszurechnen, müssen drei Längen gegeben sein.
- Mit einer Strahlensatzfigur kannst du eine Verhältnisgleichung zugehöriger Strecken aufstellen. Das ist eine Gleichung, die aus zwei Quotienten (das Ergebnis einer Division) besteht. Eine Summe ist das Ergebnis einer Addition.
„Schneiden zwei Parallelen zwei Strahlen, die denselben Anfangspunkt besitzen, kannst du die Strahlensätze anwenden.“
- So kann eine Strahlensatzfigur aussehen.
- Dies ist eine weitere Möglichkeit für eine Strahlensatzfigur.
Du musst jedoch immer die zwei größeren durch die beiden kleineren Längen oder die zwei kleineren durch die beiden größeren Längen teilen.“
$~$
- Die folgende Kombination ist nicht möglich: $\dfrac{\text{Lang}}{\text{Kurz}}=\dfrac{\text{Kurz}}{\text{Lang}}$
-
Bestimme die Länge mithilfe des ersten Strahlensatzes.
TippsEine Verhältnisgleichung besteht aus zwei Quotienten, die gleichgesetzt werden.
Hast du die Verhältnisgleichung aufgestellt, musst du die gegebenen Längen einsetzen und nach der gesuchten Länge auflösen.
LösungDu kannst die Rechnung so vervollständigen:
Zuerst stellt Ray eine Verhältnisgleichung auf. Er weiß, dass er dafür jeweils zwei Längen auf demselben Strahl durch einander teilen und anschließend die beiden Verhältnisse gleichsetzen muss.
- In der Mathematik ist ein Verhältnis der Quotient zweier Zahlen. Eine Verhältnisgleichung besteht aus zwei Quotienten, die gleichgesetzt werden.
$\dfrac{\overline{ZB_2}}{\overline{ZB_1}}$
Das entsprechende Verhältnis auf dem rechten Strahl lautet:
$\dfrac{\overline{ZA_2}}{\overline{ZA_1}}$
Die Verhältnisgleichung lautet also:
$\dfrac{\overline{ZB_2}}{\overline{ZB_1}}=\dfrac{\overline{ZA_2}}{\overline{ZA_1}}$
- Hier musst du darauf achten, dass du die Verhältnisse richtig aufstellst. Du musst entweder zweimal die längere Strecke durch die kürzere Strecke teilen und gleichsetzen oder zweimal die kürzere Strecke durch die längere Strecke. Du darfst sie allerdings nie vermischen. Es gilt also:
$\qquad \dfrac{\overline{ZB_2}}{\overline{ZB_1}}=\dfrac{\overline{ZA_2}}{\overline{ZA_1}}$
$\qquad \dfrac{\overline{ZB_2}}{\overline{ZB_1}} \neq \dfrac{\overline{ZA_1}}{\overline{ZA_2}}$
Hier kann er die gegebenen Längen einsetzen:
$\dfrac{\overline{ZB_2}}{5~\text{m}}=\dfrac{16~\text{m}}{10~\text{m}}$ (...)
$\Leftrightarrow ~\overline{ZB_2}=8~\text{m}$
- Hast du die Verhältnisgleichung aufgestellt, musst du die gegebenen Längen einsetzen und nach der gesuchten Länge auflösen.
-
Ermittle die korrekten Aussagen zu dieser Strahlensatzfigur.
TippsEine mögliche Verhältnsigleichung lautet:
$\dfrac{\overline{ZB_2}}{\overline{ZB_1}}=\dfrac{\overline{ZA_2}}{\overline{ZA_1}}$.
Diese Gleichung kannst du durch Äquivalenzumformungen umformen.
Die Längen der Verhältnisgleichung kannst du berechnen, indem du sie in obige Gleichung einsetzt und nach der gesuchten Länge umformst.
LösungDiese Aussagen sind falsch:
„Eine Verhältnisgleichung könnte so aussehen:
$\dfrac{\overline{ZB_1}}{\overline{ZB_2}}=\dfrac{\overline{ZA_2}}{\overline{ZA_1}}$“
„Um die Verhältnisgleichung aufzustellen, musst du Längen auf unterschiedlichen Geraden durch einander teilen und gleichsetzen. Damit ergibt sich beispielsweise:
$\dfrac{\overline{ZB_2}}{\overline{ZA_1}}=\dfrac{\overline{ZA_2}}{\overline{ZB_1}}$“
- Um eine Verhältnisgleichung aufzustellen, kannst du jeweils die längere durch die kürzere Strecke auf derselben Geraden teilen und die beiden Quotienten gleichsetzen. Die aufgestellte Gleichung kannst du durch Äquivalenzumformungen umformen. Dadurch erhältst du aber keine der oben angegebenen Verhältnisgleichungen. Eine mögliche Gleichung lautet nämlich wie folgt:
„Sind die Längen $\overline{ZB_2}=4$, $\overline{ZA_1}=3$ und $\overline{ZB_1}=8$ gegeben, ergibt sich: $\overline{ZA_2}=6$“
- Setzt du diese Längen in die obige Verhältnisgleichung ein und stellst um, dann erhältst du: $\overline{ZA_2}=\frac{4}{8} \cdot 3= \frac{3}{2}$
„Sind die Längen $\overline{ZB_2}=4$, $\overline{ZA_2}=3$ und $\overline{ZB_1}=8$ gegeben, ergibt sich: $\overline{ZA_1}=6$“
- Durch das Anwenden obiger Verhältnisgleichung erhältst du: $\overline{ZA_1}=\frac{8}{4} \cdot 3 =6$
- Dieser Fall tritt in unserem Beispiel auf. Auch hier kannst du die Strahlensätze anwenden.
-
Ermittle die Längen mithilfe des ersten Strahlensatzes.
TippsSo kann eine Strahlensatzfigur aussehen.
Mit dem ersten Strahlensatz kannst du folgende Verhältnisgleichung bestimmen und passend umformen:
$\dfrac{\overline{ZB_2}}{\overline{ZB_1}}=\dfrac{\overline{ZA_2}}{\overline{ZA_1}}$
LösungMit dem ersten Strahlensatz kannst du folgende Verhältnisgleichung bestimmen und passend umformen:
$\dfrac{\overline{ZB_2}}{\overline{ZB_1}}=\dfrac{\overline{ZA_2}}{\overline{ZA_1}}$
Damit erhältst du folgende Längen:
- $\overline{ZA_2}= \dfrac{\overline{ZB_2}}{\overline{ZB_1}} \cdot \overline{ZA_1} = \frac{8}{4} \cdot 5=10$
- $\overline{ZB_2}=\frac{1}{2}$
- $\overline{ZA_1}= \dfrac{\overline{ZB_1}}{\overline{ZB_2}} \cdot \overline{ZA_2}= \dfrac{1}{\frac{1}{3}} \cdot 6= 3 \cdot 6=18$
- $\overline{ZB_1}=6$
-
Beschrifte die Strahlensatzfigur.
TippsEine Streckenbezeichnung besteht immer aus dem Anfangs- und Endpunkt. Darüber zeichnest du einen Strich. Zum Beispiel verläuft die Strecke $ \overline{A_2 B_2}$ zwischen den Punkten $A_2$ und $B_2$.
Parallelen haben überall den gleichen Abstand zueinander.
LösungSo kannst du die Strahlensatzfigur vervollständigen:
- Eine Streckenbezeichnung besteht immer aus dem Anfangs- und Endpunkt. Darüber zeichnest du einen Strich. Zum Beispiel: $ \overline{ZA_2}$
- Die Bezeichnung der Punkte kannst du genauso aus den Streckenbezeichnungen erkennen. $ \overline{ZA_2}$ verläuft zwischen den Punkten $Z$ und $A_2$
- Strahlen sind Linien mit einem Anfangs- und keinem Endpunkt. Hier abgebildet sind zwei Strahlen, die aus dem gemeinsamen Punkt $Z$ entspringen. Parallelen haben überall den gleichen Abstand zueinander.
-
Leite ab, warum du den ersten Strahlensatz auf verschiedene Strahlensatzfiguren anwenden kannst.
TippsIn einer Punktspiegelung bleiben die Längen zwischen den Ursprungspunkten und dem Spiegelzentrum erhalten. Der gespiegelte Punkt hat also den gleichen Abstand zum Spiegelzentrum wie der ursprüngliche Punkt.
Die klassische Strahlensatzfigur besteht aus zwei Strahlen, die dem gleichen Punkt $Z$ entspringen, welche von zwei parallelen Geraden geschnitten werden.
LösungDiese Aussagen sind falsch:
„Spiegelst du die Punkte $A_2$ und $B_2$ an einer Achse, die parallel zu den beiden Parallelen liegt, dann erhältst du die Punkte $A_2'$ und $B_2'$.“
- Die Punkte $A_2'$ und $B_2'$ erhältst du durch eine Punktspiegelung der Punkte $A_2$ und $B_2$ an $Z$.
- Das würde nicht funktionieren, da diese Geraden in der Strahlensatzfigur parallel sein müssen. Das ist nicht gegeben, wenn sie sich schneiden.
„Sind jeweils die Strecken $\overline{ZA_2}$ und $\overline{ZA_2'}$ sowie $\overline{ZB_2}$ und $\overline{ZB_2'}$ gleich lang, ist die Gerade durch $A_2$ und $B_2$ parallel zu der Geraden durch $A_2'$ und $B_2'$.“
- Sind diese Längen gleich lang, erfüllen sie den ersten Strahlensatz. Deshalb muss auch die Gerade durch $A_2$ und $B_2$ parallel zur Geraden durch $A_2'$ und $B_2'$ sein.
„Führst du eine Punktspiegelung der Punkte $A_1$ und $B_1$ an $Z$ durch, kannst du den ersten Strahlensatz auch auf die Figur bestehend aus den neu entstandenen Punkten $A_1'$ und $B_1'$ und den Punkten $A_2$ und $B_2$ anwenden.“
- Durch diese Punktspiegelung erhältst du auf der linken Seite von $Z$ eine Strahlensatzfigur, die punktsymmetrisch zu der auf der rechten Seite ist. Auf beiden Seiten kannst du die Strahlensätze anwenden.
9.957
sofaheld-Level
6.600
vorgefertigte
Vokabeln
8.313
Lernvideos
38.641
Übungen
33.706
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Klassenstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung




 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?




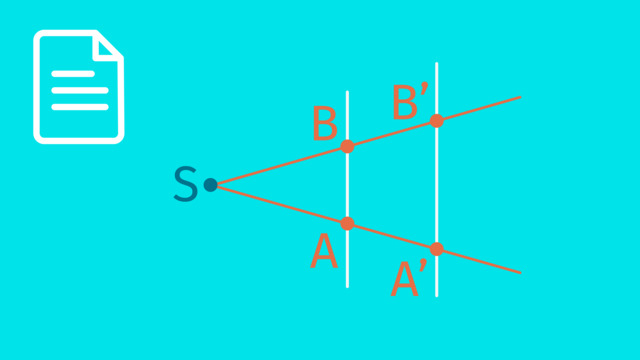









Hallo Arda, vielen Dank für deine Frage! Du hast die Varianten des ersten Strahlensatzes richtig aufgezählt. Diese kann man aber auch immer nochmal umstellen. In diesem Video wird jeweils der Kehrwert genutzt. Das ändert aber nichts an dem Ergebnis. Bei deiner ersten Rechnung ist ein kleiner Denkfehler drin: Um 5/SA' = 10/16 nach SA' aufzulösen, müssen wir erst mit SA' multiplizieren und dann mit 16/10. So kommen wir auch auf das Ergebnis 8. Ich hoffe, wir konnten dir weiterhelfen. Liebe Grüße aus der Redaktion!
Im Video "Strahlensätze" werden drei erste Strahlensätze genannt. SA/SA' = SB/SB' und SA/AA' = SB/BB' und SA'/AA' = SB'/BB'. Demnach muss man in diesem Video den ersten Strahlensatz wählen, da SA' gesucht wird. Daraus ergibt sich: 5/SA' = 10/16 -> Auflösen, um 5 Mal zu nehmen -> 10/16 * 5 = SA' -> 3,125 m. In diesem Video wird allerdings eine andere Formel benutzt, wo man nicht 10/16 + 5 sondern 16/10 * 5 rechnet, um auf 8m zu kommen. Wieso ist das so? Ich dachte, es gibt drei erste Strahlensätze und zwei zweite Strahlensätze wie im vorherigen Video erwähnt. Die im Video hat allerdings die Buchstaben vertauscht.
Die erkärung war ok.
In der Schule wurde es viel komplizierter erklärt. So ist es viel einfacher zu verstehen. Habe es direkt verstanden.
Hallo Doranpijo01,
vielleicht hast du momentan Verbindungsprobleme mit dem Internet. Hast du schon ausprobiert, die Seite neu zu laden?
Wenn du aber weiterhin technische Probleme beim Abspielen der Videos haben solltest, kannst du dich gerne an unseren Support unter support@sofatutor.com wenden. Sie werden dir dann weiterhelfen.
Liebe Grüße aus der Redaktion