Erweiterung der Strahlensätze
in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
5 Minuten verstehen
5 Minuten üben
2 Minuten Fragen stellen
Bereit für eine echte Prüfung?
Grundlagen zum Thema Erweiterung der Strahlensätze
Nach dem Schauen dieses Videos wirst du in der Lage sein, die Erweiterung der Strahlensätze anzuwenden.
Zunächst lernst du, wie du dir die Erweiterung der Strahlensätze mit Hilfe einer Punktspiegelung verdeutlichen kannst. Anschließend werden dir der erste und zweite erweiterte Strahlensatz vorgestellt. Abschließend lernst du an einigen Beispielen, wie du diese anwenden kannst.
Lerne, wie du die erweiterten Strahlensätze anwendest, indem du den Astronomen Christiaan Huygens unterstützt.
Das Video beinhaltet Schlüsselbegriffe, Bezeichnungen und Fachbegriffe wie erweiterte Strahlensätze, Punktspiegelung, parallele Geraden, sich schneidende Geraden, Verhältnis, erster und zweiter Strahlensatz.
Bevor du dieses Video schaust, solltest du bereits wissen, wie die Strahlensätze formuliert sind und was eine Punktspiegelung ist.
Nach diesem Video wirst du darauf vorbereitet sein, dein Wissen zu den Strahlensätzen zu vertiefen.
Transkript Erweiterung der Strahlensätze
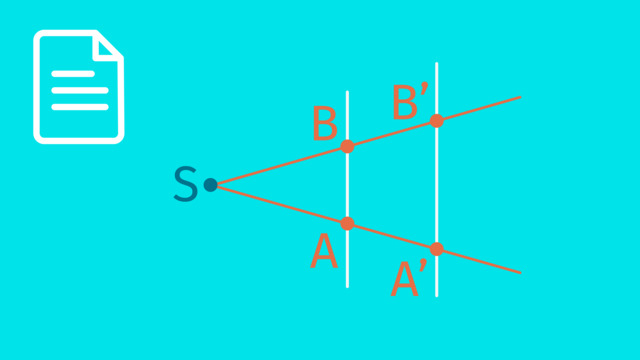
Wir sind in den Niederlanden vor etwa 400 Jahren und treffen den Astronomen Christiaan Huygens. Er kann mit selbst geschliffenen Linsen die Teleskope jener Zeit deutlich verbessern. Und damit erkennt er als Erster, dass der Saturn Ringe besitzt. Sein neues Teleskop kann den Saturn nämlich besonders stark vergrößern. Nun fragt er sich, WIE groß die Ringe sind. Er beginnt zu rechnen und benötigt dafür die Erweiterung der Strahlensätze. Für eine Zeichnung im richtigen Maßstab ist der Saturn einfach zu weit weg. Aber ungefähr so könnte man das Ganze skizzieren: Hier ist der Saturn, von dem aus das Licht in das Teleskop fällt. Und dahinter liegt das Bild, das das Teleskop erzeugt. In Wirklichkeit verlaufen die Lichtstrahlen im Teleskop "etwas" komplizierter. Aber das muss uns hier nicht weiter interessieren. Stellen wir die Größen des Saturns und seines Bildes als Strecken entlang zweier paralleler Geraden dar, erhalten wir diese Figur. Die beiden Parallelen werden von zwei Geraden geschnitten, die selber einen gemeinsamen Schnittpunkt haben. Diesen Schnittpunkt nennen wir Scheitelpunkt S. Erinnert dich diese Figur an etwas? Sie wirkt ein Wenig wie eine Strahlensatzfigur. Damit wir einen Strahlensatz anwenden dürfen, müssten doch beide Parallelen auf der gleichen Seite von S liegen, oder? Kein Problem: Führen wir doch eine Punktspiegelung des Saturnbildes am Punkt S durch. Dann landen alle Streckenabschnitte auf der gleichen Seite von S. Bei dieser Figur können wir den Strahlensatz anwenden! Die gesuchte Größe ist der Durchmesser der Saturnringe, wir bezeichnen sie mit 'x'. Die zugehörige Strecke ist die Größe des Bildes, die wir mit 'b' bezeichnen wollen. 'x' und 'b' verhalten sich zueinander wie die zugehörigen Strecken auf den entsprechenden Strahlen: Zum Saturn gehört die Strecke 'L1' zum Bild des Saturns die Strecke 'L2'. Der zweite Strahlensatz besagt nun: 'x' zu 'b' verhält sich wie 'L1' zu 'L2'. Nach einer Umformung erhalten wir diese Gleichung für 'x'. Würde die Gleichung auch gelten, wenn wir zuvor nicht punktspiegeln? Und da sich beim Punktspiegeln die Längen der Seiten nicht ändern, gilt der Strahlensatz also auch in der ursprünglichen Figur, wenn der Scheitelpunkt zwischen den Parallelen liegt. Wo liegen nun die einander zugehörigen Strecken? Die Strecken entlang eines Strahls, also zum Beispiel diese und diese, liegen nun auf derselben Geraden – Hier und hier. Schauen wir uns das doch mal an einem Beispiel an. In der Skizze siehst du die beiden parallelen Strecken 'A1 B1' und gegenüber 'A2 B2'. Wir kennen die Länge der Strecke 'A1 B1', sie beträgt 5 Längeneinheiten. Auf der gleichen Seite wie 'A1 B1' verläuft vom Scheitel ausgehend die Strecke 'S A1' mit 7 Längeneinheiten. Und auf der gegenüberliegenden Seite und derselben Geraden liegt die Strecke 'S A2', die 14 Längeneinheiten misst. Entlang der Parallelen auf dieser Seite verläuft die Strecke 'A2 B2', deren Länge gesucht ist. Wir berechnen sie mit dem zweiten Strahlensatz, indem wir sie in das Verhältnis mit der gegenüberliegenden Strecke 'A1 B1' setzen. Das entsprechende Verhältnis aus 'S A2' und 'S A1' ist genauso groß. Wir setzen die gegebenen Längen ein und schreiben die Verhältnisse als Brüche – das geht immer. Nun stellen wir nach 'A2 B2' um und erhalten so als Länge der Strecke 'A2 B2': 10 Längeneinheiten. Hier haben wir den zweiten Strahlensatz benutzt. Genauso gilt auch der erste Strahlensatz, wenn der Scheitelpunkt zwischen den Parallelen liegt. Lass uns das an einem Beispiel überprüfen. Wir wollen die Länge der Strecke SA1 bestimmen. Die ihr zugehörige Strecke ist SA2, da SA1 und SA2 auf derselben Geraden liegen. Wir setzen sie miteinander ins Verhältnis. Die Strecke 'S B1' hat eine Länge von 12 und 'S B2' von 7 Längeneinheiten. Die Strecke 'S B1' gehört im Strahlensatz zur Strecke 'S B2', weil sie beide wiederum auf derselben Geraden liegen. Nach dem ersten Strahlensatz sind die beiden Verhältnisse gleich groß. Wir berechnen die Länge der Strecke 'S A1', setzen dazu die bekannten Werte ein machen aus der Verhältnisgleichung eine Bruchgleichung und stellen die Gleichung um. Die Strecke SA1 muss also circa 10,3 Längeneinheiten lang sein. Wir fassen zusammen: Beide Strahlensätze gelten auch dann, wenn der Scheitelpunkt zwischen den Parallelen liegt. Übrigens nennen wir sie dennoch Strahlensätze, obwohl die Parallelen jetzt von geraden statt von Strahlen geschnitten werden. Die Strahlensätze gelten, weil wir sie durch eine Punktspiegelung auf die herkömmlichen Strahlensätze zurückführen können und sich dabei die Längen der Strecken nicht ändern. Um die einander zugehörigen Strecken zu finden, merken wir uns: Beim ersten Strahlensatz liegen die Strecken auf derselben Geraden jeweils zusammen. Beim zweiten Strahlensatz gehören die Strecken auf nur einer der beiden Geraden zusammen und die beiden auf den Parallelen. Christiaan Huygens konnte somit bestimmen, dass die Ringe des Saturns im Durchmesser etwa 270.000 Kilometer groß sind. Und damit schlägt er Kapital aus seinem neuen Teleskop und verkauft einen kurzen Blick in die Weiten des Weltalls zu strahlenden Preisen.
Erweiterung der Strahlensätze Übung
-
Bestimme die korrekten Aussagen zur Erweiterung der Strahlensätze.
TippsHier liegt der Schnittpunkt der Geraden zwischen den Parallelen.
Der erste Strahlensatz der obigen Zeichnung lautet:
$\dfrac{\overline{ S A_1 }}{\overline{S A_2}}=\dfrac{\overline{ S B_1 }}{\overline{S B_2}}$.
LösungDiese Aussagen sind falsch:
„Die Strahlensätze kannst du nur anwenden, wenn die Parallelen auf der gleichen Seite des Schnittpunkts $S$ der sich schneidenden Geraden liegen.“
- Auch hier kannst du die bekannten Strahlensätze anwenden. Du kannst die Figur nämlich durch eine Punktspiegelung auf die ursprüngliche zurückführen.
- Der zweite Strahlensatz enthält die Längen der Parallelen, die zwischen den sich schneidenden Geraden liegen. Du kannst damit also auch diese berechnen.
„Die Rechnung des ersten Strahlensatzes kannst du aufstellen, indem du jeweils die Längen, die auf derselben Geraden liegen, ins Verhältnis setzt.“
„Eine Verhältnisgleichung kannst du immer in eine Bruchgleichung umschreiben.“
- Mit Bruchgleichungen lässt sich viel besser rechnen. Wenn möglich, solltest du deine Gleichungen so umschreiben.
-
Berechne die Länge mit dem zweiten Strahlensatz.
TippsFührst du eine Punktspiegelung einer geometrischen Figur durch, bleiben sämtliche Längen der Figur erhalten.
Mit dem zweiten Strahlensatz kannst du jeweils die Strecken auf den Parallelen sowie die Strecken auf den sich schneidenden Geraden ins Verhältnis setzen. Anschließend setzt du die Verhältnisse gleich.
LösungDen Lückentext kannst du so vervollständigen:
Zwei Parallelen schneiden zwei weitere, sich schneidende Geraden. Du kannst die Strahlensätze auch anwenden, wenn der Schnittpunkt der sich schneidenden Geraden zwischen den Parallelen liegt. Das kannst du dir mit einer Punktspiegelung veranschaulichen.
- Eine Punktspiegelung erhält die Längen einer Figur. Deshalb kannst du auch hier die Strahlensätze anwenden.
$\overline{A_2 B_2}:\overline{A_1 B_1}=\overline{ S A_2 }:\overline{S A_1}$.
- Hier wendest du den zweiten Strahlensatz an. Dabei setzt du jeweils die Strecken auf den Parallelen ($\overline{A_2 B_2}$ und $\overline{A_1 B_1}$) sowie die Strecken auf den sich schneidenden Geraden ($\overline{ S A_2 }$ und $\overline{S A_1}$) ins Verhältnis. Anschließend setzt du die Verhältnisse gleich.
$\frac{\overline{A_2 B_2}}{5}=\frac{14}{7}$.
Und nach der gesuchten Größe umstellen und ausrechnen:
$\overline{A_2 B_2}= 5 \cdot \frac{14}{7}=10$.
Die gesuchte Länge ist also $10$ Längeneinheiten lang.
- Nachdem du die Gleichung aufgestellt hast, kannst du die gesuchte Größe bestimmen.
-
Erschließe die korrekten Aussagen.
TippsIn dieser Figur kannst du die Strahlensätze anwenden, da du die Figur punktspiegeln kannst.
Den ersten Strahlensatz kannst du zum Beispiel so ausdrücken:
$\dfrac{\overline{S B_1 }}{\overline{S B_2 }}=\dfrac{\overline{S A_1 }}{\overline{S A_2 }}$.
Diese Gleichung kannst du zudem durch Äquivalenzumformungen umformen.
LösungDiese Aussagen sind falsch:
„Mit dem ersten Strahlensatz kannst du $\overline{ A_2 B_2}=25$ bestimmen.“
Das Ergebnis ist korrekt, allerdings wird hier der zweite Strahlensatz angewandt. $\overline{A_2 B_2}= \dfrac{\overline{ S A_2 }}{\overline{S A_1}} \cdot \overline{A_1 B_1}=\dfrac{30}{60} \cdot 50= 25$
„Nach einer Punktspiegelung liegen die Punkte $A_1$ und $B_2$ auf einer Geraden.“
Nach einer Punktspiegelung liegen jeweils die Punkte $A_1$ und $A_2$ sowie die Punkte $B_1$ und $B_2$ auf einer Geraden. Deshalb kannst du hier die Strahlensätze anwenden.
Diese Aussagen sind korrekt:
„Das Verhältnis $\dfrac{\overline{S B_1 }}{\overline{S B_2 }}$ beträgt $2$.“
Mit dem ersten Strahlensatz kannst du die Verhältnisse $\dfrac{\overline{S B_1 }}{\overline{S B_2 }}=\dfrac{\overline{S A_1 }}{\overline{S A_2 }}$ angeben. Setzt du hier $\overline{S A_1 }=60$ sowie $\overline{S A_2 }=30$ und kürzt, erhältst du das angegebene Verhältnis.
„Der erste Strahlensatz besagt: $\dfrac{\overline{S B_2 }}{\overline{S B_1 }}=\dfrac{\overline{S A_2 }}{\overline{S A_1 }}$.“
Den ersten Strahlensatz kannst du auf verschiedene Arten ausdrücken. Durch Äquivalenzumformungen kannst du $\dfrac{\overline{S B_1 }}{\overline{S B_2 }}=\dfrac{\overline{S A_1 }}{\overline{S A_2 }}$ in obiges Ergebnis umformen.
„Um die fehlende Parallele zu bestimmen, musst du das Ergebnis von $\dfrac{30}{60} \cdot 50$ bestimmen.“
Formst du den zweiten Strahlensatz $ \dfrac{\overline{A_2 B_2}}{\overline{A_1 B_1}}= \dfrac{\overline{ S A_2 }}{\overline{S A_1}}$ um, erhältst du: $\overline{A_2 B_2}= \dfrac{\overline{ S A_2 }}{\overline{S A_1}} \cdot \overline{A_1 B_1}=\dfrac{30}{60} \cdot 50= 25$.
-
Bestimme die Längen mit den Strahlensätzen.
TippsSo kann der zweite Strahlensatz lauten:
$\dfrac{\overline{A_2 B_2}}{\overline{A_1 B_1}}=\dfrac{\overline{ S A_2 }}{\overline{S A_1}}$.
$\dfrac{\overline{S B_2 }}{\overline{S B_1 }}=\dfrac{\overline{S A_2 }}{\overline{S A_1 }}$
Das ist ein möglicher erster Strahlensatz.
LösungUm die Paare zu verbinden, musst du die Strahlensätze anwenden. Der erste Strahlensatz kann lauten:
$\dfrac{\overline{S B_2 }}{\overline{S B_1 }}=\dfrac{\overline{S A_2 }}{\overline{S A_1 }}$.
Setzt du hier $\overline{ S B_2 }=3$, $\overline{ S A_2 }=1$ und $\overline{ S A_1 }=3$ und formst um, erhältst du:
- $\overline{ S B_1 }=\overline{ S B_2 } \cdot \frac{\overline{ S A_1 }}{\overline{ S A_2 }}= 3 \cdot \frac{3}{1}=9$.
$\dfrac{\overline{A_2 B_2}}{\overline{A_1 B_1}}=\dfrac{\overline{ S A_2 }}{\overline{S A_1}}$.
Mit dieser Beziehung kannst du mit den Werten $\overline{A_2 B_2}=5$, $\overline{A_1 B_1}=2$ und $\overline{ S A_1 }=1$ die fehlende Länge berechnen:
- $\overline{ S A_2 }=\frac{\overline{A_2 B_2}}{\overline{A_1 B_1}} \cdot \overline{ S A_1 }= \frac{5}{2} \cdot 1= 2,5$.
- Aus $\overline{A_2 B_2}=10$, $\overline{ S A_2 }=6$ und $\overline{ S A_1 }=3$ folgt: $\overline{A_1 B_1}=5$.
- Und mit $\overline{ S B_1 }=15$, $\overline{ S A_2 }=2$ und $\overline{ S A_1 }=5$ erhältst du $\overline{ S B_2 }=6$.
-
Beschrifte die Zeichnung.
TippsLängen zwischen zwei Punkten beschriftest du immer durch die Bezeichnung der beiden Endpunkte, über die du eine Strecke mit der jeweiligen Länge zeichnest.
Anhand der Längen kannst du erkennen, wie die Endpunkte der Länge bezeichnet werden.
LösungSo kannst du das Bild beschriften:
- Längen zwischen zwei Punkten beschriftest du immer durch die Bezeichnung der beiden Endpunkte, über die du eine Linie zeichnest.
- Anhand der Längen kannst du erkennen, wie die Endpunkte der Länge bezeichnet werden.
-
Leite die korrekten Aussagen zu Sammellinsen her.
TippsDie Mittellinie und die rote und grüne Gerade kannst du als die sich schneidenden Geraden betrachten.
Die Gegenstandsgröße $G$ könntest du auch in die Linse verschieben.
LösungFolgende Aussagen sind falsch:
„Nach dem ersten Strahlensatz gilt: $\dfrac{f}{2}=\dfrac{g}{b}$“
- Keiner der Strahlensätze gibt diese Beziehung her.
- Das kann nicht sein, da $F$ direkt auf der Mittellinie liegt. Es gilt also $F=0$, während das Verhältnis $\dfrac{B}{b}$ nicht verschwindet.
„Es gilt: $\dfrac{G}{B}=\dfrac{g}{b}$“
- Hier kannst du die Mittellinie und die grüne Gerade als die sich schneidenden Geraden betrachten. $G$ und $B$ sind die Parallelen. Mit dem zweiten Strahlensatz ergibt sich die genannte Beziehung.
- Hier betrachtest du die Mittellinie und die rote Gerade rechts von der Linse als die sich schneidenden Geraden. $G$ und $B$ sind die Parallelen (Die Gegenstandsgröße $G$ könntest du auch in die Linse verschieben.). Mit dem zweiten Strahlensatz ergibt sich die genannte Beziehung.
8.905
sofaheld-Level
6.601
vorgefertigte
Vokabeln
7.695
Lernvideos
37.343
Übungen
33.674
Arbeitsblätter
24h
Hilfe von Lehrkräften
Inhalte für alle Fächer und Klassenstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebeziehungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Quadrat
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Was Ist Eine Viertelstunde
- Prisma
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Satz Des Pythagoras
- Dreieck Grundschule
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Zahlen In Worten Schreiben
- Meter
- Orthogonalität
- Schriftlich Multiplizieren
- Brüche gleichnamig machen
- Brüche Multiplizieren
- Potenzgesetze
- Distributivgesetz
- Bruchgleichungen lösen – Übungen
- Flächeninhalt Dreieck
- Rationale Zahlen
- Volumen Berechnen
Hallo Jael Guenther,
der erste Strahlensatz beinhaltet nur Strecken, die von dem Zentrum S ausgehen, weshalb deine Gleichung nicht dem ersten Strahlensatz entspricht.
Man kann mit SA1/SA2=A1B1/A2B2 natürlich die Strecke A1B1 berechnen, allerdings ist das der zweite Strahlensatz.
Liebe Grüße aus der Redaktion!
Koennte man bei Aufgabe 3 nicht auch den ersten Strahlensatz anwenden um A1B1 auszurechen?
z.B. so: SA1/SA2=A1B1/A2B2