Strahlensätze
Tauche ein in die Welt der Geometrie und entdecke, wie du mit den Strahlensätzen spielend leicht fehlende Strecken in geometrischen Figuren berechnen kannst! Erfahre im Video, wie du ein Strahlensatzfigur aufbaust und praktische Rechenbeispiele löst. Interessiert? Schau dir das Video an und werde zum Experten in Strahlensätzen!
in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.

Grundlagen zum Thema Strahlensätze
Strahlensatz Definition
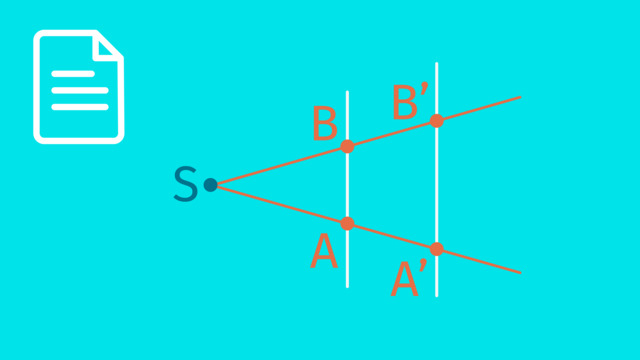
In diesem Video werden die beiden Strahlensätze verständlich erklärt. Mit Strahlensätzen kann man in einer Strahlensatzfigur aus drei vorgegebenen Strecken eine vierte Strecke berechnen. Eine Strahlensatzfigur besteht aus zwei Strahlen mit einem gemeinsamen Zentrum $S$ und zwei Parallelen, die diese Strahlen schneiden. Man bezeichnet die Schnittpunkte der beiden Parallelen mit dem einen Strahl als $A$ und $A'$, die Schnittpunkte mit dem anderen Strahl als $B$ und $B'$.
1. Strahlensatz: Definition
Im 1. Strahlensatz liegen alle Strecken auf den beiden Strahlen.
Im Bild siehst du eine Strahlensatzfigur für den 1. Strahlensatz. Die Aussage des Strahlensatzes ist eine Gleichung für Verhältnisse von Strecken. Folgende Streckenverhältnisse sind jeweils gleich:
$ \dfrac{\overline{SA}}{\overline{SA'}} = \dfrac{\overline{SB}}{\overline{SB'}} \newline {}\newline \dfrac{\overline{SA}}{\overline{AA'}} = \dfrac{\overline{SB}}{\overline{BB'}} \newline {}\newline \dfrac{\overline{SA'}}{\overline{AA'}} = \dfrac{\overline{SB'}}{\overline{BB'}} \newline $
Die Strecken auf der linken Seite jeder dieser Gleichungen gehören zu dem Strahl durch die Punkte $A$ und $A'$, die Strecken auf der rechten Seite zu dem Strahl durch die Punkte $B$ und $B'$.
2. Strahlensatz: Definition
Der 2. Strahlensatz stellt das Verhältnis der beiden Strecken auf den Parallelen durch ein Verhältnis von Strecken eines der beiden Strahlen dar. Der Strahlensatz lässt sich durch folgende Gleichungen von Streckenverhältnissen ausdrücken:
$ \dfrac{\overline{AB}}{\overline{A'B'}} = \dfrac{\overline{SA}}{\overline{SA'}} \newline {} \newline \dfrac{\overline{AB}}{\overline{A'B'}} = \dfrac{\overline{SB}}{\overline{SB'}} $
In der ersten Gleichung steht rechts ein Streckenverhältnis auf dem Strahl durch $A$ und $A'$, in der zweiten Gleichung steht das entsprechende Streckenverhältnis auf dem Strahl durch $B$ und $B'$.
Strahlensatz – Beispiel
In dem Beispiel hier im Bild sind die Strecken $\overline{SA}=20$ und $\overline{AA'} = 27$ sowie $\overline{AB} = 14$ vorgegeben. Um den 2. Strahlensatz anwenden zu können, müssen drei der vier Größen aus einer der beiden Gleichungen gegeben sein. Das ist mit den hier gegebenen Größen nicht der Fall, aber man kann die Strecken $\overline{SA}$ und $\overline{AA'}$ zu der Strecke $\overline{SA'}$ zusammensetzen:
$\overline{SA'} = \overline{SA} + \overline{AA'} = 20 + 27 = 47$
Nun kann man in die Formel
$\dfrac{\overline{AB}}{\overline{A'B'}} = \dfrac{\overline{SA}}{\overline{SA'}}$
aus dem 2. Strahlensatz die gegebenen Größen einsetzen:
$\dfrac{14}{\overline{A'B'}} = \dfrac{20}{47}$
Das Auflösen der Gleichung nach der gesuchten Strecke $\overline{A'B'}$ ergibt:
$\overline{A'B'} = 14 \cdot \dfrac{47}{20} \approx 32,9$
Strahlensatz: Spezialfall bzw. Verallgemeinerung
Man kann die beiden Strahlen auch über den Scheitelpunkt $S$ hinaus verlängern. Die parallelen Geraden können dann auf verschiedenen Seiten des Scheitelpunktes liegen. In diesem Fall gelten in beiden Strahlensätzen dieselben Gleichungen wie oben.
Strahlensätze – Ausblick
Als nächstes kannst du dein Wissen über Geometrie erweitern, indem du dich mit dem Thema Ähnlichkeit von Dreiecken beschäftigst.
Wenn du das Thema lieber direkt vertiefen und üben möchtest, schau mal beim Übungstext zu den Strahlensätzen vorbei!
Kurze Zusammenfassung zum Video Strahlensätze
In diesem Video werden die beiden Strahlensätze und ihre Begriffe verständlich erklärt. Du erfährst, welche Streckenverhältnisse in den Strahlensätzen verglichen werden. Zu jedem der Strahlensätze wird ein Zahlenbeispiel vorgerechnet.
Transkript Strahlensätze
Hast du schon einmal Schattenfiguren wie diese gesehen...oder sogar selber gemacht? Je nachdem, wie du deine Hand vor das Licht hältst, kannst du größere und kleinere Figuren zum Leben erwecken. Um zu berechnen, wie groß eine Schattenfigur auf der Leinwand erscheinen wird, können die Strahlensätze verwendet werden. Voraussetzung zur Anwendung der Strahlensätze ist, dass sich zwei Strahlen in EINEM Punkt schneiden. Ungefähr so, wie der Lichtkegel von einer Lampe. Diese beiden Strahlen werden von zwei Geraden geschnitten, die parallel zueinander sind. Hältst du deine Hand gerade vor den Lichtkegel, so ist ihr Schatten parallel zu deiner Hand. Dadurch entstehen 4 Schnittpunkte: A und A' und B und B'. So eine Figur nennt man eine Strahlensatzfigur. Sie besteht aus zwei Strahlen, die von einem gemeinsamen Punkt S – dem Scheitel – ausgehen und aus zwei Parallelen, die diese Strahlen schneiden. In einer Strahlensatzfigur kannst du die Länge einer FEHLENDEN Strecke ausrechnen, wenn du drei andere kennst. Dazu muss man nur die verschiedene Seitenverhältnisse betrachten. So ist das Verhältnis der Strecken von SA und SA' das gleiche wie das Verhältnis der Strecke von SB und SB'. Das Verhältnis von SA und AA' ist das gleiche wie das Verhältnis von SB und BB'. Und das Verhältnis von SA' und AA' mit SB' und BB' ist ebenfalls gleich. Das ist der erste Strahlensatz. Der zweite Strahlensatz gibt eine Aussage über die folgenden Seitenverhältnisse: AB geteilt durch A'B' ist gleich SA geteilt durch SA' und AB geteilt durch A'B' ist gleich SB geteilt durch SB'. Schauen wir uns dazu doch einmal ein paar Beispiele an und beginnen mit der Anwendung des ERSTEN Strahlensatzes. Du hast folgende Seitenlängen gegeben. Gesucht ist DIESE Seitenlänge. Betrachte nun die gegebenen Seiten und überlege dir, welche Gleichung du verwenden kannst. In dieser Gleichung können wir alle gegebenen Seiten und die zu berechnende Seite finden. Dazu setzen wir die gegebenen Werte zunächst ein. Achte bei SB' darauf, dass du DIESE beiden Werte zunächst addieren musst, um die Gesamtlänge der Strecke zu erhalten. Nun können wir nach SA umstellen und erhalten das Ergebnis. Diese Strecke ist ca. 21,78 lang. Schauen wir uns noch ein Beispiel zum 2. Strahlensatz an. Dieses mal haben wir diese Strecken gegeben. Betrachte nun die gegebenen Seiten und überlege dir, welche Gleichung du verwenden kannst. Du kannst DIESE Gleichung verwenden. Nun kannst du die Werte wieder einsetzen und umstellen. Hier benötigst du den Kehrwert. Diese Strecke ist also 32.9 cm lang. Fassen wir das noch einmal zusammen. Voraussetzung zur Anwendung der Strahlensätze ist, dass sich zwei Strahlen in EINEM Punkt schneiden. Diese beiden Strahlen werden von zwei Geraden geschnitten, die parallel zueinander sind. Dadurch entstehen 4 Schnittpunkte: A und A' und B und B'. So eine Figur nennt man eine Strahlensatzfigur. In einer Strahlensatzfigur kannst du die Länge einer fehlenden Strecke ausrechnen, wenn du drei andere kennst. Der erste Strahlensatz gibt eine Aussage über DIESE Verhältnisse. In dem zweiten Strahlensatz geht es um DIESE Verhältnisse. Hast du 3 Streckenlängen gegeben und willst eine Vierte herausfinden, kannst du immer gleich vorgehen: 1. Entscheide, welchen Strahlensatz du verwenden kannst. 2. Setze die gegebenen Größen in die Verhältnisgleichung ein. 3. Stelle die Gleichung um, um die gesuchte Streckenlänge herauszufinden. Jetzt wissen wir also, wie wir ganz große und ganz kleine Schattenbilder machen können. Wow! Wie bekommt man denn SO EIN Schattenbild hin? Ah, ist nur eine Mücke.
Strahlensätze Übung
-
Berechne die Länge $\overline{SA}$ mit dem 1. Strahlensatz.
TippsBerechne die Länge der Strecke $\overline{SB'}$.
Setze die Längen der Strecken in die Formel ein.
Setze in der zweiten Zeile der Rechnung die Längen der Strecken aus der ersten Zeile ein.
LösungMit dem Strahlensatz kannst du in einer Strahlensatzfigur die Länge einer Strecke aus drei anderen Strecken berechnen. In der Figur im Bild kannst du den $1.$ Strahlensatz verwenden. Um die passende Gleichung zu finden, musst du zuerst herausfinden, welche Gleichung die unbekannte Länge und die bekannten Längen enthält. Der erste Strahlensatz wird durch folgende drei Gleichungen ausgedrückt:
$ \begin{array}{rcl} \dfrac{\overline{SA}}{\overline{SA'}} &=& \dfrac{\overline{SB}}{\overline{SB'}} \\ && \\ \dfrac{\overline{SA}}{\overline{AA'}} &=& \dfrac{\overline{SB}}{\overline{BB'}} \\ && \\ \dfrac{\overline{SA'}}{\overline{AA'}} &=& \dfrac{\overline{SB'}}{\overline{BB'}} \end{array} $
Hier kommt nur die erste Gleichung infrage, denn die beiden anderen Gleichungen enthalten entweder $\overline{SA}$ gar nicht oder zusätzlich die unbekannte Strecke $\overline{AA'}$.
Du kannst hier die erste Gleichung nach der Länge der unbekannten Strecke $\overline{SA}$ umstellen. Dazu musst du noch die Länge der Strecke $\overline{SB'}$ berechnen. Diese ist die Summe der Längen der Strecken $\overline{SB}$ und $\overline{BB'}$. Es ist also:
$\overline{SB'} = \overline{SB} + \overline{BB'} = 20+25 =45$
Damit erhältst du für die Länge der Strecke $\overline{SA}$ die folgende Rechnung:
$ \begin{array}{rcl} \overline{SA} &=& \dfrac{\overline{SB}}{\overline{SB'}} \cdot \overline{SA'} \\ && \\ &=& \dfrac{20 \cdot 49}{45} \\ && \\ &=& \dfrac{980}{45} \\ && \\ &\approx& 21{,}78 \end{array} $
-
Zeige die Seiten in den Strahlensätzen.
TippsDie Strecken auf den beiden Parallelen kommen nur im $2.$ Strahlensatz vor.
In den Gleichungen des $1.$ Strahlensatzes stehen die Punkte $A$ und $B$ bzw. $A'$ und $B'$ stets auf verschiedenen Seiten.
In dieser Figur besagt der $2.$ Strahlensatz:
$\frac{14}{32,9} = \frac{20}{47}$
LösungDie beiden Strahlensätze vergleichen die Längenverhältnisse verschiedener Strecken in einer Strahlensatzfigur. Die Strecken in den Gleichungen kannst du in der Strahlensatzfigur identifizieren.
Der $1.$ Strahlensatz lässt sich durch folgende Gleichungen ausdrücken:
$ \begin{array}{rcl} \frac{\overline{SA}}{\overline{SA'}} &=& \frac{\overline{SB}}{\overline{SB'}} \\ && \\ \frac{\overline{SA}}{\overline{AA'}} &=& \frac{\overline{SB}}{\overline{BB'}} \\ && \\ \frac{\overline{SA'}}{\overline{AA'}} &=& \frac{\overline{SB'}}{\overline{BB'}} \end{array} $
Der $2.$ Strahlensatz kann analog durch folgende beiden Gleichungen ausgedrückt werden:
$ \begin{array}{rcl} \frac{\overline{AB}}{\overline{A'B'}} &=& \frac{\overline{SA}}{\overline{SA'}} \\ && \\ \frac{\overline{AB}}{\overline{A'B'}} &=& \frac{\overline{SB}}{\overline{SB'}} \\ \end{array} $
Die fehlenden Strecken in der Gleichung für den $1.$ Strahlensatz sind $\overline{SA'}$ ($1.$ Gleichung) und $\overline{BB'}$ ($2.$ Gleichung). In der dritten Gleichung fehlen noch einmal dieselben beiden. Für den $2.$ Strahlensatz sind die Strecken $\overline{SB}$ ($2.$ Gleichung) und $\overline{A'B'}$ (in beiden Gleichungen) gesucht.
-
Berechne die Länge mit einem Strahlensatz.
TippsDer $1.$ Strahlensatz vergleicht die Längenverhältnisse einander entsprechender Strecken auf den beiden Strahlen. Auf der einen Seite der Gleichung stehen Längen des einen Strahls, auf der anderen Seite entsprechende Längen des anderen Strahls.
Für die Längen der parallelen Strecken gilt z. B. die Gleichung:
$\frac{\overline{AB}}{\overline{A'B'}} = \frac{\overline{SB}}{\overline{SB'}}$
In dieser Strahlensatzfigur gilt:
$\frac{\overline{SA}}{49} = \frac{20}{45}$
LösungMithilfe der Strahlensätze kannst du die Länge einer Strecke in einer Strahlensatzfigur aus drei anderen Strecken berechnen. Die Formeln der Strahlensätze sind jeweils Gleichungen für Längenverhältnisse, die du nach der gesuchten Länge auflösen kannst. Dazu musst du zuerst eine passende Gleichung finden, in der die drei gegebenen (oder daraus abgeleitete) und die gesuchte Strecke vorkommen.
Im Bild siehst du die Strahlensatzfiguren von oben mit den jeweils fehlenden Strecken. Hier ist die Berechnung dazu:
Beispiel 1:
Gesucht ist die Länge $\overline{SB'}$, vorgegeben sind die Längen $\overline{SA}= 20$, $\overline{AA'}= 10$ und $\overline{SB}= 30$. Du kannst die Länge $\overline{SA'} = \overline{SA} + \overline{AA'} = 20+10=30$ daraus berechnen. Dann kannst du die Formel
$\frac{\overline{SA}}{\overline{SA'}} = \frac{\overline{SB}}{\overline{SB'}}$
aus dem $1.$ Strahlensatz nach $\overline{SB'}$ umstellen und erhältst:
$\overline{SB'} = \frac{\overline{SB} \cdot \overline{SA'}}{\overline{SA}} = \frac{30 \cdot 30}{20} = 45$
Beispiel 2:
Gesucht ist hier die Strecke $\overline{SA}$, vorgegeben sind die Strecken $\overline{SB}=35$, $\overline{BB'} = 7$ und $\overline{AA'}=8$. Aus dem $1.$ Strahlensatz verwendest du die Gleichung
$\frac{\overline{SA}}{\overline{AA'}} = \frac{\overline{SB}}{\overline{BB'}}$
Durch Umstellen nach $\overline{SA}$ erhältst du:
$\overline{SA}= \frac{\overline{SB} \cdot \overline{AA'}}{\overline{BB'}} = \frac{35 \cdot 8}{7} = 40$
Beispiel 3:
Vorgegeben sind hier die Strecken $\overline{SA}= 30$, $\overline{SA'}= 36$ und $\overline{AB}= 35$, gesucht ist die Strecke $\overline{A'B'}$. Die Gleichung
$\frac{\overline{AB}}{\overline{A'B'}} = \frac{\overline{SA}}{\overline{SA'}}$
aus dem $2.$ Strahlensatz kannst du nach $\overline{A'B'}$ auflösen und erhältst:
$\overline{A'B'} = \frac{35 \cdot 36}{30} = 42$
Beispiel 4:
Hier sind die Strecken $\overline{SA}= 15$, $\overline{AA'}= 5$ sowie $\overline{A'B'}= 28$ und die Strecke $\overline{AB}$ ist gesucht. Du kannst die Gleichung
$\frac{\overline{AB}}{\overline{A'B'}} = \frac{\overline{SA}}{\overline{SA'}}$
aus dem $2.$ Strahlensatz nach $\overline{AB}$ auflösen. Für die Rechnung musst du noch die Strecke $\overline{SA'} = \overline{SA} + \overline{AA'} = 15+5=20$ verwenden. Du erhältst dann:
$\overline{AB} = \frac{\overline{A'B'} \cdot \overline{SA}}{\overline{SA'}} = \frac{28 \cdot 15}{20} = 21$
Beispiel 5:
In dieser Strahlensatzfigur sind die Strecken $\overline{SB}= 19$, $\overline{SB'}= 57$ und $\overline{A'B'}= 51$ vorgegeben, die Strecke $\overline{AB}$ ist gesucht. Du kannst hier die Gleichung
$\frac{\overline{AB}}{\overline{A'B'}} = \frac{\overline{SB}}{\overline{SB'}}$
aus dem $2.$ Strahlensatz nach $\overline{AB}$ auflösen und erhältst:
$\overline{AB} = \frac{\overline{SB} \cdot \overline{A'B'}}{\overline{SB'}} = \frac{19 \cdot 51}{57} = 17$
-
Bestimme die gesuchten Längen mithilfe des Strahlensatzes.
TippsDie Strecken auf den Parallelen kommen in den Gleichungen des $1.$ Strahlensatzes nicht vor.
Der Berg ist im selben Verhältnis höher als der Kirchturm, wie er weiter entfernt ist als der Kirchturm.
LösungDie beiden Strahlensätze lassen sich in verschiedenen Situationen anwenden, in denen du die Länge einer Strecke aus drei anderen Strecken berechnen willst. Dazu müssen die Strecken bestimmte Bedingungen erfüllen:
- Sie müssen zu einer Strahlensatzfigur aus zwei Strahlen mit gemeinsamem Scheitel und zwei diese Strahlen schneidenden Parallelen gehören.
- Die Strecken müssen zueinander passen, sodass sich eine der Gleichungen aus den Strahlensätzen nach der unbekannten Strecke auflösen lässt und auf der anderen Seite nur $3$ bekannte Strecken stehen.
Es gilt:
- Die Höhe des Kirchturms in der ersten Figur entspricht der Länge der Strecke $\overline{A'B'}$.
- Die Breite des Flusses im $2.$ Beispiel entspricht der Länge der Strecke $\overline{AB}$.
Der Strahlensatz macht eine Aussage über die Längenverhältnisse, daher kannst du mit dem Strahlensatz auch Folgerungen über Längenverhältnisse ziehen: Der Betrachter steht am Scheitelpunkt $S$ der Strahlensatzfigur. Die vom Betrachter ausgehende Horizontale enthält die Punkte $A$ beim Fußpunkt des Kirchturms und $A'$ am Fuß des Bergs. Die Blicklinie verläuft vom Betrachter über die Kirchturmspitze $B$ zum Gipfel $B'$ des Bergs. Ist der Abstand zwischen Betrachter und Kirchturm dreimal so groß wie der zwischen Kirchturm und Berg, so ist:
- $\frac{SA}{AA'} = 3$ und $\frac{SA'}{AA'} = 4$ und $\frac{SA'}{SA} = \frac{4}{3}$
- $\frac{\overline{A'B'}}{\overline{AB}} = \frac{\overline{SA'}}{\overline{SA}} = \frac{4}{3}$
Ist $\overline{AA'}=15~\text{km}$ und $\overline{SA} = 45~\text{km}$, so ist die Höhe des Bergs das Produkt der Höhe des Kirchturms mit:
- $\frac{\overline{SA'}}{\overline{SA}} = \frac{45+15}{45}= { \frac{60}{45}}$.
$\overline{A'B'} = \frac{\overline{AB} \cdot \overline{SA'}}{\overline{SA}} =18~ \text m \cdot \frac{60}{45} = 24~\text m$
Beispiel 2:
Bei der Anwendung des Strahlensatzes müssen die beiden Parallelen nicht auf derselben Seite des Scheitels der Strahlen liegen. Die Figur im Bild ist eine Strahlensatzfigur, denn die beiden Strahlen durch die Punkte $A$ und $A'$ bzw. $B$ und $B'$ schneiden sich im Scheitelpunkt $S$ und die Strecken $\overline{AB}$ und $\overline{A'B'}$ sind parallel zueinander. Denn sie sind beide senkrecht zu der Strecke $\overline{AA'}$.
Mit dem ${2.}$ Strahlensatz kannst du die Breite $\overline{AB}$ des Flusses berechnen. Ist $\overline{SA} = 24~\text m$ und $\overline{SA'}=9~\text m$ und $\overline{A'B'}=3~\text{m}$, so erhältst du die Breite des Flusses aus dem $2.$ Strahlensatz:
- $\overline{AB} = \frac{\overline{A'B'} \cdot \overline{SA}}{\overline{SA'}}= \frac{3~\text m \cdot 24~\text m}{9~\text m} = 8~\text m$
-
Gib die Eigenschaften der Strahlensätze und Strahlensatzfiguren wieder.
TippsEinen Strahl nennt man auch Halbgerade.
Jede Gleichung aus den Strahlensätzen kannst du nach einer Strecke auflösen und deren Länge aus den anderen Längen berechnen.
Dies ist keine Strahlensatzfigur.
LösungFolgende Sätze sind richtig:
- „In jeder Strahlensatzfigur kommen zwei Strahlen mit gemeinsamem Scheitel und zwei diese Strahlen schneidende Parallelen vor.“ Das ist die Definition der Strahlensatzfigur. Du siehst eine solche Strahlensatzfigur hier im Bild. Die beiden Strahlen gehen von $S$ aus, die beiden Parallelen laufen durch die Punkte $A$ und $B$ bzw. $A'$ und $B'$.
- „Die Strahlensätze vergleichen die Längenverhältnisse verschiedener Strecken in einer Strahlensatzfigur.“ Die Gleichungen der Strahlensätze sind Aussagen über die Längenverhältnisse der Strecken in der Strahlensatzfigur. Im Bild siehst du eine Gleichung aus dem ersten Strahlensatz. Sie vergleicht das Verhältnis der Länge $\overline{SA}$ zur Länge $\overline{SA'}$ mit dem Verhältnis der Länge $\overline{SB}$ zur Länge $\overline{SB'}$.
- „Ein Strahl hat einen Anfangs- und Endpunkt.“ Ein Strahl ist dasselbe wie eine Halbgerade. Diese hat einen Anfangspunkt, aber keinen Endpunkt.
- „Der Scheitel einer Strahlensatzfigur ist ein Punkt auf einer der Parallelen.“ Der Scheitel der Strahlensatzfigur ist der Punkt $S$ im Bild, in dem sich die beiden Strahlen schneiden. Die beiden Parallelen verlaufen nicht durch den Scheitelpunkt $S$.
- „Mit den Strahlensätzen kannst du die Länge einer Strecke aus zwei anderen Strecken berechnen.“ Um eine Strecke in einer Strahlensatzfigur mithilfe der Strahlensätze zu berechnen, brauchst du drei Strecken. Denn jede Gleichung enthält vier Strecken. Wenn du die Gleichung nach einer Strecke auflöst, bleiben drei Strecken auf der anderen Seite der Gleichung, die du kennen musst, um die unbekannte Strecke auszurechnen. Löst du zum Beispiel die Formel im Bild nach einer Länge auf, so stehen auf der anderen Seite der Gleichung drei Längen. Diese drei Längen musst du kennen, um die vierte Länge berechnen zu können.
-
Prüfe die Anwendungen der Strahlensätze.
TippsMit dem $2.$ Strahlensatz bestimmte Thales von Milet die Höhe der Cheopspyramide aus der Länge des Stabs sowie seiner Abstände zum Stab und zur Pyramide.
LösungFolgende Aussagen sind richtig:
Schatten des Daumens:
Beim Peilen über den Daumen erhältst du die Strahlensatzfigur hier im Bild. Der Scheitelpunkt $S$ ist dein Daumen, die Strahlen sind die Blicklinien deiner beiden Augen. Dein Augenabstand ist die Strecke $\overline{AB}$, der Abstand zwischen den beiden scheinbaren Positionen deines Daumens ist $\overline{A'B'}$. Du kannst mit dem $2.$ Strahlensatz die Länge $\overline{A'B'}$ aus deiner Armlänge $\overline{SA}$, deinem Augenabstand $\overline{AB}$ und dem Abstand $\overline{SA'}$ zur Leinwand berechnen.
Wenn du noch genauer rechnen willst, kannst du einen weiteren Strahl von der Mitte $C$ zwischen deinen beiden Augen zum Mittelpunkt $C'$ der Strecke $A'B'$ konstruieren. Der Abstand zur Leinwand ist dann die Strecke $\overline{CC'}$, die du mit dem $1.$ Strahlensatz aus den gegebenen Strecken berechnen kannst. Für praktische Rechnungen macht das aber kaum einen Unterschied, weil die Strecken $\overline{SC'}$ und $\overline{SA'}$ annähernd gleich lang sind.
Felsen:
Die Strahlensatzfigur besteht aus den Blicklinien, die von deinem Auge über deine Fingerkuppe zur Spitze des Felsens sowie von deinem Auge über deine Daumenwurzel zum Fußpunkt des Felsens verlaufen. Die Höhe des Felsens entspricht der Strecke $\overline{A'B'}$ in der Strahlensatzfigur, die Länge deines Daumens der Strecke $\overline{AB}$. Deine Armlänge entspricht der Strecke $\overline{SA}$, und die gesuchte Entfernung zu dem Felsen ist die Strecke ${SA'}$.
Folgende Aussagen sind falsch:
Sonne:
In einer Strahlensatzfigur, mit der du die Sonne anpeilst, entspricht der Durchmesser der Sonne der Strecke $\overline{A'B'}$. Du kannst diese Strecke nur berechnen, wenn du einen der Abstände $\overline{SA'}$, $\overline{AA'}$, $\overline{SB'}$ oder $\overline{BB'}$ kennst. Du kommst also nicht allein mit den irdischen Größen $\overline{SA}$, $\overline{SB}$ und $\overline{AB}$ aus. Damit ergibt sich: Um den Durchmesser der Sonne zu bestimmen, benötigst du die Größe ihrer Entfernung. Um die Entfernung zur Sonne zu bestimmen, benötigst du die Größe ihres Durchmessers.
Mond:
Verdeckst du den Mond mit einer Kirsche, so konstruierst du eine Strahlensatzfigur. Der Durchmesser der Kirsche entspricht der Strecke $\overline{AB}$, der Durchmesser des Mondes der Strecke $\overline{A'B'}$. Verdoppelst du die Entfernung des Mondes, so ändert sich nicht die Größe des Mondes, d. h., du kannst gar nicht dieselbe Strahlensatzfigur verwenden. Die Strahlen der neuen Strahlensatzfigur liegen in einem kleineren Winkel zueinander, sodass dann auch der weiter entfernte Mond kleiner erscheint. Ganz so, wie es sein soll.
9.777
sofaheld-Level
6.600
vorgefertigte
Vokabeln
8.289
Lernvideos
38.614
Übungen
33.652
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Klassenstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung




 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?
















Vielen Dank für die Erklärung
HAB DA NE FRAGE WAS IST DIE QUADRATWURZEL VOM STRAHLENZATZ
Wieso macht man bei den 2. Strahlensatz Anwendungsaufgabe den Kehrbruch. Also Sie haben dass ja auch nicht bei 1. Strahlensatz gemacht
Frage: Wieso macht man den Kehrburch
"Warum brauche ich das?" ist eine interessante Frage in Mathematik. Eine interessante Anwendung ist die Bestimmung der Höhe eines Baumes o.ä. Man kann also mit dem Strahlensatz einfach die Höhe von großen Objekten bestimmen. Im Genrellen wird durch die Anwendung von den Strahlensätzen das abstrakte Denken geübt, in Kombination mit Anwendungen aus der Realität, wie Höhenberechnungen. D.h. man lernt Streckenverhätnise zu berechnen und sich diese Abstrakt vorzustellen.
Lol same