Satz des Pythagoras
Die Summe der beiden Kathetenquadrate ist gleich dem Hypotenusenquadrat – Der Satz des Pythagoras gilt an rechtwinkligen Dreiecken und hilft dir bei der Berechnung einer fehlenden Seitenlänge.
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
Der Satz des Pythagoras
Der Satz des Pythagoras gilt in rechtwinkligen Dreiecken, also Dreiecken mit einem Winkel von $90^\circ$.
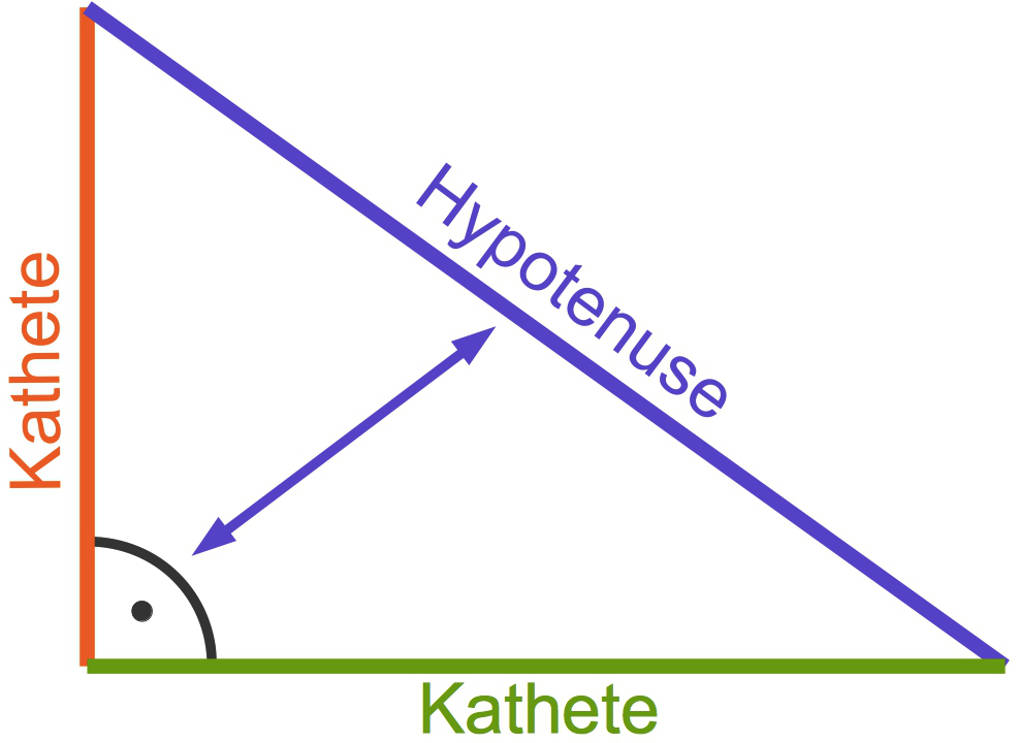
Den rechten Winkel von $90^\circ$ erkennst du an dem Punkt. Gegenüber von dem rechten Winkel befindet sich die längste Seite des rechtwinkligen Dreiecks, die Hypotenuse. Die beiden übrigen Seiten liegen an dem rechten Winkel an. Dies sind die Katheten.
Der Satz des Pythagoras ist sehr hilfreich bei der Berechnung einer unbekannten Seitenlänge in einem rechtwinkligen Dreieck, denn er besagt: Wenn du die beiden Kathetenlängen quadrierst und die Quadrate addierst, so erhältst du das Quadrat der Hypotenusenlänge.

Wie du hier siehst, sind die beiden Katheten die Seiten $a$ und $b$ und die Hypotenuse die Seite $c$. Der Flächeninhalt von $a^2$ plus der Flächeninhalt von $b^2$ ist genau so groß wie der Flächeninhalt von $c^2$. Das gilt für alle rechtwinkligen Dreiecke und wird mathematisch so ausgedrückt:
$a^2+b^2=c^2$ .
Indem du zwei bekannte Seitenlängen einsetzt und die Formel umstellst und auflöst, kannst du immer die eine unbekannte Seitenlänge ausrechnen.
Beweis des Satzes von Pythagoras
Der Satz des Pythagoras ist nach Pythagoras von Samos benannt, der um 550 v. Chr. gelebt hat. Er hat angeblich als Erster den Satz mathematisch bewiesen.
Einen der Beweise wollen wir dir hier auch zeigen:
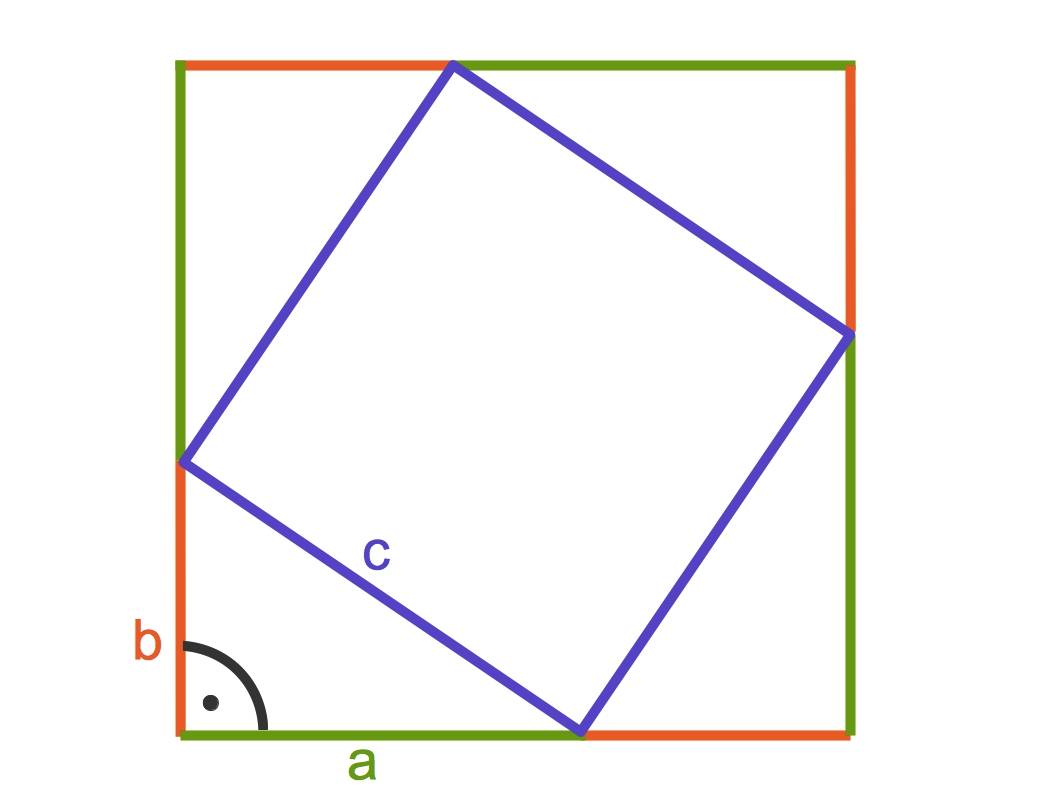
Das große Quadrat hat die Seitenlänge $a+b$. Es kann in
- ein kleineres, blaues Quadrat mit der Seitenlänge $c$, und
- vier deckungsgleiche, rechtwinklige Dreiecke, jeweils mit den Katheten $a$ und $b$ sowie der Hypotenuse $c$,
aufgeteilt werden.
Der Flächeninhalt des großen Quadrates beträgt:
$(a+b)^{2}=a^{2}+2ab+b^{2}$.
Hier wird die 1. binomische Formel verwendet.
Der Flächeninhalt des kleineren, blauen Quadrates beträgt $c^2$.
Jedes der vier Dreiecke hat den Flächeninhalt $ab:2$.
Damit gilt also:
$\begin{array}{rrrcll} a^2&+2ab&+b^2&=&c^2+4\cdot (\frac{ab}{2}) &~\\ a^2&+2ab&+b^2&=&c^2+2ab & \vert -2ab\\ a^2&+&b^2&=&c^2&~\\ \end{array}$
Da der Satz des Pythagoras für jedes rechtwinklige Dreieck in gleicher Weise bewiesen werden kann, gilt er im Umkehrschluss auch für jedes rechtwinklige Dreieck.
Anwendung des Satzes von Pythagoras
Du kannst auch den Abstand von Punkten im Koordinatensystem mit dem Satz des Pythagoras berechnen.
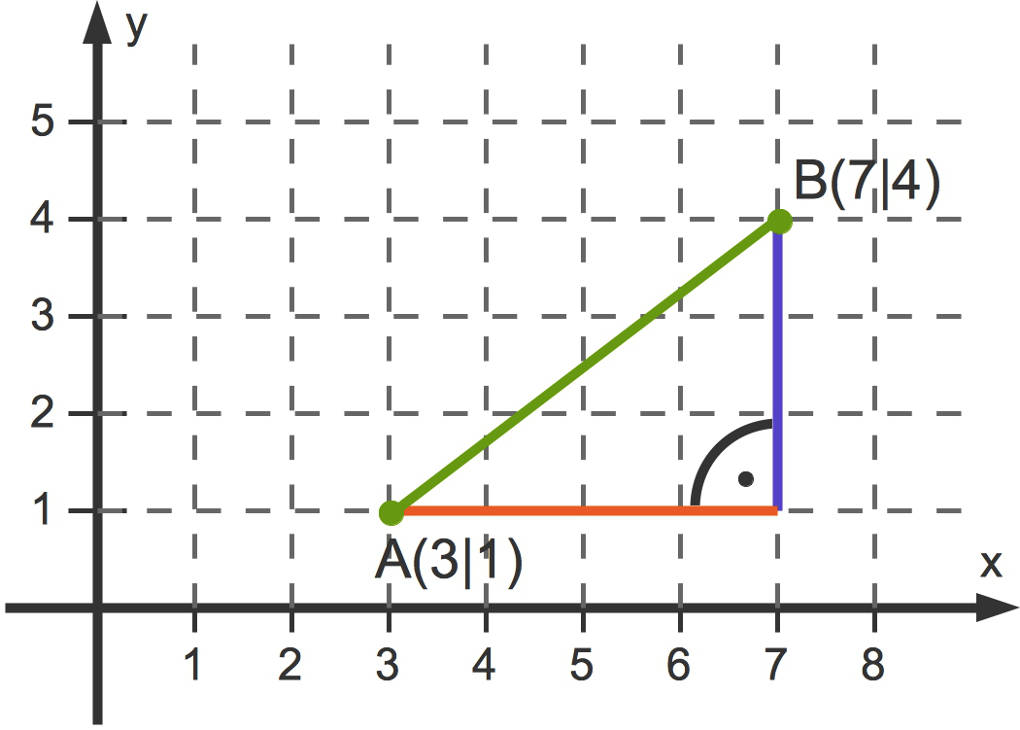
Um den Abstand zwischen den Punkten $\text{A}$ und $\text{B}$ auszurechnen (grüne Strecke), gehst du folgendermaßen vor:
- Die Differenz der x-Koordinaten der beiden Punkte $A$ und $B$ sowie die der y-Koordinaten dieser Punkte sind die Kathetenlängen in dem rechtwinkligen Dreieck.
Der Abstand $d$ der beiden Punkte zueinander ist die Länge der Hypotenuse.
So ergibt sich $(7-3)^2+(4-1)^2=d^2$
- Nun kannst du die Differenzen berechnen und quadrieren: $16+9=d^2$ oder $25=d^2$.
- Durch Ziehen der Wurzel erhältst du $d=5$ den gesuchten Abstand.
Der Satz des Pythagoras findet auch häufig Anwendung in Alltagsproblemen. Schau dir dafür das folgende Beispiel an: Paul stellt eine $6~m$ lange Leiter an einer senkrechten Hauswand im Abstand von $3~m$ auf. Wie hoch steht die Leiter an der Wand?
Fertige eine Skizze an, in der du diesen Sachverhalt festhältst. Darin kannst du erkennen, dass die Längen der Hypotenuse sowie einer Katheten bereits bekannt sind. Unbekannt ist die Länge einer Kathete, der Höhe $h$. Wenn du die bekannten Größen in den Satz des Pythagoras einsetzt, erhältst du
$(3~m)^2+h^2=(6~m)^2$.
Nun kannst du die Quadrate ausrechnen und $9~m^2$ subtrahieren und erhältst
$h^2=27~m^2$.
Zuletzt ziehst du die Wurzel und erhältst für die Höhe $h=5,2~m$.
Alle Videos und Lerntexte zum Thema
Videos und Lerntexte zum Thema
Satz des Pythagoras (7 Videos, 1 Lerntext)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Satz des Pythagoras (7 Arbeitsblätter)
-
 Der Satz des Pythagoras
PDF anzeigen
Der Satz des Pythagoras
PDF anzeigen -
 Satz des Pythagoras – Kathete gesucht
PDF anzeigen
Satz des Pythagoras – Kathete gesucht
PDF anzeigen -
 Satz des Pythagoras – Beweis
PDF anzeigen
Satz des Pythagoras – Beweis
PDF anzeigen -
 Abstand zweier Punkte – Herleitung (Satz des Pythagoras)
PDF anzeigen
Abstand zweier Punkte – Herleitung (Satz des Pythagoras)
PDF anzeigen -
 Abstand zweier Punkte berechnen
PDF anzeigen
Abstand zweier Punkte berechnen
PDF anzeigen -
 Diagonale berechnen mit dem Satz des Pythagoras
PDF anzeigen
Diagonale berechnen mit dem Satz des Pythagoras
PDF anzeigen -
 Möndchen des Hippokrates
PDF anzeigen
Möndchen des Hippokrates
PDF anzeigen
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung



















