Quadratische Ungleichungen
Du kennst bereits quadratische Gleichungen und weißt, dass du diese mit der p-q-Formel lösen kannst. Diese Formel benötigst du auch bei quadratischen Ungleichungen.
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Was ist eine quadratische Ungleichung?
- Einführung Ungleichung
- Was sind Äquivalenzumformungen?
- Quadratische Ungleichungen
Was ist eine quadratische Ungleichung?
Einführung Ungleichung
Eine Ungleichungen behandelst du fast genauso wie Gleichungen. Das Ist-Gleich-Zeichen wird ersetzt durch ein Ungleichheitszeichen (auch Vergleichszeichen genannt).
Eine lineare Ungleichung ist eine Ungleichung ersten Grades und hat zum Beispiel die Form $mx+b\le 0$. Das Vergleichszeichen kann auch $<$ oder $\ge$ oder $>$ sein. Du löst eine Ungleichung ähnlich wie eine Gleichung. Du wendest Äquivalenzumformungen an.
Was sind Äquivalenzumformungen?
Unter einer Äquivalenzumformung verstehst du Umformungen, die den Wahrheitsgehalt einer Gleichung oder Ungleichung nicht verändern.
Das Wort „Äquivalenzumformung“ kommt aus dem Lateinischen „aequus“ für „gleich“ und „valere“ für „Wert sein“.
Äquivalenzumformungen sind die Termumformungen
- auf einer oder beiden Seiten einer Gleichung.
- wie die Addition oder Subtraktion eines Terms auf beiden Seiten der Gleichung oder Ungleichung.
- wie die Multiplikation oder Division mit einem Term ungleich $0$ auf beiden Seiten der Gleichung oder Ungleichung.
Beachte bei der Multiplikation und der Division mit einer Zahl (oder auch einem Term) bei Ungleichungen:
- Wenn die Zahl (oder der Term) positiv ist, ändert sich das Relationszeichen nicht.
- Ist die Zahl (oder der Term) allerdings negativ, musst du das Relationszeichen umdrehen.
Das kannst du an dem folgenden Beispiel einer linearen Ungleichung sehen:
$\begin{array}{crclll} &2x+3&<&5&|&\cdot (-2)\\ \Leftrightarrow&(-2)\cdot (2x+3)&>&(-2)\cdot 5 \end{array}$
Quadratische Ungleichungen
Eine quadratische Ungleichung hat die allgemeine Form $ax^2+bx+c\le 0$. Das Vergleichszeichen kann auch $<$ oder $\ge$ oder $>$ sein.
Lösen einer allgemeinen quadratische Ungleichung.
Wie gehst du beim Lösen einer quadratischen vor? Du führst die folgenden vier Schritte durch:
Normalform: Dividiere die gesamte Ungleichung $ax^2+bx+c\le 0$ durch $a$, den Faktor vor dem $x^2$. Ist $a$ positiv hast du eine Ungleichung der Form $x^2+\frac{b}{a}x+\frac{c}{a}\le 0$. Zur einfacheren Darstellung wurden die Variablen $p$ und $q$ eingeführt, wobei gilt $p=\frac{b}{a}$ und $q=\frac{c}{a}$. So ergibt sich für die obige Ungleichung mit positiven $a$ die Ungleichung $x^2+px+q\le 0$. Ist $a$ negativ muss das Vergleichszeichen umgedreht werden $x^2+px+q\ge 0$. Eine solche Ungleichung heißt in Normalform.
Löse Gleichung in Normalform: Löse die Gleichung $x^2+px+q=0$ zum Beispiel mit Hilfe der p-q-Formel. Die Lösungen seien $x_1$ sowie $x_2$.
Faktorisierung: Faktorisiere die linke Seite der Ungleichung. So erhältst du $(x-x_1)\cdot (x-x_2)\le 0$.
Faktorbestimmung: Betrachte die beiden Faktoren. Das Produkt zweier Faktoren ist kleiner oder gleich $0$, wenn einer der beiden Faktoren größer oder gleich $0$ ist und der andere kleiner oder gleich $0$.
Es gibt vier Fälle bei der Ungleichung.
Der vierte Schritt führt je nach Relationszeichen zu $x^2+px+q\le 0$ oder die Ungleichung mit $<$ oder $\ge$ oder $>$ Relationszeichen. Im Folgenden siehst du vier verschiedene Fälle. Dabei werden die Ungleichungen mit den Relationszeichen $<$ sowie $>$ betrachtet.
Kleiner als Relation $(x-x_1)\cdot (x-x_2)<0$
- Erster Fall: Entweder ist $x-x_1<0$ und $x-x_2>0$
- Zweiter Fall: oder $x-x_1>0$ und $x-x_2<0$
- Dies gilt übrigens ebenso für die Kleiner oder gleich Relation.
Größer als Relation $(x-x_1)\cdot (x-x_2)>0$
- Dritter Fall: Entweder ist $x-x_1>0$ und $x-x_2>0$
- Vierter Fall: oder $x-x_1<0$ und $x-x_2<0$
- Dies gilt übrigens ebenso für die Größer oder gleich Relation.
Du kannst jetzt das Lösen einer quadratischen Ungleichung an zwei Beispielen üben.
Anwendungsbeispiel zur Lösung quadratischen Ungleichungen
1. Beispiel: Quadratischen Ungleichung in Normalform
Du sollst die quadratische Ungleichung $x^2+4x-5<0$ in Normalform lösen.
Schritt 1: Bringe die Ungleichung in Normalform. Den ersten Schritt des Vorgehens zur Lösung einer quadratischen Ungleichung musst du hier nicht durchführen. Die quadratische Ungleichung liegt ja bereits in Normalform vor.
Schritt 2: Löse die Gleichung. Zur Lösung der Gleichung $x^2+4x-5=0$ kann die p-q-Formel angewendet werden. Hier ist $p=4$ und $q=-5$. So erhältst du
$\begin{array}{rcl} x_{1,2}&=&-\frac42\pm\sqrt{\left(\frac42\right)^2-(-5)}\\ &=&-2\pm\sqrt{4+5}\\ &=&-2\pm\sqrt{9}\\ x_1&=&-2+3=1\\ x_2&=&-2-3=-5 \end{array}$
Schritt 3: Faktorisiere die linke Seite der Ungleichung. Du schreibst nun $x^2+4x-5$ als Produkt $(x-1)\cdot (x+5)$ und erhältst somit die Ungleichung $(x-1)\cdot (x+5)<0$.
Schritt 4: Löse die faktorisierte Ungleichung. Beachte, dass ein Produkt zweier Faktoren ist negativ, wenn die beiden Faktoren verschiedene Vorzeichen haben. Das bedeutet: Wenn der eine Faktor negativ ist, muss der andere positiv sein, und umgekehrt. So erhältst du die folgenden beiden Fälle:
- $x-1>0$. Dann wäre $x>1$ und $x+5<0$ oder äquivalent dazu $x<-5$. Es gibt kein $x$, das gleichzeitig größer als $1$ und kleiner als $-5$ sein kann.
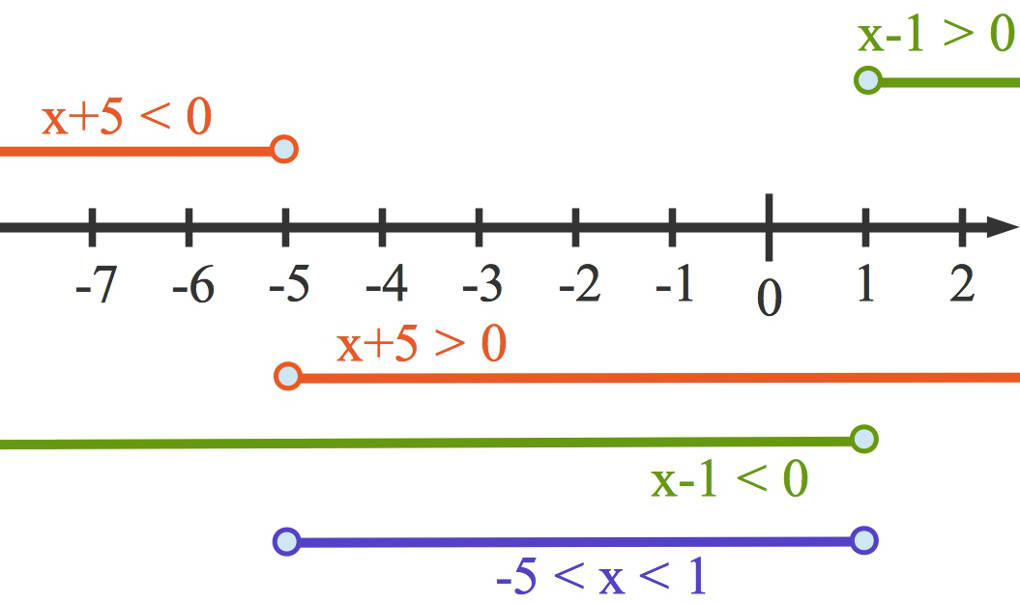
- $x-1<0$. Dann wäre $x<1$ und $x+5>0$ oder äquivalent dazu $x>-5$. Damit muss $-5<x<1$ sein.="" nun="" kannst="" du="" die="" lösungsmenge="" der="" quadratischen="" ungleichung="" angeben="" $\mathbb{l}="\{x\in\mathbb{R}~|~-5<x<1\}$." dir="" dies="" anschaulich="" an="" einem="" zahlenstrahl="" klarmachen:=""
 " *="" da="" $<$-="" oder="" $="">$-Relation betrachtet wird, müssen jeweils $-5$ und $1$ ausgeschlossen werden. Dies erkennst du an dem leeren Kreis.
" *="" da="" $<$-="" oder="" $="">$-Relation betrachtet wird, müssen jeweils $-5$ und $1$ ausgeschlossen werden. Dies erkennst du an dem leeren Kreis. - Oberhalb des Zahlenstrahls siehst du den oberen der beiden Fälle. Es gibt zu diesem Fall keine Lösungen.
- Unterhalb des Zahlenstrahls siehst du den unteren Fall sowie (blau) die Lösungsmenge.
2.Beispiel: Lösen einer allgemeinen quadratische Ungleichung.
Löse die quadratische Ungleichung: $-\frac12x^2+3x-4<0$
Multipliziere mit $-2$. Beachte, dass du das Relationszeichen umdrehen musst: $x^2-6x+8>0$ Diese Ungleichung ist in Normalform.
Bestimme die Lösungen der Gleichung $x^2-6x+8=0$. Diese erhältst du mit Hilfe der p-q-Formel: $x_1=2$ sowie $x_2=4$.
Faktorisiere die Ungleichung $(x-2)\cdot (x-4)>0$.
- Löse die Ungleichung: Entweder ist $x-2>0~\Leftrightarrow~x>2$ und $x-4>0~\Leftrightarrow~x>4$, also $x>4$. Für den zweiten Fall gilt dann $x-2<0~\Leftrightarrow~x<2$ und $x-4<0~\Leftrightarrow~x<4$, also auch $x<2$.
Auch hier kannst du dir die Lösungsmenge mit Hilfe eines Zahlenstrahls klarmachen. Den ersten der beiden Fälle siehst du wieder oberhalb und den zweiten unterhalb des Zahlenstrahls:
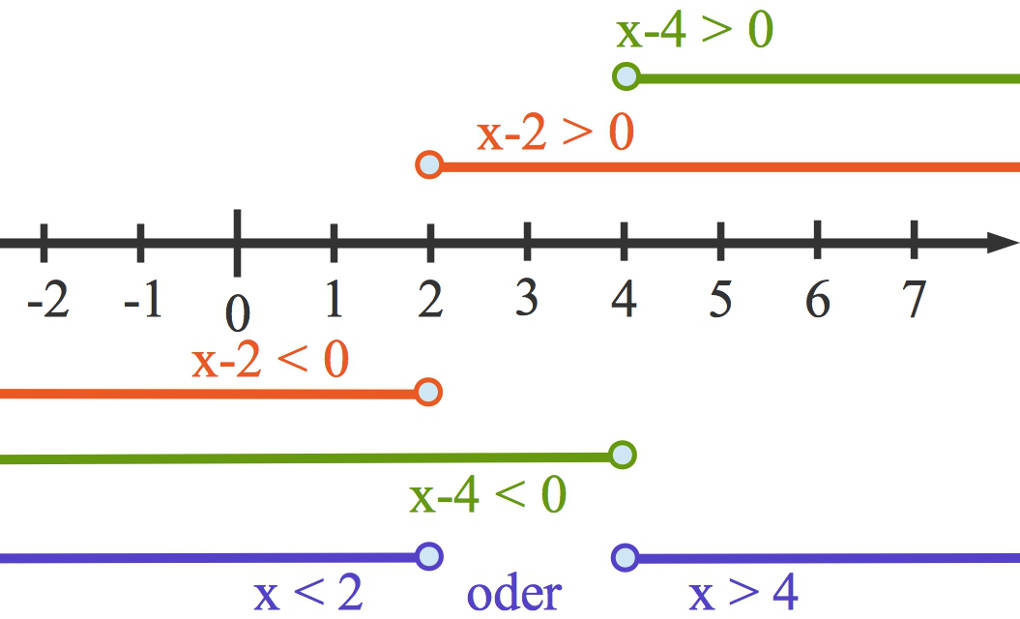
Es ist also $\mathbb{L}=\{x\in\mathbb{R}~|~x<2~\text{oder}~x>4\}$.</x<1$>
Alle Videos zum Thema
Videos zum Thema
Quadratische Ungleichungen (3 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Quadratische Ungleichungen (3 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung


 " *="" da="" $<$-="" oder="" $="">$-Relation betrachtet wird, müssen jeweils $-5$ und $1$ ausgeschlossen werden. Dies erkennst du an dem leeren Kreis.
" *="" da="" $<$-="" oder="" $="">$-Relation betrachtet wird, müssen jeweils $-5$ und $1$ ausgeschlossen werden. Dies erkennst du an dem leeren Kreis.


 Quadratische Ungleichungen rechnerisch lösen
Quadratische Ungleichungen rechnerisch lösen
 Quadratische Ungleichungen graphisch lösen
Quadratische Ungleichungen graphisch lösen
 Lösungsmengen quadratischer Ungleichungen
Lösungsmengen quadratischer Ungleichungen









