Änderungsrate, Differenzenquotient und Differentialquotient
Was ist die Änderungsrate und welche Rolle spielt sie für Funktionen und Ableitungen? Hier lernst du mehr über die mittlere und lokale Änderungsrate sowie den Differenzquotienten.
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Wofür wird die mittlere und lokale Änderungsrate benötigt?
- Die mittlere Änderungsrate
- Die lokale Änderungsrate
- Beispiel zu der lokalen und mittleren Änderungsrate
- Mittleres Wachstum
- Lokales Wachstum
Wofür wird die mittlere und lokale Änderungsrate benötigt?
Ein sehr zentraler Begriff in der Mathematik bei Funktionen ist jener der Ableitung. Um diesen Begriff zu verstehen oder um ihn herzuleiten, werden
- die mittlere Änderungsrate sowie
- die lokale Änderungsrate
betrachtet.
Kurz: Die Ableitung ist die Steigung einer Tangente.
Die mittlere Änderungsrate
Die mittlere Änderungsrate ist die Steigung einer Sekante. Was bedeutet das?
Bei einer linearen Funktion $f(x)=mx+b$ ist die Steigung bekannt. Diese ist $m$, der Faktor vor der Variablen. Der Graph einer linearen Funkion ist eine Gerade. Die Steigung einer Geraden, wenn die zugehörige Funktionsgleichung nicht gegeben ist, kann mit Hilfe eines Steigungsdreiecks bestimmt werden. Dies ist hier zu sehen.
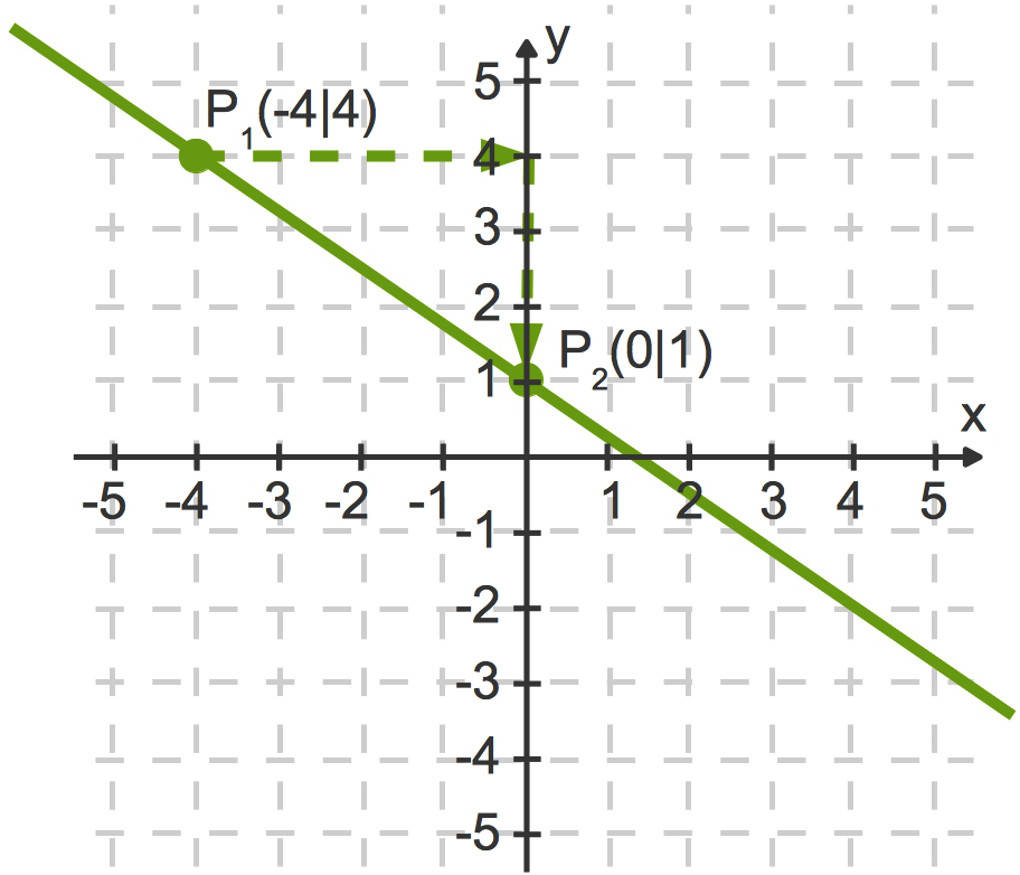
In dem Steigungsdreieck ist die Steigung gegeben als die Differenz der y-Koordinaten der beiden Punkte $P_1$ und $P_2$ dividiert durch die Differenz der entsprechenden x-Koordinaten:
$m=\frac{1-4}{0-(-4)}=\frac{-3}4=-\frac34$
Nur: Wie kann die Steigung berechnet werden, wenn der Graph der Funktion keine Gerade ist?
Hier ist eine Parabel zu sehen, der Graph der Funktion $f(x)=x^2-2$.
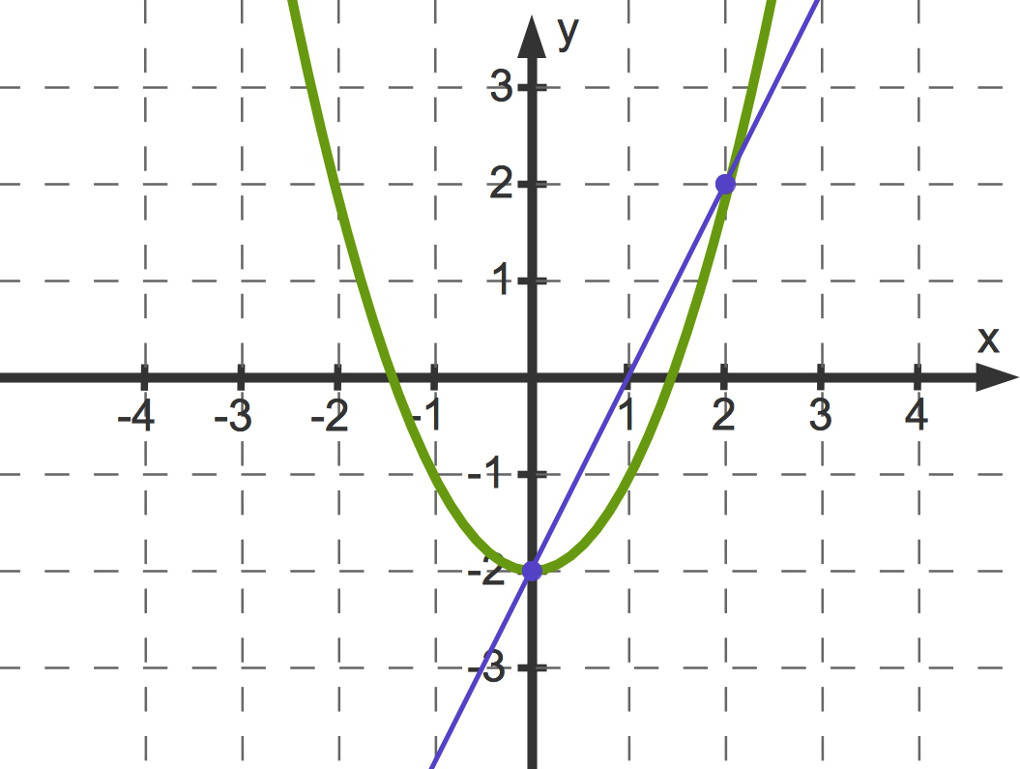
Wenn man zwei Punkte betrachtet, zum Beispiel $P_1(0|-2)$ sowie $P_2(2|2)$, so verläuft durch diese beiden Punkte eine Gerade. Diese Gerade ist eine Sekante, da sie die Parabel in zwei Punkten schneidet.
Die Steigung dieser Geraden kann wieder mit einem Steigungsdreieck bestimmt werden. Es ist
$m=\frac{2-(-2)}{2-0}=\frac42=2$
Wenn nun zwei allgemeine Punkte $P_1(x_1|y_1)$ sowie $P_2(x_2|y_2)$ gegeben sind, ist die Steigung durch die folgende Formel gegeben
$m=\frac{y_2-y_1}{x_2-x_1}$
Da die y-Koordinate eines Punktes auf einem Funktionsgraphen der Funktionswert $y=f(x)$ ist, gilt
$m=\frac{f(x_2)-f(x_1)}{x_2-x_1}$
Dies ist die Steigung der Sekante durch die Punkte $P_1(x_1|y_1)$ sowie $P_2(x_2|y_2)$. Sie wird berechnet als Quotient der Differenz der Funktionswerte und der entsprechenden Differenz der Argumente. Dieser Quotient wird deshalb als Differenzenquotient bezeichnet.
Der Differenzenquotient gibt also die Steigung einer Sekante an. Diese wird als die mittlere Änderungsrate auf dem Intervall $[x_1;x_2]$ bezeichnet.
Die lokale Änderungsrate
Die lokale Änderungsrate ergibt sich als Grenzwert der mittleren Änderungsrate und wird mit $f'(x_0)$ bezeichnet.
$f'(x_0)=\lim\limits_{x\to x_0}\frac{f(x)-f(x_0)}{x-x_0}$
Der Grenzwert der Differenzenquotienten wird als Differentialquotient bezeichnet.
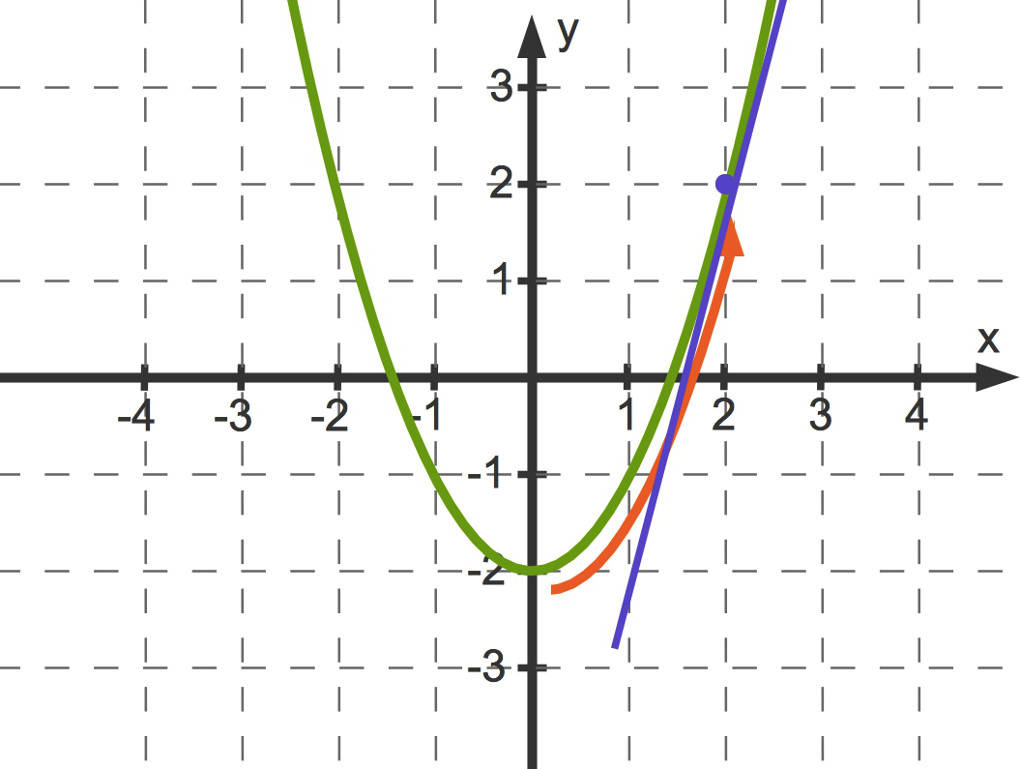
Anschaulich bedeutet dies, ausgehend von dem obigen Beispiel, dass einer der beiden Punkte fest ist, hier $P_2(2|2)$, und der andere Punkt entlang dem Funktionsgraphen zu $P_2$ „wandert“. Die so erhaltenen Sekanten nähern sich der Tangente an den Graphen der Funktion in dem Punkt $P_2$ an.
Die lokale Änderungsrate ist die Steigung dieser Tangente.
Beispiel zu der lokalen und mittleren Änderungsrate
Das Wachstum eines Baumes sei beschrieben durch $h(x)=6+\sqrt x$. Dabei ist die Höhe $h(x)$ in Metern gegeben und $x$ in Wochen.

Mittleres Wachstum
Wie sehr wächst der Baum im Zeitraum $[0;4]$. Hier ist nach der mittleren Änderungsrate gefragt. Oft wird diese, in anderen Beispielen, als Durchschnittsgeschwindigkeit, durchschnittliches Wachstum, ... bezeichnet. Erkennbar ist die mittlere Änderungsrate daran, dass ein Intervall, hier ein Zeitraum, vorgegeben wird. Mithilfe der Definition der mittleren Änderungsrate ist
$m=\frac{h(4)-h(0)}{4-0}=\frac{6+\sqrt 4-(6+\sqrt 0)}{4}=\frac{8-6}{4}=\frac24=0,5$
Der Baum wächst in den ersten vier Wochen durchschnittlich $0,5~m$ pro Woche.
Lokales Wachstum
Wie sehr wächst der Baum zum Zeitpunkt $x_0=4$? Diesmal ist nach der lokalen Änderungsrate gefragt. Diese ist wie folgt definiert:
$h'(4)=\lim\limits_{x\to 4}\frac{h(x)-h(4)}{x-4}=\lim\limits_{x\to 4}\frac{6+\sqrt x-8}{x-4}=\lim\limits_{x\to 4}\frac{\sqrt x-2}{x-4}$
Der Bruch wird mit $\sqrt x+2$ erweitert und mit Hilfe der 3. binomischen Formel umgeformt
$h'(4)=\lim\limits_{x\to 4}\frac{(\sqrt x-2)(\sqrt x+2)}{(x-4)(\sqrt x+2)}=\lim\limits_{x\to 4}\frac{x-4}{(x-4)(\sqrt x+2)}=\lim\limits_{x\to 4}\frac{1}{\sqrt x+2}$
Nun kann $x=4$ eingesetzt werden. Dies führt zu der lokalen Änderungsrate
$h'(4)=\frac{1}{\sqrt4+2}=\frac14=0,25$
Zum Zeitpunkt $4$ wächst der Baum um $0,25~m$ pro Woche.
Alle Videos und Lerntexte zum Thema
Videos und Lerntexte zum Thema
Änderungsrate, Differenzenquotient und Differentialquotient (8 Videos, 1 Lerntext)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Änderungsrate, Differenzenquotient und Differentialquotient (8 Arbeitsblätter)
-
 Differenzenquotient bestimmen
PDF anzeigen
Differenzenquotient bestimmen
PDF anzeigen -
 Mittlere Änderungsrate bei Funktionen
PDF anzeigen
Mittlere Änderungsrate bei Funktionen
PDF anzeigen -
 Mittlere Änderungsrate im Sachkontext
PDF anzeigen
Mittlere Änderungsrate im Sachkontext
PDF anzeigen -
 Differentialquotient – Anstieg eines Funktionsgraphen in einem Punkt
PDF anzeigen
Differentialquotient – Anstieg eines Funktionsgraphen in einem Punkt
PDF anzeigen -
 Steigung in einem Punkt
PDF anzeigen
Steigung in einem Punkt
PDF anzeigen -
 Mittlere Änderungsrate – Mit einem Steigungsdreieck bestimmen
PDF anzeigen
Mittlere Änderungsrate – Mit einem Steigungsdreieck bestimmen
PDF anzeigen -
 Mittlere und lokale Änderungsrate
PDF anzeigen
Mittlere und lokale Änderungsrate
PDF anzeigen -
 Mittlere und lokale Änderungsrate – Beispiele
PDF anzeigen
Mittlere und lokale Änderungsrate – Beispiele
PDF anzeigen
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung




















