Mittlere und lokale Änderungsrate


in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
Grundlagen zum Thema Mittlere und lokale Änderungsrate
Zur mittleren Änderungsrate hast du bereits einiges erfahren. So weißt du zum Beispiel, dass man sie verwendet, um Anstiege in bestimmten Intervallen zu berechnen. Darüber hinaus kann man sogar den Anstieg in einem Punkt bestimmen. Dabei hilft dir die lokale Änderungsrate. Du lernst, wie man die lokale Änderungsrate mithilfe der mittleren Änderungsrate berechnen kann und welche Bedeutung sie in Bezug auf ein Anwendungsbeispiel hat. Als Voraussetzung benötigst du nur etwas Wissen zur Grenzwertberechnung.
Transkript Mittlere und lokale Änderungsrate
Hallo, hier ist Mandy. Die mittlere Änderungsrate kennst du ja bereits. Und vielleicht hast du auch schon einmal etwas von der lokalen Änderungsrate gehört. Aber wozu braucht man die beiden Änderungsraten? Und wie berechnet man sie jeweils? Welche Unterschiede und Gemeinsamkeiten gibt es zwischen der mittleren und der lokalen Änderungsrate? All diese Fragen zur mittleren und lokalen Änderungsrate werden wir anhand eines Beispiels untersuchen. Hast du schon von Jordan Romero gehört? Er hat sich vorgenommen, jeweils den höchsten Berg der sieben Kontinente zu besteigen, die sogenannten „Seven Summits“. Und er war gerade einmal 15 Jahre alt, als er auch den letzten Berg von seiner Liste abhaken konnte. Tim bewundert Jordan Romero. Und er hat sich vorgenommen, diese Berge ebenfalls zu besteigen. Er will jedoch zuerst üben und sich auf den Weg machen, den höchsten Berg Deutschlands zu erklimmen, die Zugspitze. Er möchte auf seiner Tour von Hütte zu Hütte wandern, um schrittweise den Gipfel zu erreichen. Dazu will er sich einen Überblick darüber verschaffen, wie groß die Anstiege zwischen den einzelnen Stationen sind. Im Internet hat er sich über das Höhenprofil informiert. Tim möchte an der Ehrwalder Alm bei einer Höhe von 1502 Meter über Normalnull starten. Mögliche Zwischenhalte sind die Hütten „Am Brand“, „Gatterl“, „Knorrhütte“ und „Schneefernerkopf“. Tim kann die Wegstrecken zwischen den Hütten und deren jeweilige Höhenmeter aus dem Höhenprofil ablesen. Mit diesen Angaben kann er nun die Anstiege beziehungsweise die mittlere Änderungsrate in einem bestimmten Intervall bestimmen. Bezogen auf dieses Beispiel bestimmt er die mittlere beziehungsweise durchschnittliche Steigung in dem jeweiligen Streckenabschnitt. Dazu zeichnet Tim Sekanten ein, welche die Zwischenstationen miteinander verbinden. Man berechnet die Steigung der jeweiligen Sekante, weil diese der mittleren Änderungsrate in dem betrachteten Intervall entspricht. Mit Hilfe von Steigungsdreiecken können wir nun schnell den jeweiligen Differenzenquotienten berechnen. Ihn berechnet man durch die folgende Formel, wobei x0 die untere Intervallgrenze bildet und x0+h die obere. Nehmen wir als Beispiel den letzten Streckenabschnitt von Schneefernerkopf bis zur Zugspitze. Dazu zeichnen wir zunächst das Steigungsdreieck ein. Wir betrachten das Intervall von 13200 bis 16200. Mit diesen Werten können wir Δx berechnen. Δy erhalten wir, indem wir die Differenz aus den Höhenmetern der beiden Stationen bilden. Wir rechnen: m im Intervall 13200 bis 16200 ist gleich 2962 minus 2874 geteilt durch 16200 minus 13200, was wiederum 88 geteilt durch 3000 ist. Dies ergibt eine mittlere Änderungsrate von rund 0,03. Das bedeutet, dass man durchschnittlich circa drei Höhenmeter bei einer Distanz von 100 Metern zurücklegt. Wenn wir allerdings genau hinsehen, erkennen wir, dass dieser Wert nicht repräsentativ für diesen Streckenabschnitt ist, da es zunächst steil bergab geht und danach steil bergauf. Diese Anstiege bleiben bei der mittleren Änderungsrate in diesem Intervall unberücksichtigt. Man könnte in einem solchen Fall das Intervall kleiner fassen, um auch die dazwischenliegenden Anstiege zu berücksichtigen. Man könnte das Intervall zum Beispiel in diese abfallende und diese ansteigende Etappe teilen und jeweils die Steigungen berechnen. Man könnte das Intervall sogar so klein fassen, dass man den Anstieg annähernd in einem Punkt bestimmen könnte. Das bezeichnet man dann als lokale Änderungsrate in einem bestimmten Punkt. Beziehungsweise bezogen auf das Beispiel als lokale Steigung an einer Stelle. Allgemein betrachtet können wir nun das Intervall x0 bis x0+h immer kleiner fassen, indem wir h gegen Null streben lassen. Dadurch wird aus grafischer Sicht aus einer Sekante eine Tangente, die also nur noch einen Berührungspunkt mit dem Graphen hat. Und aus rechnerischer Sicht wird der Grenzwert des Differenzenquotienten gebildet. Ihn berechnet man folglich durch diese Formel. Den Grenzwert des Differenzenquotienten bezeichnet man als Differentialquotienten. Er entspricht dem Anstieg der Tangente an der Stelle x0. Wenn man keine Funktionsgleichung gegeben hat, kann man die lokale Änderungsrate aber auch graphisch näherungsweise bestimmen. Dazu nutzt man, wie bei der mittleren Änderungsrate, den Differenzenquotienten. Man berechnet damit allerdings den Anstieg einer Tangente im betrachteten Punkt. Dazu zeichnet man sich in das Diagramm an der betrachteten Stelle zum Beispiel Knorrhütte mit den Koordinaten 7900 und 2051 eine Tangente mit Steigungsdreieck ein. Um den Anstieg an der Stelle 7900 zu berechnen, wählen wir beispielsweise das Intervall 5000 bis 10000, lesen die dazugehörigen Funktionswerte der Tangente ab und setzen diese für Δy und Δx ein. Wir erhalten dann als lokale Änderungsrate etwa den Wert 0,1. In der folgenden Tabelle stellen wir die Unterschiede der mittleren und lokalen Änderungsrate noch einmal zusammen. So verfolgt die mittlere Änderungsrate das Ziel, die mittlere Steigung in einem Intervall zu bestimmen. Die lokale Änderungsrate dagegen ermittelt die lokale Steigung in einem Punkt. Als Formel verwendet man im Allgemeinen für die mittlere Änderungsrate den Differenzenquotienten und für die lokale Änderungsrate den Differentialquotienten. Aus grafischer Sicht entspricht die mittlere Änderungsrate der Steigung einer Sekante. Und die lokale Änderungsrate nähert sich der Steigung an der Tangente an. Auf ein Beispiel angewandt bedeutet die mittlere Änderungsrate, dass man die Durchschnittsgeschwindigkeit eines Läufers in einem Streckenabschnitt, zum Beispiel dem ersten Streckenabschnitt, bestimmt. Mit der lokalen Änderungsrate bestimmt man in diesem Zusammenhang die Geschwindigkeit des Läufers zu dem Zeitpunkt fünf Sekunden nach dem Start. Beide Änderungsraten haben gemeinsam, dass man mit ihnen einen Anstieg ermitteln kann. Nun kann sich Tim gut vorbereitet auf den Weg machen und die höchsten Berge der Welt erklimmen. Was ist mit dir? Überkommt dich jetzt auch die Wanderlust? Das war’s schon wieder von mir. Daher sage ich nun bye bye und bis zum nächsten Mal.
Mittlere und lokale Änderungsrate Übung
-
Ergänze die Erklärung zur mittleren und lokalen Änderungsrate.
TippsDer Name „Differenzenquotient“ rührt daher, dass du den Quotienten aus Differenzen bildest.
Achte bei dem Differenzenquotienten unbedingt auf die Reihenfolge der Subtraktion im Zähler und im Nenner.
LösungIn vielen Zusammenhängen musst du die mittlere Änderungsrate berechnen. Diese wird dir auch in Form von anderen Bezeichnungen begegnen:
- Durchschnittsgeschwindigkeit
- durchschnittliches Wachstum
- mittleres Wachstum
- ...
Du berechnest dann die mittlere Änderungsrate mit Hilfe des Differenzenquotienten:
$m_{[x_0;x_0+h]}=\frac{\Delta y}{\Delta x}=\frac{f(x_0+h)-f(x_0)}{x_0+h-x_0}=\frac{f(x_0+h)-f(x_0)}{h}$.
In manchen Zusammenhängen wird auch nach einer lokalen Änderungsrate oder beispielsweise einer Momentangeschwindigkeit oder dem Wachstum zu einem Zeitpunkt gefragt. Hier geht es immer um den Grenzwert des Differenzenquotienten:
$m_{x_0}=\lim\limits_{h\to 0}\frac{f(x_0+h)-f(x_0)}{h}$.
Dieser Grenzwert wird auch als Differentialquotient bezeichnet.
Das sieht nun sehr kompliziert aus. Hier nun ein Geheimnis: Die lokale Änderungsrate einer Funktion $f$ an der Stelle $x_0$ ist nichts anderes als die Ableitung dieser Funktion an dieser Stelle, also $m_{x_0}=f'(x_0)$.
-
Berechne die mittlere Änderungsrate vom Schneefernerkopf zur Zugspitze.
TippsDie mittlere Änderungsrate in einem Intervall $[a;b]$ kannst du mit der folgenden Formel berechnen:
$m_{\left[a;b\right]}=\frac{f(b)-f(a)}{b-a}$.
Achte auf die Reihenfolge der Differenzen. Die Reihenfolge der Subtraktion im Zähler und im Nenner muss übereinstimmen.
Wenn du zwei Punkte $(5000|3200)$ und $(8000|4700)$ betrachtest, erhältst du als mittlere Änderungsrate
$m_{\left[5000|8000\right]}=\frac{4700-3200}{8000-5000}=\frac{1500}{3000}=\frac12=0,5$.
Das wäre allerdings schon ein ziemlich steiler Anstieg.
LösungTim verwendet die Formel für den Differenzenquotienten, um die mittlere Änderungsrate in einem vorgegebenen Intervall $[x_0;x_0+h]$ zu berechnen:
$m_{\left[x_0;x_0+h\right]}=\frac{\Delta y}{\Delta x}=\frac{f(x_0+h)-f(x_0)}{x_0+h-x_0}=\frac{f(x_0+h)-f(x_0)}{h}$.
Da hier keine Funktion, sondern zwei Punkte gegeben sind, geht er wie folgt vor: $m_{\left[13200;16200\right]}=\frac{2962-2874}{16200-13200}$.
Er dividiert die Differenz der Höhenmeter durch die Differenz der horizontalen Distanzen. Dabei muss er auf die Reihenfolge achten. Hier subtrahiert er von den Höhenmetern der Zugspitze die Höhenmeter des Schneefernerkopfs.
Er rechnet nun weiter: $m_{\left[13200;16200\right]}=\frac{88}{3000}\approx 0,03$.
Das bedeutet, dass er bei einer horizontalen Distanz von $100$ Metern $3~\text{m}$ Höhenmeter zurücklegt.
-
Berechne die mittlere Änderungsrate von $f$ bei gegebenem Intervall.
TippsVerwende für die mittlere Änderungsrate die Formel
$m_{[x_0;x_0+h]}=\frac{\Delta y}{\Delta x}=\frac{f(x_0+h)-f(x_0)}{x_0+h-x_0}=\frac{f(x_0+h)-f(x_0)}{h}$.
In dieser Aufgabe ist $x_0=0$. Der Summand $h$ ändert sich jeweils.
Schau dir ein Beispiel an für das Intervall $[0;0,1]$.
$m_{[0;0,1]}=\frac{f(0,1)-f(0)}{0,1}=\frac{2,21-2}{0,1}=2,1$
LösungIm Folgenden verwendest du für die Berechnung der mittleren Änderungsrate immer die Formel
$m_{[x_0;x_0+h]}=\frac{\Delta y}{\Delta x}=\frac{f(x_0+h)-f(x_0)}{x_0+h-x_0}=\frac{f(x_0+h)-f(x_0)}{h}$.
Dabei ist $x_0=0$.
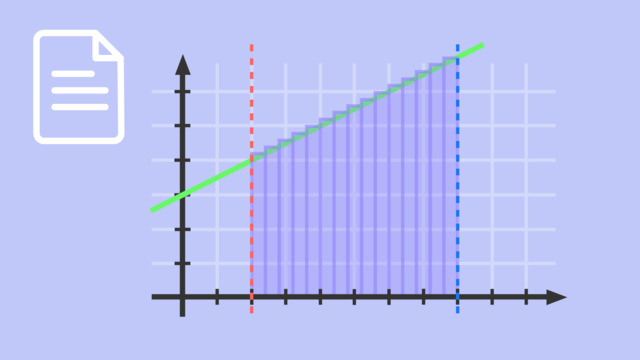
- $m_{[0;1]}=\frac{f(1)-f(0)}{1}=\frac{5-2}1=3$: Diese Steigung kannst du in dem nebenstehenden Bild erkennen.
- $m_{[0;0,8]}=\frac{f(0,8)-f(0)}{0,8}=\frac{4,24-2}{0,8}=2,8$
- $m_{[0;0,6]}=\frac{f(0,6)-f(0)}{0,6}=\frac{3,56-2}{0,6}=2,6$
- $m_{[0;0,4]}=\frac{f(0,4)-f(0)}{0,4}=\frac{2,96-2}{0,4}=2,4$
- $m_{[0;0,2]}=\frac{f(0,2)-f(0)}{0,2}=\frac{2,44-2}{0,2}=2,2$
-
Leite die lokale Änderungsrate an der Stelle $x_0=0$ her.
TippsDie lokale Änderungsrate ist definiert als der Grenzwert des Differenzenquotienten.
Die lokale Änderungsrate $m_{x_0}$ an der Stelle $x_0$ ist gegeben durch die folgende Beziehung:
$m_{x_0}=\lim\limits_{h\to 0}\frac{f(x_0+h)-f(x_0)}{h}$.
LösungWenn du ganz genau hinschaust, kannst du hier bereits die lokale Änderungsrate erkennen. Diese ist $m_0=2$.
Nur leider ist es in der Mathematik nicht üblich, Ergebnisse abzulesen. Abgesehen davon, ist ein solches Vorgehen meist zu ungenau.
Die lokale Änderungsrate ist allgemein gegeben durch den Grenzwert des Differenzenquotienten:
$m_{x_0}=\lim\limits_{h\to 0}\frac{f(x_0+h)-f(x_0)}{x_0+h-x_0}=\lim\limits_{h\to 0}\frac{f(x_0+h)-f(x_0)}{h}$.
In unserem Beispiel mit $x_0=0$ vereinfacht sich die Formel für die lokale Änderungsrate zu:
$m_{0}=\lim\limits_{h\to 0}\frac{f(h)-f(0)}{h}$.
Wir schauen uns zunächst den Quotienten an:
$\frac{f(h)-f(0)}{h}=\frac{h^2+2h+2-2}{h}=\frac{h^2+2h}{h}=\frac{h(h+2)}{h}=h+2$.
Nun kannst du den Grenzwert bestimmen:
$m_{0}=\lim\limits_{h\to 0}\frac{f(h)-f(0)}{h}=\lim\limits_{h\to 0}(h+2)=2$.
Du kannst die lokale Änderungsrate auch so berechnen:
- Du bestimmst die erste Ableitung der Funktion $f$. Diese ist $f'(x)=2x+2$.
- Dann ist $m_0=f'(0)=2\cdot 0+2=2$.
-
Beschreibe den Unterschied zwischen der mittleren und der lokalen Änderungsrate.
TippsMit Hilfe eines Steigungsdreiecks kannst du die Steigung einer Geraden durch zwei Punkte berechnen. Hier ist
$m=\frac{1-4}{0-(-4)}=-\frac34$.
- Eine Sekante schneidet den Graphen einer Funktion in (mindestens) zwei Punkten.
- Eine Tangente berührt den Graphen einer Funktion in einem Punkt.
Die mittlere Änderungsrate einer Funktion $f$ in dem Intervall $[a;b]$ ist wie folgt definiert:
$m_{\left[a;b\right]}=\frac{\Delta y}{\Delta x}=\frac{f(b)-f(a)}{b-a}$
Sie beschreibt die mittlere Steigung in einem Streckenabschnitt.
Die lokale Änderungsrate beschreibt die lokale Steigung an einer Stelle.
LösungWas ist der Unterschied zwischen einer mittleren und einer lokalen Änderungsrate?
Zur Berechnung der mittleren Änderungsrate einer Funktion $f$ benötigst du ein Intervall $[a;b]$ oder gerne auch $[x_0;x_0+h]$. Nun berechnest du die mittlere Änderungsrate:
$m_{[x_0;x_0+h]}=\frac{\Delta y}{\Delta x}=\frac{f(x_0+h)-f(x_0)}{x_0+h-x_0}=\frac{f(x_0+h)-f(x_0)}{h}$.
Da du hier den Quotienten zweier Differenzen bildest, wird dieser auch als Differenzenquotient bezeichnet.
Anschaulich entspricht die mittlere Änderungsrate in einem Intervall der Steigung einer Sekante, hier grün eingezeichnet.
Die lokale Änderungsrate ergibt sich als Grenzwert der mittleren Änderungsrate:
$m_{x_0}=f'(x_0)=\lim\limits_{h\to 0}\frac{f(x_0+h)-f(x_0)}{h}$.
Die lokale Änderungsrate wird auch als Differentialquotient bezeichnet. Anschaulich entspricht diese der Steigung einer Tangente, hier rot eingezeichnet.
Die Schreibweise $f'(x_0)$ kennst du vielleicht bereits oder lernst sie sehr bald kennen. Der Strich steht für die Ableitung.
-
Ermittle die Stelle $x_0$, an welcher die lokale Änderungsrate so groß ist wie die mittlere Änderungsrate auf dem Intervall $[-1;2]$.
TippsVerwende die folgende Definition für die mittlere Änderungsrate:
$m_{[x_0;x_0+h]}=\frac{\Delta y}{\Delta x}=\frac{f(x_0+h)-f(x_0)}{h}$.
Die mittlere Änderungsrate ist eine natürliche Zahl.
Es ist $m_{x_0}=\lim\limits_{h\to 0}\frac{(x_0+h)^2+2(x_0+h)+2-(x_0^2+2x_0+2)}{h}$ die lokale Änderungsrate.
Verwende die erste binomische Formel $(x_0+h)^2=x_0^2+2x_0h+h^2$.
LösungZunächst berechnest du die mittlere Änderungsrate für die Funktion $f$ mit $f(x)=x^2+2x+2$ auf dem gegebenen Intervall $[-1;2]$. Es ist also $x_0=-1$ und $h=3$.
Damit ist
$m_{[-1;-1+3]}=\frac{\Delta y}{\Delta x}=\frac{f(-1+3)-f(-1)}{3}=\frac{f(2)-f(-1)}{3}$.
Berechne zunächst die Funktionswerte
- $f(-1)=(-1)^2+2\cdot (-1)+2=1$ und
- $f(2)=2^2+2\cdot 2+2=10$.
Die lokale Änderungsrate ist allgemein gegeben durch den Grenzwert des Differenzenquotienten:
$m_{x_0}=\lim\limits_{h\to 0}\frac{f(x_0+h)-f(x_0)}{x_0+h-x_0}=\lim\limits_{h\to 0}\frac{f(x_0+h)-f(x_0)}{h}$.
Dieser Grenzwert wird im Folgenden für die Funktion $f$ mit $f(x)=x^2+2x+2$ hergeleitet.
$\begin{array}{rclll} m_{x_0}&=&\lim\limits_{h\to 0}\frac{(x_0+h)^2+2(x_0+h)+2-(x_0^2+2x_0+2)}{h}&|&\text{1. binomische Formel}\\ &=&\lim\limits_{h\to 0}\frac{x_0^2+2x_0h+h^2+2x_0+2h+2-x_0^2-2x_0-2}{h}\\ &=&\lim\limits_{h\to 0}\frac{2x_0h+h^2+2h}{h}\\ &=&\lim\limits_{h\to 0}\frac{h(2x_0+h+2)}{h}\\ &=&\lim\limits_{h\to 0}(2x_0+h+2) \end{array}$
Zuletzt berechnest du den Grenzwert:
$m_{x_0}=\lim\limits_{h\to 0}(2x_0+h+2)=2x_0+2$.
Es muss also für $x_0$ gelten: $2x_0+2=3$.
- Subtrahiere $2$ auf beiden Seiten der Gleichung, so erhältst du $2x_0=1$.
- Dividiere nun beide Seiten der Gleichung durch $2$. So kommst du zu $x_0=\frac12=0,5$.

Differenzenquotient bestimmen

Mittlere Änderungsrate bei Funktionen

Mittlere Änderungsrate im Sachkontext

Differentialquotient – Anstieg eines Funktionsgraphen in einem Punkt

Steigung in einem Punkt

Mittlere Änderungsrate – Mit einem Steigungsdreieck bestimmen

Mittlere und lokale Änderungsrate

Mittlere und lokale Änderungsrate – Beispiele
Analysis
9.931
sofaheld-Level
6.600
vorgefertigte
Vokabeln
8.313
Lernvideos
38.641
Übungen
33.706
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Klassenstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung




 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?









Ich finde den Begriff "lokale Änderungsrate" viel verständlicher. Mit dem Beispiel kann ich's mir bildlicher Vorstellen als mit dem anderen Begriff.
sehr gutes Video, Mandy!
@Rau Anja: Genau ... die lokale Änderungsrate ist nur ein anderer Begriff für momentane Änderungsrate.
Oder ist das die lokale Änderungsrate?
Könnten Sie auch ein Video zur momentanen Änderungsrate machen?