Cramersche Regel
Die Cramersche Regel ist eine Methode zur Lösung von linearen Gleichungssystemen. Ihr Name stammt von Gabriel Cramer und sie basiert auf Determinanten und Matrizen. Finde heraus, wie man die Regel anwendet und erhalte Erklärungen und Beispiele in unserem Video! Interessiert? All das und noch mehr kannst du im folgenden Text entdecken.
in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.

Grundlagen zum Thema Cramersche Regel
Die cramersche Regel für lineare Gleichungssysteme
Wir kennen bereits verschiedene Methoden, wie beispielsweise das Additionsverfahren oder das Gleichsetzungsverfahren, mit deren Hilfe wir lineare Gleichungssysteme lösen können. Die cramersche Regel ist ein weiteres solches Verfahren. Sie wurde nach dem Mathematiker Gabriel Cramer benannt, der sie im Jahr 1750 in einem Buch erklärte. Wir wollen uns im Folgenden damit auseinandersetzen, wie die cramersche Regel funktioniert, und ein Beispiel berechnen. Dazu solltest du schon wissen, was eine Matrix ist und wie man eine Determinante berechnet. Wir schauen uns zunächst die Definition der cramerschen Regel für ein lineares Gleichungssystem mit zwei Unbekannten an und betrachten im Anschluss die Anwendung an einem Beispiel.
Was ist die cramersche Regel?
Wir betrachten ein lineares Gleichungssystem mit zwei Unbekannten und zwei Gleichungen der Form:
$a_{11}x + a_{12}y = b_1$
$a_{21}x + a_{22}y = b_2$
Gesucht sind diejenigen Werte für $x$ und $y$, die beide Gleichungen erfüllen. Die linke Seite der beiden Gleichungen können wir in Form einer Matrix, genauer gesagt als Koeffizientenmatrix, darstellen. Die Einträge dieser Matrix sind die Koeffizienten der beiden linearen Gleichungen. Diese Matrix $A$ sieht dann wie folgt aus:
$A = \begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix}$
Die rechte Seite kann als Vektor der folgenden Form dargestellt werden:
$\vec{b} = \begin{pmatrix} b_1 \\ b_2 \end{pmatrix}$
Außerdem definieren wir zwei weitere Matrizen, die wir für die cramersche Regel brauchen. Dazu ersetzen wir einmal die erste Spalte der Matrix $A$ durch den Vektor $\vec{b}$, um die Matrix $A_x$ zu erhalten, und einmal die zweite Spalte, um die Matrix $A_y$ zu erhalten:
$A_x = \begin{pmatrix} b_1 & a_{12} \\ b_2 & a_{22} \end{pmatrix}$
und
$A_y = \begin{pmatrix} a_{11} & b_1 \\ a_{21} & b_2 \end{pmatrix}$
Damit haben wir alle Begriffe eingeführt, die wir für die Definition der Werte $x$ und $y$ nach der cramerschen Regel benötigen. Für diese gilt dann:
$x = \frac{\text{det}(A_x)}{\text{det}(A)}$
und
$y = \frac{\text{det}(A_y)}{\text{det}(A)}$
Dabei zeigt $\text{det}$ an, dass die Determinante der jeweiligen Matrix berechnet werden muss. (Manchmal wird die Determinante auch durch vertikale Striche angezeigt, zum Beispiel:
Wie wendet man die cramersche Regel an?
Als Beispiel für die cramersche Regel betrachten wir das folgende Gleichungssystem:
$2x + 3y = 4$
$5x + 6y = 7$
Zunächst müssen wir die Koeffizientenmatrix $A$ und den Vektor $\vec{b}$ bestimmen. Dazu vergleichen wir einfach unser Gleichungssystem mit der Definition der cramerschen Regel und identifizieren die Koeffizienten $a_{11}$, $a_{12}$ und so weiter. Damit erhalten wir:
$A = \begin{pmatrix} 2 & 3 \\ 5 & 6 \end{pmatrix}$
und
$\vec{b} = \begin{pmatrix} 4 \\ 7 \end{pmatrix}$
Mit $A$ und $\vec{b}$ können wir nun die Matrizen $A_x$ und $A_y$ bestimmen, indem wir $\vec{b}$ jeweils für die erste bzw. zweite Spalte der Matrix $A$ einsetzen. Damit erhalten wir die folgenden Matrizen:
Einsetzen von $\vec{b}$ als erste Spalte der Matrix $A$:
$A_x = \begin{pmatrix} 4 & 3 \\ 7 & 6 \end{pmatrix}$
Einsetzen von $\vec{b}$ als zweite Spalte der Matrix $A$:
$A_y = \begin{pmatrix} 2 & 4 \\ 5 & 7 \end{pmatrix}$
Jetzt müssen wir die Determinanten der Matrizen $A$, $A_x$ und $A_y$ berechnen. Dazu nutzen wir die Formel zur Berechnung der Determinante von $(2 \times 2)$-Matrizen:
$\text{det}(A) = a_{11} \cdot a_{22} - a_{21} \cdot a_{12}$
Du kannst diese Regel in unserem Video zur Determinante von $(2 \times 2)$-Matrizen wiederholen, falls du sie vergessen hast. An dieser Stelle wenden wir die Regel einfach an, indem wir die Werte für die einzelnen Matrizen einsetzen:
$\text{det}(A) = 2 \cdot 6 - 5 \cdot 3 = 12 - 15 = -3$
$\text{det}(A_x) = 4 \cdot 6 - 7 \cdot 3 = 24 - 21 = 3$
$\text{det}(A_y) = 2 \cdot 7 - 5 \cdot 4 = 14 - 20 = -6$
Diese Werte setzen wir nun in die Gleichungen für $x$ und $y$ ein:
$x = \frac{3}{-3} = -1$
$y = \frac{-6}{-3} = 2$
Um unser Ergebnis zu überprüfen, setzen wir die ermittelten Werte in unser Gleichungssystem ein:
$4 = 2x + 3y = 2 \cdot (-1) + 3 \cdot 2 = -2 + 6 =4$
$7 = 5x + 6y = 5 \cdot (-1) + 6 \cdot 2 = -5 + 12 = 7$
In beiden Fällen ergibt sich eine wahre Aussage, das Ergebnis ist also korrekt.
Cramersche Regel – Verallgemeinerung
In unserer Erklärung zur cramerschen Regel haben wir die Definition anhand eines linearen Gleichungssystems mit zwei Gleichungen und zwei Unbekannten eingeführt. Die cramersche Regel kann auch bei beliebig vielen Unbekannten angewendet werden. Dabei müssen immer zwei Bedingungen erfüllt sein:
- Es muss genauso viele Unbekannte wie Gleichungen geben, sodass die Koeffizientenmatrix $A$ quadratisch ist.
- Die Determinante der Matrix $A$ darf nicht null sein, da wir durch $\text{det}A$ teilen müssen.
Cramersche Regel – Zusammenfassung
Wir fassen die wichtigsten Punkte noch einmal zusammen:
- Die cramersche Regel wurde im Jahr 1750 von Gabriel Cramer entwickelt.
- Mithilfe der cramerschen Regel können lineare Gleichungssysteme gelöst werden, die genauso viele Gleichungen wie Unbekannte haben.
- Die Determinante der Koeffizientenmatrix $A$ darf nicht null sein.
In diesem Video wird dir die cramersche Regel einfach erklärt. Dir wird außerdem der Rechenweg anhand eines Beispiels gezeigt. Video und Text werden durch interaktive Übungen und Aufgaben ergänzt.
Transkript Cramersche Regel
Hallo, mein Name ist Kathleen und ich möchte dir eine weitere Methode zeigen, wie du ganz einfach und schnell ein lineares Gleichungssystem mit zwei Unbekannten lösen kannst. Also, wie löst man ein lineares System super schnell und einfach? Diese Methode ist so genial, dass sie sogar einen eigenen Namen erhalten hat, mit der „Cramerschen Regel“, auch genannt die Determinantenmethode. Du kennst bereits Methoden, um lineare Gleichungssysteme zu lösen. Welche Methoden fallen dir spontan ein? Methoden, die du bereits kennst, sind das Additionsverfahren, das Einsetzungsverfahren, das Gleichsetzungsverfahren und das graphische Lösen. Der Rechenaufwand und die Schreibarbeit ist bei diesen Methoden sehr hoch und man kann sich schnell verrechnen. Genau deswegen lohnt es sich, noch eine fünfte Methode kennenzulernen. Aber um die super schnelle Methode, genannt die Cramersche Regel, anwenden zu können, musst du erstmal ein paar neue Begriffe kennenlernen. Dieser kleine Arbeitseinsatz lohnt sich allemal. Ich werde mich dabei sehr kurz fassen und dir nur das nötigste, also das, was du zum Verständnis brauchst, näherbringen. Die neuen Begriffe, die es zu klären gilt, sind: Was ist eine Matrix? Was ist eine Determinante? Um die neuen Begriffe klären zu können, brauchst du ein lineares Gleichungssystem mit zwei Unbekannten. Diese Unbekannten bezeichnet man in der Regel mit x und y. Jetzt noch zwei lineare Gleichungen. Die erste Gleichung 2x + 3y = 4 und die zweite, da du zwei Unbekannte ausrechnen musst, brauchst du auch zwei Gleichungen. 5x + 6y = 7. Verbindet man die zwei linearen Gleichungen mit den Variablen x und y durch ein „und“, so erhält man ein lineares Gleichungssystem. Und die gesuchte Lösungsmenge ist x, y. Jetzt will ich erstmal mit dir die neuen Begriffe angehen. Die erste Frage, die es zu beantworten gilt, lautet „Was ist eine Matrix?“ Eine Matrix ist einfach nur eine andere Schreibweise für ein lineares Gleichungssystem. Eine Art Tabelle, in der Zahlen stehen. Das spart viel Schreibarbeit. Diese Zahlen nennt man Koeffizienten oder Einträge der Matrix. Eine Matrix bezeichnet man immer mit Großbuchstaben, zum Beispiel groß A. Wie sieht so eine Matrix aus? Eine Tabelle besteht aus Zeilen und Spalten, so auch eine Matrix. Welche Zahlen trägt man in die Spalte ein? Nehmen wir das Beispiel von eben. Vor der Unbekannten x steht in der ersten linearen Gleichung eine zwei und in der zweiten steht vor dem x eine fünf. Und vor dem y stehen die Zahlen drei und sechs. In die Matrix A trage ich die Zahlen zwei und fünf in die erste Spalte ein. In die zweite Spalte schreibe ich die Zahlen, die vor der Unbekannten y stehen, also drei und sechs. Jetzt ist die Matrix fast fertig. Es fehlt noch eine runde Klammer um die Matrix abzugrenzen und fertig ist eine 2x2-Matrix, auch bezeichnet als quadratische Matrix. 2x2 bedeutet, dass die Matrix zwei Zeilen und zwei Spalten hat. Welche Einträge stehen in der ersten Zeile? Die Zwei und die Drei. Und in der zweiten Zeile? Die Fünf und die Sechs. Zu einer Matrix gehört noch die Hauptdiagonale, in dieser stehen die Elemente zwei und sechs. Und die Nebendiagonale mit den Einträgen fünf und drei. Die Matrix A ist noch unvollständig, es fehlen ja noch die Zahlen vier und sieben aus dem Gleichungssystem. Ich stelle eine weitere Matrix auf und nenne diese B. Die Zahlen vier und sieben bilden die dritte Spalte. B besteht aus zwei Zeilen und drei Spalten. B ist eine 2x3-Matrix, also nicht quadratisch. Solche Matrizen, ja die Matrix ist Matrizen, vereinfachen das mathematische Leben ungemein. Für dich in diesem Fall wird das Lösen von Gleichungen vereinfacht. Wie? Das führt uns direkt zu dem zweiten neuen Begriff, den du kennenlernst. Was ist eine Determinante? Das ist nicht ganz so leicht zu beantworten wie der Begriff der Matrix, aber ich beschränke mich hier auf das Wesentliche. Die Determinante ist die Maßzahl einer quadratischen Matrix. Was bedeutet das? Man kann die Matrix ausrechnen und erhält eine Determinante, also wieder eine reelle Zahl. In unserem Fall werden aus den vier Einträgen in der Matrix A nach einer bestimmten Rechenvorschrift genau eine Zahl und diese Zahl nennt man Determinante. Man schreibt einfach D oder det(A). Wie berechnet man die Determinante einer 2x2-Matrix? Mit einer mathematischen Formel. Man erhält den Wert einer Determinante, indem man das Produkt der Hauptdiagonalelemente minus dem Produkt der Nebendiagonalelemente bildet. Ich werde die Determinante A einmal an unserem Beispiel vorrechnen. Für A setze ich unsere Matrix A ein. Die Elemente in der Hauptdiagonale sind zwei und sechs. Die Einträge müssen multipliziert werden, also 2 * 6. Die Elemente der Nebendiagonale sind drei und fünf, also - 3 * 5. Das Produkt der Hauptdiagonale ist zwölf, davon soll das Produkt der Nebendiagonale, also 15, abgezogen werden. Das ergibt minus drei. Der Wert der Determinante der Matrix A ist gleich minus drei. Wozu brauchst du das alles? Das führt uns endlich zur Cramerschen Regel. Gabriel Cramer war vor 300 Jahren Professor der Mathematik an der Universität Genf. Nach dieser langen Einführung geht das jetzt, wie versprochen, ganz schnell. Die Cramersche Regel ist ein Algorithmus, also ein systematisches Verfahren, um x und y zu bestimmen. So einfach sieht die Regel aus: Um x zu bestimmen, bildet man den Quotienten aus der Determinante Ax und der Determinante A. Für y genau das gleiche, man benötigt die Determinante Ay und dividiert diese durch die Determinante A. Wie bestimmt man jetzt die Determinanten Ax und Ay? Genauso wie Determinante A. Die Determinante A haben wir bereits nach der Rechenregel ausgerechnet. det(A) = -3. Betrachte dir noch einmal die Matrix B. B hat zwei Zeilen mit den Einträgen zwei, drei und vier und fünf, sechs und sieben und drei Spalten. Die Rechenregel kann man nur bei 2x2-Matrizen anwenden, aber nicht bei der 2x3-Matrix B. Um Determinante Ax auszurechnen, vertauscht man die erste Spalte, also die Einträge zwei und fünf mit der dritten Spalte, vier und sieben. Ich nenne die Matrix Bx, da das x auszurechnen ist. Für die Determinante Ax betrachtet man nur die 2x2-Matrix mit den Einträgen vier und drei in der ersten Zeile und sieben und sechs in der zweiten Zeile. Nach der Rechenvorschrift für Determinanten erhält man den Wert drei. In die Cramersche Regel setze ich den Wert der Determinante Ax, also drei ein und für Determinante A minus drei. Man erhält den Quotienten 3/-3, fertig ist die Lösung für x. x = -1. Für die Determinante Ay vertauscht man die Einträge der zweiten Spalte mit der dritten Spalte. Diese Matrix nenne ich By. Für die Determinante Ay betrachten wir wie eben nur die 2x2-Matrix mit den Einträgen zwei und vier in der ersten Zeile und fünf und sieben in der zweiten Zeile. Man rechnet ganz schnell die Determinante Ay aus. Der Wert der Determinante Ay ist minus sechs. In die Cramersche Regel setzen wir die Werte minus sechs und minus drei ein und man erhält die Lösung für y. y = 2. Die erhaltene Lösungsmenge mit der Cramerschen Regel ist für x = -1 und y = 2. Es ist immer ratsam, die erhaltene Lösungsmenge durch eine Probe zu bestätigen, führen wir zum Schluss noch schnell die Probe durch. Das x wird in der ersten und zweiten Gleichung durch minus eins ersetzt und das y durch die zwei. Es gilt Punkt-vor-Strich-Rechnung, also in der ersten Gleichung 2 * (-1) = -2 und 3 * 2 = 6. In der zweiten Gleichung 5 * (-1) = -5 und 6 * 2 = 12. -2 + 6 = 4, 4 = 4. -5 + 12 = 7, 7 = 7, ist eine wahre Aussage. Also ist die Lösungsmenge minus eins und zwei bestätigt. Schön, dass du so lange durchgehalten hast, du hast aber auch eine Menge nützlicher neuer mathematischer Begriffe kennengelernt: Du weißt jetzt, was ist eine Matrix, wie man einer 2x2-Matrix den Wert der Determinante ausrechnet und vor allem die Cramersche Regel, die das Lösen von linearen Gleichungssystemen stark vereinfacht. Viel Erfolg beim Rechnen, tschüss sagt Kathleen!
Cramersche Regel Übung
-
Bestimme die $2~$x$~3$ Matrizen zu den gegebenen Gleichungssystemen.
TippsEine $2~$x$~3$ Matrix besteht aus zwei Zeilen und drei Spalten.
In die erste Spalte schreiben wir die Koeffizienten der Variable x und in die zweiten Spalte die Koeffizienten der Variable y. In die dritten Spalte schreiben wir die Zahlen, die auf der rechten Seite der Gleichungen stehen.
LösungEine Matrix ist eine Art Tabelle, in der Zahlen stehen. Diese Zahlen nennt man Koeffizienten oder Einträge der Matrix.
Ein Matrix bezeichnet man mit Großbuchstaben z.B.: A, B oder C
Eine Matrix besteht aus Zeilen und Spalten.
Eine $2~$x$~3$ Matrix besteht aus zwei Zeilen und drei Spalten.
Beispiel:
$\begin{align} &\text{I}& 2x+3y&=4 \\ &\text{II}& 5x+6y&=7 \\ \end{align}$
$ B= \begin{pmatrix} 2 & 3 & 4 \\ 5 & 6 & 7 \end{pmatrix} $
In die erste Spalte schreiben wir die Koeffizienten der Variable x und in die zweiten Spalte die Koeffizienten der Variable y. In die dritten Spalte schreiben wir die Zahlen vier und sieben.
Eine $2~$x$~2$ Matrix bezeichnen wir als quadratische Matrix. Hierbei bezeichnen wir die Diagonale von oben links nach unten rechts als Hauptdiagonale und die Diagonale von unten links nach oben rechts als Nebendiagonale.
Die weiteren Lösungen sind:
$\begin{align} &\text{I}& 3x+6y&=0 \\ &\text{II}& 1x+8y&=3 \\ \end{align}$
$~$
$~~~~~~B=\begin{pmatrix} 3 & 6 & 0 \\ 1 & 8 & 3 \end{pmatrix}$
______________________________________________
$\begin{align} &\text{I}& 1000x+500y&=15 \\ &\text{II}& 1x+5y&=1 \\ \end{align}$
$~$
$~~~~~~B=\begin{pmatrix} 1000 & 500 & 15 \\ 1 & 5 & 1 \end{pmatrix}$
______________________________________________
$\begin{align} &\text{I}& 1x+1y&=1 \\ &\text{II}& 1x+1y&=1 \\ \end{align}$
$~$
$~~~~~~B=\begin{pmatrix} 1 & 1 & 1 \\ 1 & 1 & 1 \end{pmatrix}$
-
Gib an, wie man den Wert einer Determinante berechnet.
TippsDas Ergebnis einer Matrix ist eine reelle Zahl. Diese Zahl nennt man Determinante.
$ \begin{vmatrix} a & b \\ c & d \end{vmatrix} =a \cdot d - c \cdot b$
LösungEine Determinante ist die Maßzahl einer $2$ x $2$ Matrix.
Das Ergebnis einer Matrix ist eine reelle Zahl. Diese Zahl nennt man Determinante.
Wir benennen eine Determinante mit D oder det A.
Man erhält den Wert einer Determinante, wenn man das Produkt der Hauptdiagonalelemente minus dem Produkt der Nebendiagonalelemente einer quadratischen $2$ x $2$ Matrix rechnet.
$ \begin{vmatrix} a & b \\ c & d \end{vmatrix} =a \cdot d - c \cdot b$
Beispiel:
Wir haben eine $2$ x $2$ Matrix gegeben: $A= \begin{pmatrix} 2 & 3 \\ 5 & 6 \end{pmatrix} $
$det~A=det \begin{pmatrix} 2 & 3 \\ 5 & 6 \end{pmatrix}=2 \cdot 6 - 5 \cdot 3=12-15=-3$
-
Berechne die Werte der Determinanten $A$, $A_x$ und $A_y$.
TippsZunächst bilden wir die Matrizen $B_x$ und $B_y$.
$B_x= \begin{pmatrix} 4 & 3 & 2 \\ 7 & 6 & 5 \end{pmatrix}$
$B_y= \begin{pmatrix} 2 & 4 & 3 \\ 5 & 7 & 6 \end{pmatrix}$
Aus den Matrizen $B$, $B_x$ und $B_y$ bestimmen wir die quadratischen $2~$x$~2$ Matrizen $A$, $A_x$ und $A_y$. Diese bestehen jeweils aus den ersten beiden Zeilen und Spalten der zugehörigen $2~$x$~2$ Matrix.
Schließlich erhalten wir die Werte für die Determinanten der drei Matrizen durch Anwenden der Formel zur Berechnung einer Determinante:
$ \begin{vmatrix} a & b \\ c & d \end{vmatrix} =a \cdot d - c \cdot b$
LösungWir haben die $2~x~3$ Matrix gegeben:
$B= \begin{pmatrix} 2 & 3 & 4 \\ 5 & 6 & 7 \end{pmatrix}$
Zu dieser Matrix sollen nun die Determinanten $A$, $A_x$ und $A_y$ bestimmt werden.
Zunächst bilden wir die Matrizen $B_x$ und $B_y$.
Matrix $B_x$ bestimmen wir, indem wir die erste Spalte mit der letzten Spalte der Matrix $B$ vertauschen. Wir erhalten demnach folgende Matrix:
$B_x= \begin{pmatrix} 4 & 3 & 2 \\ 7 & 6 & 5 \end{pmatrix}$
Matrix $B_y$ bestimmen wir, indem wir die zweite Spalte mit der letzten Spalte der Matrix $B$ vertauschen. Wir erhalten demnach folgende Matrix:
$B_y= \begin{pmatrix} 2 & 4 & 3 \\ 5 & 7 & 6 \end{pmatrix}$
Aus den Matrizen $B$, $B_x$ und $B_y$ bestimmen wir die quadratischen $2~x~2$ Matrizen $A$, $A_x$ und $A_y$.
$A= \begin{pmatrix} 2 & 3 \\ 5 & 6 \end{pmatrix}$
$A_x= \begin{pmatrix} 4 & 3 \\ 7 & 6 \end{pmatrix}$
$A_y= \begin{pmatrix} 2 & 4 \\ 5 & 7 \end{pmatrix}$
Schließlich erhalten wir die Werte für die Determinanten der drei Matrizen durch Anwenden der Formel zur Berechnung einer Determinante:
$ \begin{vmatrix} a & b \\ c & d \end{vmatrix} =a \cdot d - c \cdot b$
$det~A=\begin{vmatrix} 2 & 3 \\ 5 & 6 \end{vmatrix}=2 \cdot 6- 5 \cdot 3=12-15=-3$
$det~A_x=\begin{vmatrix} 4 & 3 \\ 7 & 6 \end{vmatrix}=4 \cdot 6 - 7 \cdot 3 = 24 - 21=3$
$det~A_y=\begin{vmatrix} 2 & 4 \\ 5 & 7 \end{vmatrix}=2 \cdot 7 - 5 \cdot 4 = 14 - 20 = -6$
-
Berechne x und y mit der Cramerschen Regel
TippsDie Cramersche Regel zum Lösen eines linearen Gleichungssystems lautet:
$x=\frac{det~A_x}{det~A}~~~~y=\frac{det~A_y}{det~A}$
$det~A=det \begin{pmatrix} 1 & 3 \\ 2 & 4 \end{pmatrix}$
$det~A_x=det \begin{pmatrix} 5 & 3 \\ 6 & 4 \end{pmatrix}$
$det~A_y=det \begin{pmatrix} 1 & 5 \\ 2 & 6 \end{pmatrix}$
$det~A=det \begin{pmatrix} 1 & 3 \\ 2 & 4 \end{pmatrix}=1 \cdot 4 - 2 \cdot 3=4 - 6=-2$
$det~A_x=det \begin{pmatrix} 5 & 3 \\ 6 & 4 \end{pmatrix}=5 \cdot 4 - 6 \cdot 3=20 - 18=2$
$det~A_y=det \begin{pmatrix} 1 & 5 \\ 2 & 6 \end{pmatrix}=1 \cdot 6 - 2 \cdot 5=6 - 10=-4$
LösungGegeben ist folgendes lineares Gleichungssystem:
$\begin{align} &\text{I}& 1x+3y&=5 \\ &\text{II}& 2x+4y&=6 \\ \end{align}$
Wir wollen die Lösungsmenge $L=\{(x;y)\}$ mit der Cramerschen Regel berechnen.
Die Cramersche Regel zum Lösen eines linearen Gleichungssystems lautet:
$x=\frac{det~A_x}{det~A}~~~~y=\frac{det~A_y}{det~A}$
Wir benötigen also die Werte der Determinanten $A$, $A_x$ und $A_y$.
Aus dem linearen Gleichungssystem können wir die Determinanten bestimmen.
$det~A=det \begin{pmatrix} 1 & 3 \\ 2 & 4 \end{pmatrix}=1 \cdot 4 - 2 \cdot 3=4 - 6=-2$
$det~A_x=det \begin{pmatrix} 5 & 3 \\ 6 & 4 \end{pmatrix}=5 \cdot 4 - 6 \cdot 3=20 - 18=2$
$det~A_y=det \begin{pmatrix} 1 & 5 \\ 2 & 6 \end{pmatrix}=1 \cdot 6 - 2 \cdot 5=6 - 10=-4$
Nun müssen wir nur noch die Werte der Determinanten in die Cramersche Regel einsetzen und so erhalten wir die Lösungsmenge $L=\{(x;y)\}$.
$\Rightarrow x=\frac{2}{-2}=-1$
$\Rightarrow y=\frac{-4}{-2}=2$
Die Lösungsmenge ist demnach $L=\{(-1;2)\}$.
-
Gib an, welche Methoden es neben dem Determinantenmethode noch gibt, um ein lineares Gleichungssystem zu lösen.
TippsDer Satz des Pythagoras wird u.a. in der Geometrie benutzt, um einen rechten Winkel zu konstruieren.
Eine quadratische Ergänzung hilft uns in der Mathematik eine quadratische Gleichung zu lösen.
LösungUm ein lineares Gleichungssystem zu lösen, kennen wir bereits folgende Methoden:
- Additionsverfahren
- Einsetzungsverfahren
- Gleichsetzungsverfahren
- Graphisches Lösen
Eine quadratische Ergänzung hilft uns in der Mathematik eine quadratische Gleichung zu lösen.
Neben den genannten Methoden zum Lösen eines linearen Gleichungssystems, lernst du heute eine neue Methode kennen: Die Cramersche Regel. Sie ist bedeutend schneller und es können nicht so viele Rechenfehler passieren.
-
Bestimme das zur Lösungsmenge passende Gleichungssystem.
TippsSetze der Reihe nach die x und y Werte in die Gleichungssysteme ein. In welchem Gleichungssystem erhältst du eine wahre Aussage?
Alternativ kannst du auch jeweils die Cramersche Regel anwenden und die Lösungsmengen ausrechnen.
LösungDurch Einsetzen der x und y Werte in die Gleichungssysteme können wir überprüfen zu welchem Gleichungssystem die gegebene Lösungsmenge gehört. Nur in
$\begin{align} &\text{I}& -4x+5y&=-55 \\ &\text{II}& -7x+2y&=-49 \\ \end{align}$
erhalten wir eine wahre Aussage:
$\begin{align} &\Rightarrow& &\text{I}& -4x+5y&=-55 \\ &\Rightarrow& &\text{II}& -7x+2y&=-49 \\ &\Rightarrow& &\text{I}& -4(5)+5(-7)&=-55 \\ &\Rightarrow& &\text{II}& -7(5)+2(-7)&=-49 \\ &\Rightarrow& &\text{I}& -20+(-35)&=-55 \\ &\Rightarrow& &\text{II}& -35+(-14)&=-49 \\ &\Rightarrow& &\text{I}& -55 &=-55 \\ &\Rightarrow& &\text{II}& -49&=-49 \\ \end{align}$
Mit der Cramerschen Regel kommen wir ebenfalls auf die gleiche Lösungsmenge:
$B= \begin{pmatrix} -4 & 5 & -55 \\ -7 & 2 & -49 \end{pmatrix}$
Nun bestimmen wir die Determinanten:
$det~A=det \begin{pmatrix} -4 & 5 \\ -7 & 2 \end{pmatrix}=-4 \cdot 2 - 7 \cdot 5=-8 - 35=27$
$det~A_x=det \begin{pmatrix} -55 & 5 \\ -49 & 2 \end{pmatrix}=-55 \cdot 2 - (-49) \cdot 5=-110 + 245=135$
$det~A_y=det \begin{pmatrix} -4 & -55 \\ -7 & -49 \end{pmatrix}=-4 \cdot (-49) - (-7) \cdot (-55)=196 - 385=-189$
Jetzt müssen wir nur noch unsere Werte in die Cramersche Regel einsetzen und wir erhalten die x und y Werte der Lösungsmenge:
$x=\frac{135}{27}=5$
$y=\frac{-189}{27}=-7$
9.711
sofaheld-Level
6.600
vorgefertigte
Vokabeln
8.343
Lernvideos
38.729
Übungen
33.706
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Klassenstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung







 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?




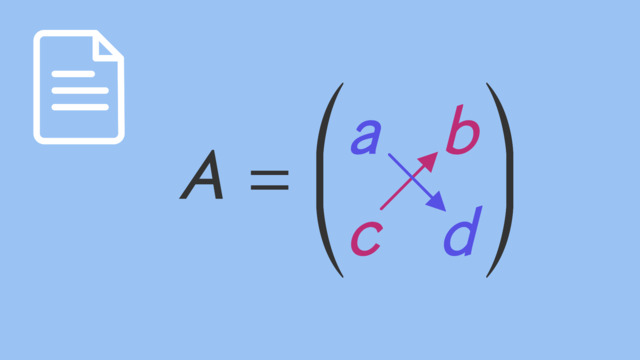









Es war hilfreich aber es ging zu lange
fill zu swer fur die 1ste klase
Sehr hilfreich