Spiegelung, Drehung und Translation
Lineare Abbildungen lassen sich mithilfe von Matrizen darstellen. Dies erfährst du hier am Beispiel verschiedener solcher Abbildungen.
Beliebteste Videos
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
Abbildungen in der Ebene und im Raum
Mit Matrizen kannst du verschiedene Zusammenhänge in der Mathematik beschreiben. Wir betrachten im Folgenden lineare Abbildungen in der Ebene ($\mathbb{R}^{2}$) sowie im Raum ($\mathbb{R}^{3}$). Um von einer linearen Abbildung $f$ sprechen zu können, müssen Bedingungen erfüllt sein. Für Vektoren $\vec x$ sowie $\vec y$ aus dem betreffenden Vektorraum sowie eine Zahl $k\in\mathbb{R}$ muss gelten:
- $f\left(\vec x+\vec y\right)=f\left(\vec x\right)+f\left(\vec y\right)$
- $f\left(k\cdot \vec x\right)=k\cdot f\left(\vec x\right)$
Insbesondere gilt dann:
- Für $f:~\mathbb{R}^{2}~\rightarrow~\mathbb{R}^{2}$ existiert eine $(2\times 2)$-Matrix $A$, sodass $f\left(\vec x\right)=A\cdot \vec x$ ist,
- und für $f:~\mathbb{R}^{3}~\rightarrow~\mathbb{R}^{3}$ existiert eine $(3\times 3)$-Matrix $A$, sodass $f\left(\vec x\right)=A\cdot \vec x$ ist.
Nun schauen wir uns einzelne lineare Abbildungen an. Dabei beschränken wir uns auf Abbildungen $f:~\mathbb{R}^{2}~\rightarrow~\mathbb{R}^{2}$. Die resultierenden Matrizen sehen für den $\mathbb{R}^{3}$ ähnlich aus.
Kongruenzabbildungen
Unter Kongruenzabbildungen versteht man solche Abbildungen, bei denen eine geometrische Figur und deren Bildfigur zueinander kongruent (deckungsgleich) sind.
Spiegelung
Ist es möglich einen Punkt an einer Ebene zu spiegeln? Du kannst Punkte oder andere beliebige geometrische Figuren durch Spiegelung, zum Beispiel an den Koordinatenachsen oder -ebenen in andere Punkte oder geometrische Figuren abbilden. Betrachte den Punkt $P(3|4)$ im zweidimensionalen Koordinatensystem. Durch Spiegelung an der $x$-Achse erhältst du den Bildpunkt $P'(3|{-4})$. Du siehst, die $y$-Koordinate hat nun ein umgekehrtes Vorzeichen. Die zugehörige Spiegelungsmatrix $A$ ist gegeben durch:
$A=\begin{pmatrix} 1&0 \\ 0&-1 \end{pmatrix}$
Drehung
Möchtest du ein geometrisches Element drehen, benötigst du ein Drehzentrum sowie einen Drehwinkel $\alpha$. Auch eine solche Drehung kannst du mithilfe einer Matrix, der sogenannten Drehmatrix, angeben. Im Folgenden sei der Koordinatenursprung das Drehzentrum:
$A=\begin{pmatrix} \cos(\alpha)&-\sin(\alpha) \\ \sin(\alpha)&\cos(\alpha) \end{pmatrix}$
Hier siehst du eine Drehung im zweidimensionalen Koordinatensystem:
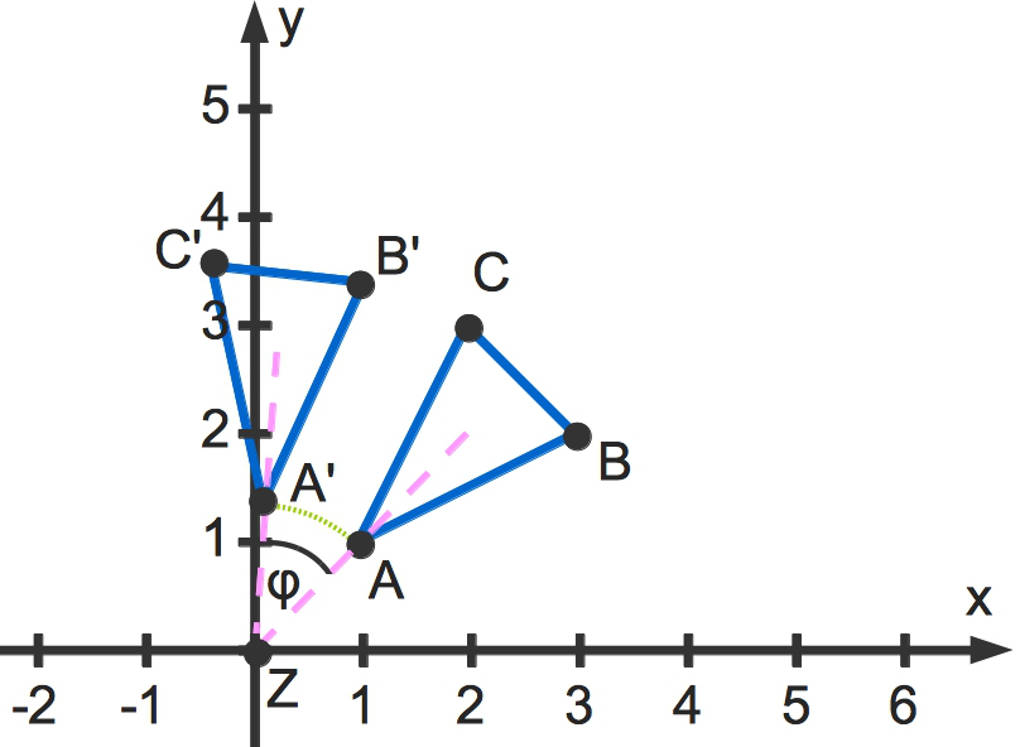
Orthogonale Matrizen
Die oben angegebenen Matrizen sind orthogonale Matrizen: Eine orthogonale Matrix ist eine quadratische Matrix, deren Zeilen- und Spaltenvektoren paarweise orthonormal zueinander sind.
Nun müssen wir natürlich noch klären, was orthonormal bedeutet.
- In diesem Wort steckt zum einen ortho: Das bedeutet, dass die Vektoren paarweise senkrecht zueinander sein müssen.
- Zum anderen kommt normal darin vor: Die Vektoren müssen jeweils normiert sein, das bedeutet, dass sie die Länge $1$ haben.
Jede lineare Abbildung, deren Abbildungsmatrix eine orthogonale Matrix ist, ist eine Kongruenzabbildung.
Eine weitere Kongruenzabbildung ist die Parallelverschiebung.
Weitere lineare Abbildungen
Die nun folgenden linearen Abbildungen sind keine Kongruenzabbildungen.
Zentrische Streckung
Für eine zentrische Streckung benötigst du ein Streckzentrum sowie einen Streckfaktor $k$.
Übrigens: Da bei einer linearen Abbildung insbesondere für den Koordinatenursprung gilt, dass dieser immer auf sich selbst abgebildet wird, ist das Streckzentrum der Koordinatenursprung. Aus diesem Grund ist auch das Drehzentrum bei der Drehung der Koordinatenursprung.
Die zugehörige Matrix sieht dann so aus:
$A=\begin{pmatrix} k&0 \\ 0&k \end{pmatrix}$
Das blaue Viereck $ABCD$ wird gestreckt. So entsteht das grüne Bildviereck $A'B'C'D'$:
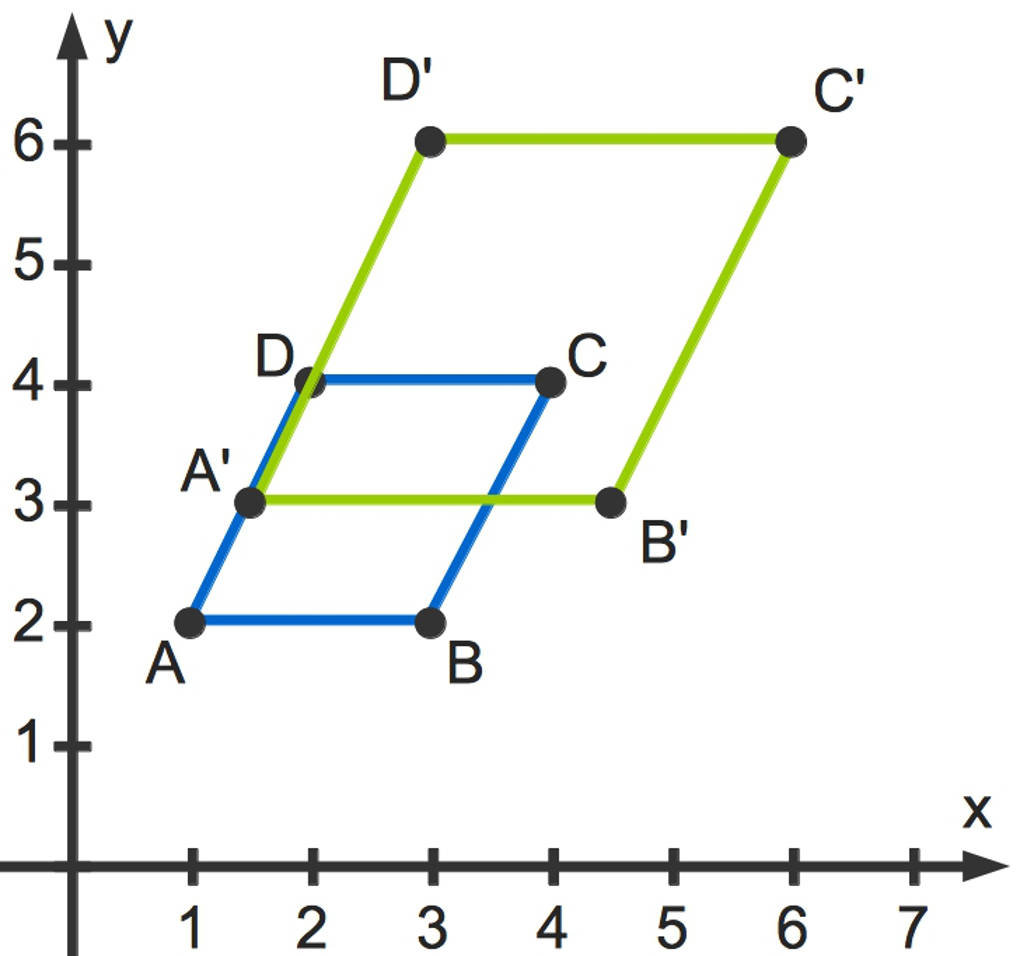
Wenn zum Beispiel $k=-1$ ist, erhältst du die Spiegelung am Koordinatenursprung oder auch eine Drehung um $180^\circ$.
Projektion
Du kannst Projektionen auf Koordinatenachsen oder Koordinatenebenen durchführen. Wenn du den Punkt $P(3|4)$ auf die $x$-Achse projizierst, erhältst du den Bildpunkt $P'(3|0)$.
Dies erreichst du durch die Projektionsmatrix:
$A=\begin{pmatrix} 1&0 \\ 0&0 \end{pmatrix}$
Orthogonale Affinitäten
Zu guter Letzt betrachten wir noch orthogonale Affinitäten: Eine orthogonale Affinität ist eine senkrechte Achsenstreckung. Dabei wird ein Punkt $P(x|y)$ auf $P(x'|y')$ abgebildet. Betrachte zum Beispiel die orthogonale Affinität zur $x$-Achse: $P(3|4)~\rightarrow~P'(3|2\cdot 4)=P'(3|8)$.
Die zugehörige Abbildungsmatrix sieht dann so aus:
$A=\begin{pmatrix} 1&0 \\ 0&2 \end{pmatrix}$ oder allgemein $A=\begin{pmatrix} 1&0 \\ 0&k \end{pmatrix}$
Alle Videos zum Thema
Videos zum Thema
Spiegelung, Drehung und Translation (5 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Spiegelung, Drehung und Translation (5 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung








 Drehung im Koordinatensystem – Anleitung
Drehung im Koordinatensystem – Anleitung
 Zentrische Streckung im Koordinatensystem – Anleitung
Zentrische Streckung im Koordinatensystem – Anleitung
 Lineare Abbildungen durch Matrizen – Abbildungen im Raum
Lineare Abbildungen durch Matrizen – Abbildungen im Raum
 Parallelverschiebung von Polynomen im Koordinatensystem
Parallelverschiebung von Polynomen im Koordinatensystem
 Orthogonale Affinität
Orthogonale Affinität












