Grundlagen zu Potenzen
Potenz, Exponent, Hochzahl, Basis, hoch 0, negativer Exponent, Zehnerpotenzen, wissenschaftliche Schreibweise
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
Was ist eine Potenz?
Anstatt die gleiche Zahl mehrfach zu addieren, kannst du diese Zahl auch mit einem Faktor multiplizieren. Du kannst also abkürzend schreiben:
$\underbrace{5+5+5+5}_{4-\text{mal}}=4\cdot 5$.
Ebenso kannst du Produkte vereinfachen, in denen der gleiche Faktor vorkommt:
$\underbrace{5\cdot 5\cdot 5\cdot 5}_{4-\text{mal}}=5^4$.
Der Term $5^4$ wird als Potenz bezeichnet. Du sagst: „Fünf hoch vier.“
Also ist die Potenzschreibweise eine abkürzende Schreibweise für ein Produkt, in welchem ein Faktor mehrmals vorkommt.
Beispiele
- $\underbrace{2\cdot 2\cdot 2}_{3-\text{mal}}=2^3$
- $\underbrace{3\cdot 3}_{2-\text{mal}}=3^2$
- $\underbrace{16\cdot 16\cdot \dots \cdot 16}_{7-\text{mal}}=16^7$
Eigenschaften und Bezeichnungen
Wir können einige Eigenschaften von Potenzen feststellen:
- Der Faktor, der mehrmals auftaucht, steht in der Potenz unten. Dies ist die Basis.
- Die Häufigkeit, mit welcher dieser Faktor auftritt, steht in der Potenz oben. Dies ist der Exponent.
Hier siehst du die Bezeichnungen für eine allgemeine Potenz $a^n=\underbrace{a\cdot a\cdot ... \cdot a}_{\text{n-mal}}$ im Überblick:
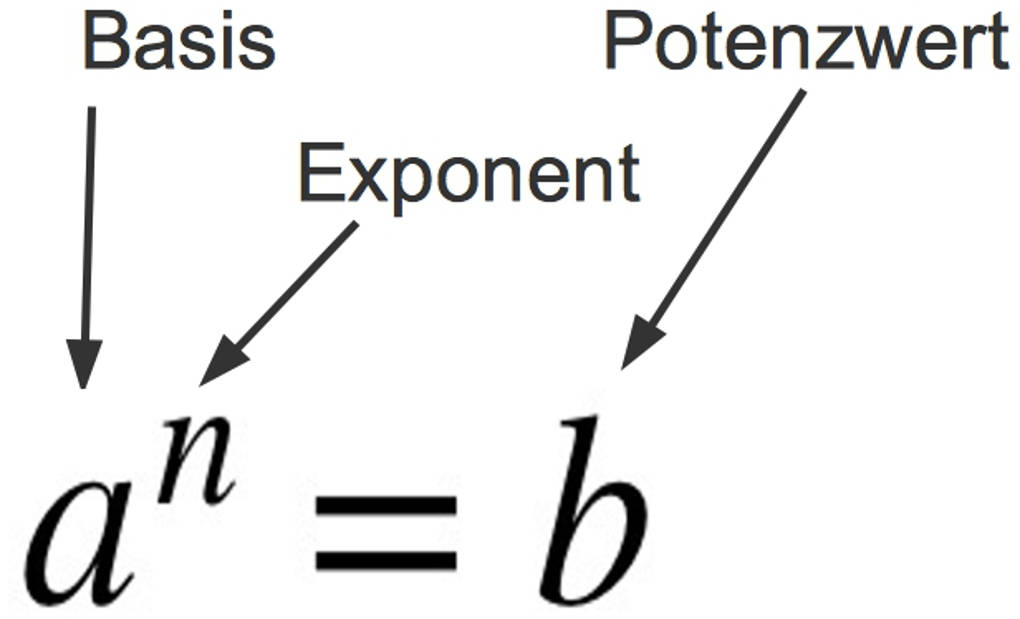
Dabei ist $a\in \mathbb{R}$ und $n\in \mathbb{N}$. $a$ ist also eine beliebige Zahl, der Exponent $n$ ist in der Regel eine natürliche Zahl $1, 2, 3, 4, ...$
Potenzen berechnen
- $5^3=5\cdot 5\cdot 5=25 \cdot 5 = 125$
- $3^4=3\cdot 3\cdot 3\cdot 3=9 \cdot 9=81$
- $2^5=2\cdot 2\cdot 2\cdot 2\cdot 2=4 \cdot 8=32$
Der Exponent $1$
$a^1$ bedeutet, dass der Faktor $a$ in einem Produkt einmal vorkommt. Also ist $a^1=a$ für jede Basis $a\in\mathbb{R}$.
Quadratzahlen
Quadratzahlen sind Zahlen, die sich als Quadrat, also als eine Potenz mit dem Exponenten $2$, schreiben lassen.
$\begin{array}{cccc} 1^2 =1&4^2=16&7^2=49 &10^2=100\\ 2^2=4&5^2=25&8^2=64 &~\\ 3^2=9 &6^2=36 &9^2=81&~ \end{array}$
Wir können zwischen zwei Formulierungen wählen: „... hoch zwei“ oder „... zum Quadrat“.
Kubikzahlen
Kubikzahlen sind Zahlen, die sich als Potenz mit dem Exponenten $3$ ausdrücken lassen:
$\begin{array}{cccc} 1^3&=&1&~&4^3&=&64&~&7^3&=&343&~&10^3&=&1000\\ 2^3&=&8&~&5^3&=&125&~&8^3&=&512&~&~&~&~\\ 3^3&=&27 &~&6^3&=&216&~&9^3&=&729&~&~&~&~ \end{array}$
Zweierpotenzen
Zweierpotenzen sind Potenzen mit der $2$ als Basis.
$\begin{array}{cccc} 2^1=2&2^4=16&2^7=128&2^{10}=1024\\ 2^2=4&2^5=32&2^8=256&~\\ 2^3=8 &2^6=64&2^9=512&~ \end{array}$
Zehnerpotenzen
Im Alltag nutzen wir das Zehnersystem, welches auf den Zehnerpotenzen basiert. Dies sind Potenzen mit der $10$ als Basis.
$\begin{array}{cccc} 10^1&=&10&~&10^4&=&10000&~\\ 10^2&=&100&~&10^5&=&100000&~\\ 10^3&=&1000 &~&10^6&=&1000000&~ \end{array}$
Zehnerpotenzen lassen sich recht leicht berechnen: $10^n$ ist eine $1$ mit $n$ Nullen.
Zahlen als Potenzen schreiben
Wie kannst du umgekehrt Zahlen als Potenzen schreiben?
Schaue dir dies an dem Beispiel $243$ an. Diese Zahl ist mehrfach durch $3$ teilbar.
$\begin{array}{rcl} 243&=&3\cdot 81\\ &=&3\cdot 3\cdot 27\\ &=&3\cdot 3\cdot 3\cdot 9\\ &=&3\cdot 3\cdot 3\cdot 3\cdot 3\\ &=&3^5 \end{array} $
Potenzieren von Summen und Differenzen
Beim Potenzieren von Summen oder Differenzen gehst du wie folgt vor.
$\begin{array}{rcl} (2x+3)^2&=&(2x+3)\cdot (2x+3)\\ &=&(2x)\cdot (2x)+(2x)\cdot 3+3\cdot (2x)+3\cdot 3\\ &=&4x^2+6x+6x+9\\ &=&4x^2+12x+9 \end{array}$
Ebenso kannst du auch Differenzen potenzieren.
$\begin{array}{rcl} (4-y)^2&=&(4-y)\cdot (4-y)\\ &=&4\cdot 4-4\cdot y-y\cdot 4+y\cdot y\\ &=&16-4y-4y+y^2\\ &=&16-8y+y^2 \end{array}$
Eine Verallgemeinerung davon sind die binomischen Formeln,
- die erste binomische Formel $(a+b)^2=a^2+2ab+b^2$ sowie
- die zweite binomische Formel $(a-b)^2=a^2-2ab+b^2$.
Beachte unbedingt, dass du nicht einfach die einzelnen Summanden quadrieren kannst.
Alle Videos zum Thema
Videos zum Thema
Grundlagen zu Potenzen (5 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Grundlagen zu Potenzen (5 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung







 Potenzen
Potenzen
 Potenzen Definition
Potenzen Definition
 Quadrat- und Kubikzahlen
Quadrat- und Kubikzahlen
 Potenzen – Produkte gleicher Faktoren
Potenzen – Produkte gleicher Faktoren
 Null als Exponent
Null als Exponent









