Ziehen mit/ohne Zurücklegen, mit/ohne Reihenfolge

Inhaltsverzeichnis zum Thema

• Was ist die Kombinatorik?
• Ziehen mit Zurücklegen
• mit Beachtung der Reihenfolge
• ohne Beachtung der Reihenfolge
• Ziehen ohne Zurücklegen
• mit Beachtung der Reihenfolge
• ohne Beachtung Reihenfolge

Was ist die Kombinatorik?

Ein Teilgebiet der Stochastik ist die Kombinatorik. Hier geht es darum, die Möglichkeiten mehrstufiger Zufallsversuche zu zählen.

Sehr anschaulich lässt sich das am Urnenmodell erklären:

In einer Urne befinden sich mehrere Kugeln, die nacheinander gezogen werden. Dabei macht es einen entscheidenden Unterschied, wie man dieses Experiment durchführt. Wird die Reihenfolge gezogener Kugeln beachtet? Legt man eine gezogene Kugel wieder in die Urne zurück?

Man kann mit einem Urnenmodell insgesamt vier verschiedene Experimente durchführen, die wir im Folgenden genauer betrachten.

Ziehen mit Zurücklegen

Wenn nach jedem Ziehen die gezogene Kugel wieder zurückgelegt wird, ändert sich die Anzahl der Kugeln in der Urne nicht.

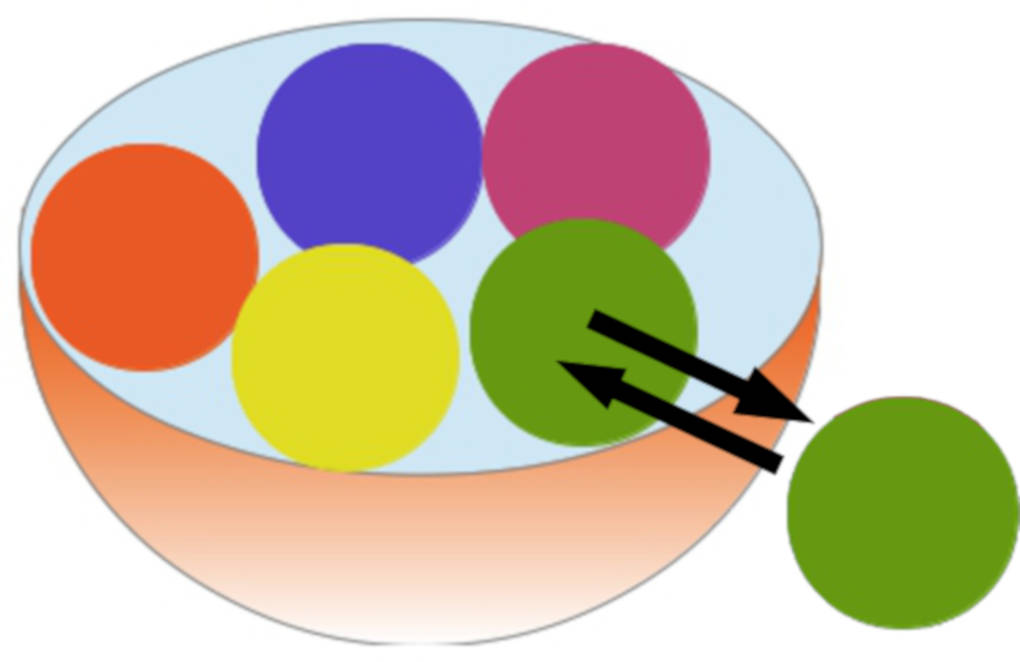
Die grüne Kugel wird in die Urne zurückgelegt. Sie kann im nächsten Durchgang wieder gezogen werden.

mit Beachtung der Reihenfolge

Wir betrachten das oben abgebildete Urnenmodell. In unserer Urne befinden sich also eine grüne, eine blaue, eine gelbe, eine orange und eine violette Kugel. Aus dieser Urne mit fünf Kugeln werden jeweils vier Kugeln mit Zurücklegen und mit Beachtung der Reihenfolge gezogen. Dieses Experiment wird dreimal durchgeführt. Jeder Durchgang entspricht im folgenden Bild einer Reihe mit je vier Kugeln:

Jede Kugel wird für sich betrachtet und gezählt. So liefert jeder der drei Versuchsausgänge ein neues Ergebnis. Hier sehen wir also drei verschiedene Möglichkeiten für den Ausgang dieses Experimentes.

Doch wie viele Möglichkeiten gibt es insgesamt, aus einer Urne mit fünf Kugeln vier Kugeln mit Zurücklegen und mit Beachtung der Reihenfolge zu ziehen? Die Anzahl möglicher Kombinationen für einen solchen Fall erhalten wir über folgende Beziehung:

$n^{k}$

Dabei ist $n$ die Anzahl aller Elemente, die zur Auswahl stehen, und $k$ die Anzahl gezogener Elemente. Wir ziehe also $k$ Elemente aus einer Menge mit $n$ Elementen. Für unser Experiment erhalten wir dann mit $n=5$ und $k=4$ folgende Anzahl möglicher Kombinationen:

$5^{4}=5\cdot5\cdot5\cdot5 =625$

Anwendungsbeispiel:

Bei einem vierstelligen Handycode stehen für jede Stelle jeweils zehn Ziffern, nämlich von $0$ bis $9$, zur Verfügung.

Vergleicht man den vierstelligen Code mit der Anzahl der zu ziehenden Kugeln ($k$) und die zehn möglichen Ziffern mit den Kugeln insgesamt ($n$), erhält man $10^{4} = 10000$ Möglichkeiten.

ohne Beachtung der Reihenfolge

Nun ziehen wir aus dem gleichen Urnenmodell wieder vier Kugeln. Die gezogene Kugel wird wieder nach jedem Zug in die Urne zurückgelegt. Diesmal spielt die Reihenfolge, in der die Kugeln gezogen werden, allerdings keine Rolle. Nach dreimaligem Durchführen dieses Experimentes erhalten wir wieder das im Folgenden abgebildete Ergebnis:

Da die Reihenfolge der gezogenen Kugeln nicht beachtet wird, geht es grundsätzlich darum, wie viele Kugeln von welcher Farbe gezogen wurden. Somit zählen die ersten beiden Durchgänge als eine Möglichkeit. In beiden wurden nämlich zwei violette, eine grüne und eine blaue Kugel gezogen. Insgesamt sehen wir hier also nur zwei unterschiedliche Kombinationen.

Beim Ziehen mit Zurücklegen und ohne Beachtung der Reihenfolge gibt es weniger Möglichkeiten als beim Ziehen mit Zurücklegen und mit Beachtung der Reihenfolge.

Wie viele Möglichkeiten gibt es insgesamt, aus einer Urne mit fünf Kugeln vier Kugeln mit Zurücklegen und ohne Beachtung der Reihenfolge zu ziehen?

Allgemein gilt für das Ziehen mit Zurücklegen und ohne Beachtung der Reihenfolge folgende Beziehung:

$\binom{n+k-1}{k} = \frac{(n+k-1)!}{k!(n-1)!}$

Den Ausdruck auf der linken Seite der obigen Gleichung nennt man Binomialkoeffizient und spricht „$n+k-1$ über $k$“. Bei insgesamt $n=5$ Kugeln und $k=4$ zu ziehenden Kugeln erhält man für diesen Fall folgende Anzahl möglicher Kombinationen:

$\binom{5+4-1}{4}=\frac{(5+4-1)!}{4! (5-1)!}$=$\frac{8!}{4!4!}$=$\frac{40320}{576}=70$

Anwendungsbeispiel:

Wie viele Kombinationsmöglichkeiten gibt es beim dreimaligen Würfeln?

Vergleicht man die drei Würfe mit der Anzahl der zu ziehenden Kugeln ($k$) und die sechs möglichen Ergebnisse, nämlich die Würfelaugen $1$ bis $6$, mit der Gesamtzahl der Kugeln ($n$), erhält man folgende Anzahl möglicher Ergebnisse:

$\binom{6+3-1}{3} =\frac{(6+3-1)!}{3! (6-1)!} = \frac{8!}{(3! 5!)} = 56$

Ziehen ohne Zurücklegen

Nun wird die gezogene Kugel nicht mehr zurückgelegt. Also gibt es nach jedem Zug eine Kugel weniger in der Urne. Je nachdem, wie viele Kugeln aus der Urne gezogen werden, kann es auch mal sein, dass am Ende keine Kugeln mehr übrig sind.

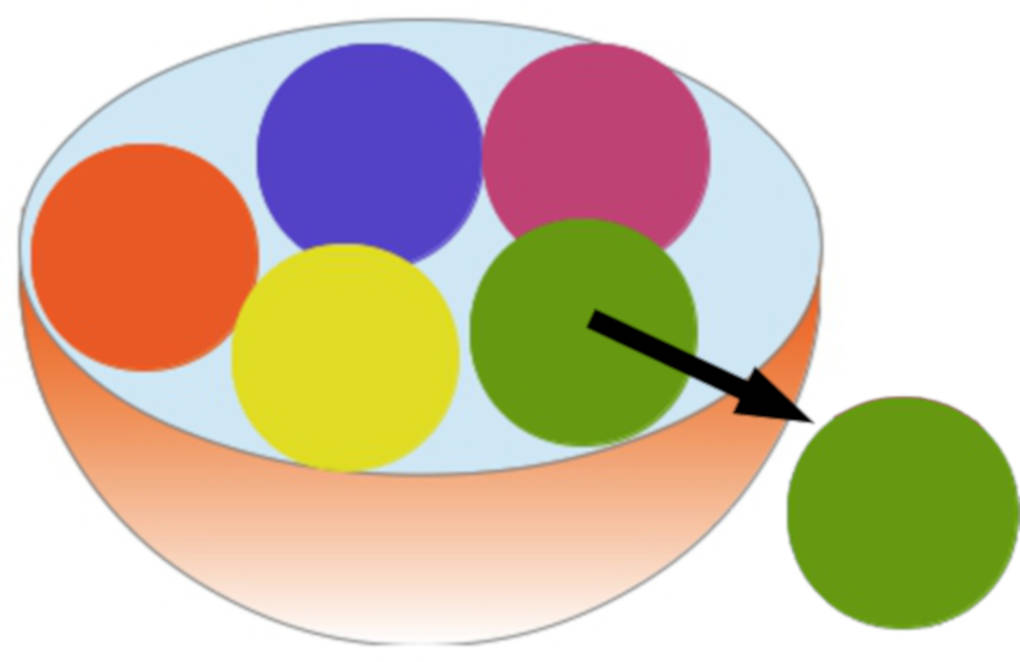
Die grüne Kugel wird gezogen und nicht wieder in die Urne zurückgelegt.

mit Beachtung der Reihenfolge

Wir betrachten wieder das oben abgebildete Urnenmodell. Aus dieser Urne mit fünf Kugeln werden in drei Durchgängen jeweils vier Kugeln ohne Zurücklegen und mit Beachtung der Reihenfolge gezogen. Die Ergebnisse der einzelnen Durchgänge sind im folgenden Bild je in einer Reihe aufgeführt:

Die vier Kugeln werden nacheinander aus der Urne gezogen, in jedem Durchgang in einer anderen Reihenfolge. Da nun die Reihenfolge beachtet wird, zählt jeder Durchgang als ein Ergebnis. Wir sehen hier also drei Möglichkeiten für den Ausgang dieses Zufallsexperimentes.

Wie viele Möglichkeiten gibt es insgesamt, aus einer Urne mit fünf Kugeln vier Kugeln ohne Zurücklegen und mit Beachtung der Reihenfolge zu ziehen? Die Anzahl möglicher Kombinationen für einen solchen Fall der Kombinatorik erhalten wir über folgende Beziehung:

$\frac{n!}{(n-k)!}$

Bei insgesamt $n=5$ Kugeln und $k=4$ zu ziehenden Kugeln erhalten wir also folgende Anzahl für die Möglichkeiten:

$\frac{5!}{(5-4)!}=5\cdot3\cdot2 = 120$

Anwendungsbeispiel:

Bei der Fußball-Europameisterschaft stehen acht Mannschaften im Viertelfinale, von denen drei eine Medaille gewinnen werden. Wie viele Möglichkeiten gibt es dafür? Vergleicht man die drei Medaillen mit der Anzahl der zu ziehenden Kugeln ($k$) und die acht Mannschaften mit der Gesamtzahl der Kugeln ($n$), erhält man folgende Anzahl für die Möglichkeiten:

$\frac{8!}{(8-3)!}= \frac{8!}{5!}= 8\cdot7\cdot6 = 336$

ohne Beachtung Reihenfolge

Wieder ziehen wir aus dem betrachteten Urnenmodell vier Kugeln ohne Zurücklegen. Diesmal spielt die Reihenfolge, in der die Kugeln gezogen werden, keine Rolle.

Achtet man bei den obigen drei Versuchsausgängen nicht auf die Reihenfolge der Kugeln, liefern die ersten beiden Durchgänge nur ein Ergebnis, nämlich eine Kombination aus einer gelben, einer grünen, einer blauen und einer orangefarbenen Kugel. Insgesamt sehen wir hier also nur zwei mögliche Ergebnisse.

Beim Ziehen ohne Zurücklegen und ohne Beachtung der Reihenfolge gibt es weniger Möglichkeiten als beim Ziehen ohne Zurücklegen und mit Beachtung der Reihenfolge.

Wie viele Möglichkeiten gibt es insgesamt, aus einer Urne mit fünf Kugeln vier Kugeln ohne Zurücklegen und ohne Beachtung der Reihenfolge zu ziehen?

Allgemein gilt für das Ziehen ohne Zurücklegen und ohne Beachtung der Reihenfolge folgende Beziehung:

$\binom{n}{k} = \frac{n!}{k!(n-k)!}$

Bei einer Gesamtzahl von $n=5$ Kugeln und $k=4$ Zügen erhält man dann:

$\binom{5}{4} = \frac{5!}{4! (5-4)!} = \frac{5!}{4!1!}= \frac{120}{24}= 5$

Anwendungsbeispiel:

Wie viele Möglichkeiten gibt es bei der Ziehung der Lottozahlen ($6$ aus $49$)? Vergleicht man die sechs ausgewählten Zahlen mit der Anzahl der zu ziehenden Kugeln ($k$) und die $49$ Zahlen mit der Gesamtzahl der Kugeln ($n$), erhält man folgende Anzahl für die Kombinationsmöglichkeiten:

$\binom{49}{6}= \frac{49!}{6!(49-6)!} = \frac{49!}{6!43!} = 13983816$