Bedingte Wahrscheinlichkeit
bedingte Wahrscheinlichkeit, stochastisch unabhängig, Randwahrscheinlichkeit, A unter B, B unter A, Vierfeldertafel, Baumdiagramme rückwärts, totale Wahrscheinlichkeit, Satz von Bayes
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
Was ist eine bedingte Wahrscheinlichkeit?
Schaue dir folgendes Beispiel an.
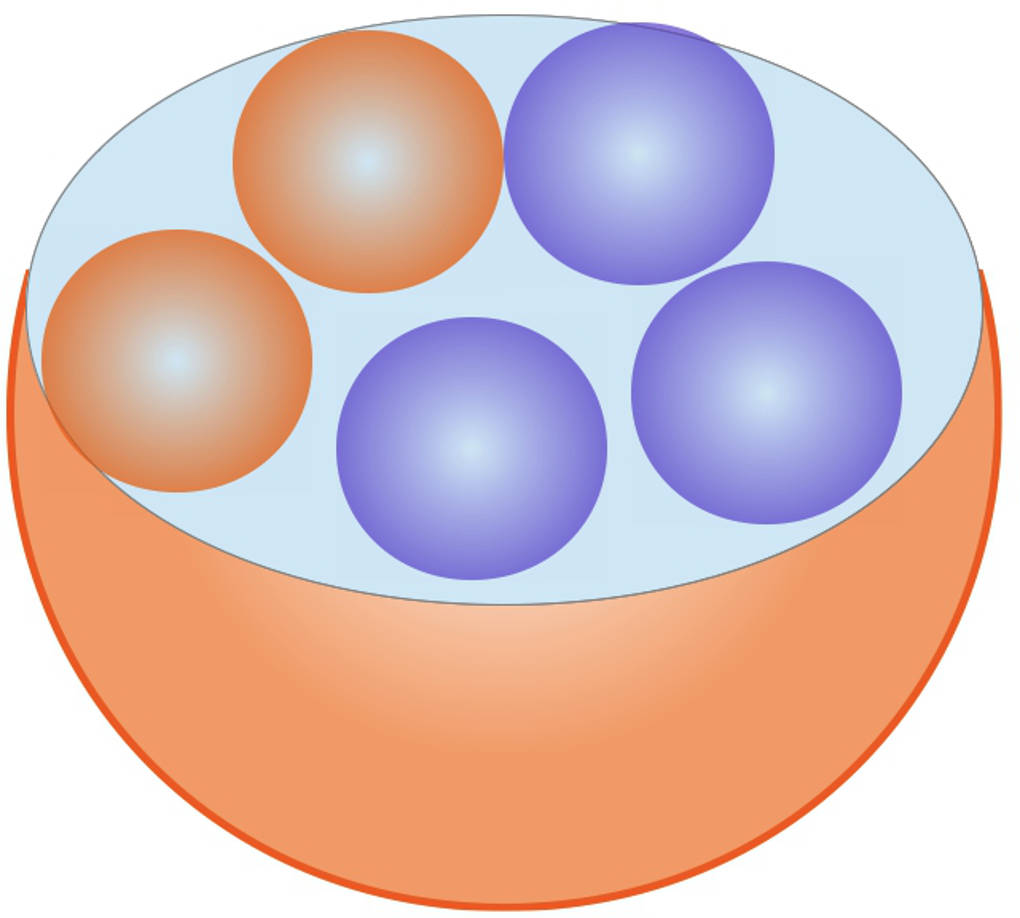
In einer Urne befinden sich fünf Kugeln, davon sind drei blau und zwei rot. Wenn du zwei Kugeln aus dieser Urne ohne Zurücklegen ziehst, kannst du die Wahrscheinlichkeiten in einem Baumdiagramm darstellen:
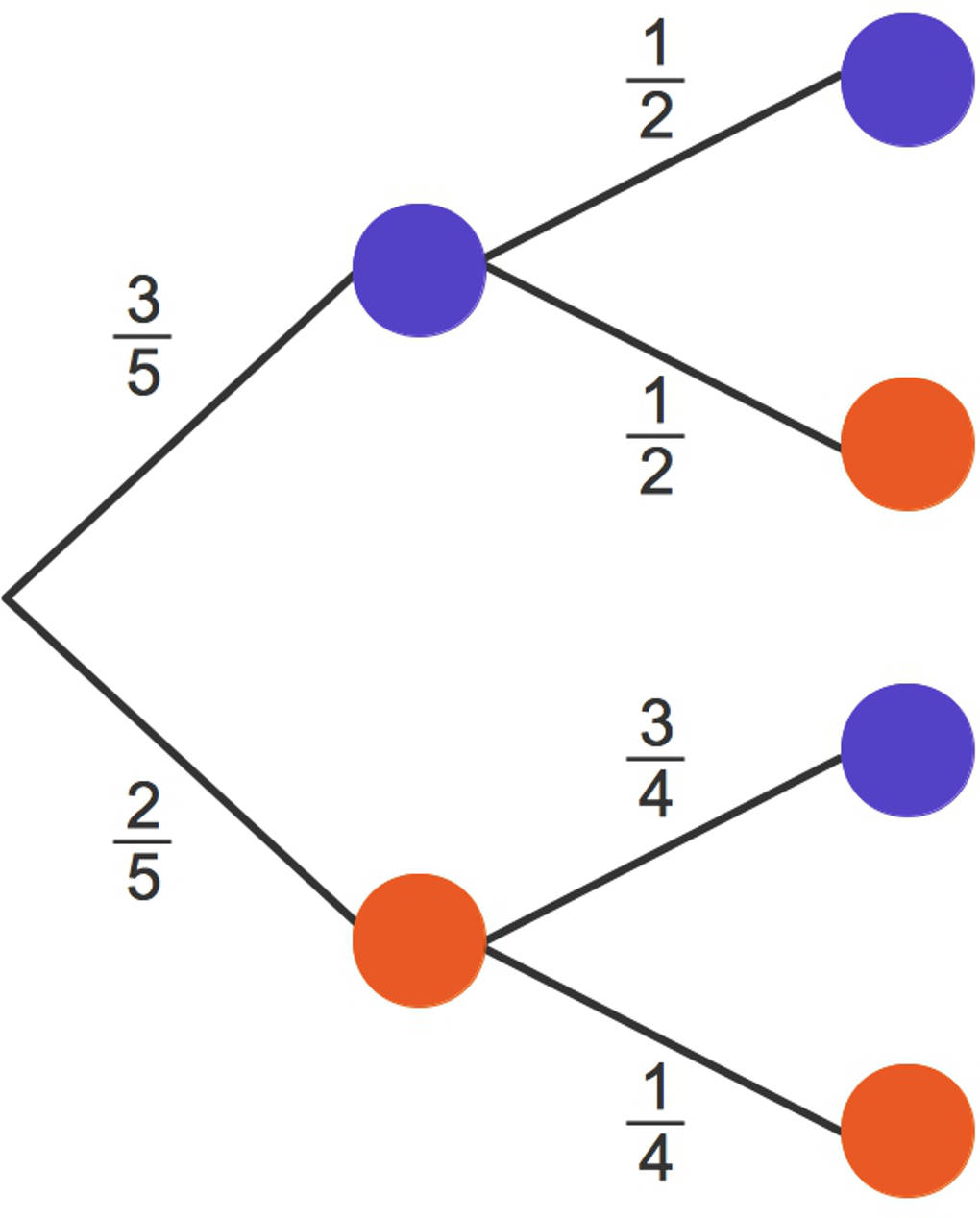
Du kannst an diesem Baumdiagramm erkennen, dass die Wahrscheinlichkeit beim zweiten Zug eine blaue (oder rote) Kugel zu ziehen, davon abhängt, welche Kugel du beim ersten Zug gezogen hast:
- Wenn du beim ersten Zug eine blaue Kugel gezogen hast, dann ist die Wahrscheinlichkeit, beim zweiten Zug eine blaue Kugel zu ziehen $\frac24=\frac12$.
- Hast du beim ersten Zug eine rote Kugel gezogen, so ist die Wahrscheinlichkeit für eine blaue Kugel beim zweiten Zug $\frac34$.
Dies liegt daran, dass die Kugel nicht zurückgelegt wird. Das bedeutet, dass sich die Anzahl der blauen Kugeln und somit deren Anteil ändert in Abhängigkeit von der gezogenen Kugel beim ersten Zug.
Eine solche Wahrscheinlichkeit wird als bedingte Wahrscheinlichkeit bezeichnet.
Bezeichnungen
Schaue dir dieses Baumdiagramm an: Es wird ein zweistufiges Zufallsexperiment betrachtet. Im ersten Durchgang kann das Ereignis $A$ oder dessen Gegenereignis $\bar{A}$ eintreten. Im zweiten Durchgang kann das Ereignis $B$ oder dessen Gegenereignis $\bar{B}$ eintreten.
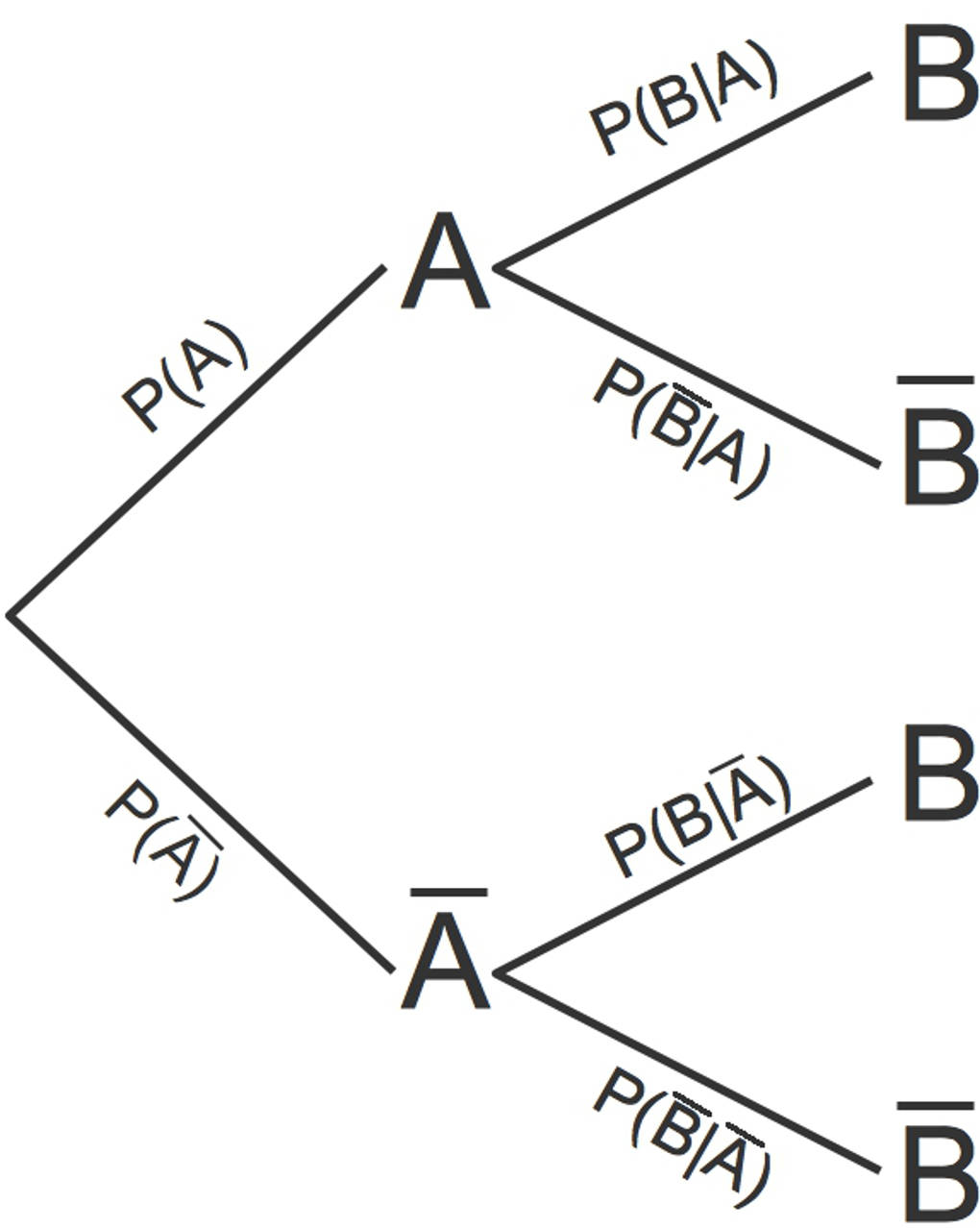
Das Ereignis $B$ (oder auch $\bar{B}$) kann mit verschiedenen Wahrscheinlichkeiten unter der Bedingung des Eintretens eines Ereignisses im ersten Durchgang auftreten.
- $P(B|A)$ ist die Wahrscheinlichkeit für das Eintreten von Ereignis $B$ und der Bedingung, dass das Ereignis $A$ bereits eingetreten ist.
- $P(\bar{B}|A)$ ist die Wahrscheinlichkeit für das Eintreten von Ereignis $\bar{B}$ und der Bedingung, dass das Ereignis $A$ bereits eingetreten ist.
- ...
Rechnen mit bedingten Wahrscheinlichkeiten

Am Ende des oberen Pfades steht das Ereignis: „Es ist sowohl $A$ als auch $B$“ eingetreten, also $A\cap B$.
Der Multiplikationssatz
Mit der Produktregel oder auch 1. Pfadregel kann die Wahrscheinlichkeit des Ereignisses $A\cap B$ wie folgt berechnet werden:
Wir definieren (daher "$:=$" statt nur "$=$"):
$\quad~~~P(A\cap B):=P(A)\cdot P(B|A)$.
Diese Formel kann nach der bedingten Wahrscheinlichkeit $P(B|A)$ umgestellt werden:
$\quad~~~P(B|A)=\frac{P(A\cap B)}{P(A)}$.
Der Satz von der totalen Wahrscheinlichkeit
Das Ereignis $B$ tritt einmal unter der Bedingung von $A$ und einmal unter der Bedingung von $\bar{A}$ ein. Mit der Summenregel oder auch 2. Pfadregel kann die Wahrscheinlichkeit für das Eintreten von $B$ so berechnet werden:
$\quad~~~P(B)=P(A)\cdot P(B|A)+P(\bar{A})\cdot P(B|\bar{A})$.
Der Satz von Bayes
Wenn du das obige Baumdiagramm umkehrst, erhältst du
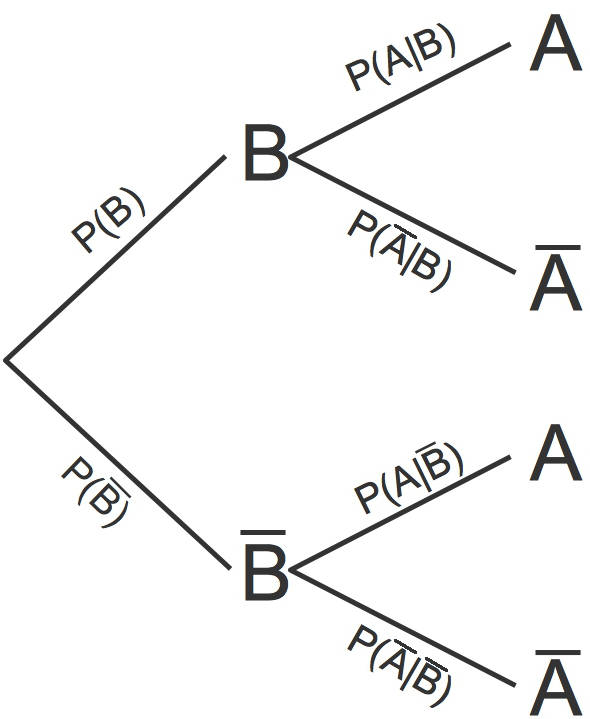
Wie können nun die bedingten Wahrscheinlichkeiten von $A$ (oder $\bar{A}$)unter der Bedingung von $B$ oder $\bar{B}$ berechnet werden?
Du kannst den Multiplikationssatz verwenden. Es gilt
$\quad~~~P(A\cap B)=P(B\cap A)=P(B)\cdot P(A|B)$,
oder, nach $P(A|B)$ umgeformt:
$\quad~~~P(A|B)=\frac{P(A\cap B)}{P(B)}$.
Nun setzt du die Wahrscheinlichkeiten für $P(A\cap B)$ aus dem Multiplikationssatz sowie die für $P(B)$ aus dem Satz von der totalen Wahrscheinlichkeit ein:
$\quad~~~P(A|B)=\frac{P(A)\cdot P(B|A)}{P(A)\cdot P(B|A)+P(\bar{A})\cdot P(B|\bar{A})}$.
Dies ist die Aussage des Satzes von Bayes.
Beispielaufgabe
Da das nun sehr viel Theorie war, schauen wir uns eine Beispielaufgabe an, um die obigen Aussagen zu üben.
Es ist bekannt, dass $12\%$ der Bewohner eines Landes einen Schnupfenvirus haben. Es wird ein Test durchgeführt,
- der in $85\%$ der Fälle, in denen das Virus vorliegt, dieses auch anzeigt und
- in $20\%$ der Fälle, in denen das Virus nicht vorliegt, dieses fälschlicherweise anzeigt.
Du kannst nun das folgende Baumdiagramm erstellen. Dabei steht
- $V$ für „Eine Person ist vom Virus befallen.“ und
- $T$ für „Der Test zeigt den Virus an.“
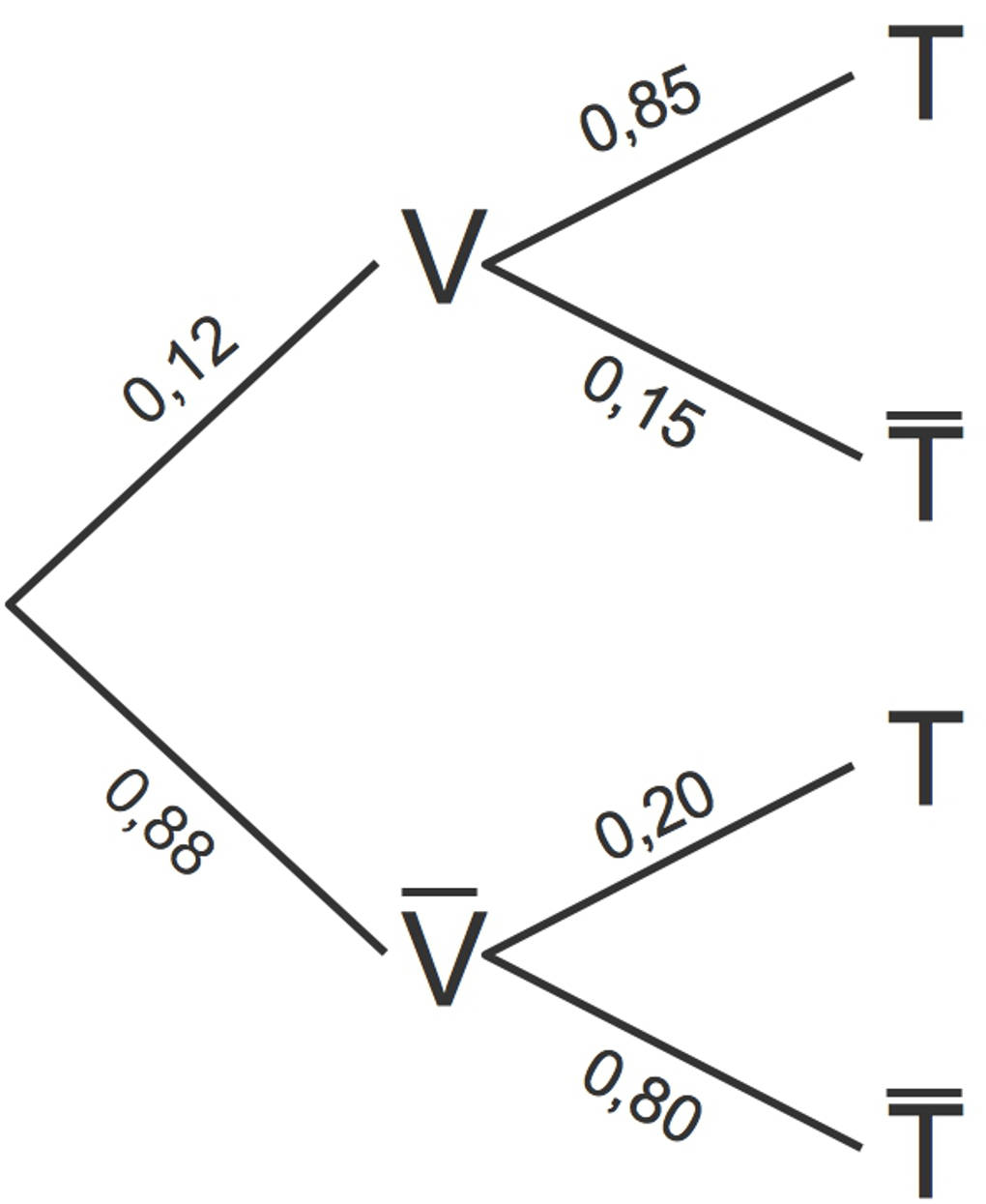
Zum Beispiel ist die bedingte Wahrscheinlichkeit dafür, dass der Test einen Virus anzeigt, wenn dieser auch tatsächlich vorliegt $P(T|V)=0,85$.
Wie groß ist die Wahrscheinlichkeit, dass jemand von dem Virus befallen ist und dieses auch durch den Test angezeigt wird?
Du wendest den Multiplikationssatz an. Gesucht ist hier die Wahrscheinlichkeit:
$\quad~~~P(V\cap T)=0,12\cdot0,85=0,102$.
Wie groß ist die Wahrscheinlichkeit, dass der Test das Virus anzeigt?
Dieses Mal ist nach $P(T)$ gefragt, unabhängig davon ob tatsächlich das Virus vorliegt oder nicht. Diese Wahrscheinlichkeit berechnest du mit dem Satz von der totalen Wahrscheinlichkeit:
$\quad~~~P(T)=0,12\cdot0,85+0,88\cdot 0,2=0,278$.
Wie groß ist die Wahrscheinlichkeit, dass eine Person, bei welcher der Test das Virus anzeigt, tatsächlich von diesem Virus befallen ist?
Dieses Mal ist eine bedingte Wahrscheinlichkeit $P(V|T)$ gesucht. Du kannst die bereits berechneten Wahrscheinlichkeiten verwenden. Dies entspricht dem Satz von Bayes:
$\quad~~~P(V|T)=\frac{P(V\cap T)}{P(V)}=\frac{0,102}{0,278}\approx0,367$.
Das bedeutet, dass eine Person, die ein positives Testergebnis hat, mit einer Wahrscheinlichkeit von ungefähr $37\%$ tatsächlich von diesem Virus befallen ist.
Alle Videos zum Thema
Videos zum Thema
Bedingte Wahrscheinlichkeit (3 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Bedingte Wahrscheinlichkeit (3 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung





 Bedingte Wahrscheinlichkeit – Einführung
Bedingte Wahrscheinlichkeit – Einführung
 Bedingte Wahrscheinlichkeit – Baumdiagramm und Vierfeldertafel
Bedingte Wahrscheinlichkeit – Baumdiagramm und Vierfeldertafel
 Bedingte Wahrscheinlichkeit – Übungen
Bedingte Wahrscheinlichkeit – Übungen









