Quadratische Funktionen: Normalparabel, Streckung, Stauchung und Verschiebung
Eine quadratische Funktion hat als höchsten Exponenten eine zwei. Daher kommt der Name, vom Quadrieren. Der Funktionsgraph einer quadratischen Funktion ist eine Parabel.
Beliebteste Videos
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Was ist eine quadratische Funktion?
- Die Bedeutung des Parameters $a$
- Die Bedeutung des Parameters $c$
- Die quadratische Funktion der Form $f(x)=(x+d) ^2$
- Die Bedeutung des Parameters $d$
Was ist eine quadratische Funktion?
Ganz allgemein sieht eine quadratische Funktion $f$ so aus: $f(x)=ax^{2}+bx+c$. Dabei sind $a\neq 0,~b,~c\in\mathbb{R}$ Parameter.
Du siehst, die Potenz mit dem höchsten Exponenten ist $x^{2}$, also $x$ zum Quadrat. Daher kommt auch der Name. Der Funktionsgraph einer quadratischen Funktion ist eine Parabel. Hier siehst du die Normalparabel zu der quadratischen Funktion $f$ mit $f(x)=x^{2}$.
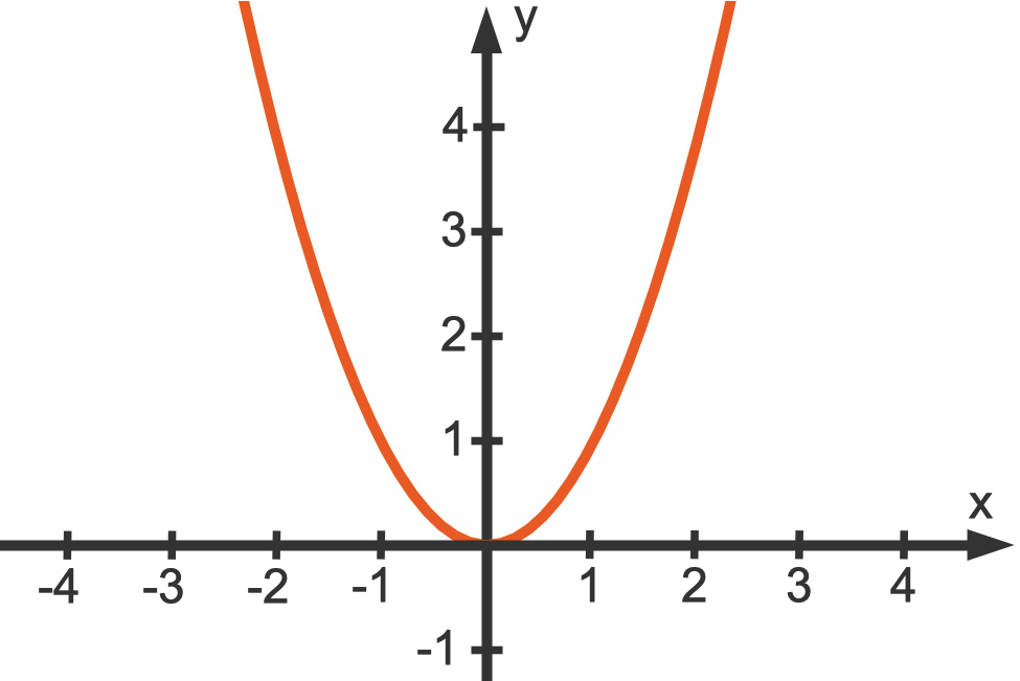
Du lernst im Folgenden, welche Auswirkungen die Parameter auf die Parabel haben. Dabei ist für die Betrachtung der Parameter $a$ sowie $c$ immer $b=0$.
Die Bedeutung des Parameters $a$
Für $c=0$ schauen wir uns nun die Bedeutung des Parameters $a$ an. Erstelle dir eine Wertetabelle der Funktion $f$ mit $f(x)=a x^{2}$ für $a=1$ (zweite Zeile), $a=4$ (dritte Zeile) sowie $a=\frac14$ (vierte Zeile).
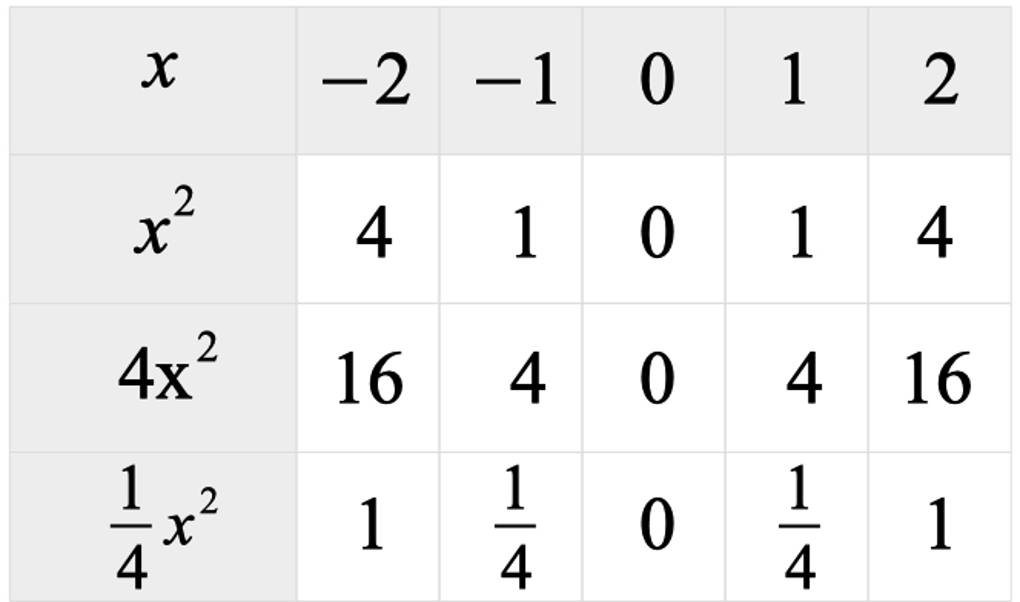
Nun kannst du die so erhaltenen Paare $(x|y)$ in ein Koordinatensystem eintragen. Du erhältst drei Parabeln.
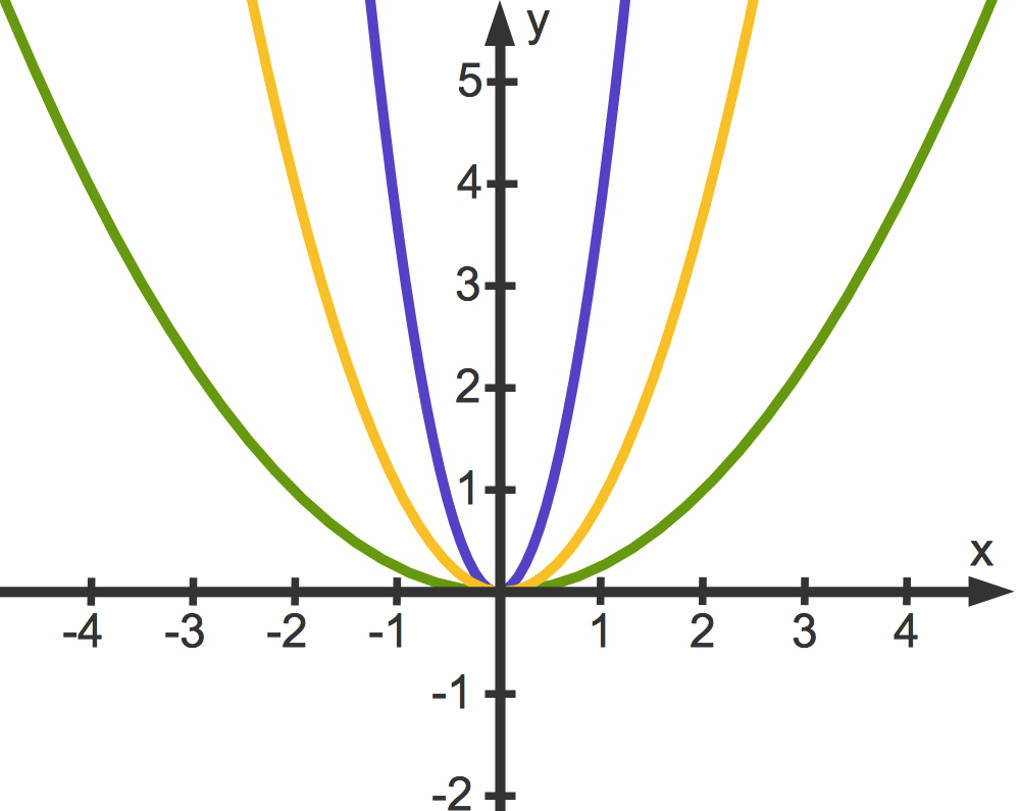
- Die gelbe Parabel gehört zu $x^{2}$,
- die blaue zu $4x^{2}$ und
- die grüne zu $\frac14 x^{2}$.
Fällt dir etwas auf? Betrachte einmal die blaue beziehungsweise die grüne in Relation zu der gelben Normalparabel:
- Die blaue Parabel verläuft enger als die Normalparabel. Man sagt auch, sie ist entlang der $y$-Achse gestreckt.
- Die grüne Parabel verläuft weiter als die Normalparabel. Man sagt auch, sie ist entlang der $y$-Achse gestaucht.
Wenn du übrigens einen negativen Wert für $a$ wählst, erhältst du eine nach unten geöffnete Parabel.
Der Parameter $a$ wird als Streckfaktor bezeichnet.
Du kannst anhand dieses Parameters erkennen, ob die Parabel nach oben oder nach unten geöffnet ist und wie weit sie geöffnet ist:
Für $a>1$ erhältst du eine gestreckte und nach oben geöffnete Parabel.
Für $a=1$ erhältst du die nach oben geöffnete Normalparabel.
Für $0 < a < 1$ erhältst du eine gestauchte und nach oben geöffnete Parabel.
Für $-1 < a < 0$ erhältst du eine gestauchte und nach unten geöffnete Parabel.
Für $a=-1$ erhältst du eine an der $x$-Achse gespiegelte, also nach unten geöffnete, Normalparabel.
Für $a<-1$ erhältst du eine gestreckte und nach unten geöffnete Parabel.
Die Bedeutung des Parameters $c$
Betrachte die Funktion $f$ mit $f(x)=x^{2}+c$. Erstelle für verschiedene Werte von $c$ eine Wertetabelle.
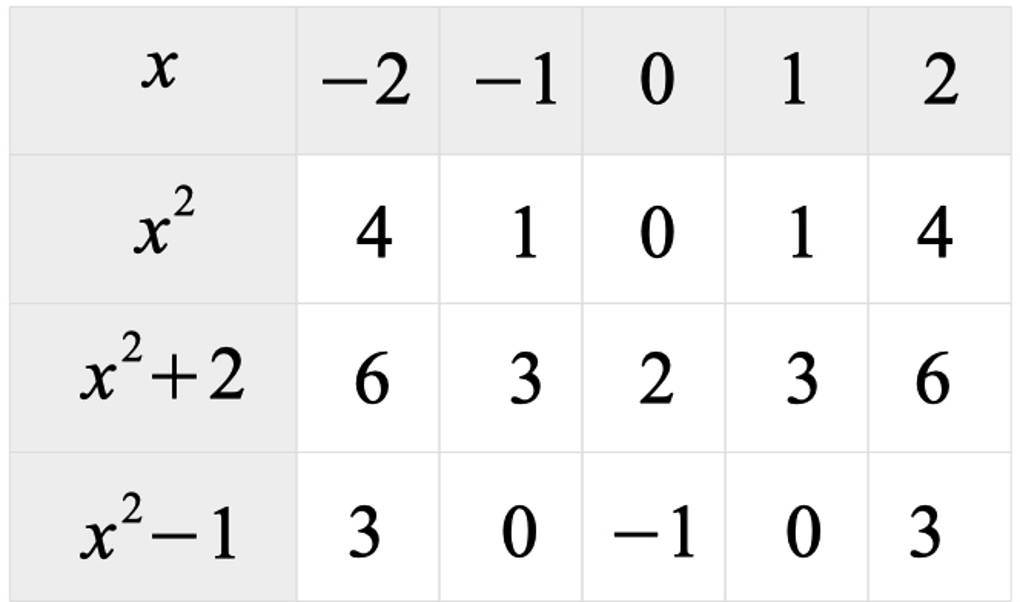
Übertrage die so erhaltenen $(x|y)$-Paare in ein Koordinatensystem. So kommst du zu den folgenden Funktionsgraphen der quadratischen Funktion $f$ mit $f(x)=x^{2}+c$.
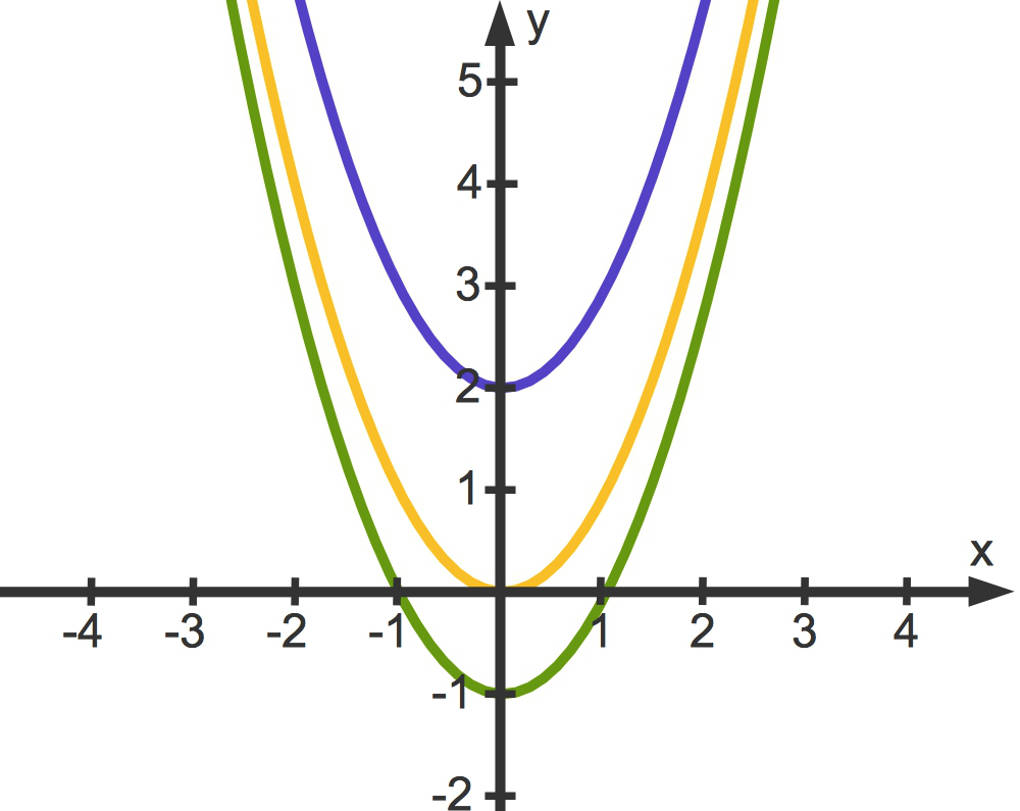
- Die gelbe Parabel gehört zu $x^{2}$,
- die blaue zu $x^{2}+2$ und
- die grüne zu $x^{2}-1$.
Du siehst, dass die Veränderung des Parameters $c$ zu einer Parallelverschiebung der Parabel entlang der $y$-Achse führt:
- Für $c\gt 0$ erhältst du eine Verschiebung nach oben wie bei $f(x)=x^{2}+2$ und
- für $c\lt 0$ eine Verschiebung nach unten wie bei $f(x)=x^{2}-1$.
Du kannst auch die Parameter kombinieren: So erhältst du gestreckte (oder gestauchte) und entlang der $y$-Achse verschobene Parabeln. Dabei ist die $x$-Koordinate des Scheitelpunktes immer $x_{S}=0$ und die $y$-Koordinate $y_{S}=c$.
Die quadratische Funktion der Form $f(x)=(x+d) ^2$
Da hat sich noch ein $d$ ins Quadrat geschlichen! Dieser wird auch Parameter genannt und ist ein Platzhalter für eine ganz normale Zahl. So eine Funktionsgleichung könnte zum Beispiel beschreiben, was mit der Fläche eines Quadrates passiert, wenn beide Seitenlängen $x$ um $d$ verlängert werden. Genauso könnte sie eine Verkürzung der Seitenlängen beschreiben, wenn $d$ negativ ist.
Die Bedeutung des Parameters $d$
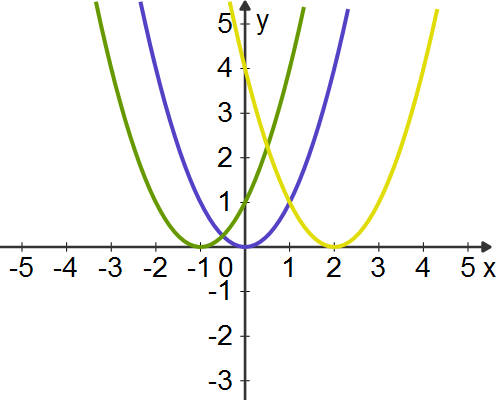
Der Parameter $d$ verschiebt den Scheitelpunkt und damit die ganze Parabel nur auf der $x$-Achse. Aber warum ist das so? Sieh dir dafür folgendes Beispiel an:
$y=(x-2)^2$
Die rechte Seite ist immer positiv, weil alle Zahlen im Quadrat positiv sind. Der kleinste $y$-Wert ist damit null und gleichzeitig die $y$-Koordinate des Scheitelpunkts. Wenn $y=0$ ist, dann muss $x=2$ sein. Weil dann die Klammer null wird und null mal null immer noch null ist! Die Parabel hat den Scheitelpunkt $S(2\vert 0)$.
Die Graphen solcher Parabeln könntest du sogar mit einer (selbstgebastelten) Parabelschablone zeichnen. Dabei legst du den unteren Punkt der Schablone auf den Scheitelpunkt und zeichnest dann an der Schablone entlang.
Alle Videos zum Thema
Videos zum Thema
Quadratische Funktionen: Normalparabel, Streckung, Stauchung und Verschiebung (5 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Quadratische Funktionen: Normalparabel, Streckung, Stauchung und Verschiebung (5 Arbeitsblätter)
-
 f(x) = x² – Wertetabelle und Funktionsgraph: Die Normalparabel
PDF anzeigen
f(x) = x² – Wertetabelle und Funktionsgraph: Die Normalparabel
PDF anzeigen -
 Quadratische Funktionen – Streckung und Stauchung
PDF anzeigen
Quadratische Funktionen – Streckung und Stauchung
PDF anzeigen -
 Quadratische Funktionen – Verschiebung entlang der y-Achse
PDF anzeigen
Quadratische Funktionen – Verschiebung entlang der y-Achse
PDF anzeigen -
 Quadratische Funktionen – Verschiebung entlang der x-Achse
PDF anzeigen
Quadratische Funktionen – Verschiebung entlang der x-Achse
PDF anzeigen -
 Quadratische Funktionen – Streckung, Stauchung und Verschiebung
PDF anzeigen
Quadratische Funktionen – Streckung, Stauchung und Verschiebung
PDF anzeigen
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Winkelsummen in Dreiecken und Vierecken – Übungen






















