Goldener Schnitt
in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.

Lerntext zum Thema Goldener Schnitt
Was ist der Goldene Schnitt?
Der Goldene Schnitt ist ein Phänomen, das sich in vielen Bereichen unserer Welt wiederfindet. Es handelt sich dabei um ein Verhältnis zwischen zwei Streckenlängen, das für das menschliche Auge als besonders ansprechend empfunden wird. Dementsprechend findet der Goldene Schnitt insbesondere in Bereichen wie Kunst oder Architektur Anwendung. Schau dir beispielsweise das Alte Rathaus in Leipzig an:

Der Turm teilt das Gebäude in einem ästhetischen Verhältnis, im Goldenen Schnitt. Doch was heißt das eigentlich?
Goldener Schnitt – Definition
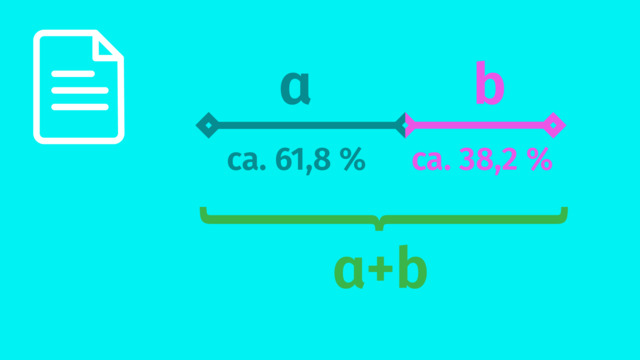
Mithilfe der Mathematik kann man das Phänomen sehr präzise beschreiben. Der Goldene Schnitt stellt das Teilungsverhältnis einer Strecke durch zwei Teilstrecken $a$ und $b$ dar. $a$ ist dabei die größere und $b$ die kleinere Teilstrecke.
$\dfrac{a}{b} = \dfrac{a~+~b}{a}$
In Worten beschrieben heißt das:
Das Verhältnis von der längeren Teilstrecke $a$ zur kürzeren Teilstrecke $b$ ist gleich dem Verhältnis der Gesamtstrecke (der Summe von $a$ und $b$) zur längeren Teilstrecke $a$.
Per Definition ist $a$ die größere Teilstrecke. Würde man $b$ per Definition als größere Strecke betrachten, müsste man die Gleichung umformulieren zu $\dfrac{b}{a} = \dfrac{a + b}{b}$.
Goldener Schnitt – Konstruktion
Wir können den Goldenen Schnitt zu einer gegebenen Strecke auch konstruieren. Dazu zeichnen wir uns zunächst eine Strecke $s$, die die Punkte $A$ und $B$ miteinander verbindet. Wir möchten diese Strecke $s$ nun so teilen, dass sie die Summe zweier Strecken $a$ und $b$ ist, deren Längen im Verhältnis des Goldenen Schnitts stehen. Dafür konstruieren wir zunächst mithilfe dieser Strecke $s$ ein rechtwinkliges Dreieck mit der Höhe $\dfrac{s}{2}$.

Vom neuen Punkt $C$ aus zeichnen wir einen Kreisbogen mit dem Radius $\dfrac{s}{2}$ und erhalten so den Schnittpunkt $D$ mit der Hypotenuse.

Zuletzt zeichnen wir noch einen Kreisbogen mit dem Mittelpunkt $A$ und dem Radius $\vert AD \vert$, also der Länge der Strecke zwischen $A$ und $D$.

Der Schnittpunkt S dieses Kreisbogens mit der Strecke $s$ teilt die Strecke zwischen $A$ und $B$ im Goldenen Schnitt. Die längere Teilstrecke zwischen $A$ und $S$ ist dabei $a$, die kürzere Teilstrecke zwischen $S$ und $B$ ist unser $b$.
Goldener Schnitt – Beweis
Wir wollen nun den Goldenen Schnitt mithilfe der obigen Konstruktion und damit mit dem Satz des Pythagoras beweisen. Wir stellen zunächst den Satz des Pythagoras mit den obigen Beziehungen auf: Die beiden Katheten kennen wir. Sie haben die Länge $s$ und $\dfrac{s}{2}$. Auch die Hypotenuse kennen wir aufgrund unserer Konstruktion. Die Länge der Hypotenuse ist gleich $\dfrac{s}{2}$ (Radius unseres ersten Kreisbogens) plus $a$ (Radius unseres zweiten Kreisbogens). Mit diesen Werten stellen wir nun eine Gleichung auf, die dem Satz des Pythagoras entspricht, und formen diese um.
$\begin{array}{rccccccl} s^2 & + & (\dfrac{s}{2})^2 & = & (a & + & \dfrac{s}{2})^2 & \\ \\ s^2 & + & \dfrac{s^2}{4} & = & (a & + & \dfrac{s}{2})^2 & \\ \\ s^2 & \cdot & (1 + \dfrac{1}{4}) & = & (a & + & \dfrac{s}{2})^2 & \\ \\ s^2 & \cdot & \dfrac{5}{4} & = & (a & + & \dfrac{s}{2})^2 & \vert \sqrt{ } \\ \\ s & \cdot & \dfrac{\sqrt{5}}{2} & = & a & + & \dfrac{s}{2} & \vert – \dfrac{s}{2} \\ \\ s & \cdot & \dfrac{\sqrt{5}}{2} – \dfrac{s}{2} & = & a & & & \\ \\ s & \cdot & (\dfrac{\sqrt{5}}{2} – \dfrac{1}{2}) & = & a & & & \\ \\ s & \cdot & (\dfrac{\sqrt{5}~–~1}{2}) & = & a & & & \vert s = a + b \\ \end{array}$
Nun können wir den Fakt nutzen, dass $s = a + b$ ist (unsere Gesamtstrecke $s$ ist gleich der Summe der Teilstrecken $a$ und $b$).
$\begin{array}{rccccl} (a + b) & \cdot (\dfrac{\sqrt{5}~–~1}{2}) & = & a & & \vert \cdot \dfrac{2}{\sqrt{5}~–~1}\\ \\ a + b & & = & a & \cdot \dfrac{2}{\sqrt{5}~–~1} & \vert : a\\ \\ \dfrac{a + b}{a} & & = & & \dfrac{2}{\sqrt{5}~–~1} & \\ \end{array}$
Wir haben nun gezeigt, dass $\dfrac{a + b}{a} = \dfrac{2}{\sqrt{5}~–~1}$ ist. Wenn wir jetzt noch durch die obige Gleichung zeigen, dass $\dfrac{a}{b} = \dfrac{2}{\sqrt{5}~–~1}$ ist, haben wir dadurch bewiesen, dass $\dfrac{a + b}{a} = \dfrac{a}{b}$ gilt. Wir beginnen wieder bei der vorletzten Zeile der letzten Gleichungsumformung.
$\begin{array}{rccccccl} a & + & b & = a & \cdot & \dfrac{2}{\sqrt{5}~–~1} & & \vert – a \\ \\ & & b & = a & \cdot & \dfrac{2}{\sqrt{5}~–~1} & – a & \\ \\ & & b & = a & \cdot & (\dfrac{2}{\sqrt{5}~–~1} – 1) & & \\ \\ & & b & = a & \cdot & (\dfrac{2}{\sqrt{5}~–~1} – \dfrac{\sqrt{5}~–~1}{\sqrt{5}~–~1}) & & \\ \\ & & b & = a & \cdot & \dfrac{3~–~\sqrt{5}}{\sqrt{5}~–~1} & & \vert : a \\ \\ & & \dfrac{b}{a} & = & \dfrac{3~–~\sqrt{5}}{\sqrt{5}~–~1} & & \vert \text{Kehrwert bilden} \\ \\ & & \dfrac{a}{b} & = & \dfrac{\sqrt{5}~–~1}{3~–~\sqrt{5}} & & \\ \end{array}$
Das ist noch nicht das Ergebnis, das wir haben wollen. Woran liegt das? Wie jeder andere Bruch auch kann dieser, auch wenn er mit den Wurzeln recht kompliziert aussieht, erweitert werden. Da wir auf $\dfrac{2}{\sqrt{5}~–~1}$ kommen wollen, müssen wir den Bruch mit einem Term erweitern, der die Wurzel aus dem Zähler entfernt. Das schaffen wir in diesem Fall mit der dritten binomischen Formel. Also erweitern wir und formen wieder um:
$\begin{array}{rcl} \dfrac{a}{b} & = & \dfrac{\sqrt{5}~–~1}{3~–~\sqrt{5}} \\ \\ \dfrac{a}{b} & = & \dfrac{(\sqrt{5}~–~1) \cdot (\sqrt{5} + 1)}{(3~–~\sqrt{5}) \cdot (\sqrt{5} + 1)} \\ \\ \dfrac{a}{b} & = & \dfrac{5~–~1}{3\sqrt{5} + 3~–~5~–~\sqrt{5}} \\ \\ \dfrac{a}{b} & = & \dfrac{4}{2\sqrt{5}~–~2} \\ \\ \dfrac{a}{b} & = & \dfrac{2}{\sqrt{5}~–~1} \\ \end{array}$
Jetzt haben wir einerseits gezeigt, dass $\dfrac{a + b}{a} = \dfrac{2}{\sqrt{5}~–~1}$ gilt, und andererseits gezeigt, dass $\dfrac{a}{b} = \dfrac{2}{\sqrt{5}~–~1}$ gilt. Damit haben wir bewiesen, dass unsere Konstruktion die Ausgangsstrecke im Goldenen Schnitt $\left(\dfrac{a}{b} =\dfrac{a + b}{a}\right)$ teilt. Zudem haben wir nebenbei den Wert dieses speziellen Verhältnisses berechnet. Es ist $\dfrac{2}{\sqrt{5}~–~1} \approx 1{,}618$.
Goldener Schnitt – Zusammenhang mit der Fibonacci-Folge
Da der Wert des Goldenen Schnitts eine irrationale Zahl ist, kann sie nicht durch einen Bruch ganzer Zahlen dargestellt werden. Man kann sich aber durch die sogenannte Fibonacci-Folge an die Zahl annähern. Zur Erinnerung:
Die Fibonacci-Folge ist eine Zahlenfolge, die sich durch die Summe der beiden vorhergehenden Zahlen ausdrückt:
$f_{n} = f_{n~–~1} + f_{n~–~2}$
Dabei ist $n \geq 3$ und $f_{1} = f_{2} = 1$.
Je größer die Zahlen der Folge werden, desto eher nähert sich der Quotient zweier aufeinanderfolgender Folgenglieder dem Goldenen Schnitt $\dfrac{2}{\sqrt{5}~–~1} \approx 1{,}618$ an. Wir schauen uns das einmal anhand der ersten Folgenglieder an:
| $n$ | $f_{n}$ | $\dfrac{f_{n + 1}}{f_{n}}$ |
|---|---|---|
| $1$ | $1$ | $\dfrac{1}{1} = 1$ |
| $2$ | $1$ | $\dfrac{2}{1} = 2$ |
| $3$ | $2$ | $\dfrac{3}{2} = 1{,}5$ |
| $4$ | $3$ | $\dfrac{5}{3} \approx 1{,}667$ |
| $5$ | $5$ | $\dfrac{8}{5} = 1{,}6$ |
| $6$ | $8$ | $\dfrac{13}{8} = 1,625$ |
| $7$ | $13$ | $\dfrac{21}{13} \approx 1,615$ |
| $8$ | $21$ | $\dfrac{34}{21} \approx 1,619$ |
| $9$ | $34$ | $\dfrac{55}{34} \approx 1,618$ |
| $10$ | $55$ | $\dfrac{89}{55} \approx 1,618$ |
Goldener Schnitt – Zusammenfassung
Der Goldene Schnitt lässt sich mathematisch durch die Beziehung zweier Streckenlängen $a$ und $b$ ausdrücken, wobei $a$ die größere Streckenlänge ist:
$\dfrac{a}{b} = \dfrac{a + b}{a} = \dfrac{2}{\sqrt{5}~–~1} \approx 1,618$
Der Goldene Schnitt kann als irrationale Zahl durch die Fibonacci-Folge sehr gut angenähert werden. Die Quotienten zweier aufeinanderfolgender Glieder der Fibonacci-Folge $a_n$ nähern sich mit zunehmendem $n$ dem Goldenen Schnitt an.
Goldener Schnitt Übung
-
Vervollständige den Text über den Goldenen Schnitt.
TippsVersuche, die Formel einmal selbst in Worte zu fassen.
Die Gesamtstrecke wird durch $s=a+b$ beschrieben, wobei $a$ länger ist als $b$.
Das Verhältnis wird angegeben in "längere Strecke durch kürzere Strecke".
LösungDer Turm des Alten Rathauses in Leipzig teilt das Gebäude in einem ganz besonderen Verhältnis. Du kannst erkennen, dass der Rathausturm nicht ganz in der Mitte steht, was auf den Betrachter eine besondere Wirkung hat.
Das Gebäude wird von dem Turm in eine längere Strecke $a$ und eine kürzere Strecke $b$ geteilt. Das Längenverhältnis der beiden Strecken nennt sich Goldener Schnitt.
Die Formel lautet $\frac {a}{b}= \frac{a+b}{a}$.
In Worten bedeutet dies, dass zwei Teilstrecken $a$ und $b$ einer Strecke $s$ dann im Verhältnis des Goldenen Schnittes diese Strecke teilen, wenn die längere Strecke $a$ zur Strecke $b$ im gleichen Verhältnis steht wie die Gesamtstrecke $a+b$ zur längeren Strecke $a$.
-
Forme die Gleichung schrittweise um, bis du das Verhältnis des Goldenen Schnittes erhältst.
TippsDas Verhältnis des Goldenen Schnittes ist $\frac {a+b}{a} = \frac{2}{\sqrt5 -1}$.
Gehe die Rechenschritte selbst einmal auf einem Zettel durch.
LösungEine Strecke $s$ wurde im Verhältnis des Goldenen Schnittes geteilt.
Es gilt dabei $ s= a+b$.
Das Dreieck, das du siehst, ist rechtwinklig. Daher gilt der Satz des Pythagoras:
$s^2 + (\frac{s}{2})^2 = (a+ \frac{s}{2})^2$
$\begin{align} s^2 +\frac{s^2}{4}&= (a+ \frac{s}{2})^2 \\ s^2 (1+\frac{1}{4} )&= (a+ \frac{s}{2})^2 \\ s^2 \cdot \frac{5}{4} &= (a+ \frac{s}{2})^2 &|& \sqrt{~} \\ s \cdot \frac{\sqrt{5}}{2} &=a + \frac{s}{2} &|& -\frac{s}{2} \\ s \cdot \frac{\sqrt5} {2} - \frac{s}{2}& = a \\ s \cdot ( \frac{\sqrt5} {2} - \frac{1}{2} )& = a \\ s \cdot \frac{\sqrt5 -1} {2} & = a &|& \text{da } s=a+b \\ (a+b) \cdot \frac{\sqrt5 -1} {2}& = a &|& :a \\ \frac {a+b}{a} \cdot \frac{\sqrt5 -1} {2}& = 1 \\ \frac {a+b}{a} \cdot \frac{\sqrt5 -1} {2}& = 1 &|& \cdot \frac{2}{\sqrt5 -1}\\ \frac {a+b}{a} & = \frac{2}{\sqrt5 -1} \end{align}$
-
Ermittle die fehlende Teilstrecke so, dass sich beide Teilstrecken im Goldenen Schnitt teilen.
TippsAchte darauf, die Einheit nicht zu vergessen.
Für eine Strecke $s=a+b$ gilt, sofern sie im Goldenen Schnitt geteilt wird:
$\frac{a+b}{a} = \frac{a}{b}$
Dabei ist $a$ die längere und $b$ die kürzere Teilstrecke.
Nutze den Ansatz aus dem zweiten Tipp und setze $a=3 ~cm$ ein. Löse dann die sich durch Umstellen ergebende quadratische Gleichung.
LösungFür eine Strecke $s=a+b$ gilt, sofern sie im Goldenen Schnitt geteilt wird:
$\frac{a+b}{a} = \frac{a}{b}$
Dabei ist $a$ die längere und $b$ die kürzere Teilstrecke.
Diesen Ansatz benutzt man, um die Aufgabe zu lösen.
Zuerst setzt man für $a$ die Länge $3$ ein und formt dann zur Normalform einer quadratischen Gleichung um.
$\begin{align} \frac{3}{b} & = \frac {3 + b}{3} &|& \cdot 3 \\ \frac{9}{b} & = 3 +b &|& \cdot b \\ 9 &= 3\cdot b + b^2 &|& - 9 \\ 0 & = b^2 + 3\cdot b - 9 &~& \end{align}$
Nun kann die Gleichung mittels der p-q-Formel oder auch mithilfe der Mitternachtsformel gelöst werden.
$\begin{align} b_{1/2} & = - \frac{3}{2} \pm \sqrt{(\frac{3}{2})^2 - (-9)} \\ & = -1,5 \pm \sqrt{1,5^2 +9} \\ & = -1,5 \pm \sqrt{2,25 +9} \\ & = -1,5 \pm \sqrt{11,25} \end{align}$
Daraus ergeben sich die zwei Lösungen:
$\begin{align} b_1 & =& -1,5 + \sqrt{11,25} \\ b_2 & =& -1,5 - \sqrt{11,25}. \end{align}$
Lösung $b_2 = -1,5 - \sqrt{11,25}$ kann bei dieser Aufgabe außer Acht gelassen werden, da sie negativ ist und Strecken immer positiv sind.
$b_1 = -1,5 + \sqrt{11,25} \approx 1,854$ ist die Lösung der Aufgabe.
Nun fehlt nur noch die Einheit: $b \approx 1,854~cm$.
Machen wir die Probe:
$\begin{align} \frac{3~cm}{1,854 ~cm} & = \frac{3~cm+1,854~cm}{3~cm} \\ 1,618 &= 1,618. \end{align} $
-
Entscheide, welche Darstellung des Verhältnisses $\Phi$ des Goldenen Schnittes richtig ist.
TippsLöse die Gleichung $x^2-x-1=0$ nach $x$ auf.
Es gilt: $x= \sqrt{1+x}$
Versuche nun, einen der oben aufgeführten Wurzelterme aufzustellen.
LösungDas Verhältnis $\Phi = \frac{\sqrt{5}+1}{2} \approx 1,618$ ist Lösung der Gleichung $x^2-x-1=0$.
Löst man diese Gleichung nach $x$ auf, so erhält man:
$x= \sqrt{1+x}$
Setzt man nun für das $x$ im Radikanden wieder $\sqrt{1+x}$ ein, so ergibt sich der Term:
$x=\sqrt{1+\sqrt{1+\sqrt{1+\sqrt{1+\sqrt{1+...}}}}}$
Es gilt auch $x=\Phi$, da $\Phi$ Lösung der quadratischen Gleichung ist. Somit gilt:
$\Phi = \frac {1}{ \sqrt{1+ \sqrt{1+ \sqrt{1+ \sqrt{1 + ...}}}}}$
Die zweite Lösung ist somit richtig.
-
Ermittle die Reihenfolge der Schritte, um eine Strecke im Verhältnis des Goldenen Schnittes zu teilen.
TippsMache dir noch einmal die gelernten Schritte zum Teilen einer Strecke im Goldenen Schnitt klar.
Bei allen Zeichnungen kannst du erkennen, ob eine andere Zeichnung vorher und nachher kommen müsste.
Die zweite Kathete hat im Vergleich zur längeren Kathete die Länge $\large{\frac s 2}$.
LösungUm eine Strecke $s$ im Verhältnis des Goldenen Schnittes zu teilen, zeichnet man zuerst ein rechtwinkliges Dreieck so, dass $s$ die längere Kathete ist und die andere Kathete $\frac{s}{2}$ lang ist.
Dann zeichnet man um den oberen Eckpunkt einen Kreis mit dem Radius $\frac{s}{2}$. Der Kreis schneidet die Hypotenuse, die längste Seite des Dreiecks, in einem Punkt $P$.
Nun setzt man den Zirkel an dem linken Eckpunkt an und zeichnet einen Kreis so, dass er den Punkt $P$ berührt. Der Schnittpunkt dieses Kreises mit der Ausgangsstrecke $s$ ist hier mit $T$ bezeichnet.
$T$ teilt die Strecke $s$ im Goldenen Schnitt.
-
Begründe, weshalb das Seitenverhältnis von Schenkel zu Grundseite des Goldenen Dreiecks der Goldene Schnitt ist.
TippsWas gilt für die Innenwinkel eines Dreiecks?
In Dreiecken gilt der Innenwinkelsummensatz $\alpha + \beta + \gamma = 180°$.
LösungDas Goldene Dreieck ist gleichschenklig. Die Winkel zwischen Grundseite und Schenkeln sind $72°$ groß. Dann ist der Winkel zwischen den beiden Schenkeln $36°$ groß.
Es gilt nämlich der Innenwinkelsummensatz: $\alpha + \beta + \gamma = 180°$ bzw. $\gamma = 180° - \alpha - \beta$.
Daraus ergibt sich, dass $\gamma$ hier $36°$ groß ist.
Zeichnet man nun eine Winkelhalbierende des Winkels bei Eckpunkt A, so entsteht ein zum Dreieck ABC ähnliches Dreieck ABD, weil beide Dreiecke gleich große Winkel haben.
Es gilt somit der Ähnlichkeitssatz www.
Für das nun entstandenen Dreieck ABD gilt: $BD = x-g$.
Das Dreieck ADC ist gleichschenklig, da die Winkel bei den Punkten A und C $36°$ groß sind. Deshalb hat die Strecke CD auch die Länge $g$ und die Strecke BD die Länge $x-g$.
Da die Dreiecke ABC und ABD ähnlich zueinander sind, gilt folgendes Seitenverhältnis: $\frac{x}{g} = \frac{g}{x-g}$.
Betrachtet man $x+g$ als eine Strecke, so bildet dieses Verhältnis den Goldenen Schnitt.
9.711
sofaheld-Level
6.600
vorgefertigte
Vokabeln
8.276
Lernvideos
38.589
Übungen
33.616
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Klassenstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung


 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?