Strecken in gleiche Teile teilen

Strecken in gleiche Teile teilen Übung

• Beschreibe, wie du die Strecke $\overline{AB}$ in gleich große Teile teilst.

  Tipps

  Um eine Strecke in gleich große Teile zu teilen, brauchst du zunächst einen Hilfsstrahl.

  Mithilfe der gleich großen Teilstrecken auf dem Hilfsstrahl kannst du gleich große Teilstrecken auf der Strecke $\overline{AB}$ konstruieren.

  Lösung

  Möchtest du eine Strecke $\overline{AB}$ in vier gleich große Teile teilen, so gehst du wie folgt vor:

  1. Zeichne einen Hilfsstrahl, der im Punkt $A$ der Strecke beginnt und in einem spitzen Winkel zur Strecke verläuft. Dieser sollte nicht zu kurz gewählt werden.
  2. Trage mit einem Zirkel $4$ gleich lange Strecken auf dem Hilfsstrahl ab. Achte darauf, dass sich dabei die Zirkeleinstellung nicht ändert. Zeichne hierzu mit dem Zirkel einen Kreisbogen um den Punkt $A$, der den Hilfsstrahl schneidet. Stich in dem Schnittpunkt wieder ein und zeichne einen weiteren Kreisbogen, der den Hilfsstrahl schneidet. Wiederhole diesen Konstruktionsschritt, bis du vier Schnittpunkte auf dem Hilfsstrahl erhältst, die alle denselben Abstand zueinander haben.
  3. Zeichne mit einem Geodreieck eine Gerade durch den letzten Schnittpunkt auf dem Hilfsstrahl und den Endpunkt $B$ auf der Strecke $\overline{AB}$.
  4. Führe drei Parallelverschiebungen dieser Geraden durch die restlichen Schnittpunkte auf dem Hilfsstrahl durch. Nutze dafür zwei Geodreiecke, die du aneinander legst. Das erste Geodreieck bleibt dabei zunächst an der Geraden liegen, die du parallel verschieben möchtest. Das zweite Geodreieck dient als Führung und darf nicht verrutschen. Verschiebe das erste Geodreieck entlang des zweiten bis zum nächsten Schnittpunkt auf dem Hilfsstrahl und zeichne dort eine weitere Gerade. Wiederhole diesen Schritt noch zweimal.
  5. Die resultierenden vier Parallelen teilen nun die Strecke $\overline{AB}$ in vier gleich große Abschnitte.

  Das Endergebnis kannst du der Abbildung entnehmen.

• Gib an, welche Eigenschaften bei der Teilung der Strecke $\overline{AB}$ in gleiche Teile vorliegen.

  Tipps

  Teilst du eine Strecke in gleich lange Abschnitte, so zeichnest du zunächst einen Hilfsstrahl, welchen du mit einem Zirkel in Teilstrecken teilst. Dabei entspricht die Länge der Teilstrecken deinem Zirkelradius, welchen du nicht ändern darfst.

  Auf die hier abgebildete Figur ist der Strahlensatz anwendbar, weil die beiden gelben Strecken parallel zueinander sind. Ist $\overline{AE}=\overline{ED}$ so gilt nach dem Strahlensatz:

  $\overline{AB}=\overline{BC}$.

  Lösung

  Wenn wir eine Strecke $\overline{AB}$ in gleich lange Abschnitte teilen möchten, so zeichnen wir zunächst einen Hilfsstrahl, welchen wir mit einem Zirkel in gleich lange Teilstrecken teilen.

  Doch warum teilen wir den Hilfsstrahl in gleich lange Teilstrecken, wenn wir eigentlich die Strecke $\overline{AB}$ in gleich lange Abschnitte teilen möchten?

  Das folgt aus dem Strahlensatz. Der Strahlensatz gilt, wenn zwei Strahlen im gleichen Punkt beginnen und von Parallelen geschnitten werden. Sind die Teilstrecken auf dem Hilfsstrahl alle gleich lang, so folgt mit dem Strahlensatz, dass auch die Abschnitte auf der Strecke $\overline{AB}$ alle gleich lang sein müssen.

  Beachte, dass die Teilstrecken auf dem Hilfsstrahl und die auf der Strecke $\overline{AB}$ nicht gleich lang sein müssen.

  Diese Konstruktion funktioniert für jede Anzahl von Abschnitten, ohne dass wir uns um den genauen Winkel des Hilfsstrahls oder den Radius am Zirkel kümmern müssen.

• Bestimme, wie viele Kreisbögen du zum Teilen der Strecke $\overline{AB}$ in gleich lange Abschnitte auf dem Hilfsstrahl abträgst.

  Tipps

  Überlege, ob die Punkte $A$ und $B$ der Strecke $\overline{AB}$ in der gegebenen Zahl bereits enthalten sind oder nicht.

  Liegen auf einer Strecke $\overline{AB}$ inklusive Anfangs- und Endpunkt insgesamt $n$ Punkte in gleichen Abständen, so sind zwischen diesen $n-1$ Abstände.

  Schau dir folgendes Beispiel an:

  Auf einem Sportplatz sollen sich $5$ Läufer auf einer Strecke $\overline{AB}$ in gleichen Abständen aufstellen. Dabei steht der erste Läufer auf dem Punkt $A$ und der letzte Läufer auf dem Punkt $B$. Zwischen diesen beiden Läufern stehen also drei weitere. Demnach wird die Strecke und somit auch der Hilfsstrahl in $4$ gleich lange Teilstrecken geteilt.

  Lösung

  Liegen auf einer Strecke $\overline{AB}$ inklusive Anfangs- und Endpunkt insgesamt $n$ Punkte in gleichen Abständen, so sind zwischen diesen $n-1$ Abstände. Wenn wir also wissen, wie viele Punkte auf den jeweiligen Strecken liegen, dann können wir die Anzahl der gleich langen Abschnitte auf dem Hilfsstrahl ableiten.

  Mülleimer-Problem

  Wir betrachten zunächst das Mülleimer-Problem. Auf dem geraden Schulweg $\overline{AB}$ von Lena sollen zwei Mülleimer in gleich großen Abständen aufgestellt werden. Wobei sich in den Punkten $A$ und $B$ bereits je ein Mülleimer befindet.

  Somit möchten wir auf der Strecke $\overline{AB}$ inklusive Anfangs- und Endpunkt der Strecke insgesamt $4$ Mülleimer haben, die Strecke also in $3$ gleich lange Abschnitte teilen. Hierzu müssen wir auf dem Hilfsstrahl $3$ Kreisbögen abtragen.

  Ballon-Problem

  Für eine Geburtstagsparty sollen an einem Faden $\overline{AB}$ drei Luftballons in gleichen Abständen befestigt werden. Wir haben also inklusive Anfangs- und Endpunkt der Strecke $\overline{AB}$ drei Befestigungspunkte.

  Die Strecke $\overline{AB}$ sowie der Hilfsstrahl müssen also in je $2$ gleich lange Abschnitte geteilt werden.

• Zeige alle Zeichnungen, bei denen die Strecke $\overline{AB}$ korrekt in $n$ gleiche Teile geteilt wurde.

  Tipps

  Man trägt mit einem Zirkel $n$ gleich lange Strecken auf dem Hilfsstrahl ab.

  Man verbindet den letzten Schnittpunkt auf dem Hilfsstrahl mit dem Endpunkt $B$ der Strecke $\overline{AB}$.

  Dann führt man $n-1$ Parallelverschiebungen dieser Geraden durch die restlichen Schnittpunkte auf dem Hilfsstrahl durch.

  Lösung

  Im Folgenden untersuchen wir die gegebenen Zeichnungen, in denen die Strecke $AB$ in $n$ gleich große Teile geteilt werden soll.

  Zeichnung 1
  Diese Zeichnung ist nicht korrekt, da die Strecke $\overline{AB}$ nicht in $3$, sondern $4$ gleich große Teilstrecken geteilt wurde.

  Zeichnung 2
  Diese Zeichnung ist korrekt. Die Strecke $\overline{AB}$ wurde wie angegeben in $4$ gleich große Teilstrecken geteilt.

  Zeichnung 3
  Diese Zeichnung ist nicht korrekt. Die Strecke $\overline{AB}$ wurde zwar wie angegeben in $4$ Teilstrecken geteilt, allerdings sind diese nicht gleich groß. Das liegt daran, dass die Parallelverschiebung nicht richtig gemacht wurde.

  Zeichnung 4
  Diese Zeichnung ist nicht korrekt, da die Strecke $\overline{AB}$ nicht in $4$, sondern $3$ gleich große Teilstrecken geteilt wurde.

  Zeichnung 5
  Diese Zeichnung ist korrekt. Die Strecke $\overline{AB}$ wurde wie angegeben in $3$ gleich große Teilstrecken geteilt.

• Gib das zu verwendende Hilfsmittel an.

  Tipps

  Im Bereich der Konstruktion werden Längen mit einem Zirkel abgetragen.

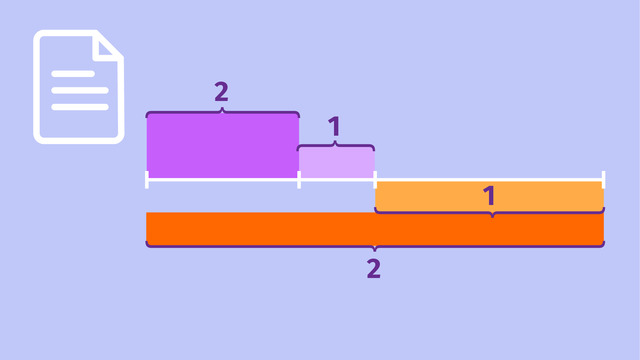
  Teilt man eine Strecke in einem Verhältnis von $3:2$, so führt man ebenfalls eine Parallelverschiebung durch. Diese kannst du der Abbildung entnehmen.

  Lösung

  Wenn wir eine Strecke $\overline{AB}$ in $n$ gleich lange Abschnitte teilen möchten, so brauchen wir für die einzelnen Konstruktionsschritte bestimmte Hilfsmittel.

  1. Wir zeichnen mit Hilfe von einem Geodreieck einen Hilfsstrahl.
  2. Wir tragen mit Hilfe von einem Zirkel gleich lange Teilstrecken auf dem Hilfsstrahl ab.
  3. Wir führen mit Hilfe von zwei Geodreiecken Parallelverschiebungen durch.

  Für solch eine Konstruktion genügen also Zirkel und Geodreieck.

• Ermittle die gesuchte Anzahl an Abschnitten.

  Tipps

  Die Länge einer Strecke setzt sich wie folgt zusammen:

  Streckenlänge $=$ Anzahl gleich langer Abschnitte $\cdot$ Abschnittslänge.

  Eine Strecke, die du in $n$ gleich lange Abschnitte der Länge $a$ geteilt hast, hat eine Gesamtlänge von:

  $\overline{AB}=n\cdot a$.

  Möchtest du jedoch die Anzahl $n$ bestimmen, so formst du wie folgt um:

  $n=\overline{AB} : a$.

  Lösung

  Setzt sich eine Strecke $\overline{AB}$ aus $n$ gleich langen Abschnitten der Länge $a$ zusammen, so gilt:

  $\overline{AB}=n\cdot a$.

  Da in unserem Fall die Strecke $\overline{AB}=35\ \text{cm}$ und die Abschnittslänge $a=5\ \text{cm}$ gegeben sind, müssen wir umstellen zu:

  $n=\overline{AB} : a$.

  Dann erhalten wir:

  $n=35\ \text{cm}\ :\ 5\ \text{cm}=7$.

  Max hat die Strecke also in $7$ gleich lange Abschnitte geteilt.