Exponentielles Wachstum
Exponentielles Wachstum beschreibt einen Prozess, bei dem ein Wert in festen Abständen immer um den gleichen Faktor wächst, wie das Beispiel der Reiskornlegende zeigt. Interessiert? Erfahre mehr über spannende Beispiele wie Bakterienwachstum und die Ausbreitung von Viren im Text!
- Exponentielles Wachstum und exponentieller Zerfall – Einführung
- Was ist exponentielles Wachstum?
- Exponentielles Wachstum – Definition
- Exponentielles Wachstum – Beispiel
- Exponentielles Wachstum – Formel und Berechnung
in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.

Lerntext zum Thema Exponentielles Wachstum
Exponentielles Wachstum und exponentieller Zerfall – Einführung
Zur Einführung in die Bedeutung von exponentiellem Wachstum kannst du dir eine berühmte Geschichte anschauen, die sogenannte Reiskornlegende.
Wusstest du schon?
Ein Bakterium, das sich alle 20 Minuten teilt, könnte in nur einem Tag so viele Nachkommen produzieren, dass die gesamte Erde mit einer Schicht von Bakterien bedeckt würde! Zum Glück stoppt das Wachstum durch begrenzte Ressourcen. Das ist ein beeindruckendes Beispiel für exponentielles Wachstum!
Was ist exponentielles Wachstum?
Wir wollen zunächst Prozesse betrachten, bei denen ein bestimmter Wert (in unserem Beispiel ist das die Anzahl der Reiskörner) in bestimmten Abständen mit einen konstanten Faktor zunimmt.
Exponentielles Wachstum – Definition
In der Mathematik oder um Phänomene der Natur und aus dem Alltag zu verstehen, sind wir daran interessiert zu verstehen, wie Änderungsprozesse ablaufen. Dabei geht es speziell um die Wachstumsprozesse und Zerfallsprozesse (die wir auch negative Wachstumsprozesse nennen). Wir wollen also verstehen, wie gewisse Werte in bestimmten Zeitabständen wachsen oder fallen. Ein wichtiger Änderungsprozess ist exponentielles Wachstum.
Bei einem Wachstumsprozess handelt es sich um exponentielles Wachstum, wenn sich der Wert in gleichen Abständen immer um den gleichen Faktor vergrößert (oder verkleinert).
Exponentielles Wachstum – Beispiel
Wir schauen uns das Ganze an unserem Einführungs-Beispiel mit dem Schachbrett und den Reiskörnen noch einmal genauer an.
Auf dem ersten Feld liegt ein Reiskorn. Auf dem zweiten das Doppelte, also zwei Körner. Auch dieser Wert wird verdoppelt, sodass auf dem dritten Feld vier Körner liegen. Wir schreiben diese Rechenschritte in Formeln und stellen damit die rekursive Funktionsgleichung auf. $R$ steht dabei für die Anzahl an Reiskörnern und die Variable ist die Nummer des Felds:
$R(1) = 1$
$R(2) = 2 \cdot R(1) = 2$
$R(3) = 2 \cdot R(2) = 4$
$R(4) = 2 \cdot R(3) = 8$
$\downarrow ~\text{rekursive Funktionsgleichung}$
$R(n+1) = 2 \cdot R(n)$
Auf jedem Feld liegen genau doppelt so viele Reiskörner wie auf dem vorherigen. Deswegen wird der Wert eines Feldes $n$ mit $2$ multipliziert, um den Wert des nächsten Feldes zu erhalten. Die Zahlen wachsen also immer schneller. Schauen wir uns die Zahlen noch einmal in einer Tabelle an:
| Nummer des Felds | Anzahl an Reiskörnern |
|---|---|
| $1$ | $1$ |
| $2$ | $2$ |
| $3$ | $4$ |
| $4$ | $8$ |
| $5$ | $16$ |
| $6$ | $32$ |
| $7$ | $64$ |
| $8$ | $128$ |
| $9$ | $256$ |
| $10$ | $512$ |
| $11$ | $1\, 024$ |
| $12$ | $2\, 048$ |
| .... | |
| $62$ | $2\, 305\, 843\, 009\, 213\, 690\, 000$ |
| $63$ | $4\, 611\, 686\, 018\, 427\, 380\, 000$ |
| $64$ | $9\, 223\, 372\, 036\, 854\, 770\, 000$ |
Auf dem zwölften Feld hätten wir also schon $2\, 048$ Reiskörner – das Schachbrett müsste schon ziemlich groß sein, damit diese Menge in ein Feld passt. Und das Schachbrett hat ja noch wesentlich mehr Felder, $64$ um genau zu sein. Und auf dem $64.$ Feld müssten schon sehr, sehr viele Reiskörner liegen, und zwar:
$9\, 223\, 372\, 036\, 854\, 775\, 808$
Es ist aber natürlich mühsam, $64$-mal den Wert zu verdoppeln, selbst wenn wir es mit einem Taschenrechner machen. Deswegen werfen wir noch einmal einen genauen Blick auf die Zahlen. Da sich die Werte jedes mal um den Faktor $2$ vergrößern, wissen wir, dass es sich um Zweierpotenzen handelt:
- Feld: $~1 = 2^{0}$
- Feld: $~2 = 2^{1}$
- Feld: $~4 = 2^{2}$
- Feld: $~8 = 2^{3}$
- Feld: $~16 = 2^{4}$
... und so weiter. So können wir die explizite Funktion bestimmen. In diesem Fall ist das eine Exponentialfunktion mit der Basis $2$, auch Wachstumsfaktor genannt, und dem Anfangswert $1$:
$n$. Feld: $~R(n) = 2^{n-1} \quad \text{mit} \quad n=[1,2,3, ..., 64]$
Diese Form des Wachstums wird auch exponentielles Wachstum genannt, weil die Variable im Exponenten steht.
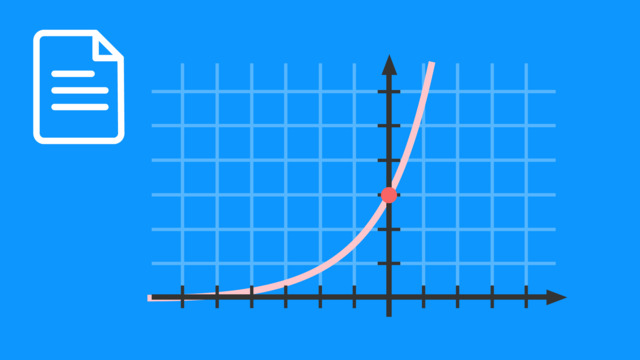
Grafisch dargestellt sieht diese Funktion so aus:
Wenn wir $n-1=x$ setzen, können wir die Funktion auch als $f(x)=2^{x}$ auffassen.
Kennst du das?
Vielleicht hast du schon einmal von einem Virus gehört, das sich sehr schnell ausbreitet. Zuerst infiziert eine Person ein paar wenige andere, aber bald können es Hunderte oder Tausende sein. Diese rasante Vermehrung ist ein Beispiel für exponentielles Wachstum. Aus einer einzelnen Infektion kann sehr schnell ein großes Problem werden, wenn die Anzahl der Infizierten sich ständig verdoppelt oder verdreifacht.
Exponentielles Wachstum – Formel und Berechnung
Natürlich können die Basis und der Anfangswert auch ganz unterschiedliche Werte annehmen. Die allgemeine Form einer Exponentialfunktion sieht folgendermaßen aus:
$f(x) = a \cdot b^{x}$
Dabei ist $a$ der Anfangswert, $b$ die Basis oder der Wachstumsfaktor und $x$ die unabhängige Variable.
Im Kontext von exponentiellem Wachstum wird für die unabhängige Variable oft auch ein $t$ gewählt, das für time steht. Die Formel lautet dann z. B. $B(t)=B(0)\cdot a^{t}$, wobei
- $B(t)$ der Bestand zum Zeitpunkt $t$ ist.
- $B(0)$ der Anfangsbestand (Bestand zum Zeitpunkt $t=0$) ist.
- $a$ der Wachstumsfaktor ist ($a = 1 + r$, wobei $r$ die Wachstumsrate ist).
- $t$ die Anzahl der Zeitintervalle ist.
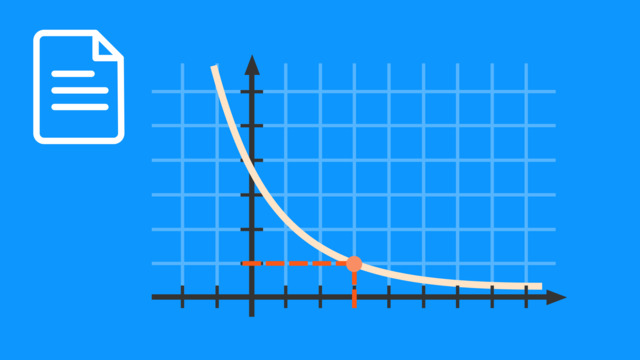
Exponentieller Zerfall
Ein Sonderfall des exponentiellen Wachstums ist der exponentielle Zerfall. Darunter werden Wachstums-Prozesse zusammengefasst, bei denen die Werte abnehmen.
Exponentieller Zerfall – Definition
In unserem Beispiel war der Wachstumsfaktor $b$ größer als eins. Er kann aber auch kleiner sein. In diesem Fall handelt es sich um einen exponentiellen Zerfall und der Wachstumsfaktor wird Zerfallsfaktor genannt. Die Form der Funktionsgleichung ändert sich dabei nicht.
Es handelt sich um einen exponentiellen Zerfall, wenn die Basis zwischen $0$ und $1$ liegt. Also gilt: $0 < b < 1$
Exponentieller Zerfall – Beispiel
Wir betrachten den Zerfall von Plutonium-239. Es handelt sich dabei um ein radioaktives Isotop, das natürlich nur sehr selten vorkommt. Es wurde aber in den 60er-Jahren während der Atomwaffentests erzeugt und auf der ganzen Welt verteilt. Es zerfällt zu Uran-235 und sendet dabei Alphastrahlung aus. Dieser Prozess ist relativ langsam: Von $1\,000~\text{g}$ Pu-239 sind nach $1\,000$ Jahren noch ungefähr $972~\text{g}$ vorhanden. Es sind also $2{,}8\%$ zerfallen. Nach weiteren $1\,000$ Jahren zerfallen wiederum $2{,}8\%$ und so weiter. Wir können daraus wieder die rekursive und die explizite Funktionsgleichung aufstellen:
Rekursiv:
$\text{Pu-}239(n+1\, 000) = \text{Pu-}239(n) \cdot 0{,}972$
Explizit:
$\text{Pu-}239(n) = \text{Pu-}239(0) \cdot 0{,}972^{\frac{n}{1\,000}}$
In der expliziten Form teilen wir $n$ durch $1\,000$, weil wir den Wachstumsfaktor pro tausend Jahre angegeben haben. Es handelt sich hierbei um negatives Wachstum bzw. um einen Zerfall, denn die Plutonium-Menge wird immer kleiner. Nach $24\,110$ Jahren ist genau die Hälfte des Ausgangswerts erreicht. Diese Zeit wird deswegen auch die Halbwertszeit genannt.
Interaktiver Graph – Einfluss von Anfangswert und Wachstumsfaktor
Teste selbst, wie sich der Anfangswert $a$ und der Änderungsfaktor $b$ auf den Verlauf des Graphen auswirken.
$~$
Exponentielles Wachstum – weitere Beispiele
Das exponentielle Wachstum taucht in vielen Bereichen unseres Lebens auf.
Einige Beispiel sind:
- Das Wachstum von Bakterien, die sich durch Zellteilung vermehren, ist exponentiell.
- Die Ausbreitung von hochansteckenden Krankheiten, zum Beispiel bei der
Covid-19-Pandemie, folgt in der Regel einem exponentiellen Verlauf. Gerade diese schnelle Ausbreitung macht Krankheiten so gefährlich. - Die Zunahme der Weltbevölkerung war bis zu den 1970er-Jahren exponentiell, seitdem nimmt die Wachstumsrate insgesamt ab.
- Bei Abkühlungsvorgängen, beispielsweise einer Tasse Tee, handelt es sich um exponentiellen Zerfall. Am Anfang fällt die Temperatur des Tees sehr schnell ab, nähert sich dann aber immer langsamer der Umgebungstemperatur an.
Schlaue Idee
Wenn du Geld sparst, kannst du den Zinseszinseffekt nutzen. Hier wächst dein gespartes Geld exponentiell mit der Zeit, weil du immer wieder Zinsen auf deine bereits erhaltenen Zinsen bekommst.
Ausblick – das lernst du nach Exponentielles Wachstum
Vertiefe dein Verständnis der Exponentialfunktionen, mit denen sich exponentielles Wachstum beschreiben lässt. Weitere Themen wie die Logarithmusfunktion und geometrische Reihen sind ebenfalls eng mit der Exponentialfunktion verknüpft. Damit bekommst du Wachstum und Ausbreitung in den Griff!
Wenn du das Gelernte direkt anwenden möchtest, dann schau in den Übungstext zum Thema Exponentielles Wachstum an!
Zusammenfassung von exponentiellem Wachstum und Zerfall
- Als exponentielles Wachstum bezeichnen wir jedes positive oder negative Wachstum, das wir auf folgende Weise als Exponentialfunktion ausdrücken können:
$f(x) = a \cdot b^{x}$ - Für positives Wachstum gilt $b > 1$.
- Für negatives Wachstum (Zerfall) gilt $0 < b < 1$.
- Das exponentielle Wachstum überholt nach einer gewissen Zeit jedes andere Wachstum.
Häufig gestellte Fragen zum Thema Exponentielles Wachstum
Exponentielles Wachstum Übung
-
Beschreibe, in welchen Fällen es sich um exponentielles Wachstum handelt.
TippsEin Baum wird in den Garten gepflanzt. Zu diesem Zeitpunkt schaut er um $10 \text{ cm}$ aus dem Boden. Pro Jahr wächst er um ca. $25 \text{ cm}$. Das Wachstum des Baumes kann durch ein lineares Wachstum beschrieben werden:
$f(x)=25 \cdot x +10$
Bei einem exponentiellen Wachstum handelt es sich um eine konstante prozentuale Zunahme pro Zeiteinheit.
LösungDie folgenden Aussagen sind richtig:
- Legt ein Biologe eine Bakterienkolonie an, in der sich die Bakterien ungehindert teilen dürfen, handelt es sich um ein exponentielles Wachstum.
- Der radioaktive Zerfall kann mit einem exponentiellen Wachstum beschrieben werden, wenn die Basis $0<a<1$ gewählt wird.
- Bei der Weltbevölkerung handelt es sich um eine lineare Wachstumsfunktion.
- Der radioaktive Zerfall kann mit einem exponentiellen Wachstum beschrieben werden, wenn die Basis $a<0$ gewählt wird.
$f(1)=c\cdot (-2)^1=-2$ $f(2)=c\cdot (-2)^2=4$ $f(3)=c\cdot (-2)^3=-8$ $f(4)=c\cdot (-2)^4=16$ usw.
Für den radioaktiven Zerfall muss $0<a<1$ gelten.
- Ein Schwimmbecken wird mit Wasser gefüllt. Am Anfang sind $100$ Liter Wasser im Becken. Pro Minute laufen nun $20$ Liter Wasser in das Becken. Bei der Wasserzunahme handelt es sich um exponentielles Wachstum.
-
Stelle mit Hilfe der Wertepaare die rekursive und explizite exponentielle Funktion auf.
TippsEine Exponentialfunktion können wir allgemein beschreiben durch:
$f(x)=c\cdot a^x$, wobei $c$ der Anfangswert und $a$ die Basis ist.
Die rekursive Funktionsgleichung zeichnet sich dadurch aus, dass man vorherige Funktionswerte kennen muss. Das heißt, dass du zum Beispiel $f(n)$ anhand von $f(n-1)$ berechnest.
Bei der expliziten Funktionsgleichung kannst du das Ergebnis direkt berechnen.
LösungDer altindische Mathelehrer Budhiram gilt als Erfinder des Schachspiels. Als er es seinem König vorstellte, war dieser so begeistert, dass sich Budhiram eine beliebige Belohnung aussuchen durfte.
Er wollte nur etwas Bescheidenes: $1$ Reiskorn auf dem ersten Schachfeld, $2$ auf dem zweiten, $4$ auf dem dritten, $8$ auf dem vierten und so weiter bis das ganze Schachbrett fertig ist. Also auf jedem Feld doppelt so viele Reiskörner wie auf dem vorherigen.
Erst war der König beleidigt, da sich Budhiram auch Gold oder Diamanten hätte wünschen können, aber später stellte er fest, dass alle Reisspeicher des Landes nicht ausreichten. Rechnen wir mal nach. Dazu beschreibe $f(n)$ die Reiskörner auf dem $n$ -ten Schachfeld.
- $f(1)=1$
- $f(2)=2\cdot 1= 2$
- $f(3)=2\cdot 2= 4$
- $f(4)=2\cdot 4= 8$
- $f(5)=2\cdot 8= 16$
- $f(n+1)=2\cdot f(n)$
Anhand der rekursiven Funktionsgleichung können wir nun auch die explizite Funktionsgleichung bilden:
- $f(n)=2^{n-1}$
$f(64)=2^{64-1}= 9.223.372.036.854.775.808$
Addiert man alle Felder, übersteigt es bei weitem die Menge an Reis, die in $800$ Jahren weltweit produziert wird.
Dabei handelt es sich also um eine Exponentialfunktion und somit reden wir von einem exponentiellen Wachstum, da eine konstante prozentuale Zunahme von $100\%$ pro Feldeinheit vorliegt.
-
Entscheide, ob es sich um exponentiellen Zuwachs oder Zerfall handelt.
TippsBei einer Exponentialfunktion muss für die Basis $a$ gelten: $0<a$ und $a \neq 1$.
Bei $f(x)=4x^2$ liegt quadratisches Wachstum vor.
Bei $f(x)=5\cdot (0,1)^x$ handelt es sich um exponentiellen Zerfall, da die Basis kleiner als $1$ ist.
LösungDu kannst die Funktionsterme wie folgt zuordnen:
Exponentieller Zuwachs
Hierbei handelt es sich um eine Exponentialfunktion mit der Gleichung: $f(x)=c\cdot a^x$, wobei $c$ der Anfangswert ist und $a$ die Basis, die für einen Zuwachs größer als $1$ sein muss.
- $f(x)=2^{x-1}$, da wir es auch schreiben können als $2^{x-1}=2^x\cdot 2^{-1}= 2^x\cdot \frac12=\frac12 \cdot 2^x$.
- $f(x)=1,002\cdot (1,93)^x$
- $f(x)=c \cdot (1,001)^x$
Hierbei handelt es sich um eine Exponentialfunktion mit der Gleichung: $f(x)=c\cdot a^x$, wobei $c$ der Anfangswert ist und $a$ die Basis, die für einen Zerfall kleiner als $1$ sein muss.
- $f(x)=25\cdot (0,95)^x$
- $f(x)=37,2\cdot (0,37)^x$
- $f(x)=25\cdot (0,001)^x$
- $f(x)=25\cdot (-0,95)^x$: Bei einer Exponentialfunktion darf die Basis $a$ niemals negativ sein.
- $f(x)=x^2+3$: Hier liegt quadratisches Wachstum vor.
- $f(x)=c \cdot (1,0)^x$: Bei einer Exponentialfunktion muss die Basis $a$ immer ungleich $1$ sein, da $1$ hoch eine beliebige Zahl immer $1$ ist. Dieser Funktionsterm ist damit $c \cdot (1,0)^x=c \cdot 1 = c$ konstant.
-
Bestimme die Exponentialfunktion für das Wachstum oder den Zerfall.
TippsSo kannst du vorgehen:
Am Anfang leben $10$ Kaninchen im Park. Sie vermehren sich pro Jahr um $50\%$.
- Der Anfangswert beträgt hier $c=10$. Für die Basis der Exponentialfunktion betrachten wir die $50\%$ als Dezimalbruch $50\%=0,5$. Da die Kaninchenpopulation wächst, müssen wir $0,5$ zu einem Ganzen addieren:
- $a=1+0,5=1,5$
Steigt deine Menge, muss die Basis $a$ größer als $1$ sein, sinkt sie, muss $0<a<1$ gelten.
LösungEine Exponentialfunktion kann allgemein durch folgende Gleichung beschrieben werden:
$f(x)=c \cdot a^x$, wobei $c$ der Anfangswert und $a$ die Basis der Exponentialfunktion ist.
$1.$ Am Anfang sind $100$ Bakterien vorhanden. Die Bakterienkultur wächst in $1$ Stunde um $75\%$. Wie verläuft das Wachstum?
- Der Anfangswert beträgt hier $c=100$. Für die Basis betrachten wir die $75\%$ als Dezimalbruch $75\%=0,75$. Da die Bakterienkultur wächst, müssen wir dieses zu einem Ganzen, also zu $1$ addieren, um die Basis $a$ zu erhalten:
Damit ergibt sich als Exponentialfunktion:
$f(x)=100\cdot (1,75)^x$
$2.$ Zu Beginn lebten $75$ Aliens auf dem Planeten Pandeor. Pro Jahr wächst die Bevölkerung um $25\%$. Wie verläuft das Wachstum?
- Der Anfangswert beträgt hier $c=75$. Für die Basis betrachten wir die $25\%$ als Dezimalbruch $25\%=0,25$. Da die Bevölkerung wächst, müssen wir dieses wieder zu einem Ganzen addieren, um die Basis $a$ zu erhalten:
Damit ergibt sich als Exponentialfunktion:
$f(x)=75\cdot (1,25)^x$
$3.$ Ein radioaktiver Stoff zerfällt so, dass die ursprüngliche Masse von $75\text{ g}$ jährlich um $25\%$ abnimmt. Wie verläuft das Wachstum?
- Der Anfangswert beträgt hier $c=75$. Für die Basis betrachten wir die $25\%$ wieder als Dezimalbruch $25\%=0,25$. Da die Masse geringer wird, müssen wir diesen Wert diesmal von einem Ganzen abziehen, um die Basis $a$ zu erhalten:
Damit ergibt sich als Exponentialfunktion:
$f(x)=75\cdot (0,75)^x$
$4.$ Der Luftdruck der Erdatmosphäre nimmt um ungefähr $12 \%$ je $1 \text{ km}$ Höhenunterschied ab. Auf Höhe des Meeresspiegels beträgt er ungefähr $1,013\text{ bar}$. Wie entwickelt sich der Luftdruck mit zunehmender Höhe?
- Der Anfangswert beträgt hier $c=1,013$. Für die Basis betrachten wir die $12\%$ als Dezimalbruch $12\%=0,12$ und ziehen diesen für die Basis $a$ von einem Ganzen ab, da es sich um eine Abnahme handelt:
Damit ergibt sich als Exponentialfunktion:
$f(x)=1,013\cdot (0,88)^x$
-
Bestimme, bei welchen Graphen und Funktionsgleichungen es sich um lineares, quadratisches oder exponentielles Wachstum handelt.
TippsBei einem linearen Wachstum nimmt der Wert pro Zeiteinheit um denselben Summanden zu.
Zeichnen wir den Graphen zu einem quadratischen Wachstum, erhalten wir einen Teil einer Parabel.
Allgemein können wir die Funktionsgleichung für exponentielles Wachstum als $f(x)=c\cdot a^x$ mit $0<a$ als Wachstumsfaktor und $c$ als Anfangswert schreiben.
LösungWir vergleichen drei Wachstumsarten:
- Bei einem linearen Wachstum nimmt der Wert pro Zeiteinheit um denselben Summanden zu. Zeichnen wir den Graphen, erhalten wir eine Gerade mit konstanter Steigung. Allgemein können wir die Funktionsgleichung schreiben als $f(x)=mx+b$ mit $m$ als Steigung und $b$ als $y$-Achsenabschnitt. Für unseren Fall beschreibt $g(x)=50\cdot x$ eine Gerade durch den Ursprung $O(0,0)$, also ein lineares Wachstum.
- Bei einem quadratischen Wachstum nimmt der Wert mit dem Quadrat zu. Das heißt, dass wir hier die zweite Potenz des Arguments (meist mit $x$ bezeichnet) nehmen. Die Zunahme der Zunahme ist konstant. Zeichnen wir den Graphen, erhalten wir einen Teil einer Parabel. Allgemein können wir die Funktionsgleichung schreiben als $f(x)=a(x-d)^2+e$ mit $a$ als Streckungsfaktor und $d$ als $x$- und $e$ als $y$-Koordinate des Scheitelpunkts. Für unseren Fall beschreibt $h(x)=5\cdot x^2$ eine Parabel durch den Ursprung $O(0,0)$, also ein quadratisches Wachstum.
- Man spricht von exponentiellem Wachstum, wenn die prozentuale Zu- oder Abnahme pro Zeiteinheit und damit der Wachstumsfaktor konstant ist. Zeichnen wir den Graphen, erhalten wir einen Teil einer sogenannten $e$-Funktion. Allgemein können wir die Funktionsgleichung schreiben als $f(x)=c\cdot a^x$ mit $0<a$ als Basis und $c$ als Anfangswert. Für unseren Fall beschreibt $f(x)=2^x$ ein exponentielles Wachstum.
-
Ermittle die Basis der Exponentialfunktion.
TippsHaben wir eine Formel für exponentielles Wachstum von Bakterien gegeben:
- $f(x)=0,5 \cdot 3^x$
- $f(7)=0,5 \cdot 3^7= 1093,5$
LösungHier wollen wir so vorgehen:
- Die gegebenen Variablen einsetzen.
- Die Gleichung mit den eingesetzten Variablen nach der Basis $a$ umstellen.
- Mit Hilfe der Basis die Bakterienanzahl nach $2$ Stunden ausrechnen.
Wir nutzen die allgemeine Formel für exponentielles Wachstum mit $x$ für die Zeit in Stunden:
$f(x)=c \cdot a^x$
Wir wissen, dass der Anfangswert $c=100$ ist, also setzen wir diesen ein:
$f(x)=100 \cdot a^x$
Außerdem verdoppelt sich die Anzahl der Bakterien nach $15$ Minuten, also $\frac 14$ Stunde. Habe ich also am Anfang $100$ Bakterien, habe ich nach einer Viertelstunde zum Zeitpunkt $x=\frac14$ schon $200$ Bakterien.
Damit gilt:
$f(\frac14)=100 \cdot a^{\frac14}=100 \cdot 2=200$
Dies können wir nach $a$ umstellen, indem wir auf beiden Seiten durch $100$ teilen:
$a^{\frac14}$$=2$
Nehmen wir nun die vierte Potenz, gilt:
$(a^{\frac14})^4=a^{\frac{1\cdot 4}4}=a^1=a$
Somit erhalten wir:
$a=2^4=16$
Unser exponentielles Wachstum kann also mit $c=100$ und $a=16$ beschrieben werden durch:
$f(x)=c \cdot a^x=100 \cdot 16^x$
Wir setzen nun die $2$ Stunden ein und erhalten:
- $f(2)=100 \cdot 16^2= 100 \cdot 256= 25600$
9.718
sofaheld-Level
6.600
vorgefertigte
Vokabeln
8.281
Lernvideos
38.567
Übungen
33.604
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Klassenstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung


 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?