Exponentielle Wachstumsvorgänge


in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
Grundlagen zum Thema Exponentielle Wachstumsvorgänge
In diesem Video wird gezeigt, was exponentielles Wachstum ist und welche natürlichen Prozesse durch exponentielles Wachstum beschrieben werden können. Anhand eines Beispiels wird gezeigt, wie man den Graphen einer exponentiellen Wachstumsfunktion skizzieren kann und welche Form die Funktionsgleichung der Wachstumsfunktion hat.
Transkript Exponentielle Wachstumsvorgänge
Bakterienpopulationen wachsen durch Zellteilung. Die Zeit, die eine Zelle braucht, um sich zu teilen, nennt man Zellteilungsrate. Sie ist für verschiedene Bakterienarten unterschiedlich. Das Darmbakterium Escherichia coli benötigt für eine Teilung unter Laborbedingungen ca. 17 Minuten, das zur Käseherstellung verwendete Bakterium Lactococcus lactis dagegen 48 Minuten. Welche Mathematik steckt aber hinter der Käseherstellung? Die Antwort findest du in diesem Video.
Exponentielles Wachstum am Beispiel Bakterienproduktion
Die Frage ist also: Wie schnell wächst eine Bakterienpopulation, z.B. Lactococcus lactis, unter idealen Bedingungen? Um das herauszubekommen, kannst du eine Wertetabelle machen. In die erste Zeile trägst du die Zeitschritte ein, in die zweite Zeile die Zahl der Bakterien.
Es wird angenommen, dass zum Zeitpunkt Null nur ein Bakterium existiert. Nach dem ersten Zeitschritt, also nach 48 Minuten, erfolgt die erste Zellteilung. Jetzt existieren zwei Bakterien.
Nach weiteren 48 Minuten teilen sich diese zwei Organismen, so dass die Gesamtzahl der Bakterien auf vier steigt. Du siehst, dass sich die Population mit jedem Zeitschritt verdoppelt, da sich alle alle Bakterien jeweils einmal teilen.
Du füllst die Tabelle für fünf weitere Zeitschritte aus und siehst, dass nach 336 Minuten schon 128 Bakterien vorhanden sind. Mit Hilfe der Wertetabelle kann das Wachstum grafisch dargestellt werden.
Wenn du die Punkte in ein Diagramm einträgst und einen Funktionsgraphen hindurchlegst, ergibt sich die typische Form einer Exponentialfunktion. Mit der Exponentialfunktion kann man exponentielles Wachstum mathematisch beschreiben. Die allgemeine Funktionsgleichung lautet f(x)=cax. Dabei bezeichnet man c als Anfangswert und a als Wachstumsfaktor.
Der Anfangswert gibt an, welchen Wert die Größe zum Zeitpunkt x=0 hat. Im Beispiel ist der Anfangswert c=1, da zum Zeitpunkt x=0 ein Bakterium vorhanden ist.
Der Wachsumsfaktor gibt an, um welchen Faktor die Größe pro Zeiteinheit anwächst. Im Beispiel beträgt der Wachstumsfaktor rund 1,0145. Der Wachstumsfaktor ist beim exponentiellen Wachstum konstant. Vom Wachstumsfaktor a ist die Änderungsrate k zu unterscheiden.
Als Änderungsrate k bezeichnet man die absolute Änderung der Größe pro Zeiteinheit, also Delta N durch Delta t. Die Änderungsrate entspricht dabei der Steigung des Funktionsgraphen zum betrachteten Zeitpunkt. Beim linearen Wachstum ist die Änderungsrate k konstant. Pro Zeiteinheit erfolgt immer die gleiche Änderung der Größe.
Beim exponentiellen Wachstum dagegen ist die Änderungsrate nicht konstant, sondern proportional zur beobachteten Größe selbst. Das leuchtet am Beispiel der Bakterienpopulation ein: je mehr Bakterien vorhanden sind, desto mehr Bakterien können durch Teilung auch neu entstehen.
Die Änderungsrate zum Zeitpunkt t1 entspricht dem Anstieg der Tangente an den Funktionsgraphen zu diesem Zeitpunkt. Zum Zeitpunkt t_1 = 192 min beträgt die Änderungsrate k_1 = 0,23. Zum Zeitpunkt t_2 = 288 Minuten beträgt die Änderungsrate dagegen 0,92.
Zusammenfassung exponentielles Wachstum
Hier noch einmal eine Zusammenfassung: exponentielles Wachstum beschreibt das Wachstum einer Größe, wenn die Geschwindigkeit des Wachstums proportional zur Größe selbst ist. Das ist bei vielen natürlichen Prozessen der Fall, z.B. bei der Vermehrung von Organismen.
Aber auch die Entwicklung eines verzinsten Sparguthabens auf dem Bankkonto kann durch exponentielles Wachstum beschrieben werden. Das exponentielle Wachstum wird durch die allgemeine Gleichung f(x)=cax beschrieben. c bezeichnet den Anfangswert und a den Wachstumsfaktor. Der Wachsumsfaktor ist eine Konstante und gibt das relative Wachstum pro Zeiteinheit an. Das absolute Wachstum pro Zeiteinheit, die Änderunsrate k, ist beim exponentiellen Wachstum nicht konstant.
Hättest du gedacht, dass im Käse soviel Mathematik steckt? Vielleicht findest du ja in deiner Umgebung noch mehr Dinge, denen exponentielles Wachstum zugrunde liegt. Viel Spaß dabei!
Exponentielle Wachstumsvorgänge Übung
-
Gib die allgemeine Form einer exponentiellen Wachstumsfunktion an und beschreibe die einzelnen Parameter.
TippsDie Variable $x$ steht in der Basis und wird potenziert: $f(x)=x^n$. Dies ist eine Potenzfunktion.
Bei der Funktion $f(x)=a^x$ steht die Variable im Exponenten.
Zum Zeitpunkt $0$, also am Anfang der Untersuchung, ist $f(0)=c\cdot a^0=c$.
LösungExponentielles Wachstum, welches auch als unbegrenztes exponentielles Wachstum bezeichnet wird, liegt vor, wenn sich eine Größe in jeweils gleichen Zeitabschnitten immer um denselben Faktor verändert.
Ein solches Wachstum kann in Form einer Exponentialfunktion beschrieben werden. Dies ist eine Funktion der Form
$f(x)=c\cdot a^x$.
Folgende Eigenschaften treffen zu:
- $x$ ist die unabhängige Variable und steht im Exponenten.
- $a\in \mathbb{R}^+$ ist die Basis der Exponentialfunktion.
- $c\in \mathbb{R}$ ist eine Konstante. Diese steht für den Anfangswert bei exponentiellen Prozessen.
-
Ergänze die Wertetabelle für die Lactococcus lactis-Bakterien.
TippsDer Anfang entspricht Zeit gleich $0$.
Bei einer Zellteilung teilt sich eine Zelle immer in zwei Zellen.
Die Anzahl der Zellen wird also immer verdoppelt.
Alle Einträge sind Zweierpotenzen.
LösungHier ist die komplette Wertetabelle zu sehen:
- Am Anfang gibt es ein Bakterium. Also steht bei der Zeit $0$ die Anzahl $1$.
- nach $48$ Minuten gibt es zwei Bakterien,
- nach $96$ Minuten $2\cdot 2=4$ Bakterien,
- nach $144$ Minuten $2\cdot 4=8$ Bakterien und
- nach $196$ Minuten $2\cdot 8=16$ Bakterien.
-
Stelle die Wachstumsfunktion für die mit Seerosen bedeckte Fläche auf.
Tipps$c$ ist der Anfangswert, also der Wert zu $x=0$.
Du weißt, dass $f(2)=9$ ist.
Löse bei bekanntem $c$ die Gleichung
$c\cdot a^{2}=9$.
Die Basis muss größer als $1$ sein.
Insbesondere darf sie natürlich nicht negativ sein.
LösungDurch die Wachstumsfunktion wird die Veränderung der von Seerosen bedeckten Fläche nach $x$ Tagen angegeben.
Am Anfang, also bei $x=0$, bedecken die Seerosen $4~m^2$. Mit dieser Information können wir schon folgende Gleichung aufstellen:
$4=f(0)=c\cdot a^0=c$
Somit ist $c=4$. Das kann man sich auch dadurch klarmachen, dass $c$ der Anfangswert ist.
Nun kann man sich den Wachstumsfaktor anschauen. Es gilt $f(2)=9$. Dies führt zu der Gleichung $4\cdot a^{2}=9$. Wir lösen diese Gleichung nach $a$ auf, indem wir zuerst durch $4$ dividieren und dann die Wurzel ziehen. Wir erhalten $a=1,5$.
Die gesuchte Funktion lautet somit $f(x)=4\cdot 1,5^x$.
-
Gib die Funktion an, welche die Entwicklung von Pauls gespartem Geld beschreibt.
TippsDer Anfangswert ist das Guthaben, welches Paul anlegt.
Bekannt ist die Wachstumsrate $p=2,5~\%$.
Bei bekannter Wachstumsrate $p$ erhältst du den Wachstumsfaktor so
$a=1+\frac{p}{100}$.
Beachte, dass $a>1$ sein muss.
LösungPaul überlegt, wie er das Anwachsen seines Guthabens als exponentielle Wachstumsfunktion der Form $f(x)=c\cdot a^x$ aufschreiben kann.
In der Wachstumsfunktion steht
- $x$ für die Zeit in Jahren,
- $f(x)$ für das angesparte Guthaben nach $x$ Jahren,
- $c$ für den Anfangswert und
- $a>1$ für den Wachstumsfaktor.
Die Wachstumsrate $p=2,5~\%$ ist bekannt. Damit kann der Wachstumsfaktor
$a=1+\frac{p}{100}=1,025$
berechnet werden. Die gesuchte Funktion ist somit
$f(x)=3000\cdot 1,025^x$.
-
Beschreibe, wie eine Exponentialfunktion verläuft.
TippsDer Graph einer linearen Funktion ist eine Gerade.
Der Graph einer quadratischen Funktion ist eine Parabel.
Sowohl eine lineare als auch eine quadratische Funktion sind Polynomfunktionen. In diesen steht die Variable in der Basis.
In einer Exponentialfunktion steht die Variable im Exponenten.
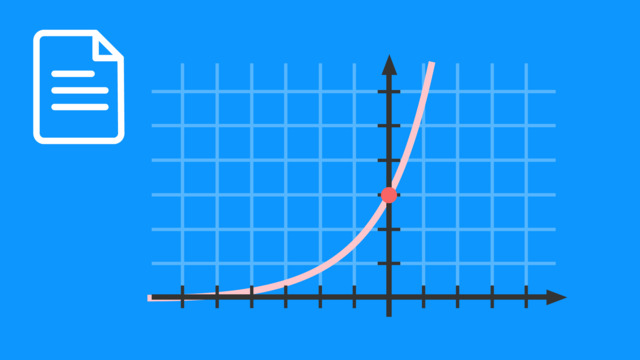
Stelle dir beim Funktionsgraphen einer exponentiellen Wachstumsfunktion ein startendes Flugzeug vor.
LösungHier ist der übliche Verlauf einer exponentiellen Wachstumsfunktion zu sehen.
Man kann sich dies so vorstellen wie ein startendes Flugzeug.
Je nach der Basis $a$ steigt diese Funktion steiler oder weniger steil an.
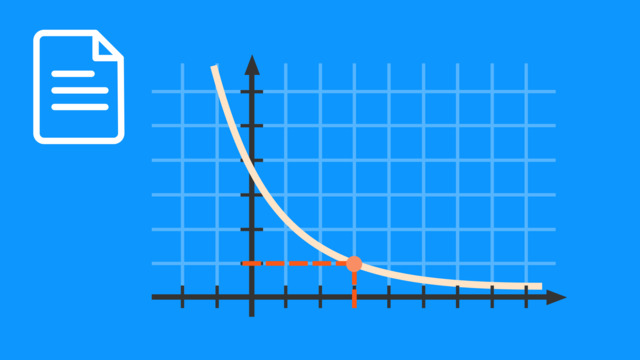
Im Falle einer exponentiellen Abnahmefunktion ($0<a<1$) wird der Graph an der y-Achse gespiegelt.
-
Berechne, wie hoch das Guthaben nach einer gegebenen Zeit ist, sowie die Zeit, die vergeht, bis das Guthaben eine gewisse Höhe erreicht hat.
TippsDer jeweilige Geldbetrag wird auf zwei Stellen nach dem Komma gerundet.
Wenn du die Zahl der Jahre kennst, setzt du diese in die Funktionsgleichung ein.
Wenn du die Anzahl der Jahre suchst, musst du entweder probieren oder du verwendest den Logarithmus.
Schaue dir das folgende Beispiel an: Wann ist das Guthaben auf $3655,21~€$ angewachsen?
Es muss also die Gleichung $3655,21=3000\cdot 1,025^x$ gelöst werden.
Dies kannst du hier sehen.
Lösung- Entweder ist die Zeit $x$ bekannt und das Guthaben $f(x)$ gesucht oder
- das Guthaben $f(x)$ bekannt und die Zeit ist gesucht.
- $f(5)=3000\cdot 1,025^5\approx 3394,22$
- $f(10)=3000\cdot 1,025^{10}\approx 3840,25$
Das Guthaben $3479,08~€$ ist bekannt:
$\begin{array}{rclll} 3479,08&=&3000\cdot 1,025^x&|&:3000\\ 1,1597&=&1,025^x&|&\ln(~~~)\\ \ln(1,1597)&=&x\cdot \ln(1,025)&|&:\ln(1,025)\\ x&=&\frac{\ln(1,1597)}{\ln(1,025)}\approx 6 \end{array}$
Das bedeutet, dass nach sechs Jahren das Guthaben auf den gegebenen Betrag angewachsen ist.
Ebenso kann die Zeit berechnet werden, nach der das Guthaben auf $4344,89~€$ angewachsen ist. Dies führt zu $x=15$.
9.782
sofaheld-Level
6.600
vorgefertigte
Vokabeln
8.298
Lernvideos
38.617
Übungen
33.652
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Klassenstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung




 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?














Ich schreibe als Elternteil für meinen Sohn, der Wachstumsfaktor wird ohne jede Erklärung genannt....a ist 1,014..... hier fehlt eine wichtige Information.
Wie man auf den Wachstumsfaktor kommt ist mir leider noch unklar :(
Der schritt von der Wertetabelle zum Wachstumsfaktor wir komplett übersprungen. Das ist schade, denn bis dahin war alles sehr anschulich
Sehr gutes Video :) Vor allem Biologie und Mathe zu verbinden finde ich toll. Bitte mehr davon :D