Exponentialfunktion – Funktionsgleichung bestimmen


in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
Grundlagen zum Thema Exponentialfunktion – Funktionsgleichung bestimmen
Nach dem Schauen dieses Videos wirst du in der Lage sein, die Funktionsgleichung einfacher Exponentialfunktionen anhand gegebener Punkte aufzustellen.
Zunächst lernst du, warum man für einige Exponentialfunktionen nur einen einzigen Punkt braucht, um die Funktionsgleichung eindeutig bestimmen zu können. Anschließend schauen wir uns einige Bespielaufgaben gemeinsam an. Abschließend erfährst du, wie du Funktionsgleichungen von Exponentialfunktionen mit Streckfaktor aufstellen kannst.

Das Video beinhaltet Schlüsselbegriffe, Bezeichnungen und Fachbegriffe wie Exponentialfunktion, Basis, Vorfaktor (Streckfaktor), Potenz, Exponent, Wurzel.
Bevor du dieses Video schaust, solltest du bereits die Grundlagen zu Exponentialfunktionen kennen und sicher mit Gleichungsumformungen und Potenzgesetze umgehen können Außerdem solltest du grundlegendes Wissen zur Bestimmung von Funktionsgleichungen (zum Beispiel bei linearen Funktionen) haben.
Transkript Exponentialfunktion – Funktionsgleichung bestimmen
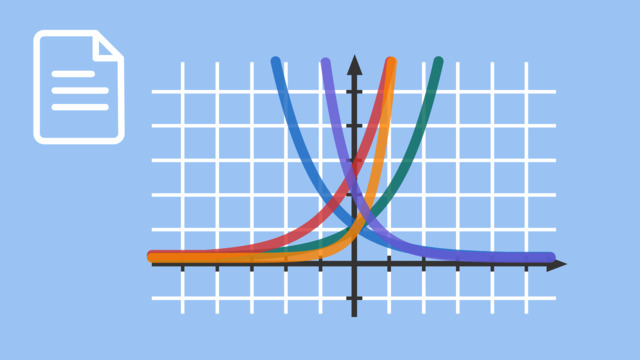
Kennst du das, wenn du total Hunger hast, aber der Kühlschrank leer ist? Alles was noch übrig ist, ist eine Packung Eier. Hm, ob man mit einer einzigen Zutat überhaupt irgendwas kochen kann, das satt macht? Und kann man eigentlich aus einem einzigen Punkt die Gleichung einer Funktion bestimmen? „Bei Exponentialfunktionen geht das! Wie? Das schauen wir uns einmal genauer an.“ Normalerweise braucht man zum Beispiel bei linearen Funktionen zwei Punkte, um den Anstieg zu ermitteln. Bei Parabeln braucht man sogar drei Punkte, um die Funktionsgleichung eindeutig zu bestimmen. Und bei Exponentialfunktionen reicht plötzlich nur ein Punkt? Das würde bedeuten, dass keine andere Exponentialfunktion durch diesen Punkt geht und die Funktion dadurch eindeutig zugeordnet werden kann. Und tatsächlich. Die Exponentialfunktionen der Form „a hoch x“ fächern sich alle so auf, dass sie einander nirgendwo schneiden, mit Ausnahme eines einzigen Punktes: Alle Exponentialfunktionen dieser Form gehen durch den Punkt P „null, eins“. Ist die Basis a größer als eins, verlaufen die Exponentialfunktionen streng monoton steigend. Ist a dagegen kleiner als eins, ist der Verlauf streng monoton fallend. Na dann schauen wir mal, wie die Funktionsgleichung der Exponentialfunktion lautet, auf der der Punkt „eins, zwei“ liegt. Was wir schon einmal sagen können, ist, dass die Basis größer als eins sein muss. Dann setzen wir den x-Wert und den y-Wert in die Funktionsgleichung ein. Die Basis der Exponentialfunktion ist also zwei. Der Punkt liegt somit auf der Exponentialfunktion „zwei hoch x“. Wenn wir Kommazahlen als Koordinaten haben, gehen wir genauso vor. Wir setzen erst einmal die Koordinaten ein. Anschließend müssen wir beide Seiten hoch Ein-Drittel nehmen, was ja gleichbedeutend mit dem Ziehen der dritten Wurzel ist. So können wir den Parameter a berechnen, und wissen, dass der Punkt P auf der Exponentialfunktion „0,6 hoch x“ liegt. Dass die Basis kleiner als eins sein muss, können wir auch erkennen, wenn wir uns die Exponentialfunktionen noch einmal im Koordinatensystem anschauen. Durch den Punkt P muss eine monoton fallende Funktion verlaufen. Wir können uns also merken: wenn der gegebene Punkt hier oder hier liegt, ist der Funktionsverlauf streng monoton steigend, also muss die Basis a größer als eins sein. Liegt der Punkt jedoch in diesen Bereichen, handelt es sich um eine monoton fallende Exponentialfunktion und die Basis a muss kleiner als eins sein. Haben wir jedoch den Punkt „null, eins“ gegeben, können wir keine Basis bestimmen, weil alle Exponentialfunktionen der Form „a hoch x“ durch diesen Punkt verlaufen. Wenn Exponentialfunktionen auch einen Streckfaktor b haben, müssen zwei Punkte des Graphen gegeben sein, um die Funktionsgleichung eindeutig zu bestimmen. Das heißt, wir müssen hier zwei Gleichungen aufstellen. Für die erste Gleichung erhalten wir zwei, wenn wir für x eins einsetzen. Und bei der zweiten Gleichung erhalten wir 0,25, wenn wir für x vier einsetzen. Nun lösen wir eine der beiden Gleichungen nach b auf - wir nehmen dafür die erste. Wir teilen also durch a hoch eins, dann steht das b isoliert auf der rechten Seite. Damit können wir praktischerweise das Einsetzungsverfahren nutzen und setzen die nach b umgestellte Gleichung für das b in die zweite Gleichung ein. Den Term, den wir dann erhalten, können wir noch umformen. „a hoch vier“ durch „a hoch eins“ sind „a hoch drei“. Dann stellen wir nach a um, rechnen „hoch ein Drittel“, und erhalten „a gleich 0,5“. Jetzt müssen wir noch den Streckfaktor b bestimmen. Dazu setzen wir das Ergebnis für a in die nach b umgestellte Gleichung ein, und erhalten „b gleich vier“. Durch die Punkte P und Q verläuft also die Funktion „vier mal 0,5 hoch x“. Besonders einfach wird es übrigens, wenn wir die Punkte bei „x gleich null“ und „x gleich eins“ gegeben haben. Das sehen wir, wenn wir diese beiden x-Werte in die Funktionsgleichung einsetzen. Bei der ersten Funktionsgleichung ist „a hoch null“ gleich eins, deshalb ist b gleich fünf. Das heißt, wenn die x-Koordinate null ist, verrät uns die y-Koordinate direkt den Wert für b. In der zweiten Gleichung erhalten wir fünfzehn gleich „b mal a“, somit ist a gleich drei. Wenn also die x-Koordinate eins ist, ist die y-Koordinate das Produkt aus a und b. Mit diesen beiden günstig gelegenen Punkten können wir also ganz schnell die Funktionsgleichung aufstellen. Alles klar, dann bringen wir das Ganze nochmal auf den Punkt. Um die Funktionsgleichung von Exponentialfunktionen der Form „a hoch x“ zu bestimmen, genügt ein einziger Punkt. Wenn du den Punkt im Koordinatensystem verortest, kannst du auch direkt schon abschätzen, ob die Basis a größer oder kleiner als eins ist. Einzige Ausnahme: Es darf nicht der Punkt „null, eins“ sein. Bei Funktionen der Form „b mal a hoch x“ brauchen wir zwei Punkte. Besonders einfach wird es, wenn es sich dabei um Punkte mit den x-Koordinaten Null und eins handelt. Ist es nicht faszinierend, dass ein einziger Punkt einen kompletten Funktionsverlauf bestimmen kann? Und auch aus einer einzigen Zutat kann man ein köstliches Menü zaubern.
Exponentialfunktion – Funktionsgleichung bestimmen Übung
-
Gib an, wie die Funktionsgleichung einer Exponentialfunktion bestimmt werden kann.
TippsWelchen Punkt haben diese Exponentialfunktionen der Form $f(x) = a^x$ gemeinsam und wie lassen sie sich voneinander unterscheiden?
Zur Bestimmung der beiden Parameter in einer Exponentialfunktion der Form $f(x) = b \cdot a^x$ benötigst du zwei Gleichungen.
LösungDie Exponentialfunktionen der Form $f(x)=a^x$ fächern sich so auf, dass sie einander nirgendwo schneiden mit Ausnahme eines einzigen Punktes $P(1\vert0)$. Daher kann man die Funktionsgleichung für diese Exponentialfunktion mit nur einem weiteren Punkt eindeutig bestimmen.
Wenn Exponentialfunktionen einen Faktor $b$ enthalten, dann müssen zwei Punkte gegeben sein, um die beiden Parameter in der Funktionsgleichung $f(x) = b \cdot a^x$ eindeutig zu bestimmen.
Folgende Aussagen sind korrekt:
- Um eine Funktionsgleichung der Form $f(x)=b\cdot{a}^x$ zu bestimmen, benötigt man zwei beliebige Punkte der Funktion.
- Um eine Funktionsgleichung der Form $f(x)=a^x$ zu bestimmen, benötigt man einen beliebigen Punkt der Funktion außer $P(1\vert0)$.
- Um eine Funktionsgleichung der Form $f(x)=a^x$ zu bestimmen, benötigt man den Punkt $P(1\vert0)$.
- Um eine Funktionsgleichung der Form $f(x)=b\cdot{a}^x$ zu bestimmen, benötigt man den Punkt $P(1\vert0)$ und einen weiteren beliebigen Punkt der Funktion.
-
Beschreibe, wie die Monotonie einer Exponentialfunktion $f(x) = a^x$ abgelesen werden kann.
TippsDieser Graph ist streng monoton steigend.
Alle Exponentialfunktionen der Form $f(x) = a^x$ gehen durch den Punkt $(0 \vert 1)$. Der Parameter $a$ gibt an, ob die Funktionswerte zu oder abnehmen.
Beispiele:
- $a = 5$: $f(1) = 5^1 = 5 \Rightarrow$ Die Werte nehmen zu.
- $a = 0{,}2$: $f(1) = 0{,}2^1 = 0{,}2 \Rightarrow$ Die Werte nehmen ab.
LösungUm herauszufinden, welche Monotonie (also welchen Verlauf in dem Koordinatensystem) die Funktion annimmt, schaust du dir die Basis $a$ an. Streng monoton steigend bedeutet, dass die Funktionswerte immer zunehmen, der Graph hat eine positive Steigung. Streng monoton fallend bedeutet, dass die Funktionswerte immer abnehmen, der Graph hat eine negative Steigung.
Für Exponentialfunktionen der Form $f(x) = a^x$ gilt:
Wenn du einen Punkt der Funktion im Koordinatensystem verortest, kannst du direkt abschätzen, ob die Basis $a$ größer oder kleiner als $\mathbf{1}$ ist. Befindet sich der Punkt im lilanen Bereich, ist $a$ größer als $1$. Liegt der Punkt im grünen Bereich, ist $a$ kleiner als $1$.Ist die Basis $a$ größer als $1$, verläuft die Exponentialfunktion streng monoton steigend. Ist $a$ dagegen kleiner als $1$, ist der Verlauf streng monoton fallend.
Auch bei Exponentialfunktionen der Form $f(x) = b \cdot a^x$ gilt das Kriterium:
- $a \gt 1 \quad \Rightarrow \quad$ streng monoton steigend
- $a \lt 1 \quad \Rightarrow \quad$ streng monoton fallend
-
Bestimme die Funktionsgleichung der Exponentialfunktion.
TippsDie gegebenen Punkte kannst du in die allgemeine Formel einsetzen.
Beispiel:
$R(2 \vert 4)$ in $f(x) = b \cdot a^x$
$4 = b \cdot a^2$Wenn du einen Punkt mit $x$-Wert $1$ vorliegen hast, kannst du den Streckfaktor $b$ direkt ablesen. Diesen setzt du dann in die zweite Gleichung ein.
LösungDen Funktionsterm einer Exponentialfunktion kannst du bestimmen, indem du die Koordinaten zweiter Punkte in die allgemeine Funktionsgleichung $f(x) = b \cdot a^x$ einsetzt und die beiden Parameter $a$ und $b$ berechnest.
Besonders einfach ist die Funktionsgleichung von Exponentialfunktionen zu bestimmen, wenn bei einem der Punkte $x=0$ ist. Dann kannst du $b$ direkt aus der $y$-Koordinate ablesen. Es gilt: $(0 \vert b)$, da $f(0) = b \cdot a^0 = b$.
$P(0\vert7) ~ \rightarrow ~ 7 = b \cdot a^0 = b \cdot 1 = b$
Hier ist also $b=7$.Dann setzt du $b=7$ in die Gleichung ein, die du mit dem zweiten Punkt $Q(1\vert21)$ aufstellen kannst, also
$\begin{array}{rcll} f(x) &=& b \cdot a^x \\ \rightarrow ~ 21 &=& 7 \cdot a^1 & \vert : 7 \\ \dfrac{21}{7} &=& a \\ \implies a &=& 3 \end{array}$
Für einen gegebenen Punkt mit $x$-Koordinate $1$ gilt allgemein: $(1 \vert a \cdot b)$, da $f(1) = b \cdot a^1 = a \cdot b$.
Die Funktionsgleichung lautet dann:
$f(x)=7 \cdot 3^x$ -
Ermittle die Monotonie der Exponentialfunktionen.
TippsOb der Graph einer Exponentialfunktion mit der Gleichung $f(x) = b \cdot a^x$ steigt oder fällt, hängt nur von der Basis $a$ ab.
Der Graph zeigt die Funktion $f(x) = 0{,}9 \cdot 2^x$.
Er ist streng monoton steigend.Der Graph zeigt die Funktion $f(x) = 2 \cdot 0{,}5^x$.
Er ist streng monoton fallend.LösungDer Graph einer Exponentialfunktion hat stets im gesamten Definitionsbereich ein gleichbleibendes Monotonieverhalten. Er ist streng monoton steigend oder streng monoton fallend. Ob der Graph einer Funktion mit der Gleichung $f(x) = b \cdot a^x$ steigt oder fällt, hängt dabei nur von der Basis $a$ ab.
Es gilt:- $a \gt 1 \quad \Rightarrow \quad$ Der Graph ist streng monoton steigend.
- $a \lt 1 \quad \Rightarrow \quad$ Der Graph ist streng monoton fallend.
Zu „streng monoton steigend“ ordnest du alle Funktionen zu, deren Basis $a$ größer $1$ ist. Den Streckfaktor $b$ brauchst du dabei nicht berücksichtigen.
Monoton steigende Funktionen sind:
- $f(x)=0{,}4 \cdot 5^x~\rightarrow~a=5 \gt 1$
- $f(x)=\frac{1}{4} \cdot 3^x~\rightarrow~a=3 \gt 1$
- $f(x)=2 \cdot 6^x~\rightarrow~a=6 \gt 1$
Zu „streng monoton fallend“ ordnest du alle Funktionen zu, deren Basis $a$ kleiner $1$ ist. Den Streckfaktor $b$ brauchst du dabei nicht berücksichtigen.
Monoton fallende Funktionen sind:
- $f(x)=0{,}5 \cdot 0{,}5^x~\rightarrow~a=0{,}5 \lt 1$
- $f(x)=\frac{1}{5} \cdot 0{,}2^x~\rightarrow~a=0{,}2 \lt 1$
- $f(x)=4 \cdot \left(\frac{1}{10}\right)^x~\rightarrow~a= \frac{1}{10} \lt 1$
-
Vervollständige die Gleichung der Exponentialfunktion.
TippsBeispiel: Wenn wir den Punkt $P(2\vert3)$ in $f(x)=a^x$ einsetzen, erhalten wir $a^2=4$.
Beachte:
Wenn $a$ größer $1$ ist, ist die Funktion streng monoton steigend.
Wenn $a$ kleiner $1$ ist, ist die Funktion streng monoton fallend.LösungUm die Funktionsgleichung einer Exponentialfunktion eindeutig zu bestimmen, benötigst du nur einen beliebigen Punkt, durch den sich der Funktionsgraph von den anderen Graphen unterscheidet. Da alle Funktionsgraphen von Exponentialfunktionen der Form $f(x) = a^x$ durch den Punkt $P(0 \vert 1)$ gehen, ist dieser Punkt nicht geeignet. Wenn ein geeigneter Punkt gegeben ist, kannst du den $x$-Wert in die Funktionsgleichung $f(x)=a^x$ einsetzen und erhältst durch Lösen der Gleichung den Wert für $a$.
Die Funktionsgleichung wird wie folgt berechnet:
$P(1\vert2)$ wird in $f(x) = a^x$ eingesetzt:
$\begin{array}{rrcl} & f(1) &=& a^1 = 2\\ \implies & a &=& 2 \\ \implies & f(x) &=& 2^x \\ \end{array}$
Der Graph der Exponentialfunktion ist streng monoton steigend, da $a = 2 \gt 1$.
-
Stelle die Funktionsgleichung der Exponentialfunktion auf, die durch die Punkte $P$ und $Q$ verläuft.
TippsDa die Gleichung $f(x)=b \cdot a^x$ zwei Unbekannte $a$ und $b$ enthält, benötigst du zwei Gleichungen, die du mit den gegebenen Punkten aufstellen kannst.
Um die unbekannten Variablen zu berechnen, löst du eine Gleichung nach $b$ auf und setzt den so berechneten Term für $b$ dann in die zweite Gleichung ein.
LösungUm die Gleichung einer Exponentialfunktion der Form $f(x)=b \cdot a^x$ zu bestimmen, benötigst du zwei beliebige Punkte, durch die der Funktionsgraph verläuft.
1. Beispiel: $P(1\vert5)$ und $Q(0\vert10)$
- $Q$ einsetzen: $10 = b \cdot a^0 ~ \Rightarrow ~ b = 10$
- $b$ und $P$ einsetzen: $5 = 10 \cdot a^1 ~ \Rightarrow ~ a = 0{,}5$
2. Beispiel: $P(2\vert3{,}2)$ und $Q(-1\vert0{,}05)$
- $P$ einsetzen: $ 3{,}2 = b \cdot a^2 ~ \Rightarrow ~ b = \frac{3{,}2}{a^2}$
- $b$ und $Q$ einsetzen: $0{,}05 = \frac{3{,}2}{a^2} \cdot a^{-1} ~ \Rightarrow ~ a^3 = \frac{3{,}2}{0{,}05} ~ \Rightarrow ~ a = 4$
- $b = \frac{3{,}2}{4^2} = 0{,}2$
3. Beispiel: $P(1\vert3)$ und $Q(6\vert0{,}5)$
- $P$ einsetzen: $ 3 = b \cdot a^1 ~ \Rightarrow ~ b = \frac{3}{a}$
- $b$ und $Q$ einsetzen: $0{,}5 = \frac{3}{a} \cdot a^{6} ~ \Rightarrow ~ a^5 = \frac{0{,}5}{3} ~ \Rightarrow ~ a \approx 0{,}7$
- $b = \frac{3}{0{,}7} \approx 4{,}3$
9.711
sofaheld-Level
6.600
vorgefertigte
Vokabeln
8.342
Lernvideos
38.729
Übungen
33.706
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Klassenstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung







 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?














Danke für den Hinweis! Wir haben es korrigiert, liebe Grüße aus der Redaktion!
Das Video ist toll. Leider ist bei Übung 1 ein Fehler. Der Punkt (1/0) liegt nicht auf der Exponentialfunktion. Gemeint ist vermutlich der Punkt (0/1).
Danke für die Mühe.