Exponentialfunktion – Definition


in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
Grundlagen zum Thema Exponentialfunktion – Definition
Nach dem Schauen dieses Videos wirst du die Definition und die wichtigsten Eigenschaften von Exponentialfunktionen kennen.

Zunächst wird der Verlauf einiger Funktionen anhand ihrer Wertetabellen untersucht. Anschließend schauen wir uns die Eigenschaften wie Monotonieverhalten, Definitions- und Wertebereich an. Abschließend lernst du, wie die Funktionen an der y-Achse gespiegelt werden.
Lerne außerdem etwas über die Entwicklung des Bevölkerungswachstums.

Das Video beinhaltet Schlüsselbegriffe, Bezeichnungen und Fachbegriffe wie Basis, Exponent, Potenz, Monotonie, Spiegelung, Definitionsbereich, Wertebereich, Asymptote und Nullstelle.
Nach diesem Video wirst du darauf vorbereitet sein, Weiteres zu Exponentialfunktionen und ihren Parametern zu lernen.
Transkript Exponentialfunktion – Definition
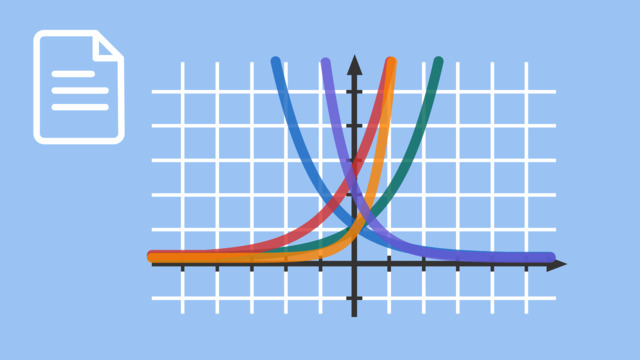
Wusstest du, dass es im Jahre null nur zweihundert Millionen Menschen auf der Erde gab? In den darauffolgenden tausend Jahren ist auch nicht viel passiert. Es hat bis zum im achtzehnten Jahrhundert gedauert, bis es eine Milliarde Menschen gab. Aber danach wurde das Bevölkerungswachstum immer rasanter. Um Neunzehnhundert waren es schon anderthalb Milliarden. Und nach nur sechzig Jahren hatte sich diese Anzahl bereits verdoppelt. Weitere sechzig Jahre später sind wir schon bei fast acht Milliarden angelangt. Wenn wir diese Werte in ein Koordinatensystem eintragen, erkennen wir, dass sich dieses schnelle Wachstum am besten mit „Exponentialfunktionen“ modellieren lässt. Was genau versteht man unter diesem Funktionstyp? Exponentialfunktionen haben eine positive reelle Zahl a als Basis. Anders als bei bisherigen Funktionen steht die Variable nämlich hier im Exponenten. Dadurch nimmt der Funktionswert mit jedem x-Wert eine andere Potenz zur Basis an. Wenn die Basis zum Beispiel zwei ist, bedeutet das dass sich der Funktionswert bei jedem Schritt verdoppelt. Bei der Funktion „drei hoch x“ verdreifacht sich der Funktionswert bei jedem Schritt. An der Stelle „x gleich null“ haben alle Exponentialfunktionen den gleichen Funktionswert, nämlich eins. Bei negativen x-Werten verkleinern sich die Funktionswerte und nähern sich immer mehr der Null an. Und so sehen die beiden Funktionsgraphen aus. Je größer außerdem die Basis ist, desto steiler verläuft der Funktionsgraph. Ist die Basis kleiner als eins, fällt der Funktionsgraph. Zum Beispiel die Funktionen „ein Halb hoch x“ oder „ein Drittel hoch x“. Das können wir mithilfe einer Wertetabelle nachweisen. Je größer die Exponenten, also die x-Werte werden, desto kleiner werden die Funktionswerte. Und je kleiner die Exponenten werden, desto größer sind die Funktionswerte. Auch für diese Funktionen gilt, dass bei „x gleich null“ der Funktionswert wieder eins ist. Gut, soweit also zu dem Fall a kleiner eins. Was würde passieren, wenn a genau eins ist? Dann wären alle Funktionswerte eins, denn egal mit welcher Zahl eins potenziert wird, eins mal eins mal eins ergibt immer eins. Wir hätten also eine Gerade, die waagerecht auf der Höhe eins verläuft. Das ist doch nun wirklich keine Exponentialfunktion! Deshalb ist die Basis eins in der Definition ausgenommen. Wenn wir nun alle Funktionsgraphen betrachten, können wir noch einmal deutlich erkennen, dass bei einer Basis größer als eins, der zugehörige Graph streng monoton steigend ist, während bei einer Basis kleiner als eins der Graph streng monoton fallend verläuft. Was erkennen wir noch? Die Funktionsgraphen haben einen einzigen gemeinsamen Punkt. Sie alle schneiden die y-Achse im Punkt „null eins“. Das liegt daran, dass jede beliebige Zahl „hoch null“ immer eins ergibt. Was können wir zum Definitions- und Wertebereich sagen? Nun, es können alle reellen Zahlen für x eingesetzt werden, da die Funktionen von minus unendlich bis plus unendlich durchgehend sind. Zu den Funktionswerten gehören nur die positiven, reellen Zahlen. „y gleich null“ wird zwar angenähert, aber nie erreicht. Das erkennt man daran, dass sich die Funktionen mit der Basis größer als eins für „x gegen minus unendlich“ immer weiter der x-Achse annähern, aber sie nie erreichen werden. Für die Funktionen mit einer Basis kleiner eins nähern sich die Graphen für „x gegen plus unendlich“ immer mehr der x-Achse an. Die x-Achse ist in diesem Fall die Asymptote der Exponentialfunktionen. Deshalb sagt man auch, die Funktionsgraphen nähern sich asymptotisch der x-Achse an, werden sie aber nie berühren oder schneiden. Da alle Funktionswerte positiv sind, haben die Exponentialfunktionen keine Nullstelle. Die letzte interessante Erkenntnis, die wir hier ansprechen wollen, ist der symmetrische Verlauf von je zwei Funktionsgraphen. Wenn wir zum Beispiel den Funktionsgraphen „zwei hoch x“ an der y-Achse spiegeln, erhalten wir den Graphen der Funktion „ein Halb hoch x“. Und wenn wir den Funktionsgraphen von „ein Drittel hoch x“ an der y-Achse spiegeln, erhalten wir den Graphen von „drei hoch x“. Man kann also allgemein sagen, dass die Graphen der Exponentialfunktionen „a hoch x“ und „eins durch a hoch x“ durch Spiegelung an der y-Achse auseinander hervorgehen. Statt „eins durch a hoch x“ kann man übrigens auch „a hoch minus x“ schreiben. So, das war nun aber genug Input zu Exponentialfunktionen. Wir fassen die wichtigsten Informationen noch einmal zusammen. Eine Funktion mit der Gleichung „f von x gleich a hoch x“ heißt Exponentialfunktion. Die Basis a ist dabei eine positive reelle Zahl und darf außerdem nicht eins sein. Der Definitionsbereich umfasst alle der Wertebereich nur die positiven reellen Zahlen. Das heißt, die Funktionsgraphen verlaufen oberhalb der x-Achse und haben somit auch keine Nullstelle. Außerdem schneiden alle Graphen die y-Achse im Punkt null eins. Ist die Basis größer als eins, ist der Funktionsgraph streng monoton steigend. Ist die Basis kleiner als eins, ist der Funktionsgraph streng monoton fallend. Alle Graphen nähern sich außerdem asymptotisch der x-Achse an. Bei „a größer als 1“ für „x gegen minus unendlich“ und bei „a kleiner eins“ für „x gegen unendlich“. Und wird die Weltbevölkerung nun immer weiter exponentiell anwachsen? Nun, die meisten Forscher*innen gehen nicht davon aus. Aber wahrscheinlich müssen wir in Zukunft trotzdem ein bisschen zusammenrutschen.
Exponentialfunktion – Definition Übung
-
Gib die Definition einer Exponentialfunktion an.
TippsEin Beispiel für exponentielles Wachstum ist:
${f{(x)}=2^x}$
Der Funktionswert verdoppelt sich bei jedem Schritt, also
$\begin{array}{c|c} f{(x)}=a^x & f{(x)}=2^x\\ \hline a^1 & 2\\ a^2 & 4\\ a^3 & 8\\ a^4 & 16\\ \end{array}$
LösungWas genau versteht man unter einer Exponentialfunktion?
Die Funktionsgleichung einer Exponentialfunktion hat allgemein die Form:
$f(x)=a^x$Die Variable $x$ steht hier, anders als beispielsweise bei ganzrationalen Funktionen, im Exponenten. Die Basis $a$ ist eine positive reelle Zahl. Die Funktion besteht also aus einer Potenz mit konstanter Basis und variablem Exponenten.
Ist wie bei $f_1$ und $f_2$ in der Darstellung $a>1$, so gilt:
- Der Funktionswert vergrößert sich mit jedem Schritt um den Faktor $a$.
$\begin{array}{c|c} f{(x)}=a^x & f{(x)}=2^x\\ \hline a^1 & 2\\ a^2 & 4\\ a^3 & 8\\ a^4 & 16\\ \end{array}$
Bei der Funktion $3^x$ verdreifacht sich der Funktionswert bei jedem Schritt.
- Für negative $x$-Werte werden die Funktionswerte immer kleiner und nähern sich für $x \to - \infty$ der Null an.
-
Beschreibe das Verhalten der Funktionsgraphen von Exponentialfunktionen.
TippsBeispiel:
Bei der Funktion $ f(x) = 4^x$ ist $ a=4 $. Der Funktionsgraph steigt, da $4>1$.
Eine Asymptote ist eine Gerade, an die sich der Graph einer Funktion immer weiter annähert.
LösungSteigende Funktionsgraphen:
Bei der Funktion $ f(x) = 4^x $ ist $a=4$. Es gilt also $ a > 1 $. Wenn du nacheinander in die Funktion für $ x = 1; 2; 3 ... $ einsetzt, Wertepaare bildest und diese in das Koordinatensystem einzeichnest, wird deutlich, dass der Graph steigt.
Allgemein gilt:
Ist die Basis größer $1$, so steigt der Funktionsgraph. Je größer die Basis ist, desto steiler verläuft der Funktionsgraph.
Zum Beispiel gehört der stärker steigende rote Graph in der Darstellung zu $3^x$, der weniger stark steigende gelbe Graph zu $2^x$. Dabei gilt: $3 \gt 2$.Fallende Funktionsgraphen:
Bei der Funktion $ f(x) = (\frac{1}{4})^x $ ist $a=\frac{1}{4} = 0{,}25$. Es gilt also $ a < 1 $. Wenn du hier nacheinander in die Funktion für $ x = 1; 2; 3 ... $ einsetzt, Wertepaare bildest und diese in das Koordinatensystem einzeichnest, wird deutlich, dass der Graph fällt.
Allgemein gilt:
Ist die Basis kleiner $1$, so fällt der Funktionsgraph. Je kleiner die Basis ist, desto steiler verläuft der Funktionsgraph.
Zum Beispiel gehört der stärker fallende rote Graph in der Darstellung zu $\left(\frac{1}{3}\right)^x$, der weniger stark fallende gelbe Graph zu $\left(\frac{1}{2}\right)^x$. Dabei gilt: $\frac{1}{3} \lt \frac{1}{2}$.In beiden Fällen nähert sich der Graph der $x$-Achse immer weiter an, ohne sie zu schneiden. Die $x$-Achse ist demnach stets Asymptote des Graphen.
Das asymptotische Verhalten zweigt sich für $a$ größer $1$ bei $x \to - \infty$, für $a$ kleiner $1$ bei $x \to \infty$. -
Entscheide, welche Aussagen über Exponentialfunktionen korrekt sind.
TippsFür jede beliebige Zahl $a$ gilt: $a^0=1$.
LösungExponentialfunktionen der Form $f(x)=a^x$ haben einige Eigenschaften gemeinsam:
Folgende Aussagen sind korrekt:
- Bei einer Basis $a$ kleiner als $1$ ist der zugehörige Graph streng monoton fallend.
- Alle Exponentialfunktionen haben einen gemeinsamen Punkt $(0 \vert 1)$.
- Jede Exponentialfunktion geht durch den Punkt $(1 \vert a)$.
Folgende Aussagen sind nicht korrekt:
- Jede Exponentialfunktion hat genau eine Nullstelle.
- Die Graphen der Exponentialfunktionen ${f{(x)}=a^x}$ und ${f{(x)}=(\frac{1}{a})^x}$ gehen durch Spiegelung an der $x$-Achse auseinander hervor.
So erhältst du beispielsweise den Graphen von $\left(\frac{1}{7}\right)^x$ durch Spiegelung des Graphen von $7^x$ an der $y$-Achse und umgekehrt.- Alle Exponentialfunktionen gehen durch Stauchung oder Streckung aus $1^x$ hervor.
Der Term $1^x$ entspricht der linearen Funktion $y = 1$, da $1^n = 1$. Es handelt sich also nicht um eine Exponentialfunktion. -
Ermittle den zum Funktionsgraphen passenden Funktionsterm.
TippsFür $a>1$ ist der Graph streng monoton steigend, für $a<1$ ist er streng monoton fallend.
Setze $x=1$ in die Funktionsgleichung ein. Du erhältst den $y$-Wert und kannst überprüfen, welcher Graph den Punkt $P(1|y)$ enthält.
LösungWie erkenne ich einen zugehörigen Funktionsgraphen?
Zuerst schaust du dir die Funktion an und überprüfst, ob die Basis größer oder kleiner $1$ ist. Wenn sie größer $1$ ist, ist der Graph streng monoton steigend, wenn sie kleiner $1$ ist, ist er streng monoton fallend. So kannst du die Graphen schon grob zuordnen.
Außerdem wissen wir, dass für $a \gt 1$ der Graph umso steiler verläuft, je größer die Basis $a$ ist. Für $a \lt 1$ gilt umgekehrt, dass der Graph umso stärker fällt, je näher $a$ an $0$ liegt.
Eine genau Zuordnung ist möglich, indem wir die Lage bestimmter Punkte überprüfen. Wenn du den Punkt $(1|y)$ für steigende bzw. $(-1|y)$ für fallende Graphen ermittelt hast, kannst du den Graphen der Funktion direkt zuordnen.
Bei ${f{(x)}=4^x}$ setzt du den $x$ Wert $1$ ein und erhältst für $y$ den Wert $4$, also $P(1|4)$.
Bei ${f{(x)}=1,5^x}$ setzt du den $x$ Wert $1$ ein und erhältst für $y$ den Wert $1,5$, also $P(1|1,5)$.
Bei ${f{(x)}=(\frac{1}{4})^x}$ setzt du den $x$ Wert $-1$ ein und erhältst für $y$ den Wert $4$, also $P(-1|4)$.
Bei ${f{(x)}=(\frac{1}{6})^x}$ setzt du den $x$ Wert $-1$ ein und erhältst für $y$ den Wert $6$, also $P(-1|6)$.
Du kannst auch den entsprechenden Punkt auf dem Funktionsgraphen ablesen und so den Funktionsterm zuordnen.
-
Berechne die Funktionswerte.
TippsSetze ${x=1}$ in ${f{(x)}=3^x}$ ein und berechne das Ergebnis.
Die Rechnung für $x=3$ wäre hier:
$f(3) = 3^3=3 \cdot 3 \cdot 3=27$.
LösungUm die Funktionswerte von $f(x) = 3^x$ zu bestimmen, werden nacheinander die $x$-Werte eingesetzt und berechnet.
- $f(1) = 3^1=3$
- $f(2) = 3^2=3 \cdot 3=9$
- $f(3) = 3^3=3{\cdot}3{\cdot}3=27$
- $f{(4)} = 3^4=3{\cdot}3{\cdot}3{\cdot}3=81$
- $f(1) = 3$
- $f(2) = 9 = 3 \cdot 3 = f(1) \cdot 3$
- $f(3) = 27 = 9 \cdot 3 = f(2) \cdot 3$
- $f(4) = 81 = 27 \cdot 3 = f(3) \cdot 3$
- $\dots$
-
Prüfe, um welche Art von Funktion es sich handelt.
TippsEine lineare Funktion hat allgemein die Form:
$m \cdot x + b$
Beispiele für Potenzfunktionen:
- $x^2$
- $x^9$
Potenzgesetzte:
LösungErkennen von Funktionstypen:
- Eine Exponentialfunktion erkennst du daran, dass die Variable $x$ im Exponenten auftaucht. Die Basis muss eine von eins verschiedene positive reelle Zahl sein.
- Eine lineare Funktion erkennst du daran, dass die Variable $x$ ohne Exponent auftaucht. Der Funktionsgraph ist eine Gerade.
- Eine Potenzfunktion erkennst du daran, dass die Variable $x$ mit einem Exponenten auftaucht.
Wir betrachten die gegebenen Terme und formen sie, wenn nötig, mithilfe der Potenzgesetze um.
Term 1: $\frac{1}{5^x} = \frac{1^x}{5^x} = \left(\frac{1}{5}\right)^x \Rightarrow$ Es ist eine Exponentialfunktion mit Basis $a= \frac{1}{5}$.
Term 2: $x^3$ ist eine Potenzfunktion mit Exponent $n = 3$.
Term 3: $x^7 \cdot x^{-5} = x^{7-5} = x^2 \Rightarrow$ Es ist eine Potenzfunktion mit Exponent $n = 2$.
Term 4: $3x - 1$ ist eine lineare Funktion mit $m = 3$ und $b = -1$.
Term 5: $7x$ ist eine lineare Funktion mit $m = 7$ und $b = 0$.
Term 6: $7^x$ ist eine Exponentialfunktion mit $a = 7$.
Term 7: $4^{\frac{x}{2}} = 4^{\frac{1}{2} \cdot x} = \left(4^{\frac{1}{2}}\right)^x = \sqrt{4}^x = 2^x \Rightarrow$ Es ist eine Exponentialfunktion mit $a = 2$.
9.908
sofaheld-Level
6.600
vorgefertigte
Vokabeln
8.312
Lernvideos
38.646
Übungen
33.706
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Klassenstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung




 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?