Betragsfunktionen graphisch darstellen


in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
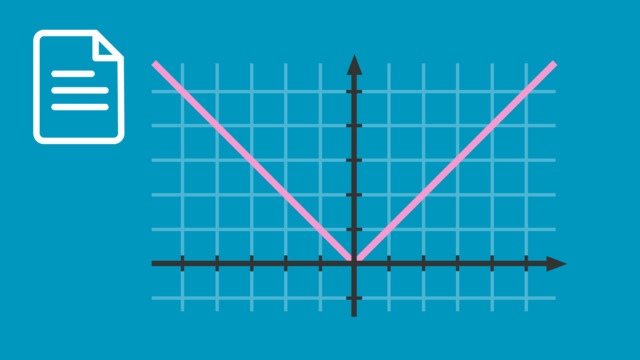
Grundlagen zum Thema Betragsfunktionen graphisch darstellen
Nach dem Schauen dieses Videos wirst du in der Lage sein, Betragsfunktionen graphisch darzustellen.
Zunächst lernst du, was die Eigenschaften von Beträgen und Betragsfunktionen sind. Anschließend lernst du, wie du den Graphen einer Betragsfunktion in einem Koordinatensystem darstellen und dessen Eigenschaften bezüglich seiner Spiegelachse und seines tiefsten Punktes bestimmen kannst. Abschließend lernst du, wie du mittels verschiedener Parameter den Graphen einer Betragsfunktion im Koordinatensystem verschieben sowie dessen Steigung ändern kannst.
Lerne etwas über die Eigenschaften von Betragsfunktionen und deren Graphen, indem du der Billardexpertin Milena zuschaust.
Das Video beinhaltet Schlüsselbegriffe, Bezeichnungen und Fachbegriffe wie die Betragsfunktion, den Graphen einer Betragsfunktion, den Betrag, die Eigenschaften von Betragsfunktionen und deren Graphen.
Bevor du dieses Video schaust, solltest du bereits wissen, was eine lineare Funktion ist.
Nach diesem Video wirst du darauf vorbereitet sein, nichtlineare Funktionen zu lernen.
Transkript Betragsfunktionen graphisch darstellen
Milena ist ein echtes Billardass. Sie möchten ihrem Sohn Jonas alles über das Spiel beibringen. Schauen wir mal, wie die graphische Darstellung von Betragsfunktionen dabei helfen kann, die Kugeln in den Taschen zu versenken. Wiederholen wir zunächst ein paar Grundlagen. Wir wissen schon, dass der Betrag einer Zahl ihr Abstand zur 0 entspricht. Und auch, dass eine positive Zahl und ihre negative Gegenzahl den gleichen Betrag haben. Beispielsweise ist er Betrag von -1 und +1 der Gleiche, nämlich 1. Diese Zahlengerade zeigt die Lösungsmenge für Betrag von x ist gleich 1. x ist gleich +1 und -1. Wir wissen auch, wie man lineare Gleichungen zeichnet. Das ist der Graph von y = 3x + 2. Zeichnen wir aber eine Betragsfunktion, bekommen wir etwas völlig anderes. Fangen wir mit der einfachsten Betragsfunktion an: y = |x|. Wenn du für x 1, 2, 3 und so weiter einsetzt, bekommst du einen Graphen, der zunächst einmal an den einer linearen Gleichung erinnert. Aber Moment mal, das ist ja nur der eine Teil des Graphen! Sieh dir an, was bei x = -1, -2, -3 und so weiter passiert. Der Graph hat jetzt eine V-Form. Und das gilt für alle Graphen von Betragsfunktionen. Daran kann man sie ganz leicht erkennen. Der Scheitelpunkt ist der tiefste beziehungsweise höchste Punkt des Graphen einer Betragsfunktion. Die Spiegelachse verläuft vertikal durch diesen Punkt. Alle Änderungen der Ausgangsfunktion ändern den Graphen. Wir addieren 1, die Funktion lautet nun y = |x+1|. Der Graph hat sich um eine Einheit nach links verschoben, hat sich ansonsten aber nicht verändert. Was passiert deiner Meinung nach, wenn man 2 zu x addiert? Im Vergleich zum ursprünglichen Graphen hat sich der Graph um 2 Einheiten nach links verschoben. Jetzt subtrahieren wir 2 von x dieses Mal verschiebt sich der Graph um 2 Einheiten nach rechts. Erkennst du das Muster? Die Gegenzahl dieser Konstanten, also die Zahl mit getauschtem Vorzeichen, ist die x-Koordinate des Scheitelpunkts. des tiefsten Punkts. Spielen wir noch ein bisschen herum. Dieses Mal addieren wir 1 außerhalb der Betragsstriche. Wie verändert das den ursprünglichen Graphen? Der Scheitelpunkt tiefste Punkt verschiebt sich nach oben, und mit ihm der ganze Graph. Addierst du 2, verschiebst sich der Graph um 2 Einheiten nach oben. Und wenn du 2 subtrahierst? Dann verschiebt sich der Graph um 2 Einheiten nach unten. Und eine letzte Änderung. Was passiert, wenn du den Betrag mal 2 nimmst? Der Scheitelpunkt tiefste Punkt bleibt gleich, aber die Steigung ändert sich. Bisher war sie 1, nun ist sie 2. Und wenn du den Betrag mal 3 nimmst? Ach was, je größer der Faktor, desto enger wird der Graph und desto steiler wird die Steigung. Und wenn wir mit 1/2 multiplizieren? Jetzt öffnet sich der Graph und die Steigung wird flacher. Hast du eine Idee, was passiert, wenn wir die ursprüngliche Funktion mal -2 nehmen? Sieh dir das an. Der Graph klappt nach unten! Nun weißt du, wie man Betragsfunktionen zeichnet. Also zurück zum Billardtisch. Schau dir die Bahn der Kugel an. Ein vertrautes Bild, nicht wahr? Eine V-Form, ganz so wie beim Graphen einer Betragsfunktion. Stellen wir eine Gleichung für die Bahn auf. Wir beginnen mit der Funktion y = |x|. Dann addieren oder subtrahieren wir innerhalb der Betragszeichen. Oder wir addieren oder subtrahieren außerhalb der Betragszeichen. Oder wir multiplizieren den Betrag mit einem Faktor. Die Bahn der Kugel hat ihren Scheitelpunkt tiefsten Punkt bei (6|0). Der Scheitelpunkt tiefste Punkt ist also 6 Einheiten rechts vom Ursprung, also subtrahieren wir 6 innerhalb der Betragszeichen. Da die y-Koordinate des Scheitelpunktes tiefsten Punktes 0 ist, müssen wir außerhalb der Betragszeichen nichts addieren oder subtrahieren. Aber das passt noch nicht ganz. Der Graph der gesuchten Funktion ist enger, also müssen wir den Betragsterm mit einem positiven Faktor multiplizieren. Wie ist die Steigung? Delta y ist 2, Delta x ist 1. Die Steigung entspricht Delta y durch Delta x, also 2. Keine Ahnung, ob Jonas seiner Mutter zugehört hat die Billardkreide hat ihn wohl mehr fasziniert.
Betragsfunktionen graphisch darstellen Übung
-
Gib die Eigenschaften der Betragsfunktion $f(x)$ an.
TippsDer Betrag einer Zahl entspricht ihrem Abstand zur $0$.
Eine positive Zahl und ihre negative Gegenzahl haben den gleichen Betrag. Es gilt also:
$|1|=|-1|=1$
Eine Wertetabelle für die Betragsfunktion $f(x)=|x|$ ist wie folgt gegeben:
$ \\ \begin{array}{l|rrrrrrr} x & -3 & -2 & -1 & 0 & 1 & 2 & 3 \\ \hline f(x) & 3 & 2 & 1 & 0 & 1 & 2 & 3 \end{array} $
LösungIm Folgenden schauen wir uns die Eigenschaften der Betragsfunktion $f(x)=|x|$ an:
Der Betrag einer Zahl entspricht ihrem Abstand zur $0$. Demnach haben eine positive Zahl und ihre negative Gegenzahl den gleichen Betrag. Es gilt also:
$|1|=1=|-1|$
Für unsere Betragsfunktion $f(x)$ ergibt sich somit die folgende Wertetabelle:
$ \begin{array}{l|r|r|r|r|r|r|r|r|r|r|r} x & -5 & -4 & -3 & -2 & -1 & 0 & 1 & 2 & 3 & 4 & 5\\ \hline f(x) & 5 & 4 & 3 & 2 & 1 & 0 & 1 & 2 & 3 & 4 & 5 \end{array} $
Der zugehörige Funktionsgraph ist hier abgebildet. Dieser hat eine V-Form, was für alle Graphen von Betragsfunktionen gilt. Daran kann man sie ganz leicht erkennen.
Die Spitze des Graphen der Betragsfunktion ist der tiefste Punkt des Graphen, nämlich $S(0\vert 0)$. Die Spiegelachse verläuft vertikal durch diesen Punkt.
-
Bestimme die Funktionsgleichungen der gegebenen Graphen.
TippsDurch Variation des Parameters $b$ einer Betragsfunktion der Form $f(x)=b+|x|$ wird der zugehörige Graph gegenüber dem Graphen zu $|x|$ entlang der $y$-Achse um $b$ Einheiten verschoben.
Durch Variation des Parameters $a$ einer Betragsfunktion der Form $f(x)=|x-a|$ wird der zugehörige Graph gegenüber dem Graphen zu $|x|$ entlang der $x$-Achse um $a$ Einheiten verschoben.
Durch Variation des Parameters $c$ einer Betragsfunktion der Form $f(x)=c\cdot |x|$ ändert der zugehörige Graph seine Steigung und Richtung der Öffnung. Es gilt:
1. Fall
$|c|>1$
Der Graph besitzt gegenüber dem Graphen zu $|x|$ eine größere Steigung und wird somit enger.
2. Fall
$0<|c|<1$
Der Graph besitzt gegenüber dem Graphen zu $|x|$ eine kleinere Steigung und wird somit breiter.
3 Fall
$c<0$
Ist der Faktor negativ, so klappt sich der Graph mit der entsprechenden Steigung nach unten.
LösungBevor wir die Funktionen der gegebenen Graphen bestimmen, wiederholen wir zunächst den Einfluss der einzelnen Parameter in der allgemeinen Betragsfunktion $f(x)=c\cdot |x-a|+b$. Diese Funktion ist gegenüber der Betragsfunktion $g(x)=|x|$:
- um $a$ Einheiten entlang der $x$-Achse verschoben und
- um $b$ Einheiten entlang der $y$-Achse verschoben.
Durch Variation des Parameters $c$ ändert der zugehörige Graph seine Steigung und Richtung der Öffnung. Es gilt:
- $|c|>1$: Der Graph hat gegenüber $g(x)=|x|$ eine größere Steigung und ist somit enger.
- $0<|c|<1$: Der Graph hat gegenüber $g(x)=|x|$ eine kleinere Steigung und ist somit breiter.
- $c>0$: Ist der Faktor positiv, so ist der Graph nach oben geöffnet.
- $c<0$: Ist der Faktor negativ, so ist der Graph nach unten geöffnet.
Nun können wir die Funktionsgleichungen der gegebenen Graphen bestimmen.
1. Graph
Dieser Graph ist gegenüber der Betragsfunktion $g(x)=|x|$ um $2$ Einheiten entlang der $x$-Achse nach rechts verschoben. Wir setzen in die Betragsfunktion $a=2$. Die Parameter $b$ und $c$ brauchen wir nicht zu berücksichtigen, da weder eine Verschiebung entlang der $y$-Achse noch eine Streckung, Stauchung oder Spiegelung an der $x$-Achse vorliegt. Wir erhalten somit:
$f(x)=|x-2|$
2. Graph
Dieser Graph ist gegenüber der Betragsfunktion $g(x)=|x|$ entlang der $y$-Achse gestreckt. Wir haben also eine größere Steigung, welche wir mithilfe eines Steigungsdreiecks bestimmen können:
$c=\frac{\Delta y}{\Delta x}=\frac 42=2$
Die Parameter $a$ und $b$ brauchen wir nicht zu berücksichtigen, da weder entlang der $x$-Achse noch entlang der $y$-Achse verschoben wurde. Wir erhalten somit:
$f(x)=2\cdot |x|$
3. Graph
Dieser Graph ist gegenüber der Betragsfunktion $g(x)=|x|$ um $2$ Einheiten entlang der $y$-Achse nach oben verschoben. Wir setzen in die Betragsfunktion $b=2$. Die Parameter $a$ und $c$ brauchen wir nicht zu berücksichtigen, da weder eine Verschiebung entlang der $x$-Achse noch eine Streckung, Stauchung oder Spiegelung an der $x$-Achse vorliegt. Wir erhalten somit:
$f(x)=2+|x|$
4. Graph
Dieser Graph ist gegenüber der Betragsfunktion $g(x)=|x|$ um $2$ Einheiten entlang der $x$-Achse nach links verschoben. Wir setzen in die Betragsfunktion $a=-2$. Die Parameter $b$ und $c$ brauchen wir nicht zu berücksichtigen, da weder eine Verschiebung entlang der $y$-Achse noch eine Streckung, Stauchung oder Spiegelung an der $x$-Achse vorliegt. Wir erhalten somit:
$f(x)=|x+2|$
-
Ermittle die Funktionsgleichung $f(x)$ des gegebenen Funktionsgraphen.
TippsDurch Variation des Parameters $b$ einer Betragsfunktion der Form $f(x)=|x-a|+b$ wird der zugehörige Graph gegenüber dem Graphen zu $|x-a|$ entlang der $y$-Achse um $b$ Einheiten verschoben.
Durch Variation des Parameters $a$ einer Betragsfunktion der Form $f(x)=|x-a|+b$ wird der zugehörige Graph gegenüber dem Graphen zu $|x|+b$ entlang der $x$-Achse um $a$ Einheiten verschoben.
Die Funktionsgleichung des hier abgebildeten Graphen lautet:
$f(x)=|x-1|$
LösungDie Parameter $a$ und $b$ einer Betragsfunktion der Form $f(x)=|x-a|+b$ verschieben den Graphen zu $|x|$:
- um $a$ Einheiten entlang der $x$-Achse und
- um $b$ Einheiten entlang der $y$-Achse.
Demnach können wir den drei Graphen folgende Funktionsgleichungen zuordnen:
Graph zu $f(x)$
Der Graph zu $f(x)$ ist gegenüber dem Graphen zu $|x|$ um eine Einheit entlang der $x$-Achse nach rechts und um drei Einheiten entlang der $y$-Achse nach oben verschoben. Mit $a=1$ und $b=3$ erhalten wir:
$f(x)=|x-1|+3$
Graph zu $g(x)$
Der Graph zu $g(x)$ ist gegenüber dem Graphen zu $|x|$ um drei Einheiten entlang der $x$-Achse nach rechts und um zwei Einheiten entlang der $y$-Achse nach unten verschoben. Mit $a=3$ und $b=-2$ erhalten wir:
$f(x)=|x-3|-2$
Graph zu $h(x)$
Der Graph zu $h(x)$ ist gegenüber dem Graphen zu $|x|$ um eine Einheit entlang der $x$-Achse nach links und um zwei Einheiten entlang der $y$-Achse nach unten verschoben. Mit $a=-1$ und $b=-2$ erhalten wir:
$f(x)=|x-(-1)|-2=|x+1|-2$
-
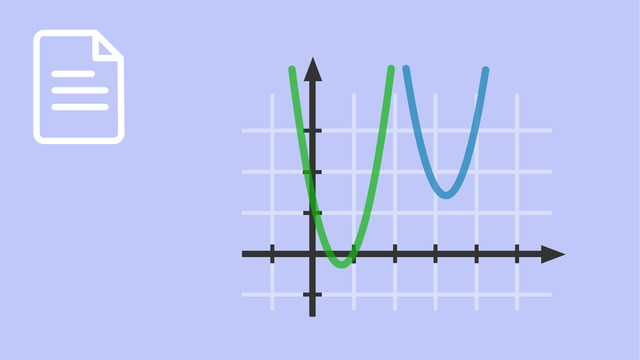
Erschließe aus den gegebenen Graphen den Parameter $c$ der Funktionsgleichungen.
TippsBetrachte nur den Teil des jeweiligen Graphen, welcher im ersten oder vierten Quadranten liegt. Dann entspricht der Wert für den Parameter $c$ der jeweiligen Geradensteigung:
$c=\frac{\Delta y}{\Delta x}$
Für den Parameter $c$ gibt es folgende Fälle:
1. Fall
$|c|>1$
Der Graph besitzt gegenüber dem Graphen zu $|x|$ eine größere Steigung und wird somit enger.
2. Fall
$0<|c|<1$
Der Graph besitzt gegenüber dem Graphen zu $|x|$ eine kleinere Steigung und wird somit breiter.
3. Fall
$c<0$
Ist der Faktor negativ, so klappt sich der Graph mit der entsprechenden Steigung nach unten.
LösungWenn wir die Steigung des Graphen einer Betragsfunktion der Form $f(x)=c\cdot |x|$ bestimmen möchten, so können wir einfach den Teil des jeweiligen Graphen betrachten, welcher im ersten oder vierten Quadranten liegt. Dann entspricht der Wert für den Parameter $c$ der jeweiligen Geradensteigung:
$c=\frac{\Delta y}{\Delta x}$.
Dabei gelten folgende Zusammenhänge:
- $|c|>1$: Graph hat gegenüber dem Graphen zu $|x|$ eine größere Steigung und ist somit enger.
- $0<|c|<1$: Graph hat gegenüber dem Graphen zu $|x|$ eine kleinere Steigung und ist somit breiter.
- $c<0$: Ist der Faktor negativ, so klappt sich der Graph mit der entsprechenden Steigung nach unten.
Wir haben insgesamt drei Graphen, welche nach oben geöffnet sind, und nur einen, der nach unten geöffnet ist. Somit ist nur einer der vier Werte für $c$ negativ.
Für $c$ erhalten wir folgende Lösungen:
Grüner Graph
$c=\frac{\Delta y}{\Delta x}=\frac 31=3$
Blauer Graph
$c=\frac{\Delta y}{\Delta x}=\frac 21=2$
Roter Graph
$c=\frac{\Delta y}{\Delta x}=\frac 12$
Oranger Graph
$c=\frac{\Delta y}{\Delta x}=\frac {-1}1=-1$
-
Vervollständige die Wertetabelle zu der Funktion $f(x)$.
TippsDer Betrag einer Zahl entspricht ihrem Abstand zur $0$. Demnach haben eine positive Zahl und ihre negative Gegenzahl den gleichen Betrag. Es gilt also:
$|5|=5=|-5|$
Nachdem du den Betrag bestimmt hast, musst du bei der weiteren Berechnung Punkt- vor Strichrechnung berücksichtigen.
Schau dir folgendes Beispiel an:
$ \begin{array}{lll} 5\cdot |1-8|+10 &=& 5\cdot |-7|+10 \\ &=& 5\cdot 7+10 \\ &=& 35+10 \\ &=& 45 \end{array} $
LösungWir möchten für die Funktion $f(x)=3\cdot |x-1|+1$ die fehlenden Funktionswerte der folgenden Wertetabelle bestimmen:
$ \begin{array}{l|r|r|r|r} x & -1 & 0& 1& 2 \\ \hline f(x) &&&& \end{array} $
Hierzu setzen wir je einen $x$-Wert in die Funktionsgleichung ein und berechnen zunächst den Betrag. Anschließend rechnen wir weiter, indem wir Punkt- vor Strichrechnung beachten. Die Berechnung des Funktionswertes für den ersten $x$-Wert lautet wie folgt:
$ \begin{array}{lll} 3\cdot |-1-1|+1 &=& 3\cdot |-2|+1 \\ &=& 3\cdot 2+1 \\ &=& 6+1 \\ &=& 7 \end{array} $
So machst du es für die übrigen drei $x$-Werte. Dadurch ergibt sich folgende Wertetabelle:
$ \begin{array}{l|r|r|r|r} x & -1 & 0& 1& 2 \\ \hline f(x) & 7 & 4 & 1 & 4 \end{array} $
-
Bestimme die gesuchte Funktionsgleichung des gegebenen Graphen.
TippsIst der Parameter $c$ einer Funktion der Form $f(x)=c\cdot |x-a|+b$ negativ, so ist der Graph nach unten geöffnet.
Der hier abgebildete Graph hat die Funktionsgleichung $f(x)=-|x-1|+2$.
LösungWir suchen die Parameter $a$, $b$ und $c$ der Funktionsgleichung $f(x)=c\cdot |x-a|+b$.
Parameter $a$
Dieser Parameter gibt an, um wie viele Einheiten der Graph gegenüber dem Graphen zu $|x|$ entlang der $x$-Achse verschoben ist. Der Graph der Funktion $f(x)$ ist um vier Einheiten nach rechts verschoben. Es ist also $a=4$.
Parameter $b$
Dieser Parameter gibt an, um wie viele Einheiten der Graph gegenüber dem Graphen zu $|x|$ entlang der $y$-Achse verschoben ist. Der Graph der Funktion $f(x)$ ist um zwei Einheiten nach oben verschoben. Es ist also $b=2$.
Parameter $c$
Dieser Parameter gibt die Steigung sowie die Richtung der Öffnung des Graphen an. Hier ist $c$ negativ, denn der Graph ist nach unten geöffnet. Zudem ist der Graph der Funktion $f(x)$ gegenüber dem Graphen zu $|x|$ entlang der $y$-Achse gestreckt, also enger. Wir erhalten für den Parameter $c$ den folgenden Wert:
$c=\frac{\Delta y}{\Delta x}=\frac {-4}2=-2$
Funktionsgleichung
Daraus resultiert die Funktionsgleichung $~f(x)=-2\cdot |x-4|+2$.
9.853
sofaheld-Level
6.600
vorgefertigte
Vokabeln
8.306
Lernvideos
38.657
Übungen
33.694
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Klassenstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung




 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?