Vektorräume

Inhaltsverzeichnis zum Thema

• Was ist ein Vektorraum?
• Operationen in einem Vektorraum
• Regeln in einem Vektorraum
• Beispiele für Vektorräume
• Die Menge der reellen Zahlen $\mathbb{R}$
• Die Ebene $\mathbb{R^2}$
• Der Raum $\mathbb{R^3}$
• Eine Basis eines Vektorraumes

Was ist ein Vektorraum?

Ein Vektorraum wird auch als linearer Raum bezeichnet. Hier kannst du einen zweidimensionalen Vektorraum erkennen:

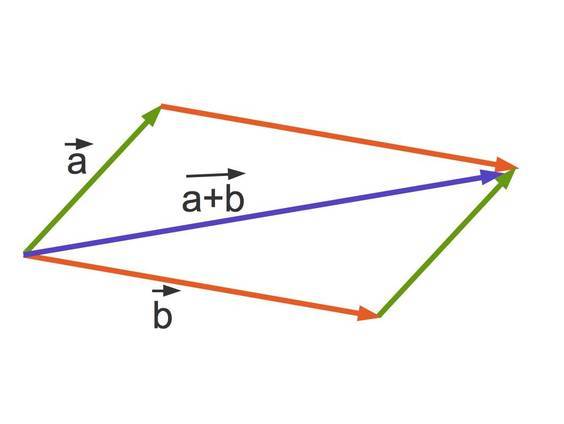
Die Elemente eines Vektorraums werden Vektoren genannt, mit denen dank der folgenden Operationen gerechnet werden kann.

Operationen in einem Vektorraum

Es seien $a$ und $b$ Vektoren und $u \in \mathbb{R}$ ein Skalar. Vektoren $a$ und $b$ können

• addiert werden: $a+b$,
• mit einem Skalar $u$ multipliziert werden: $u\cdot a$. Diese Multiplikation wird als skalare Multiplikation bezeichnet.

Die jeweiligen Ergebnisse $a+b$ und $u\cdot a$ sind wieder Vektoren.

Durch die Multiplikation eines Vektors mit $-1$ wird die Differenz von Vektoren ermöglicht:

$a-b=a+(-1)\cdot b$.

Ein Vektorraum liegt vor, wenn die folgenden Regeln erfüllt sind. Diese Regeln werden auch Axiome genannt.

Regeln in einem Vektorraum

Es seien $a$, $b$ und $c$ Vektoren des Vektorraums und $u$ sowie $v$ Skalare, dann gelten in einem Vektorraum die folgenden Regeln.

Für die Addition zweier Vektoren muss gelten:

1. das Assoziativgesetz: $(a+b)+c=a+(b+c)$.
2. das Kommutativgesetz: $a+b=b+a$.
3. die Existenz des neutralen Elementes: $a+0=a$.
4. die Existenz des inversen Elementes: $a+(-a)=0$.

Für die skalare Multiplikation eines Vektors mit einem Skalar muss gelten:

1. das Distributivgesetz 1: $(u+v)\cdot a=u\cdot a+v\cdot a$.
2. das Distributivgesetz 2: $u\cdot(a+b)=u\cdot a+u\cdot b$.
3. die Existenz des neutralen Elementes: $1\cdot a=a$. Dabei ist $1$ eine reelle Zahl.
4. das Assoziativgesetz: $(u\cdot v)\cdot a=u\cdot (v\cdot a)$.

Dabei solltest du dir klar machen, dass für die Multiplikation von Skalaren als auch für die skalare Multiplikation das gleiche Operationszeichen verwendet wird. In dem jeweiligen Kontext sollte aber klar sein, welche Multiplikation gemeint ist.

Schauen wir uns ein paar Beispiele an.

Beispiele für Vektorräume

Die Menge der reellen Zahlen $\mathbb{R}$

Die Menge der reellen Zahlen $\mathbb{R}$ ist ein Zahlenbereich. $\mathbb{R}$ ist auch ein Vektorraum, da die obigen Axiome erfüllt sind:

• Das Kommutativgesetz der Addition (Multiplikation) besagt, dass die Reihenfolge bei der Addition (Multiplikation) vertauschbar ist.
• Das Assoziativgesetz der Addition (Multiplikation) beschreibt, dass es egal ist, in welcher Reihenfolge mehr als zwei Summanden (Faktoren) addiert (multipliziert) werden.
• Das neutrale Element der Addition (Multiplikation) ist die reelle Zahl $0$ ($1$).
• Das inverse Element der Addition (Multiplikation) erhältst du durch Vertauschen des Vorzeichens der Zahl (Bilden des Kehrwertes von reellen Zahlen ohne $0$).
• Das Distributivgesetz dient dazu, Klammern auszumultiplizieren, zum Beispiel $2(3+x)=6+2x$.

Die Ebene $\mathbb{R^2}$

Die Elemente in diesem Vektorraum sind zweidimensionale Vektoren.

$\vec v=\begin{pmatrix} v_1 \\ v_2 \end{pmatrix}$

Die Axiome gelten auch hier. Allerdings sind Addition und Multiplikation etwas anders definiert.

Zwei Vektoren werden addiert, indem die einzelnen Koordinaten addiert werden. Dies ist die Vektoraddition:

$\vec v+\vec w=\begin{pmatrix} v_1 \\ v_2 \end{pmatrix}+\begin{pmatrix} w_1 \\ w_2 \end{pmatrix}=\begin{pmatrix} v_1+w_1 \\ v_2 +w_2 \end{pmatrix}$

Bei der skalaren Multiplikation wird jede Koordinate des Vektors mit dem Skalar multipliziert:

$k\cdot \vec v=k\cdot \begin{pmatrix} v_1 \\ v_2 \end{pmatrix}=\begin{pmatrix} k\cdot v_1\\ k\cdot v_2 \end{pmatrix}$

Die Überprüfung des Kommutativgesetzes, der Assoziativgesetze sowie der Distributivgesetze kann koordinatenweise durchgeführt werden. Jede Koordinate eines Vektors ist eine reelle Zahl.

Das neutrale Element der Addition ist der Nullvektor

$\vec 0=\begin{pmatrix} 0 \\ 0 \end{pmatrix}$

Das inverse Element der Addition ist der Gegenvektor. Hier wird in jeder Koordinate des Vektors das Vorzeichen vertauscht.

$-\vec v=-\begin{pmatrix} v_1 \\ v_2 \end{pmatrix}=\begin{pmatrix} -v_1 \\ -v_2 \end{pmatrix}$

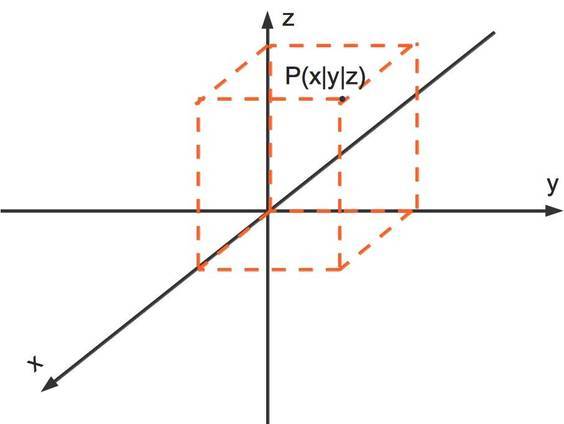
Der Raum $\mathbb{R^3}$

Die Elemente in diesem Raum sind dreidimensionale Vektoren. Im Gegensatz zu den Elementen des $\mathbb{R^2}$ haben sie 3 Koordinaten. Der Nachweis der Vektorraumeigenschaften erfolgt vollkommen analog.

Eine Basis eines Vektorraumes

Die Basis eines Vektorraumes ist eine Menge an Vektoren. Diese Vektoren werden als Basisvektoren bezeichnet. Mithilfe der Basisvektoren kann jeder beliebige Vektor des Vektorraumes durch Addition und skalare Multiplikation eindeutig dargestellt werden.

Die Basis ist dabei minimal. Es darf also kein Vektor aus der Basis entfernt werden, da sich ansonsten nicht mehr alle Vektoren darstellen ließen. Das bedeutet, dass die Anzahl der Basisvektoren in jeder beliebigen Basis immer gleich groß ist.

Diese Anzahl der Vektoren in einer Basis bestimmt die Dimension des Vektorraumes.

• Die Menge der reellen Zahlen $\mathbb{R}$ hat die Dimension $1$. Eine reelle Zahl kann somit als eindimensionaler Vektor verstanden werden.
• Die Ebene $\mathbb{R^2}$ hat die Dimension $2$. Eine Basis ist durch diese Vektoren gegeben:

$\quad~~~\begin{pmatrix} 1 \\ 0 \end{pmatrix}, \begin{pmatrix} 0 \\ 1 \end{pmatrix}$

• Der Raum $\mathbb{R^3}$ hat die Dimension $3$. Die Basis lässt sich analog zu $\mathbb{R^2}$ erweitern.

Wie genau eine Basis genutzt werden kann, um einen Vektorraum aufzuspannen, muss im Kontext von Linearkombinationen untersucht werden.