Ganzrationale Funktionen – Kurvendiskussion

Inhaltsverzeichnis zum Thema

• Was ist eine ganzrationale Funktion?
• Der Definitionsbereich und der Wertebereich
• Symmetrie
• Die Nullstellen
• Die Extrema
• Die notwendige Bedingung
• Die hinreichende Bedingung
• Bestimmung der Extrema
• Monotonie und Verhalten der Funktion im Unendlichen
• Monotonie
• Das Verhalten der Funktion im Unendlichen
• Die Wendepunkte
• Die notwendige Bedingung
• Die hinreichende Bedingung
• Bestimmung der Wendepunkte
• Der Graph der Funktion

Was ist eine ganzrationale Funktion?

Eine ganzrationale Funktion oder auch Polynom sieht wie folgt aus:

$f(x)=a_n\cdot x^n+a_{n-1}\cdot x^{n-1}+\dots +a_2x^2+a_1x+a_0$.

Es muss $a_n\neq 0$ gelten.

• Der Grad dieser Funktion ist der höchste Exponent $n$.
• Die Faktoren $a_n$, ..., $a_2$, $a_1$ sowie $a_0$ vor den Potenzen sind die Koeffizienten des Polynoms.

Hier siehst du einige Beispiel für Polynome:

• $f(x)=4$ ist eine konstante Funktion, ein Polynom vom Grad $0$.
• $f(x)=2x-3$ ist eine lineare Funktion, ein Polynom vom Grad $1$.
• $f(x)=0,5x^2-3x$ ist eine quadratische Funktion, ein Polynom vom Grad $2$.
• $f(x)=2x^3-3x+1$ ist eine kubische Funktion, ein Polynom vom Grad $3$.
• $f(x)=0,2x^4-2x^2+3,2$ ist eine biquadratische Funktion, ein Polynom vom Grad $4$.

Im Folgenden wirst du eine Kurvendiskussion am Beispiel der biquadratischen Funktion $f(x)=0,2x^4-2x^2+3,2$ sehen.

Der Definitionsbereich und der Wertebereich

• Der Definitionsbereich oder auch die Definitionsmenge einer ganzrationalen Funktion ist $\mathbb{D}_f=\mathbb{R}$, also die Menge aller reellen Zahlen. Das bedeutet, es gibt keine Einschränkungen (Definitionslücken) beim Definitionsbereich.
• Der Wertebereich $\mathbb{W}_f$ einer Funktion ist die Menge aller Werte, welche die Funktion annimmt. Hierfür kannst du dir die Extrema sowie die Grenzwerte der Funktion anschauen.

Symmetrie

Bei ganzrationalen Funktionen kannst die Symmetrie mit Hilfe der Exponenten untersuchen:

• Wenn alle Exponenten gerade sind, ist die Funktion achsensymmetrisch zur y-Achse oder auch gerade symmetrisch.
• Sind alle Exponenten ungerade, ist die Funktion punktsymmetrisch zum Koordinatenursprung oder auch ungerade symmetrisch.
• Andernfalls liegt keine der beiden obigen Symmetrien vor.

$f(x)=0,2x^4-2x^2+3,2$ hat nur gerade Exponenten ($4$, $2$ und $0$). Diese Funktion ist achsensymmetrisch zur y-Achse.

Die Nullstellen

Die Nullstellen einer Funktion $f(x)$ sind alle Werte für das Argument $x$ der Funktion, für die $f(x)=0$ gilt.

Du musst also die Gleichung

$0,2x^4-2x^2+3,2=0$

lösen. Eine solche biquadratische Gleichungen löst du, indem du $z=x^2$ substituierst. Dies führt zu der quadratischen Gleichung in $z=x^2$

$0,2z^2-2z+3,2=0$.

Daher kommt der Name der Funktion wie auch der Gleichung. Diese Gleichung löst du nun mit der pq-Formel:

$\begin{array}{crclll} &0,2z^2-2z+3,2&=&0&|&\cdot 5\\ \Leftrightarrow&z^2-10z+16&=&0\\\\ &z_{1,2}&=&5\pm\sqrt{5^2-16}\\ &&=&5\pm\sqrt9\\ &z_1&=&5+3=8\\ &z_2&=&5-3=2 \end{array}$

Dies sind die Lösungen für $z$. Nun musst du resubstituieren, also $x^2=z$.

• Für $z_1=8$ führt dies durch das Ziehen der Wurzel zu den beiden Lösungen $x_{11}=-\sqrt8$ sowie $x_{12}=\sqrt8$.
• Für $z_2=2$ führt dies durch das Ziehen der Wurzel zu den weiteren Lösungen $x_{21}=-\sqrt2$ sowie $x_{22}=\sqrt2$.

Du kannst diese Nullstellen (grün) bereits in ein Koordinatensystem einzeichnen:

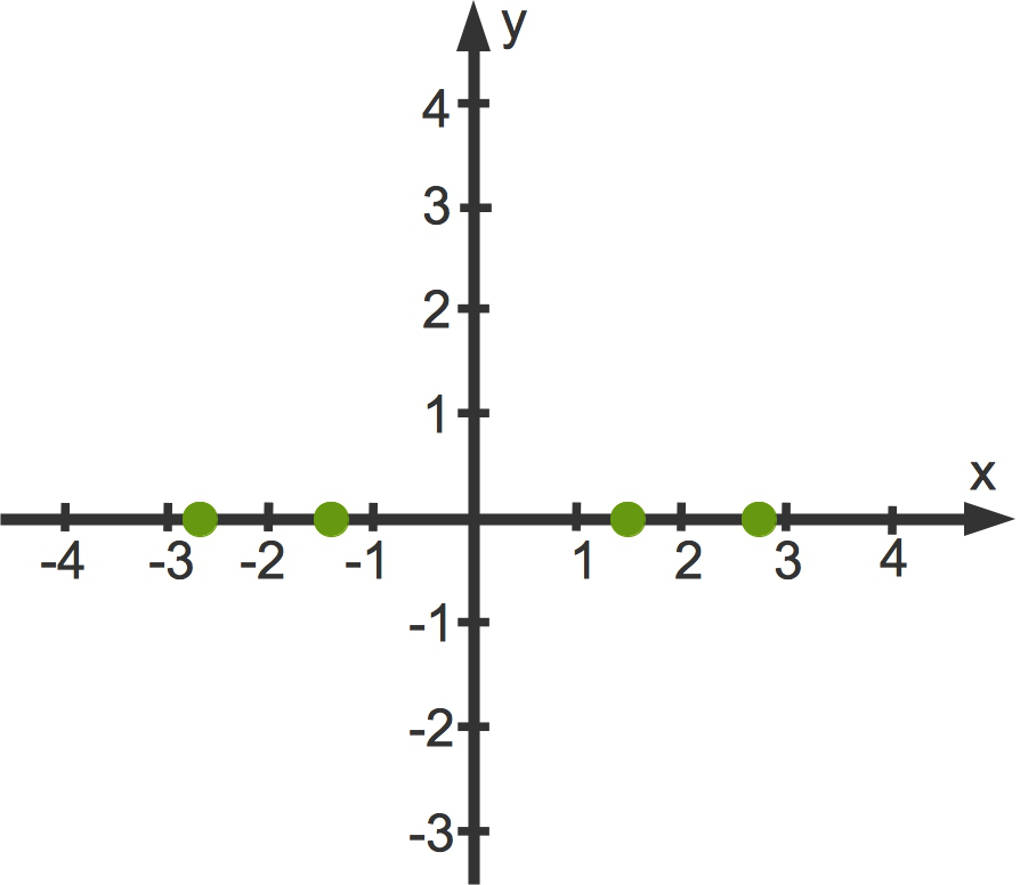
Die Extrema

Um eine Funktion auf Extrema zu untersuchen, prüfst du eine notwendige sowie eine hinreichende Bedingung mit der ersten und zweiten Ableitung. Diese sind

$f'(x)=0,8x^3-4x$

sowie

$f''(x)=2,4x^2-4$.

Die notwendige Bedingung

Es muss gelten $f'(x)=0$. Anschaulich bedeutet dies, dass an den entsprechenden Stellen eine waagerechte Tangente vorliegt: $0,8x^3-4x=0$.

• Klammere $x$ aus: $x\cdot (0,8x^2-4)=0$.
• Ein Produkt wird $0$, wenn einer der Faktoren $0$ wird, also ist entweder $x_{E_1}=0$ oder $0,8x^2-4=0$.
• Addiere $4$ zu der Gleichung zu $0,8x^2=4$. Division durch $0,8$ führt zu $x^2=5$. Nun kannst du die Wurzel ziehen und erhältst $x_{E_2}=-\sqrt 5$ sowie $x_{E_3}=\sqrt 5$.

Es gibt Punkte, in denen eine waagerechte Tangente vorliegt, die trotzdem keine Extrema sind. Solche Punkte werden Sattelpunkte genannt.

Die hinreichende Bedingung

Zusätzlich zu der notwendigen Bedingung muss $f''(x_E)$ für die gefundenen Extremstellen gelten. Wenn die zweite Ableitung ungleich $0$ ist, ist sie

• entweder kleiner als $0$, dann liegt ein (lokaler) Hochpunkt vor

• oder größer als $0$, dann liegt ein (lokaler) Tiefpunkt vor.

• $x_{E_1}=0$: $f''(0)=-4<0$. Dies bedeutet, dass hier ein (lokaler) Hochpunkt vorliegt.

• $x_{E_2}=-\sqrt 5$: $f''(-\sqrt 5)=2,4(-\sqrt 5)^2-4=8>0$, also liegt hier ein (lokaler) Tiefpunkt vor.
• $x_{E_3}=\sqrt 5$: $f''(\sqrt 5)=2,4(\sqrt 5)^2-4=8>0$, auch hier liegt ein (lokaler) Tiefpunkt vor.

Bestimmung der Extrema

Zuletzt gibst du noch die Extrempunkte an. Hierfür musst du zu jeder Extremstelle den Funktionswert durch Einsetzen in der Funktionsgleichung bestimmen:

• $f(0)=3,2~\rightarrow~HP(0|3,2)$
• $f(-\sqrt5)=0,2(-\sqrt5)^4-2(-\sqrt 5)^2+3,2=-1,8$ $\rightarrow$ $TP(-\sqrt 5|-1,8)$
• $f(\sqrt5)=0,2(\sqrt5)^4-2(\sqrt 5)^2+3,2=-1,8$ $\rightarrow$ $TP(\sqrt 5|-1,8)$

Trage auch die Extrema (rot) in das Koordinatensystem ein:

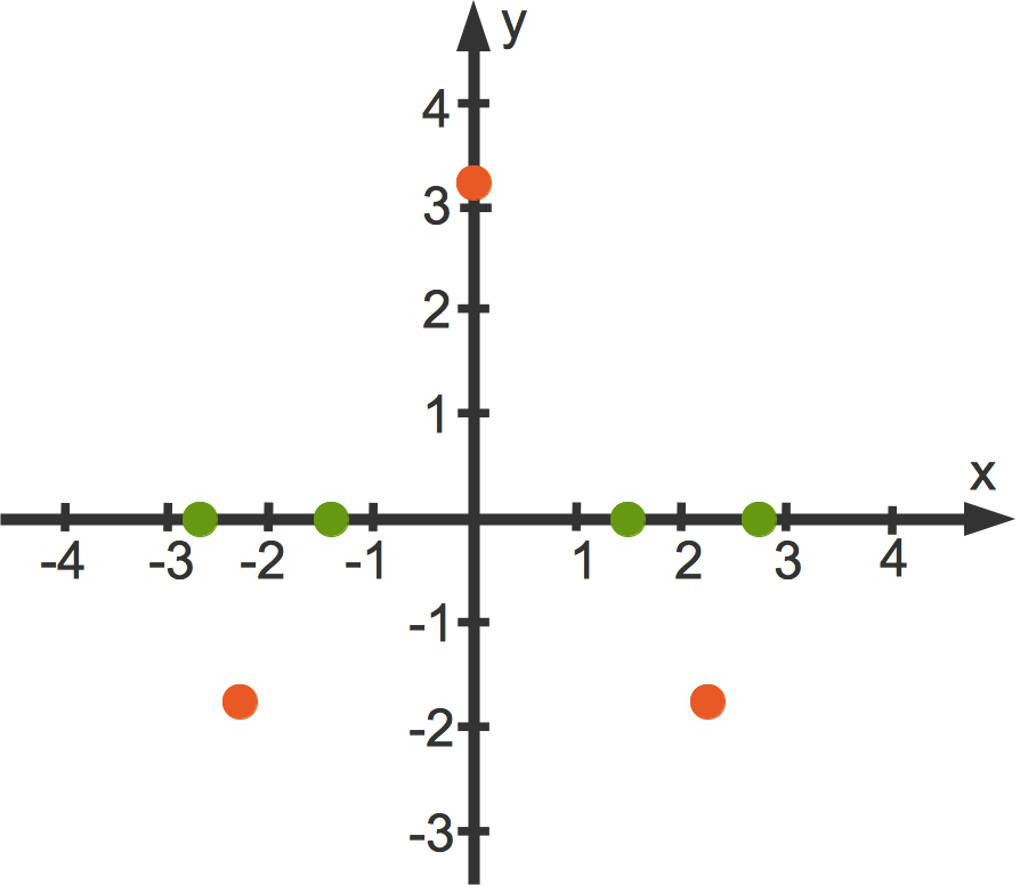
Monotonie und Verhalten der Funktion im Unendlichen

Monotonie

Das Monotonieverhalten der Funktion kannst du nun bestimmen:

• Für $x<-\sqrt5$ ist die Funktion monoton fallend.
• Nun kommt der Tiefpunkt $TP(-\sqrt 5|-1,8)$.
• Für $-\sqrt5 < x < 0$ ist die Funktion monoton steigend.
• Nun kommt der Hochpunkt $HP(0|3,2)$.
• Für $0 < x < \sqrt5$ ist die Funktion monoton fallend.
• Nun kommt der Tiefpunkt $TP(\sqrt 5|-1,8)$.
• Für $x > \sqrt 5$ ist die Funktion monoton steigend.

Das Verhalten der Funktion im Unendlichen

Wie ist das Verhalten ganzrationaler Funktionen im Unendlichen? Da die Funktion symmetrisch zur y-Achse ist, genügt es, das Verhalten für $x\to \infty$ zu betrachten. Für immer größer werdende Werte für $x$ wird $x^4$ auch immer größer. Da $x^4$ viel schneller wächst als $x^2$ bedeutet dies

$\lim\limits_{x\to\infty}f(x)=\lim\limits_{x\to-\infty}f(x)=„\infty“$.

Wenn du das Monotonieverhalten der Funktion sowie das Verhalten im Unendlichen gemeinsam betrachtest, kannst du den Wertebereich der Funktion $f(x)=0,2x^4-2x^2+3,2$ angeben: $\mathbb{W}_f=[-1,8;\infty]$.

Die Wendepunkte

Um eine Funktion auf Wendepunkte zu untersuchen, prüfst du ebenfalls eine notwendige und eine hinreichende Bedingung wie bei den Extrema. Bei den Wendepunkten benötigst du die zweite und dritte Ableitung. Diese sind

$f''(x)=2,4x^2-4$

sowie

$f''(x)=4,8x$.

Die notwendige Bedingung

Es muss gelten $f''(x)=0$, also $2,4x^2-4=0$.

• Addiere $4$ zu $2,4x^2=4$ und dividiere durch $2,4$. So erhältst du $x^2=\frac53$.
• Ziehe nun die Wurzel: $x_{W_1}=-\sqrt{\frac53}$ sowie $x_{W_2}=\sqrt{\frac53}$.

Auch bei den Wendepunkten musst du diese Stellen in der folgenden Ableitung einsetzen.

Die hinreichende Bedingung

Zusätzlich zu der notwendigen Bedingung muss $f'''(x_W)$ für die gefundenen Wendestellen gelten.

• $x_{W_1}=-\sqrt{-\frac53}$: $f'''\left(-\sqrt{\frac53}\right)=4,8\cdot\left(-\sqrt{\frac53}\right)\neq 0$.
• $x_{W_2}=-\sqrt{\frac53}$: $f'''\left(\sqrt{\frac53}\right)=4,8\cdot\left(\sqrt{\frac53}\right)\neq 0$.

Bestimmung der Wendepunkte

Zuletzt berechnest du die jeweiligen y-Koordinaten der Wendepunkte. Setze die Wendestellen in der Funktionsgleichung ein:

$f\left(-\sqrt{\frac53}\right)=0,2\left(-\sqrt{\frac53}\right)^4-2\left(-\sqrt{\frac53}\right)^2+3,2=\frac{19}{45}$

sowie

$f\left(\sqrt{\frac53}\right)=0,2\left(\sqrt{\frac53}\right)^4-2\left(\sqrt{\frac53}\right)^2+3,2=\frac{19}{45}$.

Damit sind die folgenden Punkte die Wendepunkte

$WP_1\left(-\sqrt{\frac53}\bigg\vert \frac{19}{45}\right);~WP_2\left(\sqrt{\frac53}\bigg\vert \frac{19}{45}\right)$.

Nun kannst du auch die Wendepunkte (blau) in das Koordinatensystem eintragen:

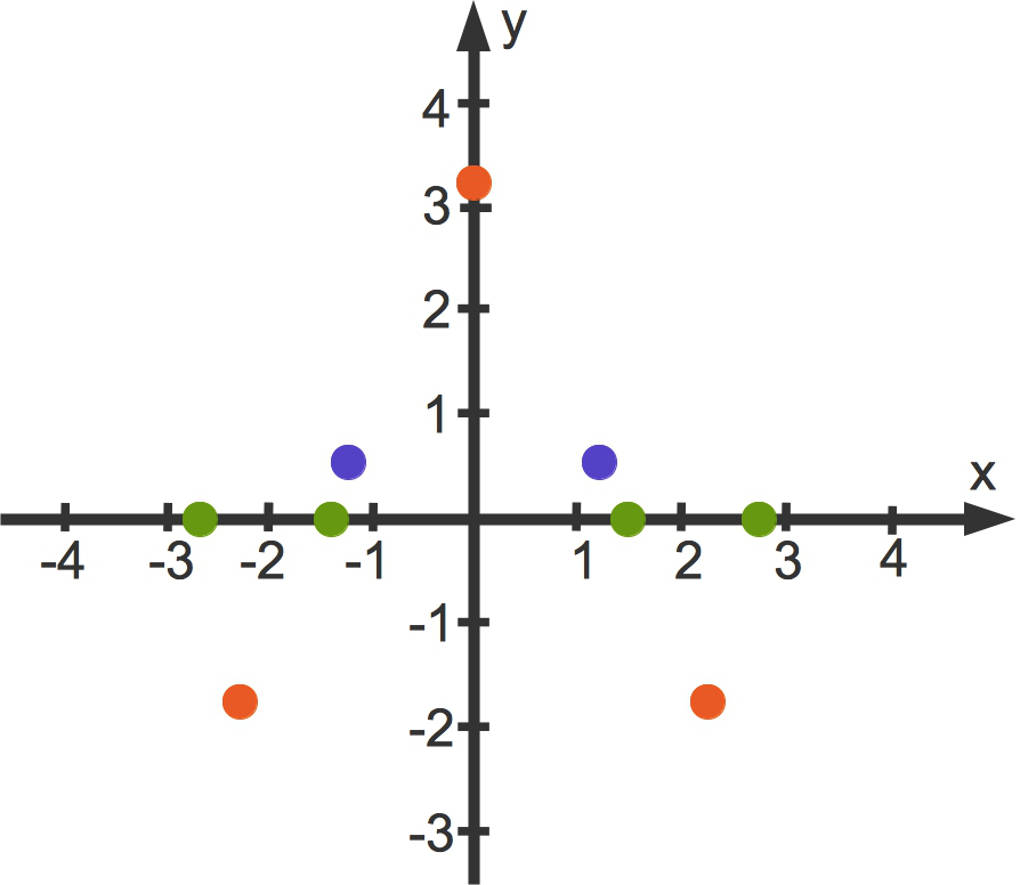
Der Graph der Funktion

Nun kannst du gegebenenfalls noch eine Wertetabelle erstellen und dann, gemeinsam mit den bereits berechneten Punkten, den Funktionsgraphen (rot) zeichnen.

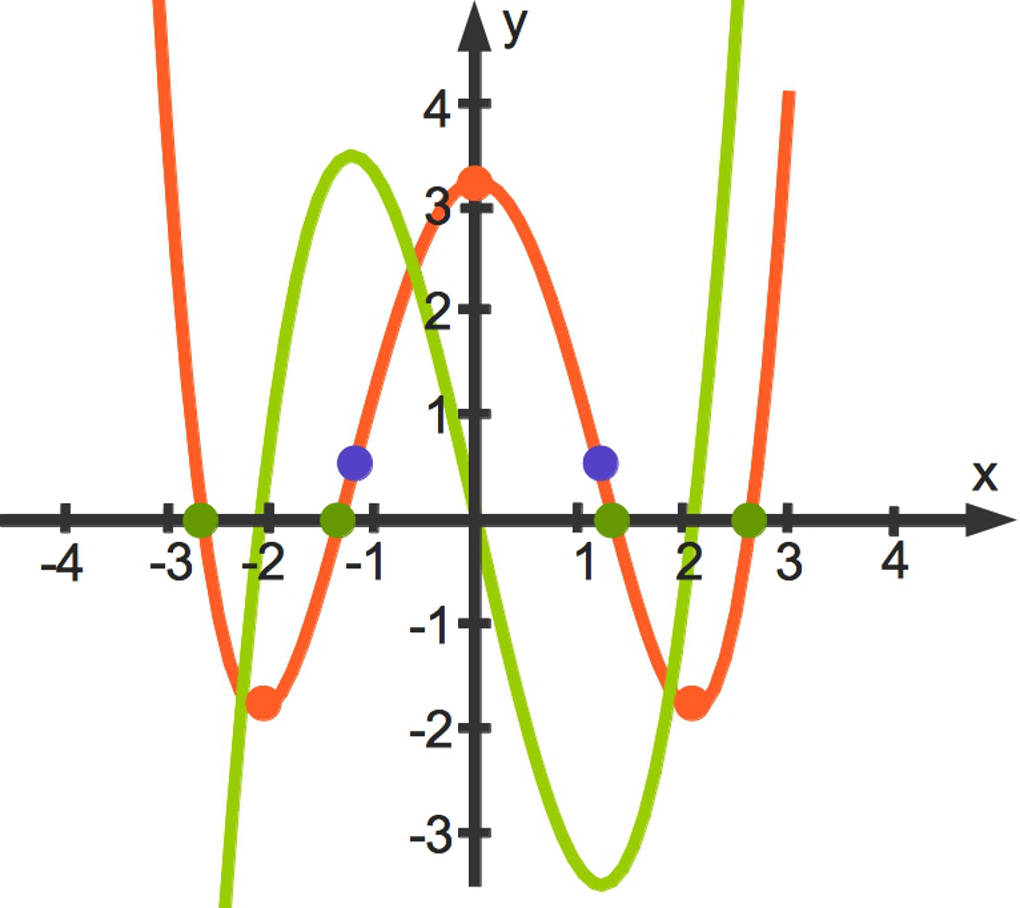
In dem gleichen Koordinatensystem siehst du auch noch den Graphen der Ableitungsfunktion (grün).

• Daran kannst du sofort erkennen, dass die Extremstellen der Funktion die Nullstellen der Ableitungsfunktion sind.
• In den Bereichen, in denen die Ableitungsfunktion positiv ist $(f'(x) > 0)$, ist die Funktion monoton wachsend. Wenn die Ableitungsfunktion negativ ist $(f'(x) < 0)$, ist die Funktion monoton fallend.
• Übrigens: Die Extremstellen der Ableitung sind die Wendestellen der Funktion.