Drei- und mehrstufige Zufallsexperimente
In der Stochastik betrachtest du den Zufall. Dabei geht es insbesondere darum, mit „Zufall zu rechnen“. Das bedeutet, dass du Wahrscheinlichkeiten berechnest.
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Was ist ein Zufallsexperiment?
- Baumdiagramme und Pfadregeln
- Beispiel 1: Die Augensumme bei dreimaligem Werfen mit einem Würfel
- Beispiel 2: Mehrmaliger Münzwurf
- Ausblick
Was ist ein Zufallsexperiment?
In der Stochastik beschäftigst du dich mit Zufallsexperimenten: Ein Zufallsexperiment ist ein spezielles Experiment. Dabei muss gelten, dass
- mindestens zwei Ergebnisse möglich sind,
- es beliebig oft durchgeführt werden kann und
- das Ergebnis nicht vorhersehbar ist.
Ein Ergebnis ist ein möglicher Ausgang dieses Zufallsexperimentes.
Du siehst, dass sich ein Zufallsexperiment zum Beispiel von einem physikalischen Experiment unterscheidet. Bei einem physikalischen Experiment soll unter gewissen Versuchsanordnungen ein vermutetes Ergebnis beobachtet werden. Das Ergebnis ist also vorhersehbar.
Beispiele für Zufallsexperimente sind:
- Das Werfen mit einem Spielwürfel. Du betrachtest dann als mögliche Ergebnisse die Augenzahlen von $1$ bis $6$.
- Das Werfen mit einer Münze. Hier betrachtest du die möglichen Ergebnisse „Kopf“ oder „Zahl“.
Du kannst einen Würfel oder eine Münze auch mehr als einmal hintereinander werfen. Die resultierenden Zufallsexperimente werden dann als mehrstufige (zweistufige, dreistufige, vierstufige, ...) Zufallsexperimente bezeichnet.
Baumdiagramme und Pfadregeln
Wie kannst du ein solches mehrstufiges Zufallsexperiment darstellen? Zur Darstellung von mehrstufigen Zufallsexperimenten verwendest du ein Baumdiagramm.
Ein solches Baumdiagramm schauen wir uns einmal am Beispiel eines zweistufigen Zufallsexperimentes an: Ein Würfel wird zweimal geworfen. Du notierst in der Reihenfolge der Würfe die Paare, welche aus den Augenzahlen in den einzelnen Würfen bestehen.
Zum Beispiel erhältst du für den ersten Wurf $3$ die folgenden Paare: $(3;1)$, $(3;2)$, $(3;3)$, $(3;4)$, $(3;5)$ sowie $(3;6)$
Wenn du ein Baumdiagramm zeichnest, kannst du erkennen, dass dieses sehr umfangreich wird. Hier siehst du einen Ausschnitt:
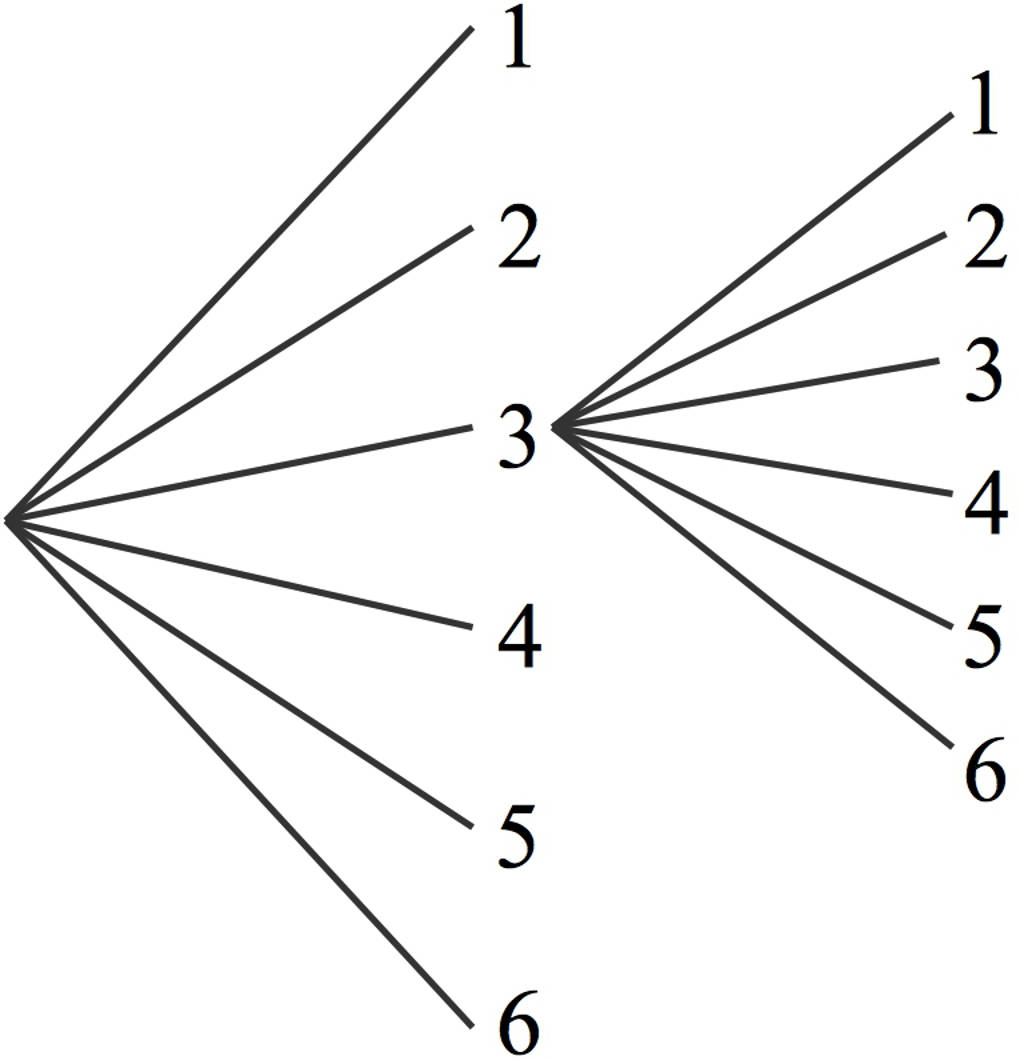
Was kannst du nun tun, wenn das Baumdiagramm zu umfangreich wird, weil ...
- ... entweder die Anzahl der möglichen Ergebnisse in jeder Stufe sehr groß ist
- ... oder die Anzahl der Stufen, also die Durchführungen des Experimentes, zu hoch ist?
Du kannst das jeweilige Baumdiagramm an die Aufgabenstellung anpassen, also vereinfachen. Man spricht dabei auch von reduzierten Baumdiagrammen.
Wir schauen uns nun Beispiele zu solchen vereinfachten Baumdiagrammen an.
Beispiel 1: Die Augensumme bei dreimaligem Werfen mit einem Würfel
Du würfelst dreimal mit einem handelsüblichen Spielwürfel.

Wie groß ist die Wahrscheinlichkeit dafür, dass die Summe der $3$ gewürfelten Augenzahlen maximal $4$ beträgt? Du könntest nun ein komplettes Baumdiagramm mit $6^{3}=216$ Pfaden zeichnen. Dann bist du allerdings reichlich beschäftigt. Überlege dir doch, welche Kombinationen zu der maximalen Augensumme führen: Eine $3$ oder eine größere Augenzahl fällt von vornherein aus. Die Summe wäre auf jeden Fall größer als $4$. Bleiben also nur noch die Augenzahlen $1$ und $2$. Du kannst nun ein vereinfachtes Baumdiagramm zeichnen:
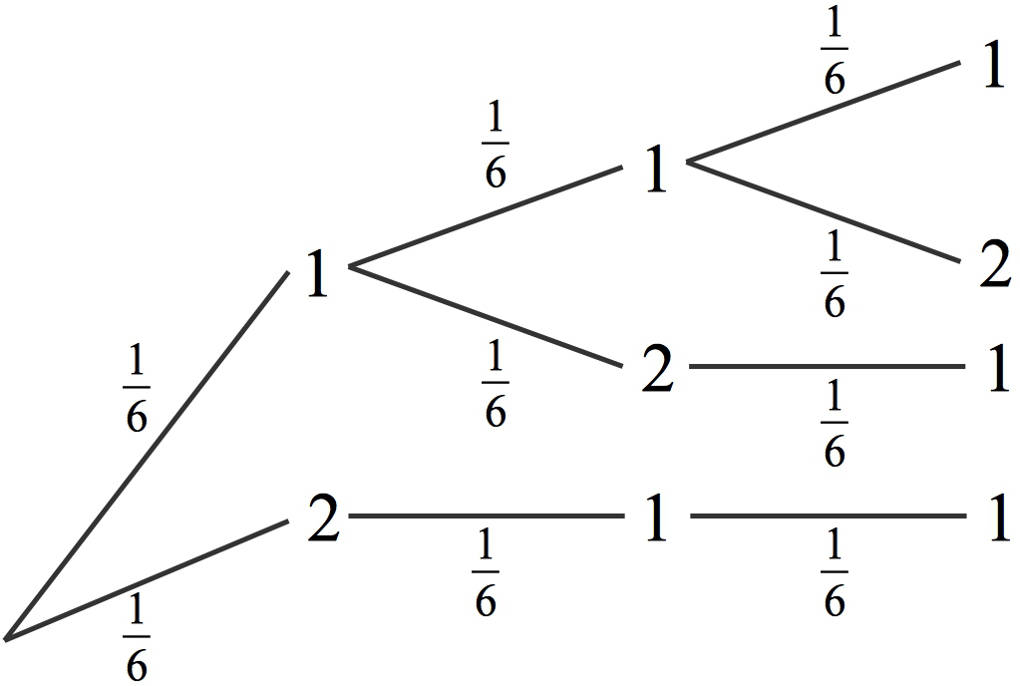
Wenn du im ersten Wurf eine $2$ hast, müssen die folgenden beiden jeweils eine $1$ sein. Hast du im ersten Wurf eine $1$, kann maximal einer der folgenden Würfe eine $2$ sein.
Auf den jeweiligen Ästen, die zu einem Ergebnis in einer Stufe führen, sind die Wahrscheinlichkeiten für das Eintreten dieses Ergebnisses notiert. Wie kannst du schließlich die Wahrscheinlichkeit des betrachteten Ereignisses „Augensumme maximal $4$“ berechnen?
Du verwendest die Pfadregeln:
- Die 1. Pfadregel oder auch Produktregel besagt, dass die Wahrscheinlichkeit eines Ergebnisses eines mehrstufigen Zufallsexperimentes das Produkt der Wahrscheinlichkeiten entlang des Pfades ist, der zu diesem Ergebnis führt.
- Die 2. Pfadregel oder auch Summenregel besagt, dass die Wahrscheinlichkeit eines Ereignisses die Summe der Wahrscheinlichkeiten aller Ergebnisse ist, die für das Ereignis günstig sind.
So ergibt sich hier:
$P(\text{„Augensumme maximal $4$“})=4\cdot \left(\frac16\right)^3=\frac1{54}\approx 1,85\%$
Beispiel 2: Mehrmaliger Münzwurf
Du wirfst eine Münze sechsmal. Wie groß ist die Wahrscheinlichkeit, dass genau einmal „Kopf“ vorkommt? Auch hier wäre das Baumdiagramm mit $2^{6}=64$ Pfaden sehr umfangreich.
Wir schauen uns zunächst ein Ergebnis an, ein sogenanntes $6$-Tupel, in welchem einmal „Kopf“ vorkommt. Wird „Kopf“ mit $\text{K}$ und „Zahl“ mit $\text{Z}$ abgekürzt, so ist $(\text{K};\text{Z};\text{Z};\text{Z};\text{Z};\text{Z})$ ein mögliches Ergebnis. Es gibt noch weitere solche $6$-Tupel, in welchen $\text{K}$ einmal vorkommt. Es könnte an der zweiten, der dritten, der vierten, der fünften und an der sechsten Stelle vorkommen. Es gibt also $6$ solcher $6$-Tupel. Die Wahrscheinlichkeit ist jedes Mal $\left(\frac12\right)^{6}$. So erhältst du insgesamt folgende Wahrscheinlichkeit:
$P(\text{„genau einmal Kopf“})=6\cdot \left(\frac12\right)^6=\frac3{32}=9,375\%$
Weitere Beispiele findest du hier:
Ausblick
Wenn du sogenannte Punkt- oder Intervallwahrscheinlichkeiten berechnen sollst und das Zeichnen eines Baumes zu umfangreich wird, unterscheidest du wie folgt:
- Urnenmodelle mit Zurücklegen: Hier verwendest du die Formel von Bernoulli oder auch die Binomialverteilung.
- Urnenmodelle ohne Zurücklegen: Hier verwendest du die hypergeometrische Verteilung, welche du auch häufig unter dem Namen Lottomodell findest.
Alle Videos und Lerntexte zum Thema
Videos und Lerntexte zum Thema
Drei- und mehrstufige Zufallsexperimente (4 Videos, 1 Lerntext)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Drei- und mehrstufige Zufallsexperimente (3 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung





 Mehrstufige Zufallsexperimente
Mehrstufige Zufallsexperimente
 Bernoulli-Experimente und Bernoulli-Ketten
Bernoulli-Experimente und Bernoulli-Ketten
 Mindestwahrscheinlichkeiten
Mindestwahrscheinlichkeiten









