Grafisches Ableiten
- Grafisches Ableiten – Einführung
- Steigung und Tangente – die Grundlagen
- Wichtige Zusammenhänge beim grafischen Differenzieren
- Grafisches Ableiten – Schritt für Schritt
- Grafisches Ableiten – Beispiel


in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
Grundlagen zum Thema Grafisches Ableiten
Grafisches Ableiten – Einführung
Beim grafischen Ableiten lernst du, wie du direkt aus dem Graphen einer Funktion $f(x)$ den Graphen ihrer Ableitungsfunktion $f'(x)$ herleiten und skizzieren kannst.
Definition: Die grafische Ableitung (auch grafisches Differenzieren genannt) beschreibt ein Verfahren, bei dem anhand des Verlaufs einer Funktion $f(x)$ der Graph der Ableitungsfunktion $f'(x)$ gezeichnet wird.
Steigung und Tangente – die Grundlagen
Die Ableitung einer Funktion gibt die Steigung der am Graphen anliegenden Tangente und somit auch die Steigung des Funktionsgraphen selbst an jedem Punkt an.
- Verläuft die Tangente steigend, ist $f'(x) > 0$.
- Verläuft die Tangente fallend, ist $f'(x) < 0$.
- Ist die Tangente waagerecht, gilt $f'(x) = 0$.
Ein Beispiel aus dem Alltag: Wenn du beim Fahrradfahren bergauf fährst, ist die Steigung positiv. Auf flacher Strecke ist sie null und bergab wird sie negativ.
Wichtige Zusammenhänge beim grafischen Differenzieren
Um den Ableitungsgraphen $f'$ eines gegebenen Funktionsgraphen $f$ zu zeichnen, helfen dir diese Grundregeln:
| $f(x)$ (Ausgangsfunktion) | $f'(x)$ (Ableitung) |
|---|---|
| Extrempunkt (Hoch-/Tiefpunkt) | Nullstelle |
| Wendepunkt | Extrempunkt |
| Steigung positiv | oberhalb der x-Achse |
| Steigung negativ | unterhalb der x-Achse |
Merke: Nullstellen von $f'(x)$ liegen genau dort, wo $f(x)$ einen Hoch- oder Tiefpunkt hat!
Grafisches Ableiten – Schritt für Schritt
So gehst du beim Zeichnen des Ableitungsgraphen vor:
- Lokalisiere die Extrempunkte von $f(x)$ → Markiere die Nullstellen von $f'(x)$ bei den entsprechenden $x$-Werten.
-
Schaue auf die Steigung zwischen diesen Punkten:
- Steigend → $f'(x) > 0$
- Fallend → $f'(x) < 0$
-
Lokalisiere Wendepunkte von $f(x)$ → Zeichne an diesen Stellen Extrempunkte in $f'(x)$.
(Profitipp: Wenn du relativ genau skizzieren möchtest, schätze die Steigung an der Wendestelle ab, um den Funktionswert des Extrempunkts von $f'(x)$ ungefähr richtig einzeichnen zu können.) - Zeichne den Verlauf des Ableitungsgraphen entsprechend grob ein, indem du die bekannten Punkte zu einem glatten Kurvenverlauf verbindest.
Grafisches Ableiten – Beispiel
Schau dir den Verlauf dieses Funktionsgraphen als Beispiel an.
Zuerst markierst du alle Extremstellen des Funktionsgraphen (mit waagerechten Tangenten) als Nullstellen der Ableitung:
- $x = -5$
- $x = -3$
- $x = 1$
Zweitens betrachtest du die Steigung auf verschiedenen Intervallen. Da der Graph von $f(x)$ für $x \lt -5$ fällt, hat die Ableitung hier negative Funktionswerte. Das Gleiche gilt für den Bereich zwischen $x=-3$ und $x=1$. Für den Bereich zwischen $x=-5$ und $x=-3$ sowie für $x > 1$ hat die Ableitung positive Werte.
Nun kannst du noch die Punkte, an denen sich die Krümmung des Graphen von $f(x)$ ändert (die Wendestellen), als Extrempunkte der Ableitung kennzeichnen. Wenn du relativ genau sein möchtest, musst du an diesen Stellen noch die Steigung von $f(x)$ abschätzen.
Abschließend ziehst du eine durchgehende Kurve durch die markierten Nullstellen mit Extrempunkten an den entsprechenden Stellen.
Fehleralarm Viele verwechseln den $y$-Wert der Ausgangsfunktion mit dem Funktionswert der Ableitung. Achte darauf: Für die Ableitung ist nicht der Funktionswert von $f(x)$ entscheidend, sondern die Steigung an dieser Stelle!
Grafisches Ableiten – Wissens-Check
Ausblick – das lernst du nach dem grafischen Ableiten
Wenn du das Thema üben möchtest, schau doch mal bei den Übungen zum grafischen Ableiten vorbei!
Wenn du das grafische Ableiten verstanden hast, kannst du dich im nächsten Schritt mit dem analytischen Ableiten beschäftigen. Dabei lernst du, Ableitungen mit festen Rechenregeln zu bestimmen. Außerdem ist Wissen zum Skizzieren von Funktionsgraphen für die Kurvendiskussion nützlich, bei der Monotonie, Krümmung und Extremstellen einer Funktion exakt analysiert werden.
Zusammenfassung zum Thema Grafisches Ableiten
- Beim grafischen Ableiten leitest du aus dem Graphen von $f$ den grafischen Verlauf von $f'$ her.
- Stellen, an denen $f$ Extrempunkte hat, sind Nullstellen von $f'$.
- An Stellen, an denen $f$ Wendepunkte hat, hat $f'$ Extrempunkte.
- In Bereichen von $f$, in denen die Steigung positiv ist, verläuft $f'$ oberhalb der $x$-Achse.
- In Bereichen von $f$, in denen die Steigung negativ ist, verläuft $f'$ unterhalb der $x$-Achse.
Häufig gestellte Fragen zum Thema Grafisches Ableiten
Transkript Grafisches Ableiten
Hallo, schön, dass du mal wieder da bist! Heute wirst du lernen, wie man aus dem Graphen einer Funktion den Graphen ihrer Ableitungsfunktion herleiten kann. Du wirst sehen, dass man dazu gar nicht die Funktionsgleichung benötigst. Du wirst in diesem Video also lernen, grafisch abzuleiten.
Steigung des Graphen f
Wie du sicherlich weißt, gibt die Ableitung an einer Stelle die Steigung der zugehörigen Funktion an dieser Stelle an. Dabei müssen wir verschiedene Sachverhalte betrachten:
Zunächst einmal ist die Steigung des Ursprungsgraphen f von besonderen Interesse. Ist die Steigung von f positiv, dann verläuft der Graph der Ableitungsfunktion f Strich natürlich oberhalb der x-Achse, da die Steigung von f ja positiv ist. Natürlich gilt auch der umgekehrte Fall, ist die Steigung von f negativ, dann verläuft der Graph der Ableitungsfunktion f Strich unterhalb der x-Achse.
Dies möchte ich an einem Beispiel erklären. Du siehst hier den Funktionsgraphen der Funktion f(x) = 4 x². Zunächst fällt der Graph bis zur Extremstelle x = 0. Danach steigt der Funktionsgraph an.
Wenn man nun den Graphen der Ableitungsfunktion f' anschaut, so sieht man, dass er bis zur Extremstelle x = 0 unterhalb der x-Achse verläuft und danach oberhalb der x-Achse verläuft. Dies ist deshalb der Fall, da der Graph der Ursprungsfunktion nach der Extremstelle ansteigt.
Extremstellen des Graphen f
Neben der Steigung sind auch die Extremstellen charakteristisch und helfen uns beim Zeichnen des Graphen der Ableitungsfunktion.
An jeder Extremstelle einer Funktion – also einem Hoch- oder Tiefpunkt – beträgt die Steigung 0. Deshalb hat an diesen Stellen die Ableitungsfunktion f' ihre Nullstellen.
Schauen wir uns dies einmal an einem Beispiel genauer an. Der rote Funktionsgraph stellt hier die Gleichung f(x) = x hoch 4 − 2x² dar. Der blaue Funktionsgraph stellt die dazugehörige Ableitungsfunktion f strich dar
Unsere Ursprungsfunktion hat drei Extremstellen. Schau einmal genau hin: Denn an genau diesen Stellen hat der Graph der Ableitungsfunktion seine Nullstellen.
Weißt du auch noch, warum? Richtig. Weil die Ableitungsfunktion f' die Steigung der Funktion f abbildet und die Steigung von f an Extremstellen null ist.
Indem du also die Steigung und Extremstellen einer Funktion beachtest, kannst du den Graphen ihrer Ableitungsfunktion zeichnen. Dies möchte ich dir nun abschließend an einem letzten Beispiel wiederholen.
Beispiel Graphen der Ableitungsfunktion zeichnen
Hier siehst du den Graphen einer gewöhnlichen Parabel. Die Funktionsgleichung interessiert uns beim grafischen Ableiten nicht. Welche Merkmale helfen uns nun aber dabei, die Parabel grafisch abzuleiten.
Als erstes müsste dir der Tiefpunkt der Parabel auffallen. An dieser Stelle hat die Ableitungsfunktion also einen Nullpunkt. Da die Steigung der Parabel links vom Tiefpunkt negativ ist, befinden sich die Funktionswerte der Ableitungsfunktion links der Nullstelle unterhalb der x-Achse.
Und da die Steigung der Parabel rechts vom Tiefpunkt positiv ist, befinden sich die Funktionswerte der Ableitungsfunktion rechts der Nullstelle überhalb der x-Achse.
Da es sich beim Graphen der Ursprungsfunktion um eine Parabel handelt - also um eine quadratische Funktion – , ist der Graph der Ableitungsfunktion eine Gerade – also eine lineare Funktion.
Nun kennst du die beiden wichtigsten Sachverhalte auf die du beim graphischen differenzieren achten musst: die Steigung und die Extremstellen der Ursprungsfunktion. Wenn du die Regeln befolgst, so wirst du den Graph der Ableitungsfunktion sicher zeichnen können.
Ich hoffe, dass es dir Spaß gemacht hat ! Wir sehen uns bestimmt bald wieder.
Grafisches Ableiten Übung
-
Bestimme die Anzahl der Nullstellen von $f'$.
TippsDie Steigung von $f$ bestimmt das Vorzeichen von $f'$:
$\begin{array}{c|c} f(x)&f'(x) \\ \hline \text{positive Steigung}&f'(x)>0 \\ \hline \text{negative Steigung}&f'(x)<0 \end{array}$
Die Steigung in einem Extrempunkt ist immer $0$. Dort hat die Ableitungsfunktion also eine Nullstelle.
Zähle die Anzahl der Extrempunkte.
LösungDa die Steigung von $f$ an jeder Stelle den Verlauf von $f'$ bestimmt, sind Nullstellen von $f'$ ein ganz besonderer Fall.
Denn $f'$ besitzt nur dort Nullstellen, wo $f$ eine Steigung von $0$ aufweist.
Das ist nur in Extrempunkten der Fall. Wie wir sehen, besitzt der Graph von $f$ genau zwei Tiefpunkte und einen Hochpunkt. Damit muss der Graph der Ableitungsfunktion genau an diesen Stellen Nullstellen besitzen.
-
Bestimme den Graphen der Ableitungsfunktion.
TippsDer Zusammenhang zwischen der Steigung der Ausgangsfunktion und dem Graphenverlauf der Ableitungsfunktion lautet:
$\begin{array}{c|c} f(x)&f'(x) \\ \hline \text{positive Steigung}&f'(x)>0 \\ \hline \text{negative Steigung}&f'(x)<0 \end{array}$
Bei einem Extrempunkt der Ausgangsfunktion besitzt die Ableitungsfunktion eine Nullstelle.
Die Funktionsgleichung lautet $f(x)=(x-1)^2+1$. Diese könntest du auch alternativ rechnerisch ableiten.
LösungDer Graph der Ableitungsfunktion gibt uns Informationen über die Steigung und Extrema der Ausgangsfunktion.
Da die Ausgangsfunktion $f$ einen Tiefpunkt hat, muss der Graph der Ableitung dort eine Nullstelle besitzen. Das trifft nur auf drei der Graphen zu. Übrig bleiben also nur noch die Graphen 1, 3 und 4.
Das nächste Kriterium ist die Steigung von $f$. Bis zum Tiefpunkt fällt $f$, d.h., dort müsste seine Ableitung im negativen Bereich verlaufen.
Das trifft nur auf den Graphen 3 zu. Was wir hier gemacht haben, nennt sich grafisches Ableiten: Wir bestimmen den Graphen der Ableitungsfunktion allein anhand des Verlaufes der Ursprungsgraphen, ohne zu rechnen.
Alternativ kannst du natürlich auch rechnen. Wir kennen die Funktionsgleichung $f(x)=(x-1)^2+1$, was man beispielsweise an der Lage des Scheitelpunktes erkennen. Diese lösen wir jetzt mit Hilfe der zweiten binomischen Formel ein wenig auf und leiten sie dann ab:
$f(x)=x^2 - 2x + 1 + 1$
$f'(x)=2x-2$.
Da der Ableitungsgraph einer Parabel immer eine Gerade ist, können wir den Schnittpunkt mit der y-Achse ablesen. Dieser müsste bei $(0|-2)$ liegen, was nur auf den dritten Graphen zutrifft.
-
Entscheide, in welchen Diagrammen die Funktion und ihre Ableitungsfunktion dargestellt sind.
TippsBei Extrempunkten der Ausgangsfunktion besitzt die Ableitungsfunktion immer eine Nullstelle.
Fällt der Graph von $f$, verläuft der Ableitungsgraph im negativen Bereich.
Zwei der angegebenen Diagramme zeigen eine Funktion und ihre Ableitungsfunktion.
LösungGehen wir die Graphen der Reihe nach durch.
Beim ersten Bild ist die Parabel nach unten geöffnet. Ihre Steigung bis zum Hochpunkt ist positiv, weshalb der Ableitungsgraph in diesem Bereich noch positiv verlaufen müsste. Da er aber im negativen Bereich ist, kann das kein Ableitungsgraph zur Ursprungsfunktion sein.
Beim zweiten Bild ist es ähnlich: Die Steigung der Parabel ist bis zum Tiefpunkt negativ. Hier müsste der Ableitungsgraph also im negativen Bereich verlaufen. Da er sich im positiven Bereich befindet, ist auch das kein Ableitungsgraph zur Ursprungsfunktion.
In Bild $3$ sehen wir eine negative Steigung der Parabel bis zum Tiefpunkt. Dort verläuft die Gerade im negativen Bereich. Ab dem Tiefpunkt beginnt die Parabel positiv zu steigen und auch die Gerade verläuft ab hier im positiven Bereich. So weit so gut. Auch die Nullstelle, die der Ableitungsgraph bei jedem Extrempunkt der Ausgangsfunktion besitzen muss, ist an der richtigen Stelle vorhanden. Dies ist der Ableitungsgraph zur vorgegebenen quadratischen Funktion.
Im letzten Bild verhält es sich genauso wie in Bild $3$. Diesmal sind Parabel und Gerade nur weiter nach rechts verschoben. Es sind also wieder die Graphen einer Funktion und ihrer Ableitungsfunktion dargestellt.
-
Ordne den Funktionsgraphen den Graph ihrer Ableitungsfunktion zu.
TippsEin Hinweis zum Graphenverlauf der Ableitungsfunktion im Bezug auf die Steigung $m$ der Ausgangsfunktion:
$\begin{array}{c|c} f(x)&f'(x) \\ \hline \text{positive Steigung}&f'(x)>0 \\ \hline \text{negative Steigung}&f'(x)<0 \end{array}$
Bei einem Extrempunkt der Ausgangsfunktion besitzt die Ableitungsfunktion eine Nullstelle.
Hier ein Beispiel für eine Parabel und die Gerade ihrer Ableitungsfunktion.
LösungFangen wir mit dem einfachsten Bild an: die Parabel, die nach unten geöffnet ist. Ihr Partner muss die in ihrer Steigung fallende Gerade sein, weil Geraden immer die Ableitungsgraphen von Parabeln bilden.
Als nächstes die Funktion, die nur steigt und durch den Ursprung verläuft. Da ihre Steigung immer positiv ist, muss der Graph ihrer Ableitung komplett im positiven Bereich liegen. Das trifft nur auf die Parabel zu.
Nun kommen wir zu der Funktion, die erst einen Hochpunkt und kurz darauf einen Tiefpunkt im Ursprung besitzt. Ihr Ableitungsgraph muss also an diesen Stellen Nullstellen aufweisen. Es bleibt nur noch ein Graph mit zwei Nullstellen übrig.
Das letzte Pärchen ergibt sich von selbst: Übrig bleibt die Ausgangsfunktion in Form eines W, mit drei Extrempunkten. Der letzte Partner, der in Frage kommt, besitzt passend dazu drei Nullstellen.
Du kannst statt der Nullstellen auch die Steigung der Ausgangsfunktion mit der Lage des Ableitungsgraphen an diesen Stellen vergleichen, denn diese verhalten sich immer so:
$\begin{array}{c|c} f(x)&f'(x) \\ \hline \text{positive Steigung}&f'(x)>0 \\ \hline \text{negative Steigung}&f'(x)<0 \end{array}$
-
Vervollständige die Aussagen zum Graphen der Ableitungsfunktion.
TippsDie Steigung von $f$ bestimmt das Vorzeichen der Ableitungsfunktion $f'$:
$\begin{array}{c|c} f(x)&f'(x) \\ \hline \text{positive Steigung}&f'(x)>0 \\ \hline \text{negative Steigung}&f'(x)<0 \end{array}$
Bei Extrempunkten der Ausgangsfunktion weist die Ableitungsfunktion immer eine Nullstelle auf.
LösungIm Bild siehst du die Ausgangsfunktion und ihre dazugehörige Ableitungsfunktion.
Der Graph der Ableitung ist eine Gerade. Links von der y-Achse verläuft sie im negativen Bereich, da die Ausgangsfunktion dort eine negative Steigung besitzt.
Im Ursprung des Koordinatensystems hat der Graph von $f$ einen Tiefpunkt, also dort ist die Steigung $0$. Deshalb besitzt $f'$ dort eine Nullstelle.
Nach dem Tiefpunkt wird die Steigung der quadratischen Funktion positiv, weshalb auch $f'$ ab dort im positiven Bereich verläuft.
-
Ermittle die richtigen Eigenschaften von $f'$ anhand des vorgegebenen Graphens $f$.
TippsDie Steigung von $f$ bestimmt das Vorzeichen von $f'$:
$\begin{array}{c|c} f(x)&f'(x) \\ \hline \text{positive Steigung}&f'(x)>0 \\ \hline \text{negative Steigung}&f'(x)<0 \end{array}$
Eine Definitionslücke des Ausgangsgraphen bedeutet ebenfalls eine Definitionslücke beim Ableitungsgraphen.
Ob die Ableitungsfunktion wächst oder nicht, kannst du gedanklich nachvollziehen, wenn du eine Tangente an den Graphen legst und die Steigung der Tangente betrachtest.
Der Graph gehört zu der Funktion
$f(x)=\frac{1}{x}$.
Die Ableitungsfunktion lautet
$f'(x)=-\frac{1}{x^2}$.
LösungDu siehst im Bild den Graphen zur Ableitungsfunktion $f'$.
Er verläuft komplett unterhalb der x-Achse, also im negativen Bereich. Das ist deshalb so, weil der Ausgangsgraph permanent fällt, d.h., immer eine negative Steigung aufweist.
Die Definitionslücke behält der Ableitungsgraph auch bei.
Der Graph zu $f$ besitzt - auch wenn es vielleicht so aussehen mag - keinerlei Extrempunkte. Folglich kann der Ableitungsgraph auch keine Nullstellen haben.
Der Graph von $f'$ fällt zunächst und steigt danach, was man gedanklich nachvollziehen kann, wenn man eine Tangente an den Graphen des Ursprungsgraphen legt und die Steigung der Tangente betrachtet. Der Anstieg ist zunächst relativ gering und wird sehr schnell größer, je weiter man sich von links der Definitionslücke nähert. Der Anstieg wird dann wieder geringer, je weiter man nach rechts geht.
9.711
sofaheld-Level
6.600
vorgefertigte
Vokabeln
8.276
Lernvideos
38.589
Übungen
33.616
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Klassenstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung


 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?





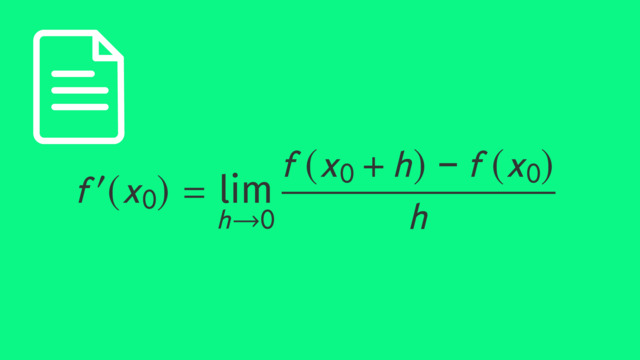












Hallo, ich fand das Video sehr hilfreich :D
Unter der Überschrift "Graphisches Ableiten" erwarte ich eigentlich, dass hier ausschließlich Aspekte des Graphen behandelt werden.
Nur so können die zentralen Aspekte dieses Themas klar herausgearbeitet werden.
Die hier genannten Beispiele mit konkreten Funktionstermen sind leider nicht optimal für dieses Thema geeignet.
Statt dessen sollte man Kurvenverläufe wählen, deren Funktionsterme völlig unbekannt sind.
Beste Grüße aus Bremen
Jan Arndt
Hallo Felix G.,
entschuldige bitte die sehr verspätete Antwort!
In diesem Video geht es um das graphische Ableiten, sprich wie man sich überlegen kann, wie der Graph der Ableitungsfunktion aussieht, wenn man nur den Ursprungsgraphen gegeben hat. Bestimmtes Vorwissen, was zu einem früheren Zeitpunkt in der Schule bereits behandelt wurde, wird dabei vorausgesetzt.
Zur Steigung einer Geraden gibt es bei uns noch andere Videos. Schau doch zum Beispiel mal hier rein: https://www.sofatutor.com/mathematik/videos/steigung-proportionaler-funktionen-steigungsdreiecke
Oder auch hier:
https://www.sofatutor.com/mathematik/videos/lineare-funktionen-steigung-3
Liebe Grüße aus der Redaktion
Du hättest die Steigung der Geraden erklären sollen, d.h., wie man darauf kommt?
Danke hat mir sehr geholfen😊