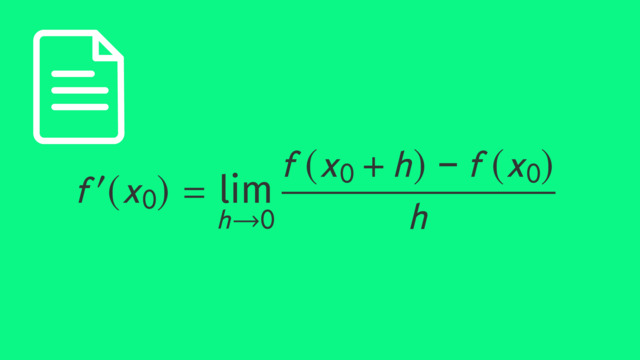Ableitungsfunktion – Steigung einer Funktion an einer beliebigen Stelle
Die Ableitungsfunktion hilft uns dabei, die Geschwindigkeit von Skispringern während ihres Sprungs zu berechnen. Lerne, wie man die Ableitungsfunktion bestimmt, um die momentane Geschwindigkeit zu ermitteln. Interessiert? All das und mehr findest du im folgenden Video!
in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
5 Minuten verstehen
5 Minuten üben
2 Minuten Fragen stellen
Bereit für eine echte Prüfung?
Grundlagen zum Thema Ableitungsfunktion – Steigung einer Funktion an einer beliebigen Stelle
Die Ableitungsfunktion in Mathe
Skispringer können während eines Sprungs sehr hohe Geschwindigkeiten erreichen. Aber wie schnell werden sie genau? Wenn man die Funktion kennt, die die Flugbahn beschreibt, kann man die Ableitung nutzen, um etwas über die Geschwindigkeit herauszufinden. Daher beschäftigen wir uns im Folgenden mit der Ableitungsfunktion.
Ableitungsfunktion – Erklärung
Wir nehmen an, dass wir die Funktion $s(t)$ kennen, mit der die zurückgelegte Strecke während eines Sprungs beschrieben wird. Diese Funktion lautet:
$s(x) = 2,6 \cdot \pu{m//s^{2}} \cdot x^{2}$
Dabei ist $x$ in der Einheit Sekunden gegeben. Wir wissen schon, wie wir die mittlere oder durchschnittliche Geschwindigkeit zwischen zwei Zeitpunkten mithilfe des Differenzenquotienten bestimmen können. Dazu verwenden wir das Steigungsdreieck der Funktion und berechnen den Quotienten der Differenzen, eben den Differenzenquotienten: $\frac{\Delta y}{\Delta x}$. Die momentane Geschwindigkeit zu einem Zeitpunkt $x_0$ ist der Grenzwert des Differenzenquotienten für sehr kleine Differenzen: $v(x_0) = s^{\prime}(x_0)$. Er ist allgemein folgendermaßen definiert:
$f^{\prime}(x_0) = \lim\limits_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = \lim\limits_{h \to 0} \frac{ f(x_0+h)-f(x_0) }{ h }$
Dabei entspricht $h$ der Breite von $\Delta x$. Wir könnten nach dieser Methode die Steigung, also die Geschwindigkeit während des Sprungs, für jeden beliebigen Zeitpunkt $x_0$ berechnen. Wenn wir die Geschwindigkeit allerdings zu vielen oder allen Zeitpunkten des Sprungs herausfinden möchten, können wir einen effizienteren Weg wählen. Dazu berechnen wir den Differentialquotienten für $x_0$, ohne einen expliziten Wert einzusetzen.
Ableitungsfunktion bestimmen
Wir lassen an dieser Stelle die Einheiten weg und berechnen den Differentialquotienten für die Funktion $s(x) = 2,6x^{2}$ an der Stelle $x_0$:
$s^{\prime}(x_0)= \lim\limits_{h \to 0} \frac{ s(x_0+h)-s(x_0) }{ h }$
$s^{\prime}(x_0)= \lim\limits_{h \to 0} \frac{ 2,6(x_0+h)^{2} - 2,6(x_0^{2}) }{ h }$
Wir klammern die binomische Formel aus und lösen im Anschluss die Klammer auf:
$s^{\prime}(x_0)= \lim\limits_{h \to 0} \frac{ 2,6x_0^{2} +5,2x_0h + 2,6h^{2} -2,6x_0^{2} }{ h } $
Die Terme $ 2,6x_0^{2}$ und $ - 2,6x_0^{2}$ heben sich gegenseitig auf. Damit haben wir:
$s^{\prime}(x_0)= \lim\limits_{h \to 0} \frac{ 5,2x_0h+2,6h^{2} }{ h }$
Jetzt können wir $h$ kürzen und es bleibt:
$s^{\prime}(x_0)= \lim\limits_{h \to 0} ~ 5,2x_0 +2,6h$
Da $h$ gegen null läuft, läuft auch $2,6h$ gegen null. Damit erhalten wir schließlich:
$s^{\prime}(x_0) = 5,2x_0$
Das ist die Ableitungsfunktion der Funktion $s$. Wir können jeden beliebigen Wert (aus dem Definitionsbereich) einsetzen, um die Steigung der Funktion $s$ an dieser Stelle zu bestimmen. Oder, bezogen auf unser Beispiel, die Geschwindigkeit der Skispringer. Damit können wir auch eine Definition aufschreiben.
Ableitungsfunktion – Definition
Die Funktion $f$ sei auf dem Intervall $I$ definiert und $x_0 \in I$. Wenn der Grenzwert des Differenzenquotienten
Wenn du wie oben beschrieben die Differenzialquotienten von $f$ für beliebige Werte $x_0$ berechnest, ohne bereits einen Wert für $x_0$ einzusetzen, so erhältst du die Ableitungsfunktion $f^{\prime}$ der Funktion $f$. Im Beispiel ist $s^{\prime}(x) = 5,2 x$ die Ableitungsfunktion der Funktion $s(x) = 2,6 x^{2}$.
Ableitungsfunktion - Zusammenfassung
In diesem Video wird erklärt, was eine Ableitungsfunktion ist und wie sie mit dem Differenzenquotienten zusammenhängt. Im Video werden Beispiele berechnet. Neben Text und Video findest du Aufgaben und Übungen, um dein Wissen über die Ableitungsfunktionen zu vertiefen.
Transkript Ableitungsfunktion – Steigung einer Funktion an einer beliebigen Stelle
Wir schreiben das 17. Jahrhundert. Es ist der ultimative Showdown zwischen zwei der weltbesten Mathematiker. Eines der epischsten Mathe-Battles ever - Isaac Newton vs. Gottfried Wilhelm Leibniz. Beide entwickelten fast zeitgleich und unabhängig voneinander die Differentialrechnung. Aber teilen wollten sie sich die Ehre nicht. Worum es geht? Um Methoden zur „Bestimmung der Steigung von Funktionen an einer beliebigen Stelle“. Bisher wissen wir schon, dass wir mit dem Grenzwert der Sekantensteigungen, also dem Differentialquotienten, die Steigung einer Funktion an einer konkreten Stelle „x-null“ berechnen können. Zum Beispiel bei der Normalparabel, an der Stelle zwei. Da wir hier zwei nicht direkt einsetzen dürfen, weil wir dann durch Null teilen würden, müssen wir den Term geschickt umformen. Mit Hilfe der dritten binomischen Formel, und geschicktem Kürzen, können wir den Term so weit vereinfachen, dass wir „x-null“ einfach einsetzen und so die Steigung an dieser Stelle berechnen können. Ist ja ganz nett, diese Methode, aber es ist doch ein ziemlich großer Aufwand, den Grenzwert für jede einzelne Stelle zu berechnen. Viel einfacher ist es, wenn wir eine neue Funktion entwickeln, bei der wir jede beliebige Stelle nur noch einsetzen müssen und direkt die Steigung an dieser Stelle ermitteln könnten. Solch eine Funktion nennen wir „Ableitung“. Dafür verankern wir den Punkt P nicht an einer konkreten Stelle, sondern setzen ihn an eine beliebige Stelle x-null. Dann brauchen wir noch einen Punkt Q an einer zweiten Stelle x, den wir auf P zuwandern lassen, damit aus der Sekante eine Tangente wird. Das heißt, wir lassen x gegen x-null laufen. Dadurch wird die Differenz „x minus x-null“ unendlich klein, aber das Prozedere kennen wir ja schon von unserem Differentialquotienten. Diese sogenannte x-Methode, schauen wir uns jetzt anhand der Normalparabel genauer an. Anstatt also hier eine konkrete Stelle einzusetzen, lassen wir „x-null“ allgemein und formen nur die Funktionswerte entsprechend um. Die Differenz im Zähler können wir wieder mit der dritten binomischen Formel umformen, um dann zu kürzen. Wenn nun x gegen x-null läuft, erhalten wir als Summe zwei x-null. Da wir die Stelle x-null allgemein gelassen haben, gilt die Funktion „zwei x-null“ für jede beliebige Stelle x-null. Dann können wir auch die Null wieder wegnehmen und erhalten als Ableitungsfunktion der Normalparabel „zwei x“. Damit können wir nun die Steigung der Funktion an jeder Stelle berechnen, indem wir den entsprechenden Wert einfach in die Ableitungsfunktion einsetzen. Manchmal ist es jedoch nicht ganz so einfach, die Differenz im Nenner zu kürzen, deshalb gibt es neben der x-Methode auch die h-Methode. Hier schauen wir uns zur Abwechslung mal nicht die Normalparabel „x-Quadrat“ sondern die Kubikfunktion „x hoch drei“ an. Wir haben das gleiche Ausgangszenario: eine Sekante durch die Punkte P und Q. Wieder lassen wir Q auf dem Funktionsgraphen unendlich dicht an P annähern, wodurch die Differenz zwischen x und x-null unendlich klein wird. Diesmal fokussieren wir uns jedoch auf genau diese Differenz und nennen sie „h“. h ist also die Differenz von x und x-null. Aus „x“ wird dann „x-null plus h“. Dadurch können wir unsere Formel umschreiben. Im Nenner fällt nun „x-null“ raus, dadurch wird die Grenzwertbestimmung etwas einfacher. Da wir x unendlich dicht an x-null heranführen wollen, muss also deren Differenz „h“ gegen null gehen. Dann setzen wir im Zähler die entsprechenden Funktionsterme ein. Die kubische Klammer können wir anschließend auflösen, und sehen, dass „x-null hoch drei“ rausfällt. Wenn wir nun aus allen Summanden ein h rauskürzen, erkennen wir, dass, wenn h gegen null geht, diese zwei Summanden ebenfalls gegen null gehen. Übrig bleibt „drei x-null Quadrat“. Die kubische Funktion „x hoch drei“ hat also als Ableitung die Funktion „drei x Quadrat“. Damit können wir nun auch hier für jede Zahl die entsprechende Steigung an dieser Stelle berechnen. Ganz schön schlau und revolutionär, was sich diese beiden Genies Newton und Leibniz da überlegt haben. Wir fassen das Ganze noch einmal in einer Übersicht zusammen. Mithilfe der Grenzwertbestimmung können wir Ableitungsfunktionen rechnerisch ermitteln, mit denen wir dann die Steigung einer Funktion an jeder beliebigen Stelle berechnen können. Dabei berechnen wir den Differentialquotienten nicht für eine konkret festgelegte, sondern eine allgemeine Stelle „x-null“. Dafür gibt es zwei verschiedene Schreibweisen. Bei der x-Methode lassen wir x gegen „x-null“ laufen. Die h-Methode ist vor allem für komplexere Funktionen geeignet, da bei dieser Schreibweise nur das h im Nenner steht. Dadurch wird die Grenzwertbestimmung einfacher. Verschiedene Schreibweisen für die Ableitungsfunktion hatten übrigens auch Newton und Leibniz entwickelt. Ihr Prioritätsstreit über die Entdeckung der Differentialrechnung gehört zu den heftigsten und weitreichendsten Konflikten der Wissenschaftsgeschichte. Dabei hätten sie sich gar nicht so stark in die Haare kriegen müssen, weil mittlerweile anerkannt ist, dass sie unabhängig voneinander auf die Idee gekommen sind. Vielleicht hätten sie besser mal einen Gang runtergeschaltet und stattdessen zusammengearbeitet - dann hätten sie wohl noch viel mehr erreicht!
Ableitungsfunktion – Steigung einer Funktion an einer beliebigen Stelle Übung
-
Beschreibe die $x$-Methode zur Bestimmung der Ableitungsfunktion am Beispiel der Normalparabel.
Tipps$\lim\limits_{x \to x_0}$ nennen wir Grenzwert.
- binomische Formel: $(a+b)^2=a^2+2ab+b^2$
- binomische Formel: $(a-b)^2=a^2-2ab+b^2$
- binomische Formel: $(a+b)(a-b)=a^2-b^2$
LösungMithilfe des Grenzwertes der Sekantensteigung können wir die Steigung einer Funktion an einer bestimmten Stelle $x_0$ berechnen. Diesen Ausdruck nennen wir Differentialquotient:
$\lim\limits_{x \to x_0} \frac{f(x)-f(x_0)}{x-x_0}$Durch Einsetzen konkreter Werte und geschicktes Kürzen können wir diesen Grenzwert berechnen. Damit bestimmen wir die Steigung einer Tangenten an den Graphen von $f(x)$ and der Stelle $x_0$, was der Steigung des Graphen von $f(x)$ an dieser Stelle entspricht.
Wenn wir die Steigung in mehreren Punkten ermitteln wollen, dann ist es einfacher, den Differentialquotienten allgemein für eine beliebige Stelle $x_0$ zu bestimmen.
Für die Normalparabel $f(x)=x^2$ gehen wir dabei wie folgt vor:
$1.$ Wir setzen $f(x)$ in den Differentialquotienten ein:
$\lim\limits_{x \to x_0} \frac{f(x)-f(x_0)}{x-x_0} = \lim\limits_{x \to x_0} \frac{x^2-x_0^2}{x-x_0}$$2.$ Wir wenden die $3$. binomische Formel an und kürzen anschließend den Bruch:
$\lim\limits_{x \to x_0} \frac{x^2-x_0^2}{x-x_0} = \lim\limits_{x \to x_0} \frac{(x+x_0)(x-x_0}{x-x_0} = \lim\limits_{x \to x_0} (x+x_0)$$3.$ Wir bestimmen den Grenzwert:
$\lim\limits_{x \to x_0} (x+x_0) = 2x_0$Somit ergibt sich die Ableitung der Normalparabel $f'(x)=2x$. Mit ihr können wir die Steigung der Normalparabel an jeder beliebigen Stelle bestimmen.
-
Bestimme die Ableitung der gegebenen Funktion mithilfe der $h$-Methode.
TippsDefiniere zunächst die Variable $h$.
Der letzte Schritt ist das Formulieren der Ableitung.
LösungUm die Steigung in einem bestimmten Punkt zu bestimmen, betrachten wir zunächst eine Sekante durch zwei Punkte. Wir lassen dann den Punkt an der Stelle $x$ immer weiter auf den Punkt an der Stelle $x_0$ zuwandern, bis aus der Sekante eine Tangente wird. Durch diesen Grenzwertprozess können wir aus der Steigung im Intervall zwischen $x_0$ und $x$ die Steigung an der Stelle $x_0$ bestimmen.
Konkret gehen wir bei der $h$-Methode für die Funktion $f(x)=x^3$ dabei wie folgt vor:
$1.$ Definition von $h$:
Wir definieren den Abstand zwischen $x_0$ und $x$ als $h$: $x_0-x=h$$2.$ Differentialquotient aufstellen:
Wir schreiben den Differentialquotient als: $\quad \lim\limits_{h \to 0} \frac{f(x_0+h)-f(x_0)}{h}$$3.$ Einsetzen in den Differentialquotient:
Wir setzen die gegebene Funktion ein: $\quad \lim\limits_{h \to 0} \frac{(x_0+h)^3-x_0^3}{h}$$4.$ Klammer auflösen:
Wir multiplizieren die Klammer aus: $\quad \lim\limits_{h \to 0} \frac{x_0^3+3x_0^2 \cdot h + 3x_0 \cdot h^2+ h^3 - x_0^3}{h}$$5.$ Zusammenfassen:
Wir fassen die beiden $x_0^3$ zusammen: $\quad \lim\limits_{h \to 0} \frac{3x_0^2 \cdot h + 3x_0 \cdot h^2+ h^3}{h}$$6.$ Ausklammern:
Wir klammern $h$ im Nenner aus: $\quad \lim\limits_{h \to 0} \frac{h \cdot (3x_0^2 + 3x_0 \cdot h+ h^2)}{h}$$7.$ Kürzen:
Wir kürzen mit $h$: $\quad \lim\limits_{h \to 0} (3x_0^2 + 3x_0 \cdot h+ h^2)$$8.$ Grenzwert anwenden:
Wir lassen $h$ gegen $0$ gehen: $\quad \lim\limits_{h \to 0} (3x_0^2 + \underbrace{3x_0 \cdot h}_{\to 0}+ \underbrace{h^2}_{\to 0}) = 3x_0^2$$9.$ Formulieren der Ableitung:
Wir können nun die Ableitung angeben: $\quad f'(x)=3x^2$ -
Bestimme den Differentialquotienten.
TippsVereinfache zunächst den Bruch. Versuche ihn geschickt zu kürzen oder zu erweitern.
Du kannst die dritte binomische Formel anwenden:
$(a+b)(a-b)=a^2-b^2$
Beispiel: $f(x)=3\sqrt{x}+1 = 3x^\frac{1}{2}+1$
$\lim\limits_{x \to x_0} \frac{3x^\frac{1}{2}+1-3x_0^\frac{1}{2}-1}{x-x_0} =\lim\limits_{x \to x_0} \frac{3\bigl(x^\frac{1}{2}-x_0^\frac{1}{2}\bigr)}{x-x_0} = \lim\limits_{x \to x_0} \frac{3\bigl(x^\frac{1}{2}-x_0^\frac{1}{2}\bigr)\bigl(x^\frac{1}{2}+x_0^\frac{1}{2}\bigr)}{(x-x_0)\bigl(x^\frac{1}{2}+x_0^\frac{1}{2}\bigr)} =\lim\limits_{x \to x_0} \frac{3(x-x_0)}{(x-x_0)\bigl(x^\frac{1}{2}+x_0^\frac{1}{2}\bigr)} =\lim\limits_{x \to x_0} \frac{3}{x^\frac{1}{2}+x_0^\frac{1}{2}} = \frac{3}{x_0^\frac{1}{2}+x_0^\frac{1}{2}} = \frac{3}{2x_0^\frac{1}{2}} = \frac{3}{2}x_0^{-\frac{1}{2}}$LösungMithilfe des Differentialquotienten $\lim\limits_{x \to x_0} \frac{f(x)-f(x_0)}{x-x_0}$ können wir die Steigung einer Funktion an jeder beliebigen Stelle $x_0$ bestimmen.
Dazu formen wir den Differentialquotienten geschickt um, um dann den Grenzwert zu berechnen.
Im Folgenden ist jeweils auch die zugehörige Funktion angegeben, welche sich aus dem Zähler des Differentialquotienten ergibt.
Funktion 1: $f(x)=3x$
$\lim\limits_{x \to x_0} \frac{3x-3x_0}{x-x_0} = \lim\limits_{x \to x_0} \frac{3(x-x_0)}{x-x_0} = \lim\limits_{x \to x_0} 3 = 3 $Funktion 2: $f(x)=x^2+4$
$\lim\limits_{x \to x_0} \frac{x^2+4-x_0^2-4}{x-x_0} =\lim\limits_{x \to x_0} \frac{x^2-x_0^2}{x-x_0} =\lim\limits_{x \to x_0} \frac{(x+x_0)(x-x_0)}{x-x_0} =\lim\limits_{x \to x_0} x+x_0 = 2x_0 $Funkion 3: $f(x)=-\frac{1}{2}x^2$
$\lim\limits_{x \to x_0} \frac{-\frac{1}{2}x^2+\frac{1}{2}x_0^2}{x-x_0} = \lim\limits_{x \to x_0} \frac{-\frac{1}{2}(x^2-x_0^2)}{x-x_0} = \lim\limits_{x \to x_0} \frac{-\frac{1}{2}(x+x_0)(x-x_0)}{x-x_0} = \lim\limits_{x \to x_0} -\frac{1}{2}(x+x_0) = -\frac{1}{2} \cdot 2x_0 = -x_0$Funktion 4: $f(x)=\sqrt{x} = x^\frac{1}{2}$
$\lim\limits_{x \to x_0} \frac{x^\frac{1}{2}-x_0^\frac{1}{2}}{x-x_0} = \lim\limits_{x \to x_0} \frac{\bigl(x^\frac{1}{2}-x_0^\frac{1}{2}\bigr)\bigl(x^\frac{1}{2}+x_0^\frac{1}{2}\bigr)}{(x-x_0)\bigl(x^\frac{1}{2}+x_0^\frac{1}{2}\bigr)} =\lim\limits_{x \to x_0} \frac{x-x_0}{(x-x_0)\bigl(x^\frac{1}{2}+x_0^\frac{1}{2}\bigr)} =\lim\limits_{x \to x_0} \frac{1}{x^\frac{1}{2}+x_0^\frac{1}{2}} = \frac{1}{x_0^\frac{1}{2}+x_0^\frac{1}{2}} = \frac{1}{2x_0^\frac{1}{2}} = \frac{1}{2}x_0^{-\frac{1}{2}}$ -
Leite die Ableitung der gegebenen Funktion mit der $h$-Methode her und berechne die Ableitung an der Stelle $x_0=-2$.
TippsDurch Anwenden der $1.$ binomischen Formel kannst du die Klammer mit dem Quadrat auflösen.
Achte beim Kürzen darauf, dass du in allen Summanden kürzt.
$f'(x)=4x-1$
LösungWir betrachten die gegebene Funktion: $f(x)=2x^2-x$.
Beim Herleiten der Ableitung mithilfe der $h$-Methode setzen wir zunächst die Funktionsgleichung $f(x_0)$ und $f(x_0+h)$ in den Differentialquotienten ein. Dabei setzen wir im Zähler Klammen, um Vorzeichenfehler zu vermeiden.
$\begin{array}{ll} & \lim\limits_{h \to 0} \frac{f(x_0+h)-f(x_0)}{h} \\ = & \lim\limits_{h \to 0} \frac{2(x_0+h)^2-(x_0+h)-(2x_0^2-x_0)}{h} \end{array}$
Anschließend lösen wir die Klammern auf. Durch Anwenden der $1.$ binomischen Formel können wir die Klammer mit dem Quadrat auflösen.
$\begin{array}{ll} & \lim\limits_{h \to 0} \frac{2(x_0+h)^2-(x_0+h)-(2x_0^2-x_0)}{h} \\ = & \lim\limits_{h \to 0} \frac{ 2x_0^2+4x_0h+2h^2-(x_0+h)-(2x_0^2-x_0)}{h} \\ = & \lim\limits_{h \to 0} \frac{ 2x_0^2+4x_0h+2h^2-x_0-h-2x_0^2+x_0}{h} \end{array}$
Wir fassen dann den Zähler soweit wie möglich zusammen.
$\begin{array}{ll} & \lim\limits_{h \to 0} \frac{ 2x_0^2+4x_0h+2h^2-x_0-h-2x_0^2+x_0}{h} \\ = & \lim\limits_{h \to 0} \frac{ 4x_0h+2h^2-h}{h} \end{array}$
Nun können wir mit $h$ kürzen und zuletzt den Grenzwert bilden.
$\begin{array}{ll} & \lim\limits_{h \to 0} \frac{ 4x_0h+2h^2-h}{h} \\ = & \lim\limits_{h \to 0} 4x_0+2h-1 \\ = & 4x_0-1 \end{array}$
Damit ist die Ableitung $f'(x) = 4x - 1$.
Wir können also die Ableitung an der Stelle $x_0=-2$ berechnen, indem wir einsetzen:
$f'(-2)=4 \cdot (-2)-1 = -8-1=-9$
-
Berechne mithilfe der Ableitung die Steigung der Funktion an den gegebenen Stellen.
Tipps$f'(x)$ ist die Ableitungsfunktion und gibt die Steigung der Funktion $f(x)$ an jeder beliebigen Stelle an.
Setze die gegebenen Werte für $x$ in $f'(x)$ ein und berechne.
Beispiel: $x_0 = 1 \quad f'(1)=6 \cdot 1 = 6$
LösungDie Ableitung $f'(x)$ einer Funktion gibt die Steigung der Funktion $f(x)$ an.
Durch Einsetzen konkreter $x$-Werte können wir die Steigung der Funktion $f(x)$ an diesen Stellen berechnen.Wir betrachten die Funktion $f(x)=3x^2$ und deren Ableitung $f'(x)=6x$:
- $x_0 = 4 \qquad f'(4)=6 \cdot 4 = 24$
- $x_0 = -1 \,\quad f'(-1)=6 \cdot (-1) = -6$
- $x_0 = 0 \qquad f'(0)=6 \cdot 0 = 0$
- $x_0 = -2 \,\quad f'(-2)=6 \cdot (-2) = -12$
-
Überprüfe die Aussagen zum Differentialquotienten.
TippsBeispiel: $f(x)=-\frac{1}{2}x^2$
$\lim\limits_{x \to x_0} \frac{-\frac{1}{2}x^2+\frac{1}{2}x_0^2}{x-x_0} = \lim\limits_{x \to x_0} \frac{-\frac{1}{2}(x^2-x_0^2)}{x-x_0} = \lim\limits_{x \to x_0} \frac{-\frac{1}{2}(x+x_0)(x-x_0)}{x-x_0} = \lim\limits_{x \to x_0} -\frac{1}{2}(x+x_0) = -\frac{1}{2} \cdot 2x_0 = -x_0$LösungMithilfe des Differentialquotienten können wir die Steigung einer Funktion an einer Stelle $x_0$ bestimmen. Dabei gibt es zwei verschiedene Schreibweisen:
Die $x$-Methode: $\lim\limits_{x \to x_0} \frac{f(x)-f(x_0)}{x-x_0}$
Die $h$-Methode: $\lim\limits_{h \to 0} \frac{f(x_0+h)-f(x_0)}{h}$Indem wir eine beliebige Stelle $x_0$ wählen, können wir den Differentialquotienten allgemein bestimmen.
Wir überprüfen die Aussagen dazu:
Aussage 1:
Um den Grenzwert des Differentialquotienten zu bilden, müssen wir immer vorher kürzen.
Diese Aussage ist korrekt. Denn um den Grenzwert bilden zu können, muss die Nennernullstelle verschwinden. Dies erreichen wir durch Kürzen.
$\lim\limits_{x \to x_0} \frac{x^\frac{1}{2}-x_0^\frac{1}{2}}{x-x_0} = \lim\limits_{x \to x_0} \frac{\bigl(x^\frac{1}{2}-x_0^\frac{1}{2}\bigr)\bigl(x^\frac{1}{2}+x_0^\frac{1}{2}\bigr)}{(x-x_0)\bigl(x^\frac{1}{2}+x_0^\frac{1}{2}\bigr)} =\lim\limits_{x \to x_0} \frac{x-x_0}{(x-x_0)\bigl(x^\frac{1}{2}+x_0^\frac{1}{2}\bigr)} =\lim\limits_{x \to x_0} \frac{1}{x^\frac{1}{2}+x_0^\frac{1}{2}} = \frac{1}{x_0^\frac{1}{2}+x_0^\frac{1}{2}} = \frac{1}{2x_0^\frac{1}{2}} = \frac{1}{2}x_0^{-\frac{1}{2}}$Aussage 2:
Um den Differentialquotienten zu bestimmen, müssen wir die $3$. binomische Formel anwenden.
Diese Aussage ist falsch. Ein Gegenbeispiel dazu lautet: $f(x)=3x$
$\lim\limits_{x \to x_0} \frac{3x-3x_0}{x-x_0} = \lim\limits_{x \to x_0} \frac{3(x-x_0)}{x-x_0} = \lim\limits_{x \to x_0} 3 = 3 $
Hier wurde keine binomische Formel angewendet.Aussage 3:
Wir können für jede Funktion sowohl die $h$-Methode als auch die $x$-Methode anwenden.
Diese Aussage ist korrekt. Die beiden Methoden sind nur unterschiedliche Schreibweisen für die gleiche Grenzwert-Überlegung. Die $h$-Methode eignet sich eher für komplexere Funktionen, da hierbei der Differentialquotient besser vereinfacht werden kann.Aussage 4:
Bei quadratischen Funktionen kommt bei der Bestimmung des Differentialquotienten mit der $h$-Methode immer eine binomische Formel vor.
Diese Aussage ist korrekt. Da bei quadratischen Funktionen immer die Summe $(x_0+h)$ quadriert wird, müssen wir die erste binomische Formel anwenden, um den Ausdruck zu vereinfachen. Wir betrachten dazu die Funktion: $f(x)=ax^2$
$\lim\limits_{h \to 0} \frac{f(x_0+h)-f(x_0)}{h} =\lim\limits_{h \to 0} \frac{a(x_0+h)^2-ax_0^2}{h} =\lim\limits_{h \to 0} \frac{ a(x_0^2+2x_0h+h^2)-ax_0}{h} =\lim\limits_{h \to 0} \frac{ ax_0^2+2ax_0h+ah^2-ax_0}{h} = \lim\limits_{h \to 0} \frac{ 2ax_0h+ah^2}{h}= \lim\limits_{h \to 0} 2ax_0+ah= 2ax_0 $Aussage 5:
Die $x$-Methode eignet sich nur für quadratische Funktionen.
Diese Aussage ist falsch. Ein Gegenbeispiel dazu lautet: $f(x)=\sqrt{x}= x^\frac{1}{2}$
$\lim\limits_{x \to x_0} \frac{x^\frac{1}{2}-x_0^\frac{1}{2}}{x-x_0} = \lim\limits_{x \to x_0} \frac{\bigl(x^\frac{1}{2}-x_0^\frac{1}{2}\bigr)\bigl(x^\frac{1}{2}+x_0^\frac{1}{2}\bigr)}{(x-x_0)\bigl(x^\frac{1}{2}+x_0^\frac{1}{2}\bigr)} =\lim\limits_{x \to x_0} \frac{x-x_0}{(x-x_0)\bigl(x^\frac{1}{2}+x_0^\frac{1}{2}\bigr)} =\lim\limits_{x \to x_0} \frac{1}{x^\frac{1}{2}+x_0^\frac{1}{2}} = \frac{1}{x_0^\frac{1}{2}+x_0^\frac{1}{2}} = \frac{1}{2x_0^\frac{1}{2}} = \frac{1}{2}x_0^{-\frac{1}{2}}$Aussage 6:
Bei der Funktion $f(x)=x^2+b$ muss bei der Bestimmung des Differentialquotienten immer mit $b$ gekürzt werden.
Diese Aussage ist falsch. Wir betrachten dazu den Differentialquotienten:
$\lim\limits_{x \to x_0} \frac{x^2+b-x_0^2-b}{x-x_0} =\lim\limits_{x \to x_0} \frac{x^2-x_0^2}{x-x_0} =\lim\limits_{x \to x_0} \frac{(x+x_0)(x-x_0)}{x-x_0} =\lim\limits_{x \to x_0} x+x_0 = 2x_0 $
Wir erkennen, dass der Parameter $b$ bereits im ersten Schritt wegfällt, da $+b-b=0$.
8.905
sofaheld-Level
6.601
vorgefertigte
Vokabeln
7.695
Lernvideos
37.343
Übungen
33.674
Arbeitsblätter
24h
Hilfe von Lehrkräften
Inhalte für alle Fächer und Klassenstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebeziehungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Quadrat
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Was Ist Eine Viertelstunde
- Prisma
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Satz Des Pythagoras
- Dreieck Grundschule
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Zahlen In Worten Schreiben
- Meter
- Orthogonalität
- Schriftlich Multiplizieren
- Brüche gleichnamig machen
- Brüche Multiplizieren
- Potenzgesetze
- Distributivgesetz
- Bruchgleichungen lösen – Übungen
- Flächeninhalt Dreieck
- Rationale Zahlen
- Volumen Berechnen
