Strecken teilen
Eine Strecke hat einen Anfangs- und einen Endpunkt und damit auch eine Länge. Diese kannst du aufteilen.
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Was sind Strecken?
- Strecken in gleiche Teile teilen
- Innere und äußere Teilung einer Strecke
- Strecken in Verhältnisse teilen – innere Teilung
- Strecken in Verhältnisse teilen – äußere Teilung
Was sind Strecken?
Eine Strecke ist die geradlinige Verbindung zwischen zwei Punkten. Eine Strecke hat also einen Anfangspunkt (hier zum Beispiel $A$) und einen Endpunkt ($B$). Eine Strecke wird mit den beiden Punkten und einem Strich darüber, also $\overline{AB}$ beschrieben.
Die Orientierung der Strecke kann auch anders herum sein. Dann ist $B$ der Anfangs- und $A$ der Endpunkt.

Du kannst die Länge einer Strecke messen. Hierfür verwendest du ein Lineal oder ein Geodreieck. Wenn du eine Strecke teilen sollst, teilst du also die Länge der Strecke. Wie das geht siehst du im Folgenden.
Strecken in gleiche Teile teilen
Zunächst schauen wir uns an, wie du Strecken in gleiche Teile teilen kannst. Du siehst hier, wie du eine Strecke in $4$ gleich große Teile teilen kannst. Du gehst wie folgt vor.
- Zeichne ausgehend von einem Endpunkt der Strecke (im folgenden Bild ist dies $A$) einen Hilfsstrahl. Dieser muss mit der Strecke einen spitzen Winkel einschließen.
- Schätze ungefähr ein Viertel der Länge der Strecke ab. Stelle einen Zirkel auf diese geschätzte Größe ein. Nun zeichnest du um $A$ einen Kreisbogen mit dem Zirkel. Dieser Kreisbogen schneidet den Hilfsstrahl.
- Zeichne um diesen Schnittpunkt wieder einen Kreisbogen mit dem gleichen Radius. Auch dieser schneidet den Hilfsstrahl.
- Fahre so fort, bis du $4$ gleich große Abschnitte auf dem Hilfsstrahl konstruiert hast.
- Verbinde nun den letzten Schnittpunkt auf dem Hilfsstrahl mit dem anderen Endpunkt der Strecke (im folgenden Bild ist dies $B$).
- Schließlich verschiebst du diese Verbindung parallel in jeden der drei weiteren Schnittpunkte auf dem Hilfsstrahl. Jede der parallel verschobenen Verbindungen schneidet die Strecke $\overline{AB}$.
- Die Schnittpunkte der Verbindungslinien mit der Strecke $\overline{AB}$ teilen diese in vier gleiche Teile. Du erhältst auf diese Weise also $4$ gleich große Abschnitte der Strecke $\overline{AB}$.
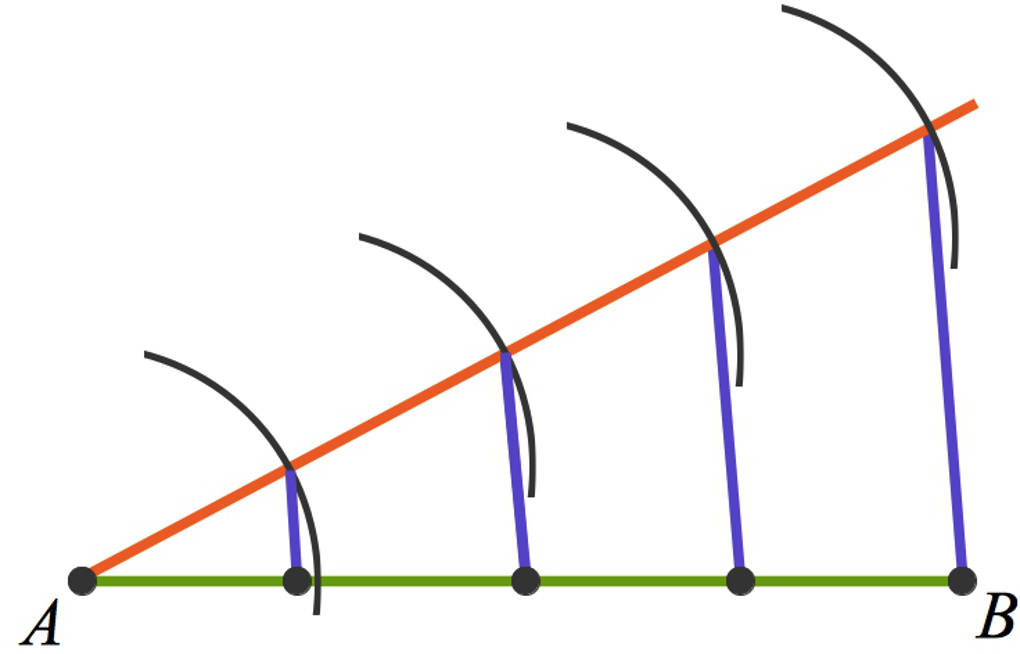
Warum sind diese Abschnitte tatsächlich gleich groß? Mit Hilfe des Strahlensatzes siehst du, dass zu gleich langen Abschnitten auf dem Strahl auch gleich lange Abschnitte auf der Strecke gehören müssen.
Innere und äußere Teilung einer Strecke
Du kannst Strecken auch in einem gegebenen Verhältnis teilen. Dabei wird die innere sowie die äußere Teilung unterschieden.
Strecken in Verhältnisse teilen – innere Teilung
Du sollst eine innere Teilung einer Strecke durchführen. Dabei ist das Teilungsverhältnis gegeben. Schauen wir uns die Strecke $\overline{AB}$ an. Diese Strecke soll im Verhältnis $3:2$ geteilt werden. Das bedeutet: Gesucht ist ein Punkt $P$ auf der Strecke $\overline{AB}$, welcher diese Strecke in dem gegebenen Verhältnis teilt.
- Zunächst überlegst du dir, wie viele gleich große Teile der Strecke du benötigst: Da das Verhältnis $3:2$ vorgegeben ist, benötigst du einmal $3$ Teilstrecken und einmal $2$. Das sind zusammen $3+2=5$ Teilstrecken.
- Nun teilst du, wie bereits beschrieben, die Strecke $\overline{AB}$ in $5$ gleich große Abschnitte.
- Damit der Punkt $P$ die Strecke $\overline{AB}$ im Verhältnis $3:2$ per innerer Teilung teilt, muss die Strecke $\overline{AP}$ drei und die Strecke $\overline{PB}$ zwei der gleich großen Teilstrecken umfassen.
Die beschriebenen Konstruktionsschritte kannst du folgendem Bild entnehmen.
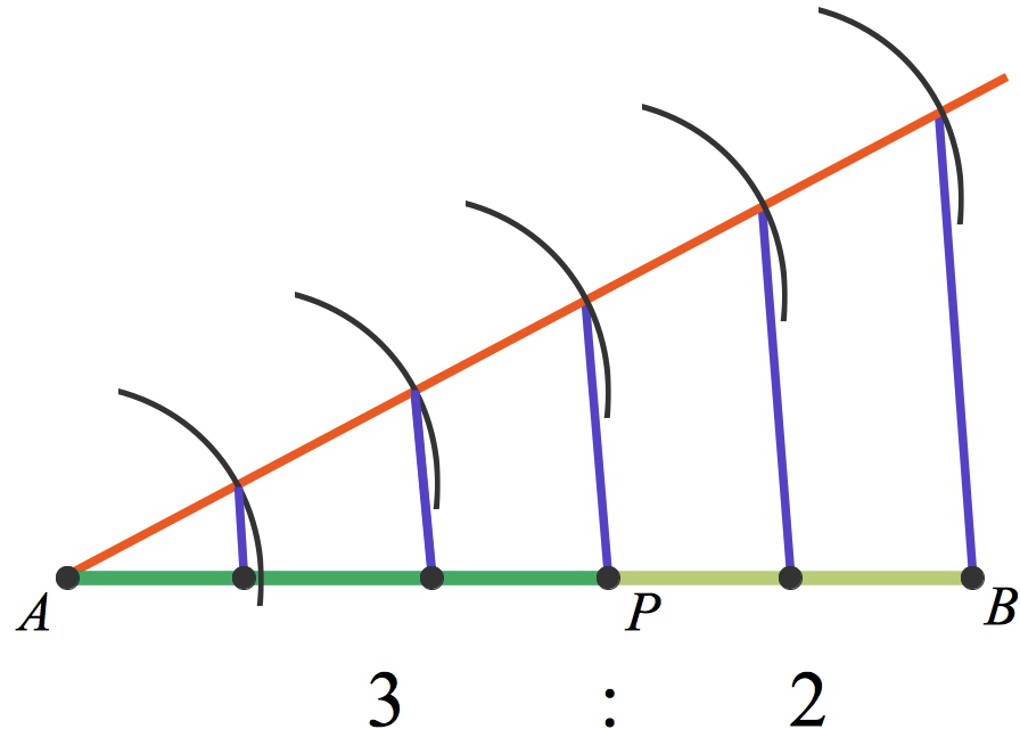
Strecken in Verhältnisse teilen – äußere Teilung
Ähnlich wie bei der inneren Teilung gehst du auch bei der äußeren Teilung vor: Dieses Mal soll der Punkt $P$ allerdings außerhalb der Strecke $\overline{AB}$ liegen, zum Beispiel auf der von $A$ aus gesehen anderen Seite von $B$. Trotzdem betrachten wir weiterhin das Verhältnis der Streckenlängen $\overline{AP}$ und $\overline{PB}$. Das Teilungsverhältnis ist dann negativ, da die beiden Strecken in die gegengesetzte Richtung verlaufen. Äußere Teilungsverhältnisse sind also immer negativ. Das Vorgehen bei der äußeren Teilung schauen wir uns wieder an dem Teilungsverhältnis $3:2$ bzw. in diesem Fall dann $-3:2$ an. Die Strecke $\overline{AP}$ entspricht dann $3$ und die Strecke $\overline{PB}$ $2$ gleich großen Teilstrecken.
Für die Konstruktion des Punktes $P$ der die Strecke $\overline{AB}$ im gegebenen Verhältnis teilt, gehst du wie folgt vor:
- Du zeichnest zwei parallele Hilfsstrecken durch $A$ und $B$ auf der gleichen Seite der Strecke $\overline{AB}$.
- Auf diesen trägst du gleichlange Teilstrecken ab: $3$ bei $A$ und $2$ bei $B$.
- Nun verbindest du die beiden äußeren Markierungen bei $A$ und $B$ zu einer Geraden.
- Der Schnittpunkt dieser Geraden mit der Verlängerung von $\overline{AB}$ ist der gesuchte Punkt $P$, der die Strecke $\overline{AB}$ im Verhältnis $-3:2$ teilt!
Alle Videos und Lerntexte zum Thema
Videos und Lerntexte zum Thema
Strecken teilen (2 Videos, 2 Lerntexte)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Strecken teilen (3 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung






 Strecken in gleiche Teile teilen
Strecken in gleiche Teile teilen
 Strecken in Verhältnisse teilen – innere Teilung
Strecken in Verhältnisse teilen – innere Teilung
 Goldener Schnitt
Goldener Schnitt









