Scharen von Exponentialfunktionen – Kurvendiskussion (2)


in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
Grundlagen zum Thema Scharen von Exponentialfunktionen – Kurvendiskussion (2)
Hallo, mein Name ist Frank. Kennst du dich aus mit Exponentialfunktionen? Weißt du, welche Punkte bei einer Kurvendiskussion zu beachten sind? Gut, dann kannst du dir ja jetzt mal eine Exponentialfunktion mit Parameter anschauen. Du wirst sehen, wie sich der Parameter auf den Verlauf der Funktion auswirkt. Solltest du Fragen haben, so schreibe gerne einen Kommentar und ich werde deine Frage dann beantworten.
Scharen von Exponentialfunktionen – Kurvendiskussion (2) Übung
-
Bestimme die Ableitungen sowie die Koordinatenschnittpunkte der Kurvenschar.
TippsWende zum Ableiten die Produktregel an:
$(uv)'=u'v+uv'$.
Für die Nullstellen löst du die Gleichung $f_a(x)=0$.
Beachte, dass $e^x\neq 0$ ist.
Für den y-Achsenabschnitt setzt du $x=0$ in der Funktionsgleichung ein.
LösungAbleitungen
Um eine Kurvendiskussion durchzuführen, benötigt man auf jeden Fall die ersten (drei!) Ableitungen. Da diese Funktion das Produkt zweier Funktionen ist, verwendet man die Produktregel:
$(uv)'=u'v+uv'$.
Damit ist
$f_a'(x)=e^x(1-ax)+e^x(-a)$.
Nun kann der gemeinsame Faktor $e^x$ ausgeklammert werden zu
$f_a'(x)=e^x(1-ax-a)=e^x(1-a-ax)$.
Ebenso können die zweite und dritte Ableitung bestimmt werden:
- $f_a''(x)=e^x(1-2a-ax)$
- $f_a'''(x)=e^x(1-3a-ax)$
Es muss die Gleichung $f_a(x)=0$ gelöst werden:
$e^x(1-ax)=0$.
Da $e^x\neq 0$ ist, muss $1-ax=0$ sein. Dies ist äquivalent zu
$x=\frac1a$.
Damit ist N$\left(\frac1a\big\vert0\right)$ die gesuchte Nullstelle.
Y-Achsenabschnitt
Hierfür wird $x=0$ in der Funktionsgleichung eingesetzt:
$f_a(0)=e^0(1-a\cdot 0)=1$.
Der y-Achsenabschnitt ist $Y(0|1)$.
-
Ermittle die Extrema sowie deren Ortskurve.
TippsDie ersten beiden Ableitungen sind
- $f_a'(x)=e^x(1-a-ax)$ sowie
- $f_a''(x)=e^x(1-2a-ax)$.
Es muss gelten $f_a'(x)=0$.
Wenn du diese Gleichung löst, erhältst du ein $x_E$.
Zusätzlich muss $f_a''(x_E) \neq 0$ gelten.
Sowohl die x- als auch die y-Koordinate des Extremums hängen von dem Parameter $a$ ab.
Forme die x-Koordinate nach $a$ um und setze dieses $a$ in der y-Koordinate ein.
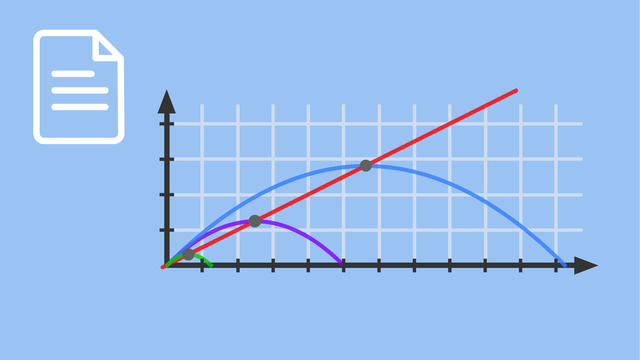
LösungHier sind drei Kurven der Schar zu sehen sowie die Ortskurve der Extrema (grau).
Wie kann diese Ortskurve bestimmt werden?
Zunächst muss die Kurvenschar auf Extrema untersucht werden.
Die ersten beiden Ableitungen der Funktion $f_a(x)=e^x(1-ax)$ sind
- $f_a'(x)=e^x(1-a-ax)$ sowie
- $f_a''(x)=e^x(1-2a-ax)$.
$\begin{array}{rcl} 1-a-ax&=&0&|&+ax\\ 1-a&=&ax&|&:a\\ \frac1a-1&=&x \end{array}$
Nun muss diese Lösung noch in der zweiten Ableitung eingesetzt werden. Diese muss hinreichend ungleich $0$ sein:
$\begin{array}{rcl} f_a''\left(\frac1a-1\right)&=&e^{\frac1a-1}\left(1-2a-a\left(\frac1a-1\right)\right)\\ &=&e^{\frac1a-1}(1-2a-1+a)\\ &=&-ae^{\frac1a-1}<0 \end{array}$
Das bedeutet, dass die Funktion einen Hochpunkt besitzt. Für die y-Koordinate setzt man $x=\frac1a-1$ in der Funktionsgleichung ein:
$f_a\left(\frac1a-1\right)=e^{\frac1a-1}\left(1-a\left(\frac1a-1\right)\right)=a\cdot e^{\frac1a-1}$.
$HP\left(\frac1a-1\big\vert a\cdot e^{\frac1a-1}\right)$.
Ortskurve
Zunächst wird $x=\frac1a-1$ nach $a$ umgeformt.
- Addition von $1$ führt zu $x+1=\frac1a$.
- Nun wird der Kehrwert gebildet: $a=\frac1{x+1}$.
$y=\frac1{x+1}\cdot e^{x+1-1}=\frac1{x+1}\cdot e^x$.
Dies ist die gesuchte Ortskurve
$y(x)=\frac1{x+1}\cdot e^x$.
-
Gib die Koordinatenschnittpunkte der Funktion an und untersuche das Grenzwertverhalten.
TippsDu kannst einige der Aussagen bereits mit dem oben zu sehenden Graphen untersuchen.
Beachte: Es sind die Nullstellen sowie der y-Achsenabschnitt der Kurvenschar gemeint. Beide hängen von dem Parameter $a$ ab.
Es gilt
- $\lim\limits_{x\to \infty}e^{-x}=0$ und
- $\lim\limits_{x\to -\infty}e^{-x}=„\infty“$.
LösungDie Nullstellen sind die Lösungen der Gleichung $f_a(x)=0$.
$\begin{array}{crclll} &(ax+1)\cdot e^{-x+a}&=&0&|&e^{-x+a}\neq 0\\ \Leftrightarrow&ax+1&=&0&|&-1\\ &ax&=&-1&|&:a\\ &x&=&-\frac1a \end{array}$
Also hängen die Nullstellen bereits von dem Parameter $a$ ab. Für $a=1$ ist $x=-1$ die Nullstelle (siehe Funktionsgraph).
Für den y-Achsenabschnitt setzt man $x=0$ in der Funktionsgleichung ein:
$y=f_a(0)=(a\cdot 0+1)\cdot e^{-0+a}=e^a$.
Für $a=1$ erhält man $y=e$.
Grenzwerte
Wenn $x$ sehr groß wird, wird $ax+1$ ebenfalls sehr groß, $e^{-x+a}$ geht jedoch viel schneller gegen $0$. Deshalb ist
$\lim\limits_{x\to \infty}f(x)=0$.
Nun kann $x\to -\infty$ betrachtet werden: $ax+1$ geht ebenfalls gegen $-\infty$ und $e^{-x+a}$ gegen $\infty$. Damit gilt gesamt
$\lim\limits_{x\to -\infty}f(x)=„-\infty“$.
Die Grenzwerte kann man an dem Graphen bereits erkennen.
-
Untersuche die Funktionenschar auf Extrema.
TippsVerwende für die Ableitungen die Produktregel: $(uv)'=u'v+uv'$.
Die erste Ableitung muss $0$ sein. Dies führt zu einer Gleichung.
Deren Lösung(en) setzt du in der zweiten Ableitung ein: Ist diese
- positiv, dann liegt ein Tiefpunkt vor, oder
- negativ, dann liegt ein Hochpunkt vor.
Sowohl die x- als auch die y-Koordinate des Extremums hängt von dem Parameter $a$ ab.
LösungUm diese Funktion auf Extrema zu untersuchen, benötigt man die ersten beiden Ableitungen. Hierfür verwendet man die Produktregel $(uv)'=u'v+uv'$:
$\begin{array}{crlll} f'(x)&=&a\cdot e^{-x+a}-(ax+1)e^{-x+a}&|&\text{ Ausklammern}\\ &=&(-ax+a-1)e^{-x+a} \end{array}$
und die zweite Ableitung
$\begin{array}{crlll} f''(x)&=&-a\cdot e^{-x+a}-(-ax+a-1)e^{-x+a}&|&\text{ Ausklammern}\\ &=&(ax-2a+1)e^{-x+a} \end{array}$
Für Extrema muss notwendigerweise gelten, dass die erste Ableitung $0$ ist:
$\begin{array}{crclll} &(-ax+a-1)e^{-x+a}&=&0&|&e^{-x+a}\neq 0\\ \Leftrightarrow&-ax+a-1&=&0&|&-a+1\\ &-ax&=&-a+1&|&:(-a)\\ &x&=&1-\frac1a \end{array}$
Nun muss der gefundene Wert hinreichend in der zweiten Ableitung eingesetzt werden, um zum einen herauszufinden, ob und falls ja, welches Extremum vorliegt.
$f_a''\left(1-\frac1a\right)=\left(a\cdot\left(1-\frac1a\right)-2a+1\right)e^{-\left(1-\frac1a\right)+a}=-ae^{-\left(1-\frac1a\right)+a}<0$
Da $e^{~~}$ immer positiv ist und $-a$ negativ, liegt ein Hochpunkt vor.
Nun muss noch die y-Koordinate des Extremums berechnet werden:
$y=f_a\left(1-\frac1a\right)=\left(a\cdot\left(1-\frac1a\right)+1\right)e^{-\left(1-\frac1a\right)+a}=ae^{-1+\frac1a+a}$.
Somit lautet der Hochpunkt
$HP\left(1-\frac1a\big\vert a e^{-1+\frac1a+a}\right)$.
-
Beschreibe die Herleitung und die Bedeutung der Ortskurve der Extrema.
TippsSchaue dir das folgende Beispiel an: $E\left(a\big\vert\frac1a\right)$.
Hier ist
- $x(a)=a$ und
- $y(a)=\frac1a$.
Somit ist also $a=x$.
Setze dieses $a$ in der y-Koordinate ein:
$y=y(x)=\frac1x$.
Dies ist die gesuchte Ortskurve.
LösungWenn man alle Extrema einer Kurvenschar in ein Koordinatensystem einträgt, erhält man wieder eine Kurve.
Diese Kurve, auf der alle Extrema liegen, wird als Ortskurve der Extrema bezeichnet.
Wie kann diese Ortskurve bestimmt werden?
- Zuerst formt man die x-Koordinate, welche von dem Parameter $a$ abhängen muss, nach diesem Parameter um. Der Parameter ist nun in Abhängigkeit von $x$ gegeben.
- Nun wird der Parameter in der y-Koordinate eingesetzt. Diese hängt nun von $x$ ab.
-
Bestimme die Ortskurve der Extrema und ordne den Graphen den zugehörigen Parameter zu.
TippsForme die x-Koordinate des Hochpunktes nach $a$ um und setze dieses $a$ in der y-Koordinate ein: So erhältst du die Ortskurve der Extrema.
Es ist
$a=\frac1{1-x}$.
Um den jeweiligen Graphen zu identifizieren, kannst du für $a$ verschiedene Werte in dem Hochpunkt einsetzen.
Übrigens:
- Die Nullstelle der Funktionenschar ist $x=-\frac1a$ und
- die Funktionenschar schneidet die y-Achse bei $e^a$.
LösungDer Hochpunkt dieser Funktion lautet
$HP\left(1-\frac1a\big\vert ae^{-1+\frac1a+a}\right)$.
Ortskurve
Zuerst wird die x-Koordinate nach $a$ umgeformt:
$\begin{array}{rclll} x&=&1-\frac1a&|&-1\\ x-1&=&-\frac1a&|&:(-1)\\ 1-x&=&\frac1a&|&\text{ Kehrwert}\\ \frac1{1-x}&=&a \end{array}$
Dieses $a$ wird in der y-Koordinate eingesetzt:
$y=\frac1{1-x}e^{-1+\frac1{\frac1{1-x}}+\frac1{1-x}}=\frac1{1-x}e^{-x+\frac1{1-x}}$.
Die gesuchte Ortskurve ist somit
$y(x)=\frac1{1-x}e^{-x+\frac1{1-x}}$.
Um nun herauszufinden, welcher Wert für den Parameter $a$ zu welchem Graphen gehört, kann man sich den entsprechenden Hochpunkt anschauen. Dabei genügt eigentlich schon die x-Koordinate:
- Bei dem roten Graphen ist $x=0$, also ist $a=\frac1{1-0}=1$.
- Bei dem grünen Graphen ist $x=-1$, also ist $a=\frac1{1-(-1)}=\frac12=0,5$.
- Bei dem blauen Graphen ist die x-Koordinate nicht so exakt abzulesen. Diese ist $x=\frac13$, also ist $a=\frac1{1-\frac13}=\frac32=1,5$.

Ortskurve (Ortslinie) bei Parabelscharen – Beispiele
Ortskurve (Ortslinie) bei ganzrationalen Funktionen

Parabelscharen

Parabelscharen – Beispiele

Scharen von Wurzelfunktionen – Kurvendiskussion

Scharen von Exponentialfunktionen – Kurvendiskussion (1)

Scharen von Exponentialfunktionen – Kurvendiskussion (2)

Scharen von Logarithmusfunktionen – Kurvendiskussion

Schar von Winkelfunktionen – Kurvendiskussion
9.892
sofaheld-Level
6.600
vorgefertigte
Vokabeln
8.306
Lernvideos
38.669
Übungen
33.706
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Klassenstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung




 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?









Hallo Merry.
Die Ableitung von e^x ist e^x selbst.
Die verwendete Ableitungsregel ist die Produktregel: (uv)'=u'v+uv'
Hoffe, Du kommst damit weiter.
Hallo Frank,
bei 2:28, wo du die erste Ableitung bildest (genau unter der Überschrift), muss da nicht e hoch x * (-1) stehen, da a wie eine Konstante behandelt wird und nur -x abgeleitet werden muss?
Hallo Regina:
Da e^x nie 0 werden kann, genügt es den linearen Term zu betrachten. Dieser muss 0 sein: 1-ax=0 <=> x=1/a.
warum wird nicht erklärt wie man auf die nullstellen kommt. das sind vllt 2 zeilen die man mehr schreiben müsste verstehe ich nicht....
Vielen Dank. Ist mir dann auch im Nachhinein aufgefallen.