Ortskurve (Ortslinie) bei ganzrationalen Funktionen
Die Ortskurve verläuft durch die Extrem- und Wendepunkte einer Kurvenschar. Entdecke, wie du diese Kurve bestimmst und was sie dir über die Graphenfamilie verrät. Neugierig? Lies weiter!
- Was ist eine Kurvenschar?
- Was ist eine Ortskurve (Ortslinie)?
- Wie bestimmt man die Ortskurve?
- Beispiel 1: Ortskurve der Hochpunkte der Flugparabel
- Schritt 1: Hochpunkt in Abhängigkeit des Parameters bestimmen
- Schritt 2: Ortskurve der Hochpunkte bestimmen
in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
Lerntext zum Thema Ortskurve (Ortslinie) bei ganzrationalen Funktionen
Was ist eine Kurvenschar?
Wenn du einer Funktionsgleichung begegnest, die zwei Variablen enthält, handelt es sich wahrscheinlich um eine Funktion mit Parameter, auch Scharfunktion oder Funktionsschar genannt. Ein Beispiel ist $f_{v}(x)=-\frac{1}{v^2}x^2+0{,}1x$.
Hier ist $x$ die Funktionsvariable und $v$ der Parameter.
Es handelt sich um die Modellierung der Flugbahn eines Fußballs bei verschiedenen Schussgeschwindigkeiten $v$. Die Flughöhe $f(x)$ wird jeweils in Abhängigkeit von der Flugweite $x$ angegeben. Wenn man einen festen Wert für $v$ in die Funktionsgleichung einsetzt, erhält man einen Funktionsterm und einen Graphen.
Für $v=10$ gilt ${f_{10}(x)=-\frac{1}{100}x^2+0{,}1x}$.
Betrachtet man alle Funktionsterme $f_v(x)$ gemeinsam, erhält man eine Familie von Graphen, die sogenannte Kurvenschar.
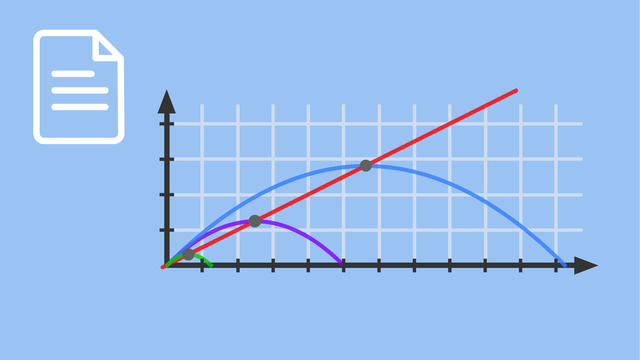
In der Abbildung siehst du drei Graphen ($f_5(x), f_{10}(x)$ und $f_{15}(x)$) der unendlich viele Graphen umfassenden Kurvenschar.
Alle Graphen einer Kurvenschar haben Gemeinsamkeiten und Unterschiede. In diesem Beispiel kannst du sehen, dass alle Graphen nach unten geöffnet sind und eine Nullstelle im Ursprung haben (die Anstoßstelle des Fußballs). Als Unterschied ist zu benennen, dass die Parabeln verschiedene Streckfaktoren und unterschiedliche Koordinaten der Extrempunkte und zweiten Nullstelle haben (da sich die Flughöhe und Flugweite des Fußballs mit der Schussgeschwindigkeit $v$ ändern). Kurvenscharen gibt es für alle Funktionsklassen. In diesem Text werden wir Beispiele für ganzrationale Funktionen betrachten.
Eine Kurvenschar (Funktionenschar) ist eine Menge verschiedener Kurven (Funktionsgraphen), die entstehen, wenn man verschiedene Werte für den Parameter in einer Scharfunktion einsetzt.
Was ist eine Ortskurve (Ortslinie)?
Betrachte erneut die Flugbahnen für den Fußball bei verschiedenen Schussgeschwindigkeiten.
Anhand der Kurvenschar ist zu sehen, dass die Extrempunkte wiederum auf einer Kurve (in diesem Fall auf einer Geraden) liegen. Das ist die sogenannte Ortskurve (auch: Ortslinie). Den Funktionsterm der Ortskurve (bzw. Ortslinie) kann man rechnerisch bestimmen. Dazu werden zunächst die charakteristischen Punkte mit den Methoden der Kurvendiskussion bestimmt. Beim Lösen von Gleichungen, Ableiten und Integrieren wird der Parameter wie eine Zahl behandelt. Die Nullstellen, Extrempunkte oder Wendepunkte werden in Abhängigkeit vom Parameter berechnet und angegeben.
Eine Ortskurve ist eine Kurve, die durch gewisse charakteristische Punkte (wie Extrempunkte oder Wendepunkte) der Graphen einer Kurvenschar verläuft. Mithilfe einer Ortskurve kann man eine Funktionsschar genauer beschreiben.
Die Begriffe Ortskurve und Ortslinie werden oft synonym verwendet.
Der Begriff Ortskurve wird vor allem im Kontext von Funktionsgraphen im zweidimensionalen, kartesischen Koordinatensystem verwendet.
Der Begriff Ortslinie wird auch im Zusammenhang mit geometrischen Konstruktionen verwendet, zum Beispiel zur Beschreibung von Kreisen.
Wie bestimmt man die Ortskurve?
Man kann die Ortskurve der Extrempunkte oder der Wendepunkte bestimmen. Das Vorgehen ist in beiden Fällen gleich und umfasst zwei Schritte.
Vorgehen zur Bestimmung einer Ortskurve:
- Bestimme den charakteristischen Punkt in Abhängigkeit vom Parameter.
- Stelle die beiden Gleichungen für die $x$- und $y$-Koordinate des Punkts auf, setze die Gleichungen ineinander ein und isoliere $y$. Die so erhaltene Gleichung ist die Funktionsgleichung der Ortskurve.
Beispiel 1: Ortskurve der Hochpunkte der Flugparabel
Wir bestimmen die Ortskurve der Hochpunkte für das obige Beispiel der Flugbahnen des Fußballs.
Schritt 1: Hochpunkt in Abhängigkeit des Parameters bestimmen
Bilde zunächst die ersten beiden Ableitungen. Der Parameter $v$ wird wie eine Zahl behandelt, wir leiten nach $x$ ab.
$f_v(x)=-\dfrac{1}{v^2}x^2+0{,}1x$
$f^{\prime}_v(x)=-\dfrac{2}{v^2}x+0{,}1$
$f^{\prime\prime}_v(x)=-\dfrac{2}{v^2}$
Setze die erste Ableitung gleich null und setze die Lösung in die zweite Ableitung ein.
$f^{\prime}_v(x)=0 \Longrightarrow -\dfrac{2}{v^2}x+0{,}1=0 \Longrightarrow -\dfrac{2}{v^2}x=-0{,}1 \Longrightarrow x=0{,}05v^2$
$f^{\prime\prime}_v(0{,}05v^2)=-\dfrac{2}{v^2}$
Weil wir für $v$ sinnvollerweise nur positive Werte einsetzen können ($v$ beschreibt die Schussgeschwindigkeit) und $v$ in der Funktionsgleichung der zweiten Ableitung quadriert wird, ist die zweite Ableitung insgesamt für jedes $v$ negativ.
Es gilt $f^{\prime}_v(0{,}05v^2)=0$ und $f^{\prime\prime}_v(0{,}05v^2)<0$, damit liegt bei $x=0{,}05 v^2$ ein Hochpunkt.
Berechnung der $y$-Koordinate:
$f_v(0{,}05v^2)=-\dfrac{1}{v^2}(0{,}05v^2)^2+0{,}1\cdot 0{,}05 v^2 = -\dfrac{1}{v^2}(0{,}0025 v^4)+ 0{,}005 v^2$
$= -(0{,}0025 v^2)+ 0{,}005 v^2=0{,}0025 v^2$
Der Hochpunkt liegt bei $H(0{,}05v^2\,\vert\,0{,}0025 v^2)$.
Schritt 2: Ortskurve der Hochpunkte bestimmen
Da wir den Hochpunkt einer Parameterfunktion bestimmt haben und mindestens eine Koordinate vom Parameter $v$ abhängt, handelt es sich bei $H(0{,}05v^2\,\vert\,0{,}0025 v^2)$ um unendlich viele Punkte. Diese Punkte liegen alle auf einer Kurve, für die beide Koordinaten erfüllt sind. Das heißt, dass beide Gleichungen $x=0{,}05v^2$ und $y=0{,}0025 v^2$ gelten. Wir formen die erste Gleichung nach $v^2$ um, sodass wir sie in die zweite Gleichung einsetzen können.
$v^2=\dfrac{x}{0{,}05}$ in $y=0{,}0025 v^2$ eingesetzt ergibt
$y=0{,}0025\cdot \dfrac{x}{0{,}05}=0{,}05x$.
Die Ortskurve der Hochpunkte ist in diesem Fall durch die Funktionsgleichung $y=0{,}05x$ gegeben. Vergleiche mit der Abbildung oben (rote Gerade).
Beispiel 2: Ortskurve der Tiefpunkte einer Funktion dritten Grads
Bestimme die Ortskurve der Tiefpunkte von $f_{b}(x)=0{,}1x^3-1{,}2b^2x \text{ mit } b>0$.
Schritt 1: Tiefpunkt in Abhängigkeit des Parameters bestimmen
Ableitungen:
$f_{b}(x)=0{,}1x^3-1{,}2b^2x$
$f^{\prime}_b(x)=0{,}3x^2-1{,}2b^2$
$f^{\prime\prime}_b(x)=0{,}6x$
Nullstellen der ersten Ableitung:
$f^{\prime}_b(x)=0 \Longrightarrow 0{,}3x^2-1{,}2b^2=0 \Longrightarrow 0{,}3x^2=1{,}2b^2 \Longrightarrow x^2=4 b^2$
$x_{1{,}2}=\pm 2b$
Einsetzen in die zweite Ableitung:
$f^{\prime\prime}_b(+2b)=0{,}6\cdot 2b=1{,}2b$
$\text{wegen } b>0 \text { gilt } f^{\prime\prime}_b(+2b)>0 \Longrightarrow \text { Tiefpunkt bei } x=1{,}2b$
$f^{\prime\prime}_b(-2b)=0{,}6\cdot (-2b)=-1{,}2b$
$\text{wegen } b>0 \text { gilt } f^{\prime\prime}_b(-2b)<0 \Longrightarrow \text { Hochpunkt bei } x=-1{,}2b$
Berechnung der $y$-Koordinate des Tiefpunkts:
$f_{b}(2b)=0{,}1\cdot (2b)^3-1{,}2b^2\cdot 2b =0{,}8 b^3-2{,}4 b^3= -1{,}6 b^3$
Der Tiefpunkt liegt bei $T(2b\,\vert-1{,}6 b^3)$.
Schritt 2: Ortskurve der Tiefpunkte bestimmen
Die Ortskurve muss die beiden Gleichungen $x=2b$ und $y=-1{,}6 b^3$ erfüllen.
Forme die erste Gleichung nach $b$ um und setze $b=\frac{x}{2}$ in die zweite Gleichung ein:
$y=-1{,}6\left(\dfrac{x}{2}\right )^3=-0{,}2 x^3$
Die Ortskurve der Tiefpunkte entspricht dem Graphen von $y=-0{,}2 x^3$. Vergleiche mit der folgenden Abbildung (roter Graph).
Beispiel 3: Ortskurve der Wendepunkte
Bestimme die Ortskurve der Wendepunkte von $f_{t}(x)=\frac{1}{6}x^3-4tx^2$.
Schritt 1: Wendepunkt in Abhängigkeit des Parameters bestimmen
Ableitungen:
$f_{t}(x)=\dfrac{1}{6}x^3-4tx^2$
$f^{\prime}_{t}(x)=\dfrac{1}{2}x^2-8tx$
$f^{\prime\prime}_{t}(x)=x-8t$
$f^{\prime\prime\prime}_{t}(x)=1$
Nullstellen der zweiten Ableitung:
$f^{\prime\prime}_{t}(x)=0 \Longrightarrow x-8t=0 \Longrightarrow x=8t$
Es gilt $f^{\prime\prime}_{t}(8t)=0$ und $f^{\prime\prime\prime}_{t}(8t)\neq 0$, also liegt bei $x=8t$ eine Wendestelle vor.
Berechnung der $y$-Koordinate:
$f_{t}(8t)=\frac{1}{6} (8t)^3-4t(8t)^2=\frac{1}{6}\cdot 512 t^3-4t \cdot 64t^2=\frac{256}{3}t^3-256 t^3=-\frac{512}{3}t^3$
Der Wendepunkt liegt bei $WP(8t\,\vert-\frac{512}{3}t^3)$.
Schritt 2: Ortskurve der Wendepunkte bestimmen
Die Ortskurve muss die beiden Gleichungen $x=8t$ und $y=-\frac{512}{3}t^3$ erfüllen.
Forme die erste Gleichung nach $t$ um und setze $t=\frac{x}{8}$ in die zweite Gleichung ein:
$y=-\dfrac{512}{3}\left( \dfrac{x}{8}\right)^3=-\dfrac{512}{3}\left( \dfrac{x^3}{512}\right)=-\dfrac{1}{3}x^3$
Die Ortskurve der Wendepunkte entspricht dem Graphen von $y=-\dfrac{1}{3}x^3$.
Ortskurve (Ortslinie) bei ganzrationalen Funktionen Übung
-
Benenne die Fachbegriffe der Graphen einer Scharfunktion.
TippsWie in der Zeile eines bekannten Kinderliedes (Amsel, Drossel, Fink und Star und die ganze Vogelschar) bezeichnet eine Schar eine Gruppe von mehreren Einzelnen.
LösungEine Kurvenschar besteht aus unendlich vielen Funktionsgraphen, die entstehen, wenn man verschiedene Werte für den Parameter in einer Scharfunktion einsetzt.
Eine Ortskurve ist ein Funktionsgraph, der durch gewisse charakteristische Punkte der Graphen einer Kurvenschar verläuft.
-
Gib bestimmte Funktionen einer Funktionsschar an.
TippsSetze den Wert von $t$ in den Funktionsterm ein und vereinfache.
Lösung- $t=1$
- $t=2$
- $t=4$
- $t=-2$
-
Leite die Scharfunktion ab.
TippsDer Paramter $t$ wird wie eine Zahl behandelt.
Lösung$f_t(x)=2t^2x^2+2tx$
$f^{\prime}_t(x)=2t^2\cdot 2 x+2t$
$x$ wird beim Ableiten zu $2x$ und $x$ zu $1$ (Potenzregel). Die Zahlen und der Parameter $t$ bleiben stehen und werden mit den Ableitungen multipliziert (Faktorregel).
Zusammenfassen: $f_t(x)=4t^2x+2t$
-
Beschreibe das Verfahren zur Bestimmung der Ortskurve.
TippsZuerst muss das Extremum in Abhängkeit des Parameters bestimmt werden. Dieser Schritt ist hier in drei Teilschritte unterteilt, die du als erstes in die richtige Reihenfolge bringen musst.
LösungBilde die ersten beiden Ableitungen:
$f_a(x)=x^2-2ax+2a^2$
$f_a^{\prime}(x)=2x-2a$
$f_a^{\prime\prime}(x)=2$
Setze die erste Ableitung gleich Null und berechne die Lösung.
$f_a^{\prime}(x)=0\implies 2x-2a=0 \implies x=a$
Setze die Lösung dieser Gleichung in die zweite Ableitung ein, um die Art des Extremums zu bestimmen und in die ursprüngliche Funktion, um den $y$-Wert zu bestimmen.
$f_a^{\prime\prime}(a)=2\implies f_a^{\prime\prime}(a)>0 \implies \text{ Tiefpunkt }$
$f_a(a)=a^2-2a\cdot a+2a^2=a^2$
Der Tiefpunkt hat die Koordinaten $T(a\vert a^2)$.
Zur Berechnung der Ortskurve schreibe die Koordinaten des Tiefpunktes in zwei Gleichungen:
$x=a$ und $y=a^2$.
Bilde aus den zwei Gleichungen eine Gleichung, in du $a=x$ in $y$ einsetzt:
$y=x^2$ ist die Ortskurve der Tiefpunkte.
-
Gib den Hochpunkt einer bestimmten Funktion an.
TippsSetze den Wert für $a$ ein und vereinfache.
LösungSetze $a=2$ in $f_a(x)=x^2-4ax+3a^2$ ein:
$f_2(x)=2^2-4\cdot 2x+3\cdot 2^2=x^2-8x+12$
Setze $a=2$ in $T(2a\vert -a^2)$ ein:
$T(2\cdot 2\vert -2^2)=T(4\vert -4)$
-
Bestimme den Extrempunkt und die Ortskurve.
TippsDie Koordinaten des Tiefpunkts hängen von $a$ ab, während die Ortskurve eine Funktion mit $y$ in Abhängigkeit von $x$ ist.
LösungBilde die ersten beiden Ableitungen:
$f_a(x)=x^2-4ax+3a^2$
$f_a^{\prime}(x)=2x-4a$
$f_a^{\prime\prime}(x)=2$
Setze die erste Ableitung gleich Null und berechne die Lösung.
$f_a^{\prime}(x)=0\implies 2x-4a=0 \implies x=2a$
Setze die Lösung dieser Gleichung in die zweite Ableitung ein, um die Art des Extremums zu bestimmen und in die ursprüngliche Funktion, um den $y$-Wert zu bestimmen.
$f_a^{\prime\prime}(2a)=2\implies f_a^{\prime\prime}(a)>0 \implies \text{ Tiefpunkt }$
$f_a(2a)=(2a)^2-4a\cdot 2a+3a^2=4a^2-8a^2+3a^2=-a^2$
Der Tiefpunkt hat die Koordinaten $T(2a\vert -a^2)$.
Zur Berechnung der Ortskurve schreibe die Koordinaten des Tiefpunktes in zwei Gleichungen:
$x=2a$ und $y=-a^2$.
Bilde aus den zwei Gleichungen eine Gleichung, in du die erste nach $a$ umformst: $a=\frac{x}{2}$ und diese in $y$ einsetzt:
$y=-\big(\frac{x}{2}\big)^2=-\frac{x}{4}$ ist die Ortskurve der Tiefpunkte.
9.369
sofaheld-Level
6.600
vorgefertigte
Vokabeln
8.220
Lernvideos
38.687
Übungen
33.508
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Klassenstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Quadratische Gleichungen – Übungen
- Flächeninhalt


 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?