Potenzgleichungen

Inhaltsverzeichnis zum Thema

• Was ist eine Potenzgleichung?
  • Potenzen
  • Die Potenzgleichung
• Potenzgleichungen mit natürlichen Exponenten
  • Gerade Exponenten
  • Beispiele
  • Ungerade Exponenten
• Potenzgleichungen mit rationalen Exponenten
  • Beispiel 1
  • Beispiel 2
  • Beispiel 3

Was ist eine Potenzgleichung?

Potenzen

In einer Potenzgleichung steht die unbekannte Größe $x$ in der Basis.

Wir wollen zunächst klären, was eine Potenz überhaupt ist. Eine Potenz ist eine abkürzende Schreibweise für ein Produkt, in welchem ein Faktor mehrmals vorkommt:

$a^n=\underbrace{a\cdot a\cdot ... \cdot a}_{\text{n-mal}}$.

Anstelle den Faktor $a$ also $n$-mal aufzuschreiben, können wir kurz $a^n$ schreiben.

Schauen wir uns die Bestandteile der Gleichung genauer an.

• $a\in \mathbb{R}$ ist die Basis.
• $n\in \mathbb{N}$ ist der Exponent.
• $a^n$ ist die Potenz oder der Potenzwert.

Die Potenzgleichung

Eine Potenzgleichung hat allgemein diese Form:

$a\cdot x^n=b$.

Die Anzahl der Lösungen einer Potenzgleichung hängt von dem Faktor $a$, dem Wert auf der rechten Seite $b$ und dem Exponenten $n$ ab. Der Faktor $a$ darf nicht gleich $0$ sein.

Potenzgleichungen mit natürlichen Exponenten

Zunächst einmal schauen wir uns Potenzgleichungen mit natürlichem Exponenten an. Dabei unterscheiden wir zwischen geraden und ungeraden Exponenten.

Gerade Exponenten

Potenzfunktionen mit geradem Exponenten haben eine bestimmte Form. Hier sehen wir die Parabeln zu $f(x)=x^2$ und $g(x)=x^4$.

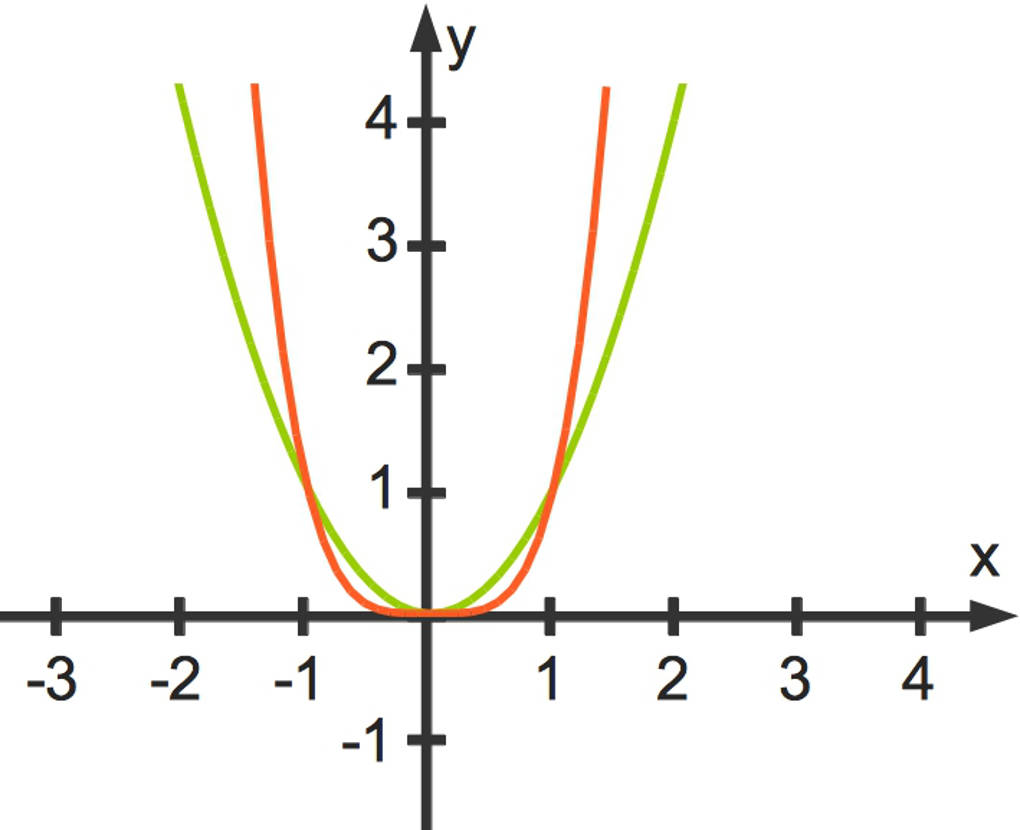
Du siehst, dass die Funktionsgraphen symmetrisch zur y-Achse sind. Das bedeutet, dass durchaus zwei verschiedene $x$-Werte zu dem gleichen Funktionswert $y$ führen können.

Anhand der Gleichung $3\cdot x^2=48$ soll gezeigt, wie eine Potenzgleichung gelöst wird:

1. Zuerst dividierst du auf beiden Seiten der Gleichung durch $3$. Dies ist eine Äquivalenzumformung. Dabei wird die Lösbarkeit der Gleichung nicht verändert und insbesondere auch nicht die Lösungsmenge. So erhältst du $x^2=16$.
2. Die Umkehrung von Quadrieren ist das Ziehen der Quadratwurzel. Beachte dabei, dass du in diesem Fall zwei Lösungen erhältst: $x=+\sqrt{16}=4$ und $x=-\sqrt{16}=-4$. Übrigens ist das Ziehen der Quadratwurzel keine Äquivalenzumformung.
3. Zuletzt kannst du die Lösungsmenge dieser Gleichung angeben: $\mathbb{L}=\{-4;4\}$.

Bei Potenzgleichungen der Form $a\cdot x^n=b$ mit geradem Exponenten $n$ können die folgenden Fälle vorliegen:

• $a>0$ und $b>0$, dann existieren genau zwei Lösungen: $\mathbb{L}=\left\{\pm\sqrt{\frac ba}\right\}$
• $a>0$ und $b<0$, dann existiert keine Lösung: $\mathbb{L}=\{\}$.
• $a<0$ und $b>0$, dann existiert ebenfalls keine Lösung: $\mathbb{L}=\{\}$.
• $a<0$ und $b<0$, auch hier existieren genau zwei Lösungen: $\mathbb{L}=\left\{\pm\sqrt{\frac ba}\right\}$.
• $b=0$, dann existiert immer genau eine Lösung, nämlich $x=0$: $\mathbb{L}=\{0\}$.

Potenzgleichungen mit geradem Exponenten können also entweder keine, eine oder zwei Lösungen haben. Am besten vollziehst du einmal die oben genannten Fälle Schritt für Schritt für dich nach.

Beispiele

Wenn du eine gerade Wurzel ziehst, musst du – wie bereits oben beschrieben – sowohl die positive als auch die negative Wurzel betrachten.

$\begin{array}{rclll} -5x^4&=&-80&|&:(-5)\\ x^4&=&16&|&\sqrt[4]{~~~}\\ x&=&\pm 2 \end{array}$

Die folgende Gleichung besitzt keine Lösung, weil die Wurzel einer negativen Zahl im Bereich der reellen Zahlen nicht definiert ist.

$\begin{array}{rclll} -5x^2+10&=&15&|&-10\\ -5x^2&=&5&|&:(-5)\\ x^2&=&-1 \end{array}$

Ungerade Exponenten

Potenzgleichungen mit ungeradem Exponenten haben immer genau eine Lösung. Dies liegt daran, dass der Funktionsgraph einer Potenzfunktion mit ungeradem Exponenten immer monoton steigend ist. Hier siehst du die Funktionsgraphen zu $h(x)=x^3$ und $i(x)=x^5$.

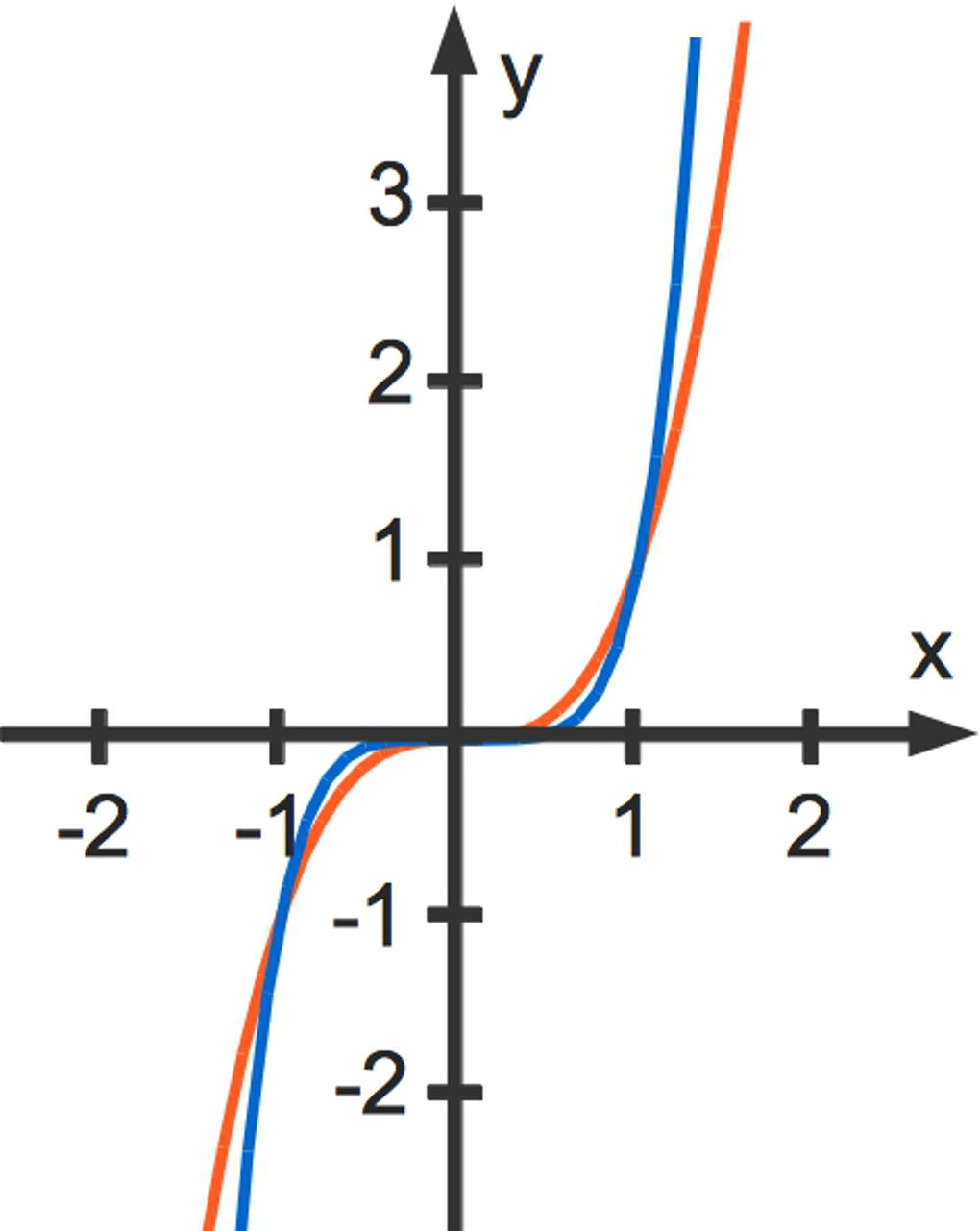
Beim Lösen einer solchen Gleichung gehst du so vor wie bei den Gleichungen mit geradem Exponenten.

$\begin{array}{rclll} -5x^3&=&-625&|&:(-5)\\ x^3&=&125&|&\sqrt[3]{~~~}\\ x&=&5 \end{array}$

Potenzgleichungen mit rationalen Exponenten

Zu guter Letzt schauen wir uns noch Potenzgleichungen mit rationalen Exponenten an. Deren Exponent besteht also aus einem Bruch. Du kannst dir merken, dass du eine Potenzgleichung mit rationalem Exponent löst, indem du die Gleichung auf beiden Seiten mit dem Kehrwert des Exponenten potenzierst.

Beispiel 1

$\begin{array}{rclll} x^\frac12&=&7&|&(~~~)^2\\ x&=&49 \end{array}$

Das Quadrieren ist keine Äquivalenzumformung! Das bedeutet, dass du dein Ergebnis überprüfen musst: $49^\frac12=\sqrt{49}=7$. ✓

Beispiel 2

$\begin{array}{rclll} x^\frac12&=&-7&|&(~~~)^2\\ x&=&49 \end{array}$

Allerdings ist $49^\frac12=\sqrt{49}=7$ und nicht $-7$. Diese Gleichung besitzt keine Lösung.

Beispiel 3

$\begin{array}{rclll} x^\frac32&=&8&|&(~~~)^\frac23\\ x&=&\sqrt[3]{8^2}\\ &=&\sqrt[3]{64}\\ &=&4 \end{array}$

Du weißt sicher noch, dass eine Potenz mit einem rationalen Exponenten eine Wurzel ist. Das bedeutet, dass du die Umformungen zum Lösen einer Potenzgleichung mithilfe der Potenzgesetze und Wurzelgesetze durchführen kannst.