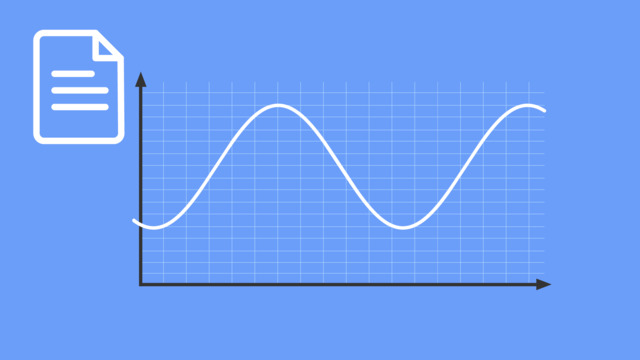
Periodische Vorgänge – Schaubilder interpretieren

Periodische Vorgänge – Schaubilder interpretieren Übung

• Gib den Maximalwert, die Amplitude sowie die Periodenlänge an.

  Tipps

  Die Einheit für den Wasserstand, für das Maximum, das Minimum sowie die Amplitude ist jeweils Meter.

  Die Einheit für die Periodenlänge sind Stunden.

  Die Werte für das Maximum sowie das Minimum sind auch angegeben.

  Die Amplitude berechnet sich wie folgt:

  $\frac{\text{Max }-\text{ Min}}2$.

  Die Periodenlänge ist der Abstand zweier Maxima oder Minima zueinander.

  Lösung

  Hier in dem Bild sind bereits das Minimum ($2~m$) sowie das Maximum ($5,2~m$) zu erkennen.

  Die Periodenlänge lässt sich am einfachsten als Abstand zwischen zwei Minima (oder zwei Maxima) bestimmen.

  Hier ist zu erkennen, dass ein Minimum bei $21$ Uhr und ein weiteres bei $9$ Uhr liegt. Also ist die Periodenlänge $12$ Stunden.

  Die Amplitude ist die Differenz von Maximum und Minimum dividiert durch $2$, also hier

  $\frac{5,2~m-2~m}{2}=\frac{3,2~m}{2}=1,6~m$.

• Beschreibe, wie die Zeit, in welcher das Ausflugschiff in den Hafen hineinfahren könnte, ermittelt werden kann.

  Tipps

  Das Ausflugschiff wird sicher nur tagsüber in den Hafen einfahren.

  Vielleicht hilft dir diese Skizze weiter!

  Beachte: Der Wasserstand muss $3~m$ oder mehr betragen.

  $x=3$ entspricht $3:00$ Uhr mitten in der Nacht. Da schläft der Kapitän noch.

  Lösung

  Dieser Graph zeigt die Veränderung des Wasserspiegels in Abhängigkeit der Uhrzeit. Der Graph verhält sich periodisch und wiederholt sich alle $12$ Stunden.

  Mit $5,2~m$ nimmt die Funktion den höchsten und mit $2~m$ den kleinsten Wert an.

  Wenn man wissen will von wann bis wann der Wasserstand $3~m$ oder mehr beträgt, kann man eine Gerade parallel zur x-Achse durch $y=3$ zeichnen. Dort, wo diese Gerade den Graphen schneidet, sind die Stellen, an welchen der Wasserstand genau $3~m$ beträgt.

  Der Funktionsgraph muss oberhalb dieser Linie liegen. Dann ist der Wasserstand höher oder gleich $3~m$ und somit hoch genug für das Schiff.

  Man kann die Zeiten ungefähr ablesen:

  • $23:20-6:40$ sowie
  • $11:20-18:40$.

  Da das Ausflugsschiff sicher nur tagsüber den Hafen anlaufen wird, kann die untere Zeit genommen werden.

  Dies ist die Info für den Kapitän: „Sie können ab $11:20$ Uhr in den Hafen einfahren und dort bis $18:40$ Uhr bleiben.“

• Ermittle das Minimum, das Maximum, die Amplitude sowie die Periodenlänge.

  Tipps

  Die Amplitude ist gegeben durch

  $\frac{\text{Max }-\text{ Min}}{2}$.

  Die Periodenlänge ist der Abstand zweier Maxima oder Minima.

  Nach einer Periodenlänge wiederholt sich der Vorgang.

  Lösung

  Die Entwicklung der Wassertemperatur in einem Heißwasserbehälter ist ein periodischer Vorgang:

  Das Wasser wird auf eine Temperatur erhitzt, dies ist das Maximum $90^\circ$, und kühlt dann ab. Ab einer gewissen Temperatur, dies ist das Minimum $60^\circ$, wird das Wasser wieder erhitzt.

  Die Abkühlung dauert $10~min$ und die Erhitzung $5~min$, gesamt sind dies $15~min$. Dies ist die Periodendauer.

  Es bleibt noch die Amplitude. Diese lässt sich wie folgt berechnen:

  $\frac{\text{Max }-\text{ Min}}{2}=\frac{90^\circ-60^\circ}{2}=\frac{30^\circ}{2}=15^\circ$.

• Untersuche wie lange jeweils das Wasser eine günstige Temperatur für Grüntee hat.

  Tipps

  Beachte: Wenn du ein Zeitintervall gefunden hast, wiederholt sich dieses immer nach einer Periodenlänge.

  Die Periodenlänge beträgt hier $15$ Minuten.

  Drei Antworten sind richtig.

  Lösung

  Die Temperaturen in dem Heißwasserbehälter variieren zwischen $60^\circ$ und $90^\circ$. Alle Temperaturen oberhalb von $75^\circ$ sind für einige Grüntees zu hoch. Der Tee wird dann recht bitter und schmeckt nicht mehr.

  Wenn man wissen will, zu welchen Zeiten die Wassertemperatur $75^\circ$ oder weniger beträgt, zeichnet man eine parallele Gerade zu horizontalen Achse durch $75^\circ$. Dies ist hier zu sehen.

  Überall dort, wo der Graph unterhalb dieser Geraden liegt, ist die Temperatur in Ordnung. Beispielhaft ist hier das Intervall $[5;12,5]$ markiert. Da der Vorgang periodisch ist, wiederholt sich dieses Intervall in immer gleichen Abständen, nämlich $15$ Minuten.

  Also kann der grüne Tee

  • von Minute $5$ bis $12,5$,
  • von Minute $20$ bis $27,5$,
  • von Minute $35$ bis $42,5$,
  • ...

  aufgegossen werden.

  Zum Glück sind solche Heißwasserbehälter oft an die Wasserleitung angeschlossen, sonst müsste man immer wieder Wasser nachfüllen.

• Gib die Formel zur Berechnung der Amplitude an.

  Tipps

  Die Amplitude ist die maximale Ausdehnung bei einer periodischen Funktion ausgehend vom arithmetischen Mittel von Maximum und Minimum.

  Das arithmetische Mittel von Maximum und Minimum berechnet sich wie folgt

  $\frac{\text{Max }+\text{ Min}}{2}$.

  Die Amplitude ist positiv.

  Lösung

  Die Amplitude ist die maximale Ausdehnung bei einer periodischen Funktion ausgehend vom arithmetischen Mittel von Maximum und Minimum.

  Das arithmetische Mittel ist in dem Schaubild durch die gestrichelte horizontale rote Linie (bei $y=3,6$) angedeutet.

  Die Amplitude lässt sich wie folgt berechnen:

  Amplitude$=\frac{\text{Max }-\text{ Min}}{2}$.

  Also: Man bildet die Differenz von Maximum und Minimum und dividiert diese Differenz durch $2$.

• Ordne dem periodischen Vorgang seiner Periodenlänge und Amplitude zu.

  Tipps

  Achte auf die Einheiten.

  Die Amplitude entspricht der maximalen Ausdehnung des Lungenvolumens ausgehende von dem arithmetischen Mittel (rot gestrichelt eingezeichnet).

  Nach einer Periodenlänge (Zeit) wiederholt sich die Atmung wieder.

  Die Amplitude ist vertikal und die Periodenlänge horizontal einzuzeichnen.

  Verwende für die Amplitude

  $=\frac{\text{Max }-\text{ Min}}{2}$.

  Lösung

  Das Maximum ist hier $6,5~l$ und das Minimum $1,2~l$.

  Damit ist die Amplitude

  $\frac{6,5~l-1,2~l}2=2,65~l$.

  Die Periode ist gegeben durch

  $\frac{60~s}{20}=3~s$.