Volumen und Oberfläche von Pyramiden, Kegeln und Kugeln
Hast du schon einmal eine Pyramide gesehen? Vielleicht auf einem Bild oder sogar schon mal direkt: In Ägypten stehen Pyramiden. Pyramiden können verschiedene Grundflächen haben.
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
Was ist eine Pyramide?
Eine Pyramide ist ein geometrischer Körper. Sie hat eine Spitze und eine Grundfläche. Die Grundfläche kann ein Rechteck, Dreieck oder ein beliebiges n-Eck sein. Jeder Eckpunkt der Grundfläche wird mit der Spitze der Pyramide verbunden.
Je nach Art der Grundfläche unterscheidet man verschiedene Pyramiden.
Rechteckige Grundfläche
Hier siehst du links das Schrägbild und rechts das Netz einer Pyramide mit quadratischer Grundfläche.

Daran kannst du einige Eigenschaften erkennen.
- Die Anzahl der Flächen: Eine rechteckige Pyramide besteht aus fünf Flächen, nämlich der rechteckigen Grundfläche sowie vier Seitenflächen. Diese sind Dreiecke. Die Seitenflächen ergeben zusammen die Mantelfläche.
- Die Anzahl der Ecken: Eine Pyramide mit rechteckiger Grundfläche hat insgesamt fünf Ecken, vier Ecken der rechteckigen Grundfläche sowie die Spitze.
- Die Anzahl der Kanten: Die rechteckige Grundfläche hat vier Kanten als Übergang zu den Seitenflächen. Jeweils zwei Seitenflächen haben eine gemeinsame Kante. Insgesamt sind dies acht Kanten.
Wo findest du rechteckige Pyramiden in deiner Umgebung?
- Die Dächer von Kirchtürmen haben oft die Form einer Pyramide.
- Sicher hast du auch schon einmal von den ägyptischen Pyramiden gehört oder Bilder von diesen Pyramiden gesehen. Schon die alten Ägypter kannten die geometrische Form der Pyramide.
Weitere Grundflächen
- Wenn die Grundfläche ein Dreieck ist, spricht man von einem Tetraeder.
- Eine Pyramide mit einer fünfeckigen Grundfläche wird als fünfeckige Pyramide bezeichnet.
Ist die jeweilige Grundfläche regelmäßig, so heißt auch die Pyramide regelmäßig. Zum Beispiel ist eine quadratische Pyramide eine regelmäßige Pyramide.
Schauen wir uns nun einige Beispiele etwas genauer an.
Quadratische Pyramiden
Schauen wir uns noch einmal das Schrägbild sowie das Netz einer quadratischen Pyramiden mit den zugehörigen Beschriftungen an.
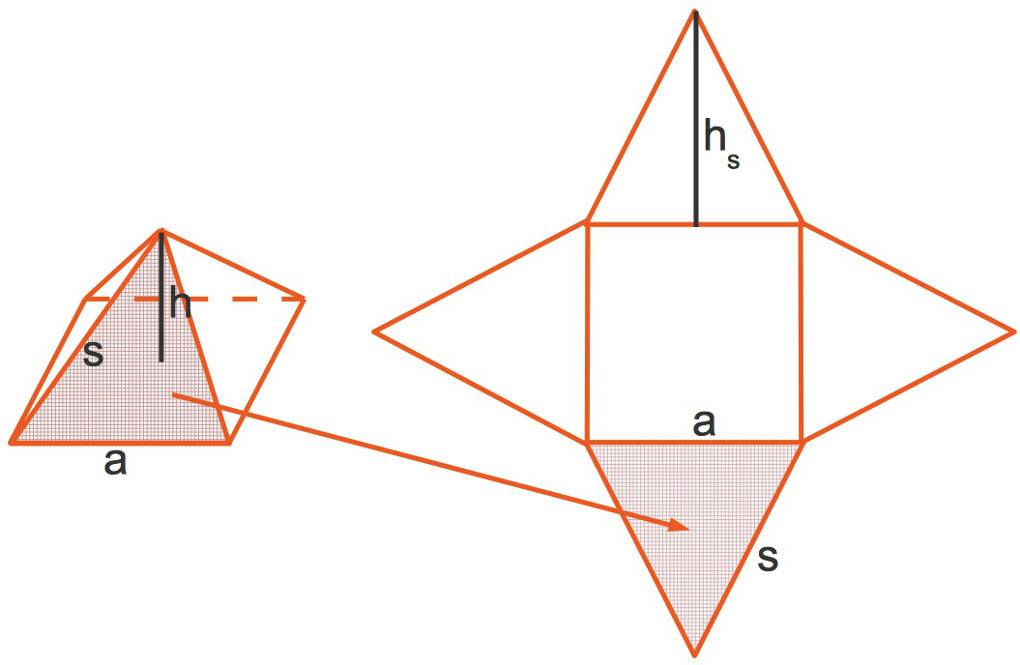
- Die Höhe der Pyramide wird mit $h$ bezeichnet. Diese erhältst du, indem du das Lot von der Spitze der Pyramide auf deren Grundseite fällst.
- Die Seitenlänge $s$ ist die Länge eines Schenkels eines Seitendreiecks. Diese sind alle gleichschenklig, wenn sich die Spitze senkrecht über dem Mittelpunkt der Grundfläche befindet. Eine solche Pyramide wird gerade Pyramide genannt.
- Die Seitenlänge der Grundfläche wird mit $a$ bezeichnet.
- Die Höhe der vier Seitendreiecke ist jeweils gleich groß. Sie wird mit $h_s$ bezeichnet.
Das Volumen einer quadratischen Pyramide
Allgemein ist das Volumen einer Pyramide gegeben durch die Formel
$V=\frac13\cdot G\cdot h$.
Dabei ist $G$ der Inhalt der Grundfläche.
Also gilt für eine quadratische Pyramide
$V=\frac13\cdot a^2\cdot h$.
Die Mantel- sowie Oberfläche einer quadratischen Pyramide
Die Mantelfläche ergibt sich als Summe der Seitenflächen. Da bei einer quadratischen Pyramide dies vier gleichschenklige Dreiecke mit der Höhe $h_s$ und der Grundseite $a$ sind, erhält man
$M=4\cdot \frac12\cdot a\cdot h_s=2\cdot a\cdot h_s$.
Die Oberfläche erhältst du, wenn du zu der Mantelfläche die Grundfläche addierst: $O=M+G$, also für eine quadratische Pyramide
$O=2\cdot a\cdot h_s+a^2=a\cdot (a+2h_s)$.
Beispiel
Die Pyramide auf dem Marktplatz von Karlsruhe ist das Grabmal des Stadtgründers Karl Wilhelm von Baden-Durlach (1679–1738) und das Wahrzeichen der Stadt.
Ihre Seitenkantenlängen betragen $s=8,04~m$ und die Länge der Grundseite $a=6,05~m$.
Berechnung der Mantelfläche: Die Pyramide soll neu gestrichen werden. Wie groß ist die zu streichende Fläche? Hier ist nach der Mantelfläche gefragt, da der Boden ja nicht gestrichen wird.
Du verwendest die Formel $M=2\cdot a\cdot h_s$. Allerdings kennst du $h_s$ nicht, die Höhe eines Seitendreiecks. Schaue dir die Skizze zu einem solchen Seitendreieck an. Insbesondere ist hier das halbe Seitendreieck, welches rechtwinklig ist, (rechts) von Bedeutung.
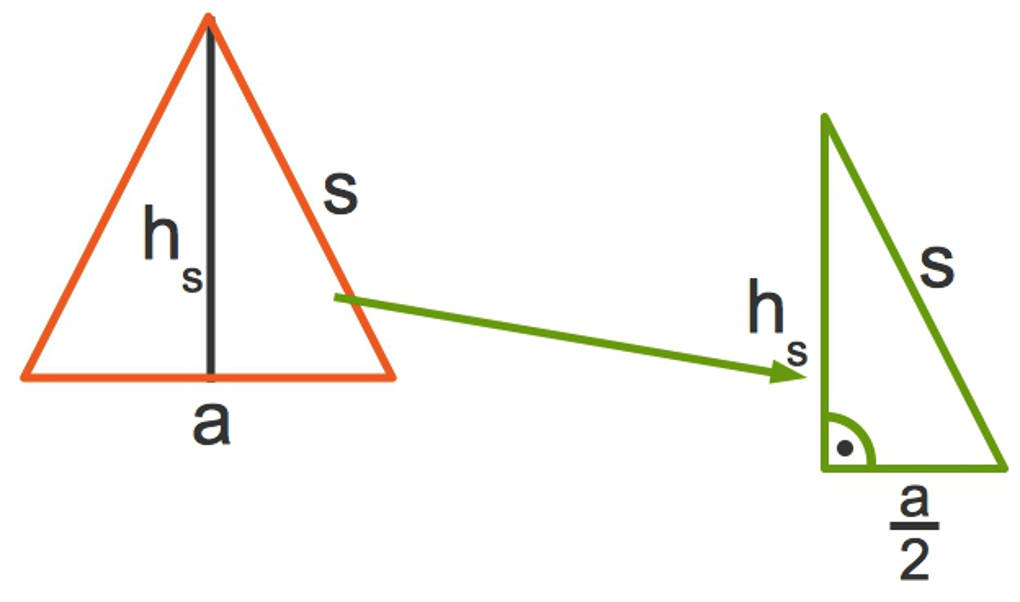
Nun kannst du den Satz des Pythagoras verwenden zur Berechnung von $h_s$
$\left(\frac a2\right)^2+h_s^2=s^2$.
Diese Gleichung kannst du nach $h_s$ umformen zu
$h_s=\sqrt{s^2-\left(\frac a2\right)^2}$.
Setze nun die bekannten Größen ein. So erhältst du $h_s\approx 7,45~m$.
Die Mantelfläche beträgt also
$M=6,05~m\cdot 2\cdot 7,45~m\approx 90,15~m^2$.
Die Höhe der Pyramide: In der Pyramide soll genau in der Mitte eine $6,50~m$ hohe Pflanze aufgestellt werden. Passt diese in die Pyramide? Hier ist nach der Höhe gefragt. Der Einfachheit halber wird die Ausdehnung der Pflanze außer Acht gelassen und nur deren Höhe betrachtet.
Um die Höhe der Pyramide zu berechnen, verwendest du den Parallelschnitt, ein gleichschenkliges Dreieck, welches entsteht, wenn du parallel zu einer Grundseite durch die Spitze der Pyramide schneidest. Der halbe Parallelschnitt ist wieder ein rechtwinkliges Dreieck.
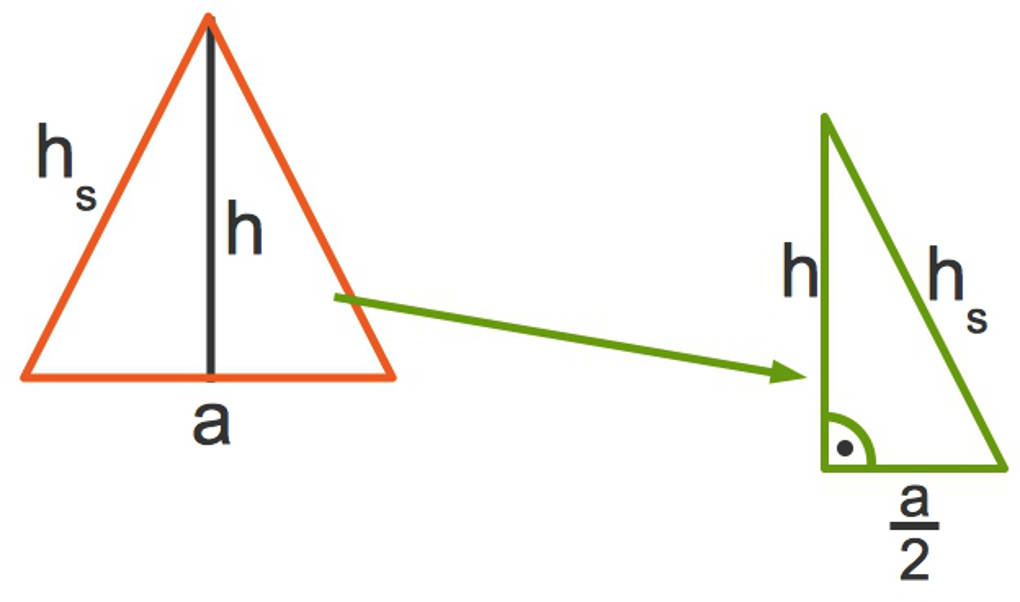
Du verwendest noch einmal den Satz des Pythagoras und formst diesen nach $h$ um.
$h=\sqrt{h_s^2-\left(\frac a2\right)^2}$
Einsetzen der bekannten Größen führt zu $h\approx 6,81~m$. Das bedeutet, dass die Pflanze in die Pyramide passt.
Was sind platonische Körper?
Platonische Körper, auch Platon’sche Körper, zeichnen sich dadurch aus, dass sie ausschließlich von gleichseitigen, kongruenten Vielecken eines Typs begrenzt werden.
Jedem dieser Körper ordnete Platon (ca. 428 - 348 v. Chr.) eines der Elemente des altgriechischen Kosmos zu. Damit stellten diese Körper in der griechischen Weltsicht die Bausteine des gesamten Kosmos dar.
Heutzutage findet man alle diese Körper, wegen ihrer besonderen Eigenschaft, als „Würfel“ von Gesellschaftsspielen.
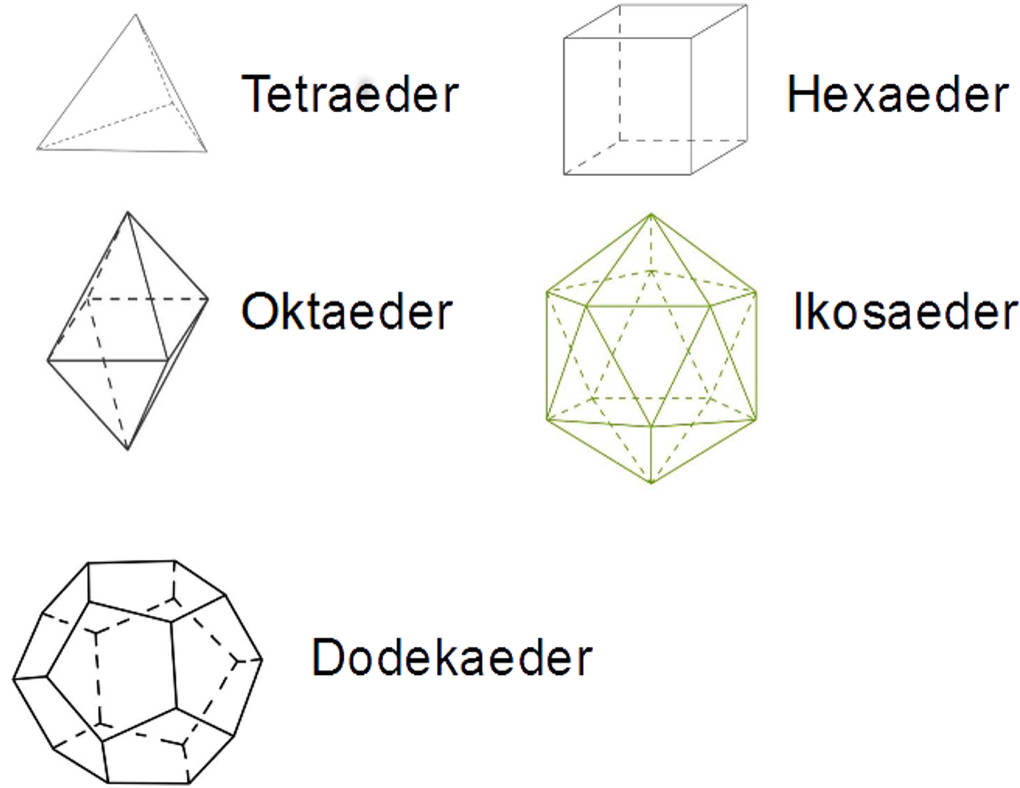
Es gibt nur fünf platonische Körper.
- Das Tetraeder oder Vierflächner: Es wird durch vier gleichseitige Dreiecke begrenzt. Zuordnung: Feuer.
- Das Hexaeder, Sechsflächner, der Würfel: Der Würfel wird begrenzt durch sechs Quadrate. Zuordnung: Erde.
- Das Okateder oder Achtflächner: Es wird begrenzt durch acht gleichseitige Dreiecke. Du kannst dir ein Oktader vorstellen wie eine doppelte quadratische Pyramide. Zuordnung: Luft.
- Das Dodekaeder oder Zwöfflächner: Es wird begrenzt durch zwölf regelmäßige Fünfecke. Zuordnung: Quintessenz – der Himmelsäther.
- Das Ikosaeder oder Zwanzigflächner: Es wird begrenzt durch zwanzig gleichseitige Dreiecke. Zuordnung: Wasser.
Tetraeder
Ein Tetraeder, oder auch Vierflächner, ist ein platonischer Körper. Es wird durch vier gleichseitige und kongruente Dreiecke begrenzt. Ein Tetraeder besitzt
- vier gleichseitige Dreiecke als Seitenflächen,
- sechs (gleich lange) Kanten sowie
- vier Ecken, in denen je drei Flächen aufeinandertreffen.

Die Oberfläche eines Tetraeders
Die Seitenlänge sei $a$. Dann kann mit Hilfe der folgenden Formeln die Oberfläche eines Tetraeders berechnet werden.
- Die Höhe eines Seitendreiecks ist gegeben durch $h_s=\frac{\sqrt 3}{2}a$.
- Damit kann die Fläche eines Seitendreiecks berechnet werden $A=\frac{\sqrt 3}4a^2$.
- Somit ist die Oberfläche des Tetraeders gegeben durch $O=4\cdot A=\sqrt 3\cdot a^2$.
Das Volumen eines Tetraeders
- Die Höhe eines Tetraeders ist gegeben durch $h=\frac{\sqrt 6}3a$.
- Damit kann das Volumen des Tetraeders berechnet werden: $V=\frac13\cdot A\cdot h$, wobei $A$ die Fläche eines Seitendreiecks ist. Also gilt
$\quad~~~V=\frac13\cdot \frac{\sqrt 3}4a^2\cdot \frac{\sqrt 6}3a=\frac{\sqrt 2}{12}a^3$.
Beispiel
Es gibt Trinkpakete in Form eines Tetraeders. Wie lang ist die Grundseite $a$, wenn das Fassungsvermögen dieser Trinkpakete $330~ml~\hat =~330~cm^3$ beträgt?
Du verwendest die Volumenformel und formst diese nach $a$ um.
$\begin{array}{rclll} \frac{\sqrt 2}{12}a^3&=&330&|&\cdot 12~|~:\sqrt 2\\ a^3&=&\frac{330\cdot 12}{\sqrt 2}&|&\sqrt[3]{~~~}\\ a&=&\sqrt[3]{\frac{330\cdot 12}{\sqrt 2}}\\ &\approx&14,1 \end{array}$
Die Grundseite hat also die Länge $14,1~cm$.
Oktaeder
Das Oktaeder oder Achtflächner ist einer der fünf platonischen Körper. Ein Oktaeder besitzt
- acht gleichseitige Dreiecke als Seitenflächen,
- zwölf (gleich lange) Kanten sowie
- sechs Ecken, in denen je vier Flächen aufeinandertreffen.
Das Oktaeder ist eine gleichseitige vierseitige Doppelpyramide mit quadratischer Grundfläche.
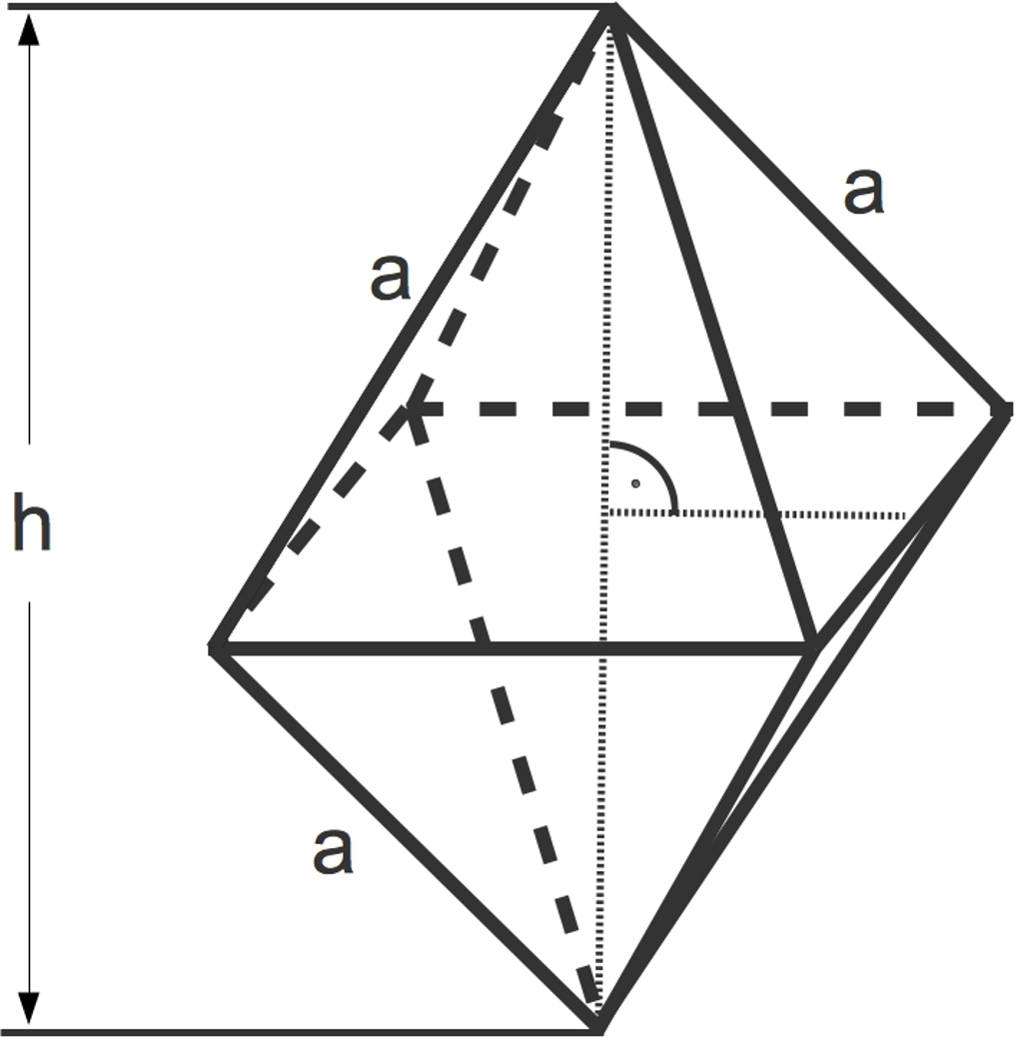
Damit ist die Oberfläche eines Oktaeders das Doppelte des Mantels einer Pyramide mit quadratischer Grundfläche.
- Die Höhe eines Seitendreiecks ist gegeben durch $h_s=\frac{\sqrt 3}{2}a$.
- Damit kann die Fläche eines Seitendreiecks berechnet werden $A=\frac{\sqrt 3}4a^2$.
- Somit ist die Oberfläche des Oktaeders gegeben durch $O=8\cdot A=2\sqrt 3\cdot a^2$.
Ebenso ist das Volumen eines Oktaeders das Doppelte des Volumens einer Pyramide mit quadratischer Grundfläche.
- Die Höhe der Pyramide ist gegeben durch $h=\frac{1}{\sqrt 2}a$.
- Damit kann das Volumen des Oktaeders berechnet werden durch:
$\quad ~~~V=2\cdot \frac13\cdot a^2\cdot \frac{1}{\sqrt 2}a=\frac{\sqrt 2}{3}a^3$.
Was ist ein Kegel?
Ein Kegel ist ein geometrischer Körper.
- Die Grundfläche eines Kegels ist ein Kreis.
- Jeder Punkt des Kreisrandes wird mit der Spitze des Kegels verbunden.
Ein Kegel hat somit
- eine Ecke, dies ist die Spitze,
- eine Kante, den Rand des Kreises als Grundfläche, sowie
- zwei Flächen.
Die Flächen eines Kegels
Ein Kegel besteht aus
- einem Kreis als Grundfläche sowie
- einem Kreisausschnitt als Mantel.
Beispiele für Kegel
- Eine Eistüte hat die Form eines Kegels.

- Kannst du dich noch an die Schultüte bei deiner Einschulung erinnern? Auch die hat häufig die Form eines Kegels.
Verschiedene Kegel
Es gibt gerade Kegel und schräge Kegel.
Gerade Kegel
Hier siehst du einen geraden Kegel.
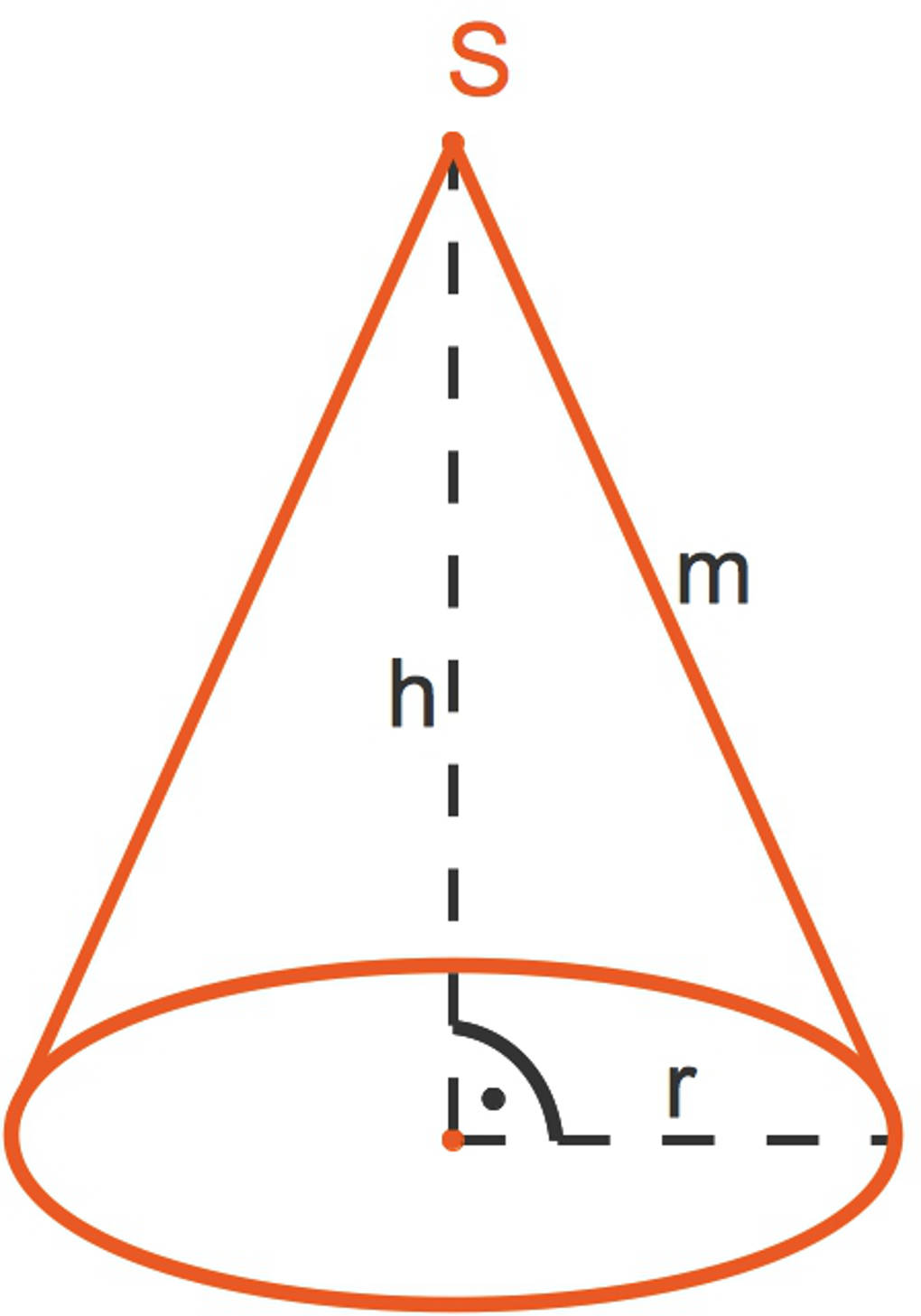
- $S$ ist die Spitze des Kegels. Diese liegt bei einem geraden Kegel genau senkrecht über dem Mittelpunkt des Grundkreises.
- $m$ ist die Mantellinie. Die Mantellinie ist bei einem geraden Kegel immer gleich lang.
- $h$ ist die Höhe des Kegels. Dies ist der Abstand der Spitze zu der Grundfläche. Im Falle des geraden Kegels ist das gerade der Abstand der Spitze zu dem Mittelpunkt des Grundkreises.
- $r$ ist der Radius des Grundkreises.
Schräge Kegel
Hier siehst du einen schrägen Kegel.
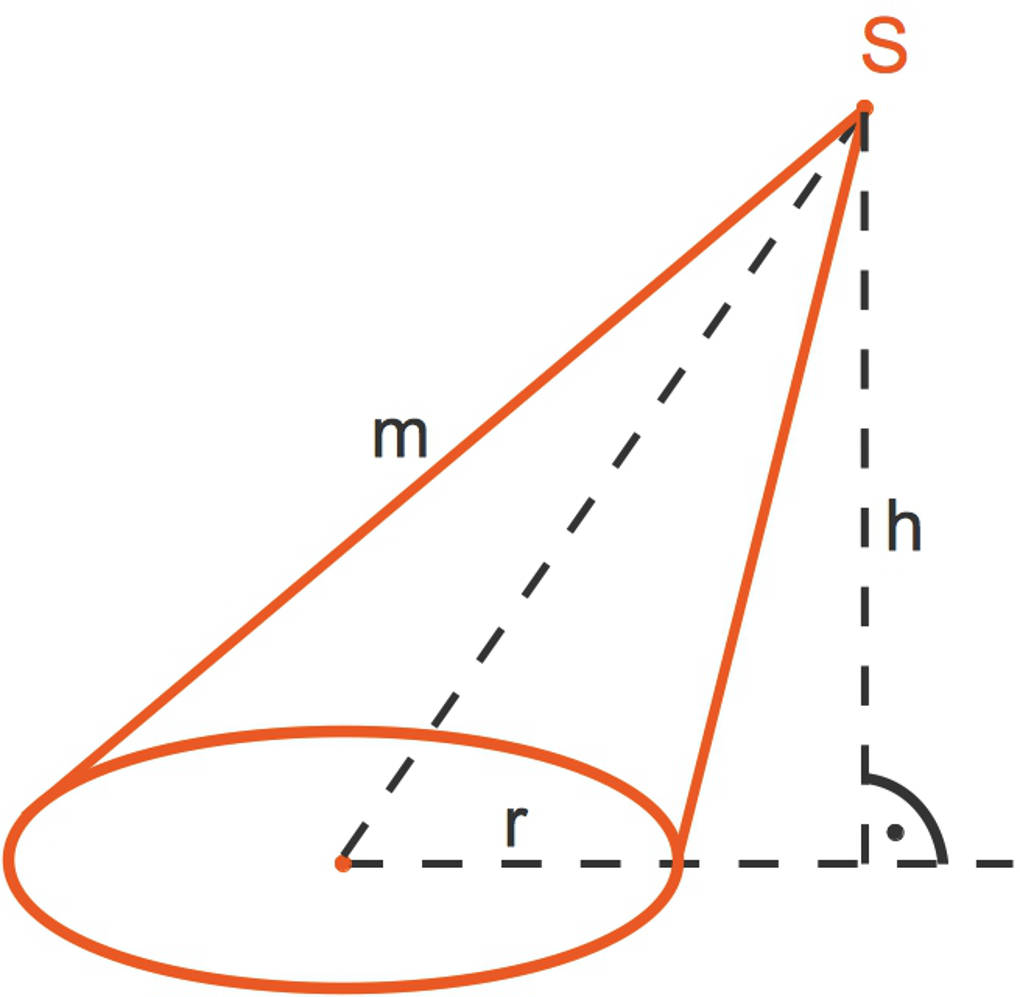
- Im Gegensatz zum geraden Kegel liegt die Spitze nicht senkrecht über dem Mittelpunkt des Grundkreises.
- Die Mantellinien sind bei einem schrägen Kegel nicht gleich lang. Du kannst erkennen, dass die (eingezeichnete) linke Mantellinie länger ist als die rechte.
Zum Beispiel erzeugt eine Lichtquelle einen Lichtkegel. Wenn die Lichtquelle nicht senkrecht nach unten zeigt, entsteht so ein schräger Kegel.

Im Folgenden beschäftigen wir uns mit der Mantelfläche, der Oberfläche und dem Volumen von geraden Kegeln. Bei schrägen Kegeln ist die Berechnung von Mantel- und Oberfläche etwas komplizierter.
Die Mantel- und Oberfläche eines Kegels
Die Oberfläche eines Kegels setzt sich aus der Grundfläche und der Mantelfläche zusammen.
Die Grundfläche
Die Grundfläche eines Kegels ist ein Kreis. Dessen Flächeninhalt kannst du mit Hilfe des Radius $r$ berechnen: $A_G=\pi\cdot r^2$.
Dabei ist $\pi=3,1415...$ die sogenannte Kreiszahl.
Die Mantelfläche
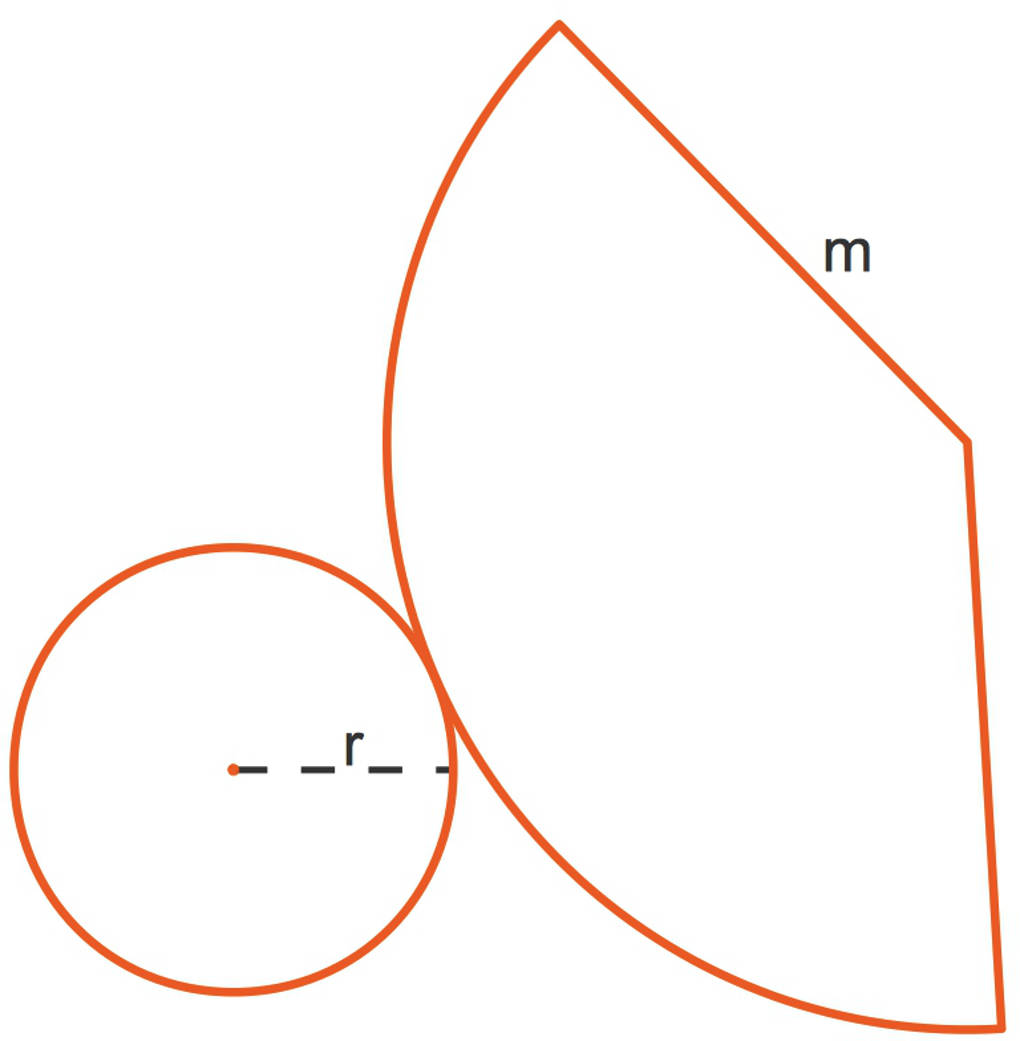
Wie berechnest du die Mantelfäche eines Kegels? Wenn du einen Kegel entlang der Mantellinie aufschneidest, erhältst du den hier zu erkennenden Kreisausschnitt (rechts). Umgekehrt, wenn du einen solchen Kreisausschnitt wieder zusammenlegst, erhältst du einen Kegel. Probiere es doch einmal aus. Der Radius dieses Kreisausschnittes ist die Mantellinie $r_\circ=m$.
Die Mantelfläche $M$ ist die Fläche dieses Kreisausschnittes.
Der Flächeninhalt des gesamten Kreises ist $A_{\circ}=\pi\cdot m^2$. Nun müssen wir uns noch überlegen, wie groß der Anteil des Kreisausschnittes an dem gesamten Kreis ist.
Es gilt
$\frac{M}{A_\circ}=\frac{b}{u_\circ}$,
wobei
- $b$ die Bogenlänge des Kreisausschnittes ist. Diese ist gleich dem Umfang des Grundkreises $u_G=2\cdot \pi\cdot r$.
- Darüber hinaus ist $u_\circ=2\cdot \pi\cdot m$.
Nun können wir dies in die obige Gleichung einsetzen und dann nach $M$ umformen:
$\begin{array}{rclll} \frac{M}{\pi\cdot m^2}&=&\frac{\not 2\cdot \not \pi\cdot r}{\not 2\cdot \not \pi\cdot m}&|&\cdot \pi\cdot m^2\\ M&=&\pi\cdot r\cdot m \end{array}$
Dies ist die gesuchte Mantelfläche.
Die Oberfläche
Die Oberfläche eines Kegels ergibt sich als die Summe von Mantel- und Grundfläche: $O=\pi\cdot r^2+\pi\cdot r\cdot m=\pi\cdot r\cdot (r+m)$.
Das Volumen eines Kegels
Das Volumen eines Kegels kannst du mit Hilfe der folgenden Formel berechnen:
$V=\frac13\cdot\pi\cdot r^2\cdot h$.
$h$ ist die Höhe des Kegels.
Beispiel – Paul bastelt eine Schultüte
Paul isst gerade ein Eis. Beim Anblick seiner kegelförmigen Eistüte denkt er daran, dass er seiner Schwester eine Schultüte basteln will. Diese soll $h=80~cm$ hoch sein und einen Kreis mit dem Radius $r=15~cm$ als Grundfläche haben. Wie viel Pappkarton benötigt er, um die Schultüte zu basteln? Dabei wird der Verschnitt nicht berücksichtigt. Er muss die Mantelfläche eines Kegels berechnen: $M=\pi\cdot r\cdot m$.
Leider kennt er $m$ noch nicht. Er fertigt sich eine Skizze an.
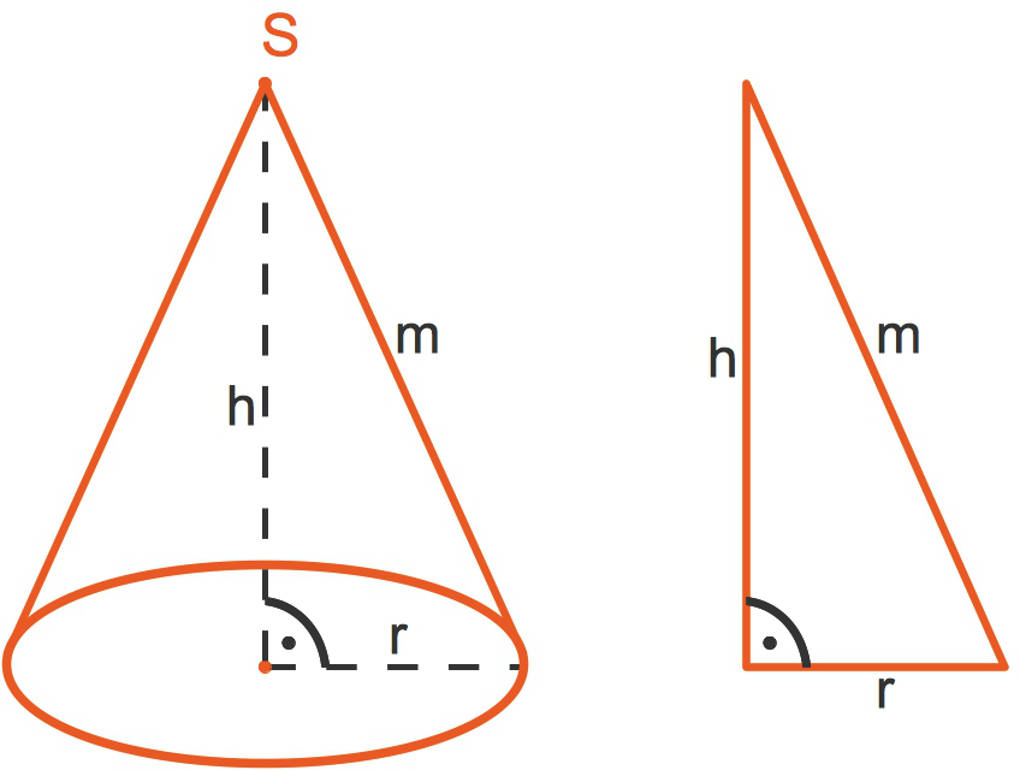
Dabei erkennt er, dass er den Satz des Pythagoras anwenden kann: $h^2+r^2=m^2$.
Er setzt die bekannten Größen ein und zieht die Wurzel:
$m=\sqrt{(80~cm)^2 +(15~cm)^2}=\sqrt{6625~cm^2}\approx 81,40~cm$.
Jetzt kann er die Formel für die Mantelfläche verwenden: $M\approx\pi\cdot (15~cm)\cdot (81,40~cm)\approx 3835,90~cm^2$.
Das weiß er jetzt und kann direkt von der Eisdiele zu dem Bastelladen gehen.
Beispiel – Wie viel Saft passt in ein kegelförmiges Glas?
Ein kegelförmiges Glas mit der Höhe $h=10~cm$ und dem Radius $r=3,5~cm$ wird mit Saft gefüllt. Dieses Mal ist nach dem Volumen gefragt:
$V=\frac13\cdot \pi\cdot (3,5~cm)^2\cdot (10~cm)\approx y128~cm^3$.
Dies entspricht $0,128~L$. So viel passt in das Glas hinein. Wenn du bedenkst, dass das Glas nicht ganz gefüllt wird, passt also etwas mehr als $0,1~L$ hinein.
Der Kegelstumpf
Du erhältst einen Kegelstumpf, wenn du von einem Kegel einen kleineren Kegel an der Spitze parallel zur Grundfläche abschneidest.
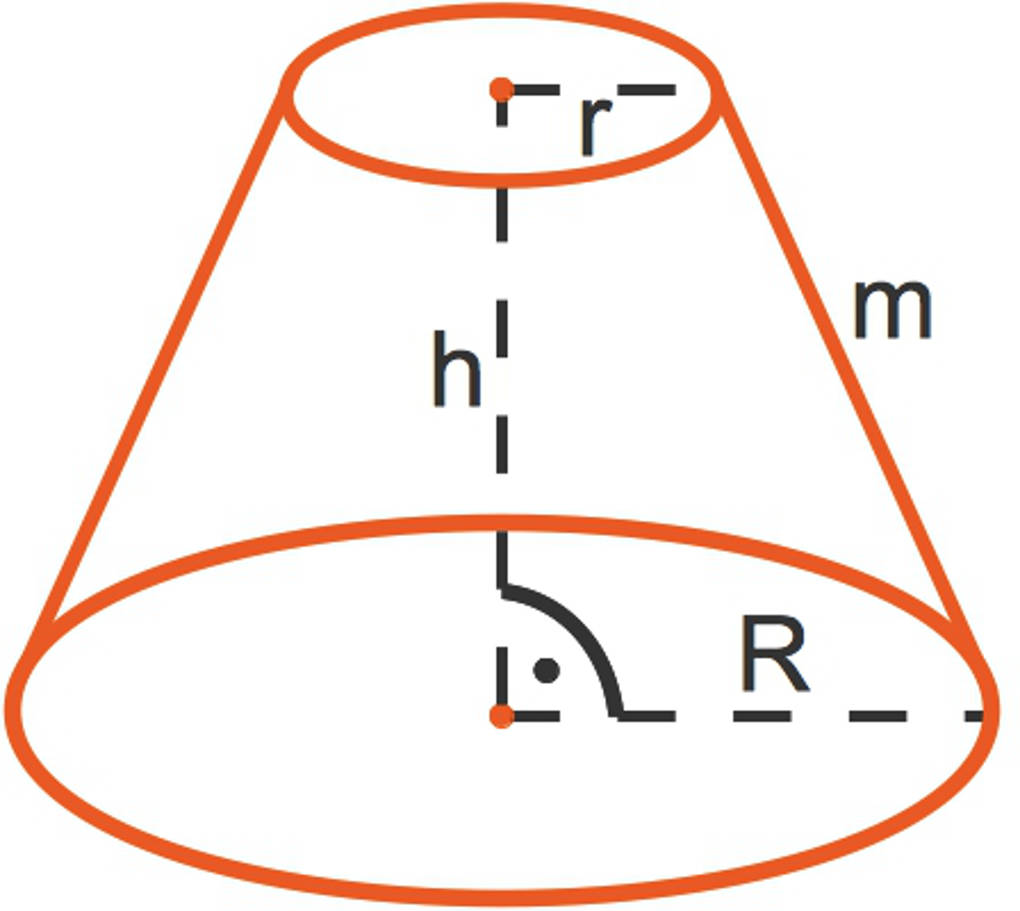
- Ein Kegelstumpf hat im Gegensatz zu einem Kegel neben einer Grundfläche mit dem Radius $R$ auch noch eine Deckfläche mit dem Radius $r < R$.
- Die Höhe des Kegelstumpfes ist $h$, der Abstand von Grund- zu Deckfläche.
- $m$ ist die Mantellinie des Kegelstumpfes.
Die Mantel- und Oberfläche eines Kegelstumpfes
- Der Flächeninhalt der Grundfläche beträgt $A_G=\pi\cdot R^2$ und der
- der Deckfläche $A_D=\pi\cdot r^2$.
Die Mantelfläche kannst du mit der Formel $M=\pi\cdot m\cdot (R+r)$ berechnen.
Die Oberfläche erhältst du, wenn du zu der Mantelfläche die Grund- und Deckfläche addierst: $O=\pi\cdot (R^2+r^2+m\cdot(R+r))$.
Das Volumen eines Kegelstumpfes
Für die Berechnung des Volumens verwendest du die Formel
$V=\frac13\cdot \pi\cdot h\cdot(R^2+R\cdot r+r^2)$.
Beispiel
Beim Schulfest der Schule C. F. Gauss soll eine besonders knifflige Aufgabe gelöst werden.
Ein Kegelstumpf mit einem Volumen von $3500~dm^3$, der Höhe $h=45~dm$ und einem Radius des größeren Kreises, der doppelt so groß ist wie der kleinere, also $R=2r$, soll aus Metallplatten gebaut werden. Der Kegelstumpf soll auf der größeren Grundfläche stehen. Auch diese muss mit dem Material erstellt werden. Nach oben soll der Kegelstumpf offen sein.
Wie viel Material (in $dm^2$) wird für diesen Kegelstumpf benötigt?
Du musst die Mantelfläche berechnen und dazu die Grundfläche addieren.
Es ist $M=\pi\cdot m\cdot (R+r)=3\pi\cdot m\cdot r$. Es sind weder $r$ noch $m$ bekannt.
Mit dem bekannten Volumen
$3500~dm^3=\frac13\cdot \pi\cdot (45~dm)\cdot((2r)^2+r\cdot r+r^2)=6\pi\cdot (15~dm)\cdot r^2$
kann durch Division durch $6\pi\cdot (15~dm)$ und anschließendes Ziehen der Wurzel $r$ berechnet werden:
$r=\sqrt{\frac{3500~dm^3}{6\pi\cdot (15~dm)}}\approx 12,4~dm$.
Damit ist $R=24,8~dm$.
Nun muss noch $m$ berechnet werden. Hierfür verwendest du die folgende Skizze.
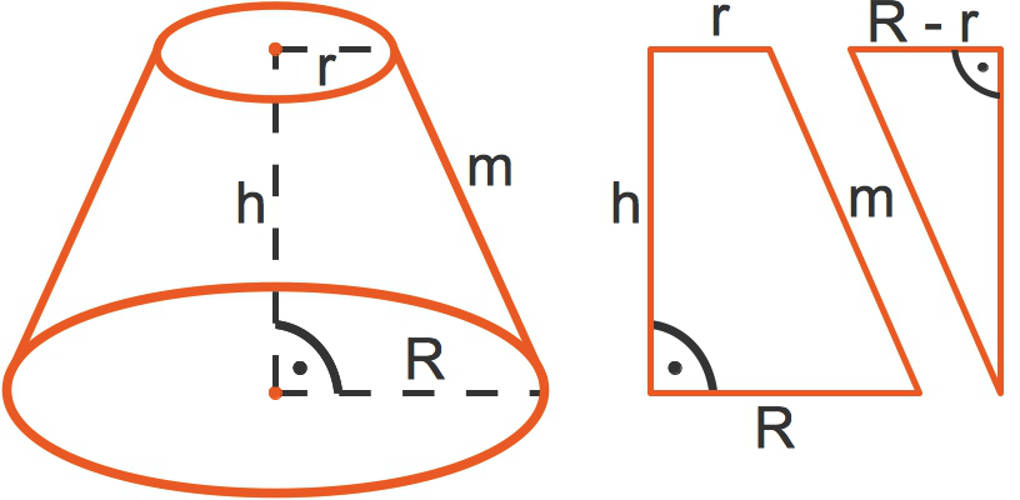
Auch hier kannst du mit dem Satz des Pythagoras die fehlende Größe berechnen:
$m=\sqrt{(R-r)^2+h^2}=\sqrt{(12,4~dm)^2+(45~dm)^2}\approx46,7~dm$.
Nun endlich kann die Mantelfläche berechnet werden:
$M\approx 3\pi\cdot (46,7~dm)\cdot (12,4~dm)\approx5457,7~dm^2$.
Fast fertig. Wenn du noch die Grundfläche $A_G\approx \pi\cdot (24,8~dm)^2=1932,2~dm^2$ addierst, erhältst du den gesuchten Materialaufwand: $5457,7~dm^2+1932,2~dm^2=7389,9~dm^2$.
Was ist eine Kugel?
Eine Kugel ist ein geometrischer Körper. Sie hat weder Ecken noch Kanten und nur eine Fläche.

Eine Kugel hat einen Mittelpunkt $M$ und einen Radius $r$. Jeder Punkt auf dem Kugelrand hat den gleichen Abstand $r$ zu dem Mittelpunkt. Der Durchmesser ist das Doppelte vom Radius: $d=2r$.
Kugeln sind dir bestimmt schon viele begegnet:

- Ein Globus ist ein Modell des Planeten Erde, auf dem wir leben.
- Eine Eiskugel ist, wie der Name schon verrät, auch eine Kugel.
- Spielst du gerne Fußball oder Tennis oder Minigolf oder Tischtennis? Diese Bälle haben alle die Form einer Kugel.
Berechnung der Oberfläche
Die Oberfläche einer Kugel lässt sich mit der Formel
$O=4\cdot\pi\cdot r^2$
berechnen. Dabei ist $\pi=3,1415...$ die sogenannte Kreiszahl.
Der Fußball
Ein Fußball hat einen Durchmesser von $22~cm$.
Der Fußballverein Glasbachtal möchte zum 75. Vereinsjubiläum für eine Tombola einen Fußball in den Vereinsfarben bestellen. Wie viel Material wird für den Ball benötigt?
Hier interessiert uns die Oberfläche des Balles. Außerdem benötigen wir den Radius für die Berechnung der Oberfläche. Du musst also erst einmal den Durchmesser $d=22$ durch $2$ teilen: $r=11~cm$.
Damit ist $O=4\cdot \pi\cdot(11~cm)^2=484\cdot\pi~cm^2\approx 1520,5~cm^2$.
Dies ist der gesuchte Materialaufwand.
Die Lampe
Camilla möchte sich eine Lampe aus Stoff basteln. Die Lampe hat die Form einer Kugel mit dem Radius $r=20~cm$.

Die benötigte Menge Stoff ist
$O=4\cdot \pi\cdot(20~cm)^2=1600\cdot \pi~cm^2\approx5026,5~cm^2$.
Sie hat leider nur genügend Geld für $3500~cm^2$. Wie groß kann die Lampe dann werden?
Camilla muss die Oberflächenformel umformen:
$O = 4 \cdot \pi \cdot r^2~~~ \Leftrightarrow~~~r=\sqrt{\frac{O}{4\cdot\pi}}$.
Nun kann sie die bekannten Größen in diese Formel einsetzen:
$r=\sqrt{\frac{3500~cm^2}{4\cdot\pi}}\approx16,7~cm$.
Durch die deutlich geringere Oberfläche wird die Lampe im Radius insgesamt gar nicht so viel kleiner. Woran kann das liegen?
Dies lässt sich dadurch begründen, dass der Radius quadriert wird.
- Zum Beispiel führt eine Halbierung des Radius’ zu einem Viertel der Fläche.
- Eine Verdoppelung des Radius’ führt zu der vierfachen Fläche.
Berechnung des Volumens
Das Volumen einer Kugel kannst du mit der folgenden Formel berechnen:
$V=\frac43\cdot\pi\cdot r^3$.
Die Eisdiele
In der Eisdiele „Lecker-Eis“ werden riesige Eiskugeln mit dem Radius $r=3,5~cm$ verkauft. Paul und Luke überlegen, welches Volumen die Eiskugeln haben.

Sie verwenden die Volumenformel:
$V=\frac43\cdot \pi\cdot(3,5~cm)^3=\frac{343}6\cdot\pi~cm^3\approx179,6~cm^3$.
Die Superkugel
Eine Superkugel Eis mit dem Radius $r=3,5~cm$ kostet $7,00~€$. Paul überlegt, ob dann eine Kugel Eis mit dem Radius $r=1,5~cm$ auch $3,00~€$ kostet, wenn der Preis einer Kugel Eis proportional zu dem Volumen ist.
Er rechnet das Volumen der kleineren Kugel aus:
$V=\frac43\cdot \pi\cdot(1,5~cm)^3=\frac{9}2\cdot\pi~cm^3\approx14,1~cm^3$.
Das ist weniger als ein Zehntel des Volumens der Superkugel. Eine Kugel Eis mit Radius $r=1,5~cm$ sollte
$\frac{14,1~cm^3}{179,6~cm^3}\cdot 7,00~€\approx0,55~€$
kosten.
Die richtige Eiskugel
Wie groß muss der Radius der Eiskugel sein, damit der Preis von $3,00~€$ gerechtfertigt ist? Auch hier wird wieder die proportionale Beziehung von Volumen und Preis verwendet:
$V=\frac{3,00~€}{7,00~€}\cdot 179,6~cm^3\approx77~cm^3$.
Nun kennt Paul das Volumen. Um den Radius zu berechnen, muss er die Volumenformel umstellen:
$r=\sqrt[3]{\frac{V}{\frac43\cdot\pi}}$.
Nun kann er das bekannte Volumen in diese Formel einsetzen:
$r=\sqrt[3]{\frac{77~cm^3}{\frac43\cdot\pi}}\approx 2,64~cm$.
Die Eiskugel, welche $3,00~€$ kosten sollte, hat den Radius $r=2,64~cm$.
Alle Videos und Lerntexte zum Thema
Videos und Lerntexte zum Thema
Volumen und Oberfläche von Pyramiden, Kegeln und Kugeln (9 Videos, 2 Lerntexte)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Volumen und Oberfläche von Pyramiden, Kegeln und Kugeln (9 Arbeitsblätter)
-
 Pyramide – Volumen und Oberfläche berechnen
PDF anzeigen
Pyramide – Volumen und Oberfläche berechnen
PDF anzeigen -
 Kegel – Volumen und Oberfläche
PDF anzeigen
Kegel – Volumen und Oberfläche
PDF anzeigen -
 Kugel – Volumen und Oberfläche
PDF anzeigen
Kugel – Volumen und Oberfläche
PDF anzeigen -
 Kegel: Volumen und Oberfläche – Übungen
PDF anzeigen
Kegel: Volumen und Oberfläche – Übungen
PDF anzeigen -
 Oberfläche und Volumen von Kegelstümpfen – Herleitung
PDF anzeigen
Oberfläche und Volumen von Kegelstümpfen – Herleitung
PDF anzeigen -
 Berechnungen am Kegelstumpf
PDF anzeigen
Berechnungen am Kegelstumpf
PDF anzeigen -
 Platonische Körper
PDF anzeigen
Platonische Körper
PDF anzeigen -
 Oberfläche und Mantelfläche von Kegeln
PDF anzeigen
Oberfläche und Mantelfläche von Kegeln
PDF anzeigen -
 Oberfläche und Mantelfläche von Kegeln – Übungen
PDF anzeigen
Oberfläche und Mantelfläche von Kegeln – Übungen
PDF anzeigen
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung






















