Ableitung – Erklärung

in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
Grundlagen zum Thema Ableitung – Erklärung
Nach dem Schauen dieses Videos wirst du wissen, was eine Ableitung ist und wozu man sie gebrauchen kann.

Zunächst lernst du, was die Ableitung mit der Steigung einer Funktion zu tun hat. Anschließend schauen wir uns an, wozu man eine Ableitung benötigt. Abschließend lernst du eine erste Regel, mit der die Ableitung bestimmt werden kann.
Das Video beinhaltet Schlüsselbegriffe, Bezeichnungen und Fachbegriffe wie Steigung, Ableitung, Tangente, Steigungsdreieck, lokale und momentane Änderungsrate.

Bevor du dieses Video schaust, solltest du bereits wissen, wie man das Steigungsdreieck bei linearen Funktionen verwendet und die Idee des Differenzen- und des Differentialquotienten kennen.

Nach diesem Video wirst du darauf vorbereitet sein, weitere Ableitungsregeln kennenzulernen.
Transkript Ableitung – Erklärung
Täglich liest man Schlagzeilen wie diese: Die weltweiten Gletscher schrumpfen mit wachsendem Tempo. Die Inzidenz steigt langsamer. Die Talfahrt im Dax geht leicht gebremst weiter. Der Meeresspiegel steigt immer schneller. Um zu erkennen, ob das alles schlechte Nachrichten sind, brauchen wir grundlegendes Wissen über „die Ableitung“. Schauen wir uns das letzte Diagramm nochmal genauer an. Wie ist das jetzt mit der Steigung? Und wie kann man die Steigung bei so einer krummen Funktion überhaupt messen? Nehmen wir uns mal eine Funktion her. Ähnlich wie in dem Diagramm, ist sie ziemlich krumm und gebogen. Wenn wir aber trotzdem etwas über die Steigung – an zum Beispiel diesem Punkt – herausfinden wollen, brauchen wir ein Hilfsmittel. Lass uns hier mal eine Tangente anlegen. Nochmal kurz zur Erinnerung: Tangenten kennen wir schon. Das waren die Geraden am Kreis, die den Kreis in nur einem Punkt berühren. Diese Tangente berührt die Funktion nur in diesem einen Punkt. Okay, vielleicht schneidet die Tangente die Funktion weiter links, aber darum geht es hier nicht - wir betrachten dabei immer nur einen lokalen Ausschnitt der Funktion. Bei der Tangente können wir nun, wie bei den linearen Funktionen, ein Steigungsdreieck einzeichnen, um den Anstieg zu ermitteln. Dabei ist es egal, wo und wie groß wir das Steigungsdreieck an die Tangente legen, da das Verhältnis von Delta y zu Delta x immer gleich bleibt. Da die Tangente immer perfekt am Funktionsgraphen anliegt, gibt sie an, wie groß der Anstieg an exakt dieser Stelle ist. Und genau das ist schon die Ableitung an dieser Stelle „x null“. Die Ableitung gibt die momentane Steigung, also die Tangentensteigung an einer bestimmten Stelle an. Aber die Steigung ist bei diesem Funktionsgraphen natürlich nicht immer gleich. Im Punkt C ist die Funktion schon wesentlich steiler. An dieser Stelle ist die Steigung dagegen negativ, denn auch die anliegende Tangente fällt. Und im Punkt A positiv. Wir schauen also immer, ob die Funktionswerte von links nach rechts zu- oder abnehmen. Wenn wir nun die Steigung an allen Stellen bestimmen, und sie in ein Koordinatensystem eintragen, erhalten wir eine Funktion, die uns an jeder Stelle direkt den Anstieg der Funktion f anzeigt. Das ist die Ableitungsfunktion der Funktion f. Die Ableitung ist also eine weitere Funktion, die jeder Stelle x von f den Anstieg an dieser Stelle zuordnet. Diese Funktion wird „f Strich“ genannt. f, weil sie von der Funktion f abgeleitet wurde, und mit dem Strich können wir sie von der Ausgangsfunktion unterscheiden.
Wenn wir die beiden Funktionen jetzt vergleichen, ist ein weiterer Zusammenhang erkennbar. In den Bereichen, in denen die Funktion f steigt, sind die Funktionswerte der Ableitung positiv. Wenn f dagegen fällt, verläuft die Ableitungsfunktion im negativen Bereich. Und wenn die Funktion weder steigt noch fällt, wie zum Beispiel hier oder hier, dann ist der Funktionswert der Ableitung genau null. Die Ableitung beschreibt also, in welche Richtung sich die Funktion f gerade weiterbewegt, ob sie steigt oder fällt. Das ist ja alles schön und gut, aber wofür braucht man eine Ableitung überhaupt? Zum Beispiel, wenn eine Funktion den zurückgelegten Weg angibt, kann man mit der Ableitung die Geschwindigkeit ermitteln. Die Steigung an einer bestimmten Stelle ist dann die Geschwindigkeit zu diesem Zeitpunkt. Bei dem Gewicht einer Babykatze gibt die Ableitung die Gewichtszu- oder abnahme an. Und bei der Erlös- oder Kostenfunktion die zusätzlichen Erlöse oder Kosten pro weiteres produziertes Stück. Ganz schön vielfältig, diese Ableitungen. Doch wie kommt man eigentlich auf die Ableitungsfunktion, wenn man gerade eine braucht? Nun, da gibt es ein paar Regeln. Vielleicht erkennst du ja die erste, wenn du einen ganz scharfen Blick auf diese Tabelle wirfst. Genau, der Exponent der Ausgangsfunktion, wird vor das x gezogen, und der Exponent wird um eins kleiner gemacht. Allgemein kann das so aufgeschrieben werden. Der Exponent n, wird bei der Ableitung nach vorne geholt, und oben um eins verringert. Zum Ableiten gibt es noch einige weitere Regeln, aber wir fassen das Wichtigste erstmal zusammen. Die Ableitung einer Funktion ist wieder eine Funktion, an der wir die Steigung der Ausgangsfunktion für jede Stelle x direkt ablesen können. Die Ableitung von f an einer Stelle „x null“ ist somit die Steigung des Graphen von f an der Stelle „x null“, beziehungsweise die Steigung der Tangente, die an der Stelle „x null“ an dem Graphen anliegt. Sie wird auch lokale oder momentane Änderungsrate an der Stelle „x null“ genannt. Aber eigentlich reicht es, wenn man sich merkt, dass die Ableitung beschreibt, in welche Richtung sich die Funktion f gerade weiterbewegt. Auf jeden Fall hilft uns die Ableitung dabei, Änderungsraten genauer unter die Lupe zu nehmen um endlich den Durchblick zu haben.
Ableitung – Erklärung Übung
-
Beschreibe die Bedeutung der Ableitung an der Stelle $x_0$.
TippsDie Ableitung $f^\prime(x)$ ist eine Funktion, die den Anstieg der Funktion $f(x)$ beschreibt.
Die mittlere Änderungsrate ist die Steigung einer Graden durch zwei Punkte.
LösungDie Ableitung $f^\prime(x)$ einer Funktion $f(x)$ ist selbst eine Funktion, welche den Anstieg bzw. die Steigung von $f(x)$ beschreibt. Die Steigung einer Funktion in einem bestimmten Punkt wird auch als momentane oder lokale Änderungsrate bezeichnet.
Wenn wir eine Gerade so einzeichnen, dass sie den Funktionsgraphen in einem Punkt berührt (Tangente), so hat sie stets die Steigung der Funktion im Berührungspunkt.Korrekte Aussagen:
- $f^\prime(x_0)$ beschreibt die momentane Änderungsrate von $f(x)$ an der Stelle $x_0$.
- $f^\prime(x_0)$ beschreibt die Steigung einer Tangenten an dem Graphen von $f(x)$ an der Stelle $x_0$.
- $f^\prime(x_0)$ beschreibt die Steigung des Graphen von $f(x)$ an der Stelle $x_0$.
- $f^\prime(x_0)$ beschreibt die mittlere Änderungsrate von $f(x)$ in einem Intervall um $x_0$.
-
Gib an, was durch die Ableitung der Größen beschrieben wird.
TippsDie Ableitung beschreibt stets eine Änderungsrate.
Beispiel:
$f: x \mapsto$ Geschwindigkeit
$f^\prime: x \mapsto$ Beschleunigung
Die Beschleunigung gibt an, wie sich die Geschwindigkeit ändert.
LösungDie Ableitung einer Funktion beschreibt ihre Änderungsrate. Wenn die Funktion $f(x)$ für eine Größe steht, dann beschreibt die Ableitung $f^\prime(x)$ die Änderung dieser Größe.
Beispiel 1:
$f: x \mapsto$ zurückgelegter Weg
Die Ableitung beschreibt, wie sich der zurückgelegte Weg in Abhängigkeit von der Zeit verändert. Die Änderung des Weges in Abhängigkeit von der Zeit entspricht der Geschwindigkeit. Dies erkennen wir auch an den Einheiten, wie z.B. $\text{km}$ für den Weg und $\frac{\text{km}}{\text{h}}$, also Weg pro Zeit, für die Geschwindigkeit.
$\Rightarrow f^\prime: x \mapsto$ GeschwindigkeitBeispiel 2:
$f: x \mapsto$ Gewicht einer Babykatze
Die Ableitung beschreibt, wie sich das Gewicht verändert, also die Gewichtsänderung.
$\Rightarrow f^\prime: x \mapsto$ GewichtsänderungBeispiel 3:
$f: x \mapsto$ Erlös
Die Ableitung beschreibt, wie sich der Erlös abhängig von der Stückzahl verändert.
$\Rightarrow f^\prime: x \mapsto$ zusätzlicher Erlös pro StückBeispiel 4:
$f: x \mapsto$ Kosten
Die Ableitung beschreibt, wie sich die Kosten abhängig von der Stückzahl verändern.
$\Rightarrow f^\prime: x \mapsto$ zusätzliche Kosten pro Stück -
Entscheide, welcher Graph die Ableitung der Funktion darstellt.
TippsIn den Bereichen, in denen $f(x)$ steigt gilt: $f^\prime(x) \gt 0$. Dort wo $f(x)$ fällt, ist die Ableitung negativ, also: $f^\prime(x) \lt 0$.
Beispiel:
LösungDa die Ableitung einer Funktion stets die Steigung des zugehörigen Funktionsgraphen beschreibt, bestehen die folgenden Zusammenhänge:
- Graph von $f(x)$ steigt $\Rightarrow f^\prime(x) \gt 0$
- Graph von $f(x)$ fällt $\Rightarrow f^\prime(x) \lt 0$
- Graph von $f(x)$ steigt oder fällt nicht $\Rightarrow f^\prime(x) = 0$
Beispiel 1: (vgl. Abbildung)
Da der Funktionsgraph mit zunehmenden $x$-Werten erst steigt, dann fällt und schließlich wieder fällt, muss der Graph der Ableitung zunächst oberhalb, dann unterhalb und schließlich wieder oberhalb der $x$-Achse verlaufen, damit die Ableitung zunächst positive, dann negative und schließlich wieder positive Werte annimmt. Die Nullstellen der Ableitung befinden sich bei den $x$-Werten, an denen der Funktionsgraph weder steigt noch fällt.Beispiel 2:
Der Funktionsgraph fällt zunächst, steigt dann und fällt schließlich wieder. Der Graph der Ableitung muss daher zunächst unterhalb, dann oberhalb und schließlich wieder unterhalb der $x$-Achse verlaufen. Er hat die Form einer nach unten geöffneten Parabel. Die Nullstellen liegen bei den $x$-Werten, an denen der Graph von $f(x)$ waagrechte Tangenten hat.Beispiel 3:
Der Funktionsgraph fällt für $x \lt 1$ und steigt für $x \gt 1$. Für $x = 1$ hat er eine waagrechte Tangente. Der Graph der Ableitung muss daher bei $x = 1$ eine Nullstelle haben. Außerdem muss er links davon unterhalb und rechts davon oberhalb der $x$-Achse verlaufen. Der Graph der Ableitung ist eine steigende Gerade.Beispiel 4:
Der Funktionsgraph steigt für $x \lt -1$ und fällt für $x \gt -1$. Für $x = -1$ hat er eine waagrechte Tangente. Der Graph der Ableitung muss daher bei $x = -1$ eine Nullstelle haben. Außerdem muss er links davon oberhalb und rechts davon unterhalb der $x$-Achse verlaufen. Der Graph der Ableitung ist eine fallende Gerade. -
Formuliere eine Aussage über die Ableitung der dargestellten Funktion.
TippsDie Ableitung beschreibt die Tangentensteigung einer Funktion.
Überlege, ob die Tangente an dem Funktionsgraph steigt oder fällt.
An den Nullstellen der Ableitung hat der Graph der Funktion eine waagrechte Tangente.
LösungDie Ableitung ist eine Funktion, welche die Steigung eines Funktionsgraphen in jedem Punkt beschreibt. Graphisch können wir die Ableitung in einem Punkt bestimmen, indem wir eine Tangente an den Graphen zeichnen. Dabei gilt:
- die Tangente in $x_0$ steigt $\Rightarrow f^\prime(x_0) \gt 0$
- die Tangente in $x_0$ fällt $\Rightarrow f^\prime(x_0) \lt 0$
- die Tangente in $x_0$ ist waagrecht $\Rightarrow f^\prime(x_0) = 0$
Für die Ableitungen der dargestellten Funktionsgraphen gilt:
Graph 1:
Die Tangenten an den Graphen bei $x = -1$ und $x = 1$ fallen beide.
$\Rightarrow f^\prime(-1) \lt 0$ und $f^\prime(1) \lt 0$Graph 2:
Der Graph hat bei $x = 3$ eine waagrechte Tangente.
$\Rightarrow f^\prime(3) = 0$Graph 3:
Alle Tangenten an den Graphen steigen.
$\Rightarrow f^\prime(x) \gt 0$ für $x \in \mathbb{R}$Graph 4:
Der Graph hat drei waagrechte Tangenten bei $x_1 \approx -2,8$; $x_2 = 0$ und $x_3 \approx 2,8$.
$\Rightarrow f^\prime(x)$ hat drei Nullstellen.Graph 5:
Die Tangente fällt bei $x = -1$, die Tangente steigt bei $x = 1$.
$\Rightarrow f^\prime(-1) \lt 0$ und $f^\prime(1) \gt 0$ -
Vervollständige die Tabelle mit den Ableitungen der Funktionen.
TippsDie Potenzregel für Ableitungen lautet:
$f(x)=x^n \Rightarrow f^\prime(x) = n \cdot x^{n-1}$
Für $x$ kann man auch $x^1$ schreiben.
Beispiel:
$f(x) = x^8 \Rightarrow f^\prime(x) = 8x^7$
LösungDie Ableitung einer Potenz von $x$ können wir nach der folgenden Regel bilden:
$f(x)=x^n \Rightarrow f^\prime(x) = n \cdot x^{n-1}$
Wir multiplizieren also mit dem Exponenten und verringern diesen um $1$.Diese Ableitungsregel können wir auch aus der Tabelle ablesen:
$\begin{array}{c|c} f(x) & f^\prime(x) \\ \hline x & 1 \\ x^2 & 2x \\ x^3 & 3x^2 \\ x^4 & 4x^3 \\ x^5 & 5x^4 \end{array}$
Hinweis:
Für $f(x)=x=x^1$ ist die Ableitung laut Regel: $f^\prime(x) = 1 \cdot x^{1-1} = 1 \cdot x^0 = 1 \cdot 1 = 1$ -
Bestimme die Gleichung der Tangente an den Funktionsgraphen.
TippsBestimme zunächst die Koordinaten des Berührpunktes $P(x_0 \vert f(x_0))$.
Eine Geradengleichung hat allgemein die Form:
$y = m \cdot x + b$
Dabei steht $m$ für die Steigung und $b$ für den $y$-Achsenabschnitt.
Für eine Tangente gilt:
$m = f^\prime(x_0)$
LösungEine Tangente ist eine Gerade, die den Graphen der Funktion in einem Punkt berührt. Die allgemeine Form einer Geradengleichung lautet:
$y = m \cdot x + b$
Dabei ist $m$ die Steigung und $b$ der $y$-Achsenabschnitt.Da die Ableitung einer Funktion die Tangentensteigung in jedem Punkt der Funktion angibt, bestimmen wir zunächst die Ableitung von $f(x) = x^7$.
Wir kennen die Ableitungsregel $f(x) = x^n \Rightarrow f^\prime(x) = n \cdot x^{n-1}$ (Potenzregel). Hier ist $n = 7$, es gilt:
$f^\prime(x) = 7x^6$Damit gilt für die Steigung der Tangente in $x_0 = 1$:
$m = f^\prime(1) = 7 \cdot 1^6 = 7 \cdot 1 = 7$Wir setzen diesen Wert in die allgemeine Form der Geradengleichung ein:
$y = 7\cdot x + b$Da die Tangente den Funktionsgraphen bei $x_0 = 1$ berührt, muss sie den Punkt $P(x_0 \vert f(x_0))$ mit der Funktion gemeinsam haben. Hier gilt $x_0 = 1$ und $f(x_0) = f(1) = 1^7 = 1$. Wir setzen $P(1 \vert 1)$ in die Gleichung der Geraden ein:
$\begin{array}{rcll} 1 & = & 7 \cdot 1 + b & \\ 1 & = & 7 + b & \vert -7 \\ -6 & = & b & \end{array}$Damit lautet die Gleichung der Tangente:
$y = 7 \cdot x - 6$
9.369
sofaheld-Level
6.600
vorgefertigte
Vokabeln
8.220
Lernvideos
38.687
Übungen
33.508
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Klassenstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Quadratische Gleichungen – Übungen
- Flächeninhalt




 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?


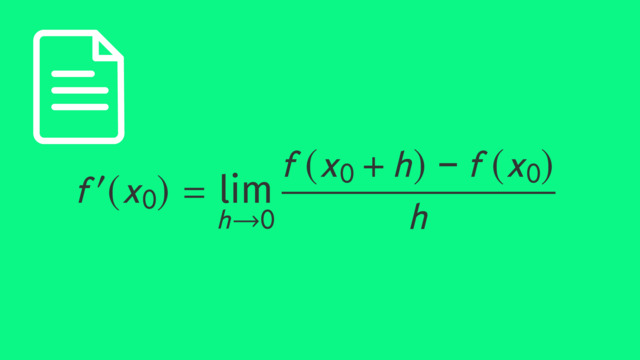














Gutes Video, nur eine kurze Zusammenfassung als Text dazu wäre noch mega gewesen. :D