Scharen von Exponentialfunktionen – Kurvendiskussion (1)


in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
Grundlagen zum Thema Scharen von Exponentialfunktionen – Kurvendiskussion (1)
Exponentialfunktionen sind Dir bekannt? Du kennst die Ableitung der Exponentialfunktion und deren Eigenschaften? Dann können wir uns ja eine Kurvendiskussion anschauen, in welcher eine Exponentialfunktion mit Parameter vorkommt. Dabei kannst Du auch sehen, wie sich der Verlauf des Funktionsgraphen in Abhängigkeit des Parameter verändert. Ich würde mich über Fragen und Anregungen freuen. Ich wünsche Dir viel Spaß mit diesem Video, dein Frank.
Transkript Scharen von Exponentialfunktionen – Kurvendiskussion (1)
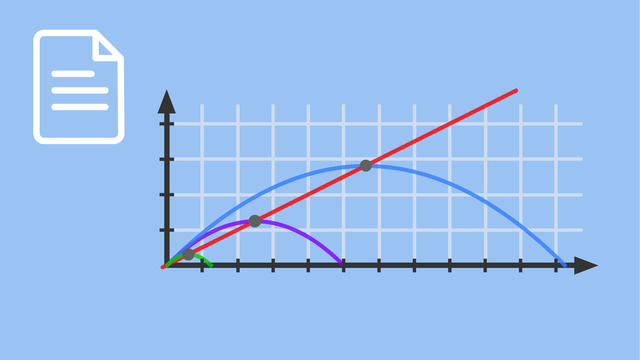
Hallo, mein Name ist Frank und ich werde in diesem Video eine Kurvendiskussion anhand einer Exponentialfunktion erklären. Die Punkte der Kurvendiskussion sind hier rechts angeschrieben. Dafür betrachte ich eine Funktion fa(x)=ex×(x + a) Das ist eine Kurvenschar mit den Scharparametern: a. Zu den Ableitungen: Die erste Ableitung führe ich jetzt hier mal vor: fa'(x)= ex×(x+a) + ex×1. Da kann ich jetzt ex ausklammern und erhalte: ex×(x + a + 1). Das schreibe ich nochmal hier auf: fa'(x)=ex×(x + a + 1) Ebenso erhalte ich die zweite Ableitung: fa'‘(x)=ex×(x + a + 3) und die dritte Ableitung: fa'‘‘(x)=ex×(x + a + 3). Dann komme ich im Folgenden zu den Achsenschnittpunkten. Da wären zuerst die Nullstellen: fa(x)=0 . Ich übernehme die Funktion: ex×(x + a)=0. Der Faktor wird ex wird nie null, also erhalte ich die Nullstelle: x = -a. Also Nullstelle N(-a|0). Der y-Achsenschnittpunkt, den bekommen wir dadurch, dass wir für x=0 einsetzen: fa(0)=e0×(0 + a) = a. Der Y-Achsenschnittpunkt Y(0|a). Nun komme ich zu den Extrema. Für die Extrema untersuche ich zuerst das notwendige Kriterium: (n) fa'(xE)=0 Ich übernehme auch hier die erste Ableitung: exE×(xE + a + 1). Wieder e hoch wird nicht null, also kann nur der andere Term null werden. Ich erhalte: xE = -a-1 Ob das jetzt ein Extrem ist, kommen wir, kommen wir durch das hinreichende Kriterium, setzte also –a-1 in die nächste Ableitung ein: (h) fa'‘(-a - 1)=e-a - 1 > 0 .Das ist ungleich null, insbesondere größer null. Die y-Koordinate erhalten wir durch einsetzen der Funktion. Also haben wir einen Tiefpunkt: TP(-a - 1|-e-a - 1) Damit haben wir den Tiefpunkt und werden uns im Folgenden die Wendepunkte anschauen. Nachdem wir die ersten Punkte “Ableitungen”, “Achsenschnittpunkte” und “Extrema” schon fertig haben, schauen wir uns jetzt die Wendepunkte an. Bei den Wendepunkten muss notwendigerweise gelten, die zweite Ableitung an der Stelle xw ist gleich null: (n) fa'‘(xw) = 0, Ich übernehme die zweite Ableitung: exw×(xw + a + 2) = 0.Wider exw wird nie null, das heißt: xw = -a - 2. Nun brauche ich noch das hinreichende Kriterium, um zu sehen, dass es wirklich ein Wendepunkt ist. Ich setze also -a - 2 in die dritte Ableitung ein. Da kommt also raus: (h) fa’’’(-a-2)=e-a - 2 und wenn ich hier x = -a - 2 einsetze bekomme ich 1. Also das ist ungleich 0. Wir haben also einen Wendepunkt gefunden. Die y-Koordinate bekommen wir in dem wir das -a - 2 in der Funktionsvorschrift einsetzen: WP (-a - 2/-2e-a - 2) Damit haben wir auch die Wendepunkte. Und jetzt schaue ich mir das Grenzwertverhalten an. Einmal betrachte ich den Grenzwert: limx->∞ fa(x) und einmal limx->-∞ fa(x). Wenn ich für x in der Funktion immer größere Werte einsetze, geht beides gegen unendlich, ich bekomme also insgesamt unendlich: limx->∞ fa(x)=“∞“ und wenn ich immer größere negative Werte einsetze geht die Funktion gegen null: limx->-∞ fa(x) = 0. Nachdem ich auch die Grenzwerte fertig habe, komme ich im Folgenden zur Skizze. So, nachdem wir diese Punkte alle betrachtet haben, komme ich sozusagen als krönender Abschluss einer Kurvendiskussion. Hier haben wir dann noch den besonderen Fall einer Kurvenschar, das heißt ich werde jetzt den Verlauf der Funktion für verschiedene Scharparameter a zeichnen. Dabei beginne ich bei a = null. Und du kannst dir der Einfachheit halber immer die Nullstellen und den y-Achsenabschnitt anschauen. Für a = null stimmen die beiden überein. Das heißt die liegen im Koordinatenursprung und die Funktion hat diesen Verlauf. Was du hier schon sehen kannst, ist das Grenzwertverhalten. limx->-∞ fa(x) = 0. Also hier. limx->∞ fa(x)=“∞“, also hier. Nun schaue ich mir den Parameter a = 1 an. Wäre die Nullstelle (-1|0), also da. Und der y-Achsenabschnitt (0|1) also da. Der Verlauf der Funktion ist dann so. Zu guter Letzt schaue ich mir noch einen negativen Parameter an, also a = -1. Die Nullstelle wäre (1|0) und der y-Achsenabschnitt (0|-1). Das ist auch gleichzeitig der Tiefpunkt dieser Funktion. Wir haben also diesen Verlauf. Ich fasse noch einmal kurz zusammen. In diesem Video habe ich eine Kurvendiskussion mit einer Exponentialfunktion durchgeführt. Die einzelnen Punkte der Kurvendiskussion siehst du hier rechts. Und habe insbesondere, da wir hier eine Kurvenschar haben, den Verlauf in Abhängigkeit des Parameters hier nochmal. Ich hoffe, du konntest alles gut verstehen. Danke dir für deine Aufmerksamkeit und bis zum nächsten Mal. Dein Frank.
Scharen von Exponentialfunktionen – Kurvendiskussion (1) Übung
-
Beschreibe das allgemeine Vorgehen bei einer Kurvendiskussion.
TippsEs müssen dreimal Nullstellen berechnet werden:
- die der Funktion,
- die der 1. Ableitung, für die Extrema, und
- die der 2. Ableitung, für die Wendepunkte.
Wenn die 1. Ableitung $0$ ist, heißt dies nur, dass eine waagerechte Tangente an der entsprechenden Stelle vorliegt. Es muss noch kein Extremum sein.
Auch ein Sattelpunkt hat eine waagerechte Tangente.
Beachte, dass die Kriterien bei den Extrema und Wendepunkten sehr ähnlich aussehen.
LösungBei einer Kurvendiskussion müssen die folgenden Punkte bearbeitet werden. Die Reihenfolge kann dabei verändert werden, wobei die Ableitungen für die Extrema und Wendepunkte benötigt werden.
- Zunächst werden die ersten drei Ableitungen benötigt.
- Der Graph der Funktion kann die y-Achse in einem Punkt schneiden, dem y-Achsenschnittpunkt. Diesen erhält man, indem man $x=0$ in der Funktionsgleichung einsetzt. Es kann mehrere Schnittpunkte mit der x-Achse geben, die Nullstellen. Dafür muss die Gleichung $f(x)=0$ gelöst werden.
- Extrema: Es sind zwei Kriterien zu untersuchen: (n) $f'(x_E)=0$ und (h) $f''(x_E)\neq0$. Dabei steht „(n)“ für notwendig und „(h)“ für hinreichend.
- Wendepunkte: Es sind zwei Kriterien zu untersuchen: (n) $f''(x_W)=0$ und (h) $f'''(x_W)\neq0$.
- Die Grenzwerte der Funktion für $x \to ±\infty$ werden berechnet.
- Zu guter Letzt kann der Graph der Funktion mit Hilfe der bisherigen Ergebnisse und gegebenenfalls ergänzend einer Wertetabelle skizziert werden.
-
Gib den y-Achsenschnittpunkt, die Nullstelle, den Extrem- und den Grenzwert für $x\to \infty$ der Funktion an.
TippsDer y-Achsenschnittpunkt liegt auf der y-Achse, also ist die x-Koordinate dieses Punktes $0$.
Die Nullstelle liegt auf der x-Achse, also ist die y-Koordinate dieses Punktes $0$.
Für Extrema gilt
- (notwendig) $f'(x_E)=0$ und
- (hinreichend) $f''(x_E)\neq 0$.
Für Wendepunkte gilt
- (notwendig) $f''(x_W)=0$ und
- (hinreichend) $f'''(x_W)\neq 0$.
LösungWir wollen die Achsenschnittpunkte, die Extrema und das Grenzverhalten der Funktionsschar $f_a(x)=e^x\cdot (x+a)$ berechnen.
- y-Achsenschnittpunkt: Es muss $x=0$ in der Funktionsgleichung eingesetzt werden: $y=e^0(0+a)=a$, also $Y(0|a)$.
- Nullstelle: Es muss die Gleichung $f_a(x)=0$ gelöst werden.
Also $N(-a|0)$.
- Extrema: Der Ansatz lautet (n) $f'(x_E)=0$ und (h) $f''(x_E)\neq0$.
Einsetzen von $x_E=-a-1$ in
- $f''_a(-a-1)=e^{-a-1}>0$
- führt zu $TP(-a-1|-e^{-a-1})$. Die y-Koordinate erhält man durch Einsetzen von $-a-1$ in der Funktionsgleichung $f_a(x)$.
- Der Grenzwert kann zum Beispiel durch Testeinsetzen berechnet werden. Das heißt man setzt immer größere positive $x$ in der Funktionsgleichung ein und stellt eine Vermutung über den Grenzwert (zum Beispiel für $a=1$, der Grenzwert ist für alle $a$ gleich) an:
Es liegt der uneigentliche Grenzwert, „$+\infty$“, vor.
-
Bestimme die ersten drei Ableitungen der Funktion.
TippsZur Ableitung eines Produktes zweier Funktionen wird die Produktregel angewendet:
$(f(x)\cdot g(x))'=f'(x)\cdot g(x)+f(x)\cdot g'(x)$
oder in der Kurzschreibweise $(u\cdot v)'=u'\cdot v+u \cdot v'$.
Für die Exponentialfunktion $e^x$ gilt $(e^x)'=e^x$.
Da beim Anwenden der Produktregel zum Beispiel auf die Funktion $f(x)=x e^x$ der zweite Faktor sowohl als Funktion als auch als Ableitung erhalten bleibt, kann dieser ausgeklammert werden:
$\begin{align*} (x e^x)'&=1 e^x+xe^x\\ &=(1+x)e^x\\ &=(x+1)e^x. \end{align*}$
Ebenso kann in der 2. und 3. Ableitung der Faktor $e^x$ ausgeklammert werden.
Die 2. Ableitung ist die Ableitung der 1. Ableitung.
Die 3. Ableitung ist die Ableitung der 2. Ableitung.
LösungZur Berechnung der 1. Ableitung wird
- zum einen die Produktregel $(u\cdot v)'=u'\cdot v+u \cdot v'$ und
- zum anderen $(e^x)'=e^x$ sowie $(x^2)'=2x$ verwendet.
Dabei wurde der Faktor $e^x$ ausgeklammert.
Ebenso können die 2. und 3. Ableitung berechnet werden.
$\begin{align*} f''(x)&=(2x+2)e^x+(x^2+2x)e^x\\ &=(2x+2+x^2+2x)e^x\\ &=(x^2+4x+2)e^x. \end{align*}$
$\begin{align*} f'''(x)&=(2x+4)e^x+(x^2+4x+2)e^x\\ &=(2x+4+x^2+4x+2)e^x\\ &=(x^2+6x+6)e^x. \end{align*}$
-
Ermittle die Schnittpunkte mit der x-Achse und die Extrem- und Wendepunkte der Funktion.
TippsDie ersten drei Ableitungen sind:
$\begin{align*} f'(x)&=(x^2+2x)e^x\\ f''(x)&=(x^2+4x+2)e^x \\ f'''(x)&=(x^2+6x+6)e^x \end{align*}$
Für Extrema müssen die folgenden Punkte bearbeitet werden
- (n) $f'(x_E)=0$
- (h) $f''(x_E)\neq 0$.
- Für $f''(x_E)>0$ haben wir einen Tiefpunkt und für $f''(x_E)<0$ einen Hochpunkt.
- Angabe des Extrempunktes $E(x_E|f(x_E))$.
Für Wendepunkte müssen die folgenden Punkte bearbeitet werden
- (n) $f''(x_W)=0$
- (h) $f'''(x_W)\neq 0$.
- Angabe des Wendepunktes $WP(x_W|f(x_W))$.
Es gilt $e^{-2}\approx 0,13533 \approx 0,14$ und $\sqrt{2}\approx 1,41421 \approx 1,41$.
LösungDie ersten drei Ableitungen sind:
$\begin{align*} f'(x)&=(x^2+2x)e^x\\ f''(x)&=(x^2+4x+2)e^x \\ f'''(x)&=(x^2+6x+6)e^x \end{align*}$
Zunächst werden die Nullstellen berechnet. Es muss gelten
$\begin{align*} &&f(x)&=0\\ &\Leftrightarrow&x^2e^x&=0 &|&~e^x\neq 0\\ &\Leftrightarrow&x^2&=0 &|&~\sqrt{}\\ &\Leftrightarrow&x&=0. &\end{align*}$
Die Nullstelle ist $x=0$ und somit ist der Schnittpunkt mit der x-Achse $N(0|0)$.
Sowohl für die Extrema als auch für Wendepunkte müssen jeweils ein notwendiges und ein hinreichendes Kriterium untersucht werden:
- Extrema: Der Ansatz lautet (n) $f'(x_E)=0$ und (h) $f''(x_E)\neq0$.
Jede dieser beiden x-Koordinaten muss in die 1. Ableitung eingesetzt werden:
$\mathbf{x_{E1}=0}$: $f''(0)=2e^0=2>0$. Es liegt also ein Tiefpunkt vor. Die y-Koordinate ist $0$. Also ist $TP(0|0)$ ein Tiefpunkt.
$\mathbf{x_{E2}=-2}$: $f''(-2)=((-2)^2+2 4\cdot(-2)+2)e^{-2}=-2e^{-2}<0$. Es liegt also ein Hochpunkt vor. Die y-Koordinate ist $y=(-2)^2e^{-2}≈0,54$. Also ist $HP(-2|0,54)$ ein Hochpunkt.
- Wendepunkte: Der Ansatz lautet (n) $f''(x_W)=0$ und (h) $f'''(x_W)\neq0$.
Jede dieser beiden x-Koordinaten muss in die 3. Ableitung eingesetzt werden:
- $\mathbf{x_{W1}=-0,59}$: $f'''(-0,59)≈1,56\neq0$. Es liegt also ein Wendepunkt vor. Die y-Koordinate ergibt sich durch Einsetzen von $x=-0,59$ in der Funktionsgleichung. Der erste Wendepunkt ist $WP_1(-0,59|0,19)$.
- $\mathbf{x_{W2}=-3,41}$: $f'''(-3,41)≈-0,09\neq0$. Auch hier liegt also ein Wendepunkt vor. Die y-Koordinate ergibt sich wieder durch Einsetzen von $x=-3,41$ in der Funktionsgleichung. Der zweite Wendepunkt ist $WP_2(-3,41|0,38)$.
-
Bestimme den Wendepunkt der Funktion.
Tipps„notwendiges“ Kriterium $f''(x_W)=0$ für Wendepunkte bedeutet,
- dass, sofern dieses Kriterium nicht erfüllt ist, keine Wendepunkte vorhanden sind.
- wenn das Kriterium erfüllt ist, muss noch das hinreichende Kriterium $f'''(x_W)\neq 0$ untersucht werden.
Das notwendige Kriterium ist immer das Lösen einer Gleichung (hier $f''(x)=0$); das hinreichende das Einsetzen der Lösung(en) dieser Gleichung in die 3. Ableitung.
Um den Wendepunkt anzugeben, muss noch zu der x-Koordinate die y-Koordinate durch Einsetzen in der Funktionsgleichung berechnet werden.
LösungWendepunkte müssen die notwendige Bedingung $f''(x_W)=0$ und die hinreichende Bedingung $f'''(x_W)\neq0$ erfüllen. Wir berechnen:
$\begin{align*} &&f''_a(x_W)&=0\\ &\Leftrightarrow&e^{x_W}(x_W+a+2)&=0 &|&~e^{x_W}\neq 0\\ &\Leftrightarrow&x_W+a+2&=0 &|&~-a-2\\ &\Leftrightarrow&x_W&=-a-2. \end{align*}$
Einsetzen von $x_W=-a-2$ in $f'''_a(-a-2)=e^{-a-2}\neq0$ ergibt, dass auch die notwendige Bedingung erfüllt ist.
Die y-Koordinate erhält man durch Einsetzen von $-a-2$ in die Funktionsgleichung $f_a(x)$. Dies führt zum Wendepunkt $WP(-a-2|-2e^{-a-2})$.
-
Entscheide, welche Funktionsgleichung zu dem Graphen gehört.
TippsDer y-Achsenschnittpunkt liegt auf der y-Achse, also ist $x=0$.
Für die Schnittpunkte mit der x-Achse gilt $y=0$.
Für Extrema müssen die folgenden Punkte bearbeitet werden
- (n) $f'(x_E)=0$
- (h) $f''(x_E)\neq 0$.
- Bei Tiefpunkten gilt $f''(x_E)>0$ und bei Hochpunkten $f''(x_E)<0$.
- Angabe des Extrempuntkes $E(x_E|f(x_E))$.
Mit Hilfe der Achsenschnittpunkte kannst du aus den fünf angegebenen Funktionen die richtige Funktion eindeutig auswählen.
LösungDer rote Funktionsgraph besitzt den y-Achsenschnittpunkt $Y(0|3)$ und den x-Achsenschnittpunkt $N(-1,5|0)$. Mit Hilfe der Achsenschnittpunkte kannst du aus den fünf angegebenen Funktionen die richtige Funktion eindeutig auswählen: Die zugehörige Funktion lautet $f(x)=(2x+3)e^x$.
Zur Bestimmung der Extrema werden noch die ersten beiden Ableitungen benötigt. Dies erhält man mit der Produktregel:
$\begin{align*} f'(x)&=2e^x+(2x+3)e^x\\ &=(2x+5)e^x\\ f''(x)&=2e^x+(2x+5)e^x\\ &=(2x+7)e^x. \end{align*}$
Für Extrema muss die 1. Ableitung $0$ sein:
$\begin{align*} (2x+5)e^x&=0 &|&~e^x\neq 0\\ 2x+5&=0 &|&~-5~ |~:2\\ x_E&=-2,5. \end{align*}$
Dieses $x$ wird in die 2. Ableitung eingesetzt, um zu überprüfen, ob es sich tatsächlich um ein Extremum handelt und um welches. Dann wird $x$ in die Funktionsgleichung eingesetzt und man erhält:
- $TP(-2,5|-0,16)$.
Die einzige Funktion, die dies erfüllt ist $g(x)=(x^2-1)e^x$.
Zur Bestimmung der Extrema werden noch die ersten beiden Ableitungen benötigt. Dies erhält man mit der Produktregel:
$\begin{align*} f'(x)&=2xe^x+(x^2-1)e^x\\ &=(x^2+2x-1)e^x\\ f''(x)&=(2x+2)e^x+(x^2+2x-1)e^x\\ &=(x^2+4x+1)e^x. \end{align*}$
Für Extrema muss die 1. Ableitung $0$ sein:
$\begin{align*} (x^2+2x-1)e^x&=0 &|&~e^x\neq 0\\ x^2+2x-1&=0 &|&~\text{p-q-Formel}\\ x_{E1}&=-1+\sqrt2≈0,41\\ x_{E2}&=-1-\sqrt2≈-3,41. \end{align*}$
Beide $x$ werden in die 2. Ableitung eingesetzt, um zu überprüfen, ob es sich tatsächlich um Extrema handelt und um welche. Dann werden die $x$ in die Funktionsgleichung eingesetzt und man erhält:
- $TP(0,41|-1,25)$ sowie $HP(-2,41|0,43)$.

Ortskurve (Ortslinie) bei Parabelscharen – Beispiele
Ortskurve (Ortslinie) bei ganzrationalen Funktionen

Parabelscharen

Parabelscharen – Beispiele

Scharen von Wurzelfunktionen – Kurvendiskussion

Scharen von Exponentialfunktionen – Kurvendiskussion (1)

Scharen von Exponentialfunktionen – Kurvendiskussion (2)

Scharen von Logarithmusfunktionen – Kurvendiskussion

Schar von Winkelfunktionen – Kurvendiskussion
9.966
sofaheld-Level
6.600
vorgefertigte
Vokabeln
8.314
Lernvideos
38.636
Übungen
33.706
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Klassenstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung




 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?









sehr gute Praesentation!!! Vielen Dank!!
Bestens erklärt. Dankeschön ; )