1., 2. und 3. binomische Formel
Wenn du Summen quadrieren sollst, kannst du das Distributivgesetz anwenden – etwas schneller geht dies mit der 1. binomischen Formel.
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Die erste binomische Formel
- Herleitung der 1. binomischen Formel
- Rechnerische Herleitung der 1. binomischen Formel
- Anschauliche Herleitung der 1. binomischen Formel
Die erste binomische Formel
Unter Verwendung der ersten binomischen Formel kannst du das Quadrat einer Summe berechnen:
$(a+b)^{2}=a^{2} +2 \cdot a \cdot b +b^{2}$
In den binomischen Formeln werden Binome quadriert. Ein Binom ist die Summe oder Differenz zweier Monome. Ein Monom ist ein eingliedriger Term. Monome sind zum Beispiel $2x$ oder $4$. Ein Monom ist also ein Produkt. Dieses besteht aus einem Koeffizienten sowie einer Potenz mit einer Variablen als Basis. Die Terme in der Klammer $a+b$ werden als Binome bezeichnet.
Das Distributivgesetz definiert, wie eine Multiplikation ausgeführt wird, wenn einer der Faktoren eine Summe ist. Formal lautet das Distributivgesetz wie folgt:
$a\cdot(b+c)=a\cdot b+a\cdot c$
Die linke Seite der Gleichung sagt aus, dass du zuerst die Summe von $a$ und $b$ bildest und das Ergebnis mit $c$ multiplizierst. Die rechte Seite besagt, dass du zuerst die Faktoren multiplizierst und dann das Produkt addierst. Das Gleichheitszeichen sagt dir, dass das Ergebnis das Gleiche ist.
Herleitung der 1. binomischen Formel
Im folgenden Abschnitt siehst du nun die rechnerische Herleitung der 1. binomischen Formel, indem ausmultipliziert und das Distributivgesetz angewendet wird. Anschließend folgt die anschauliche Herleitung.
Rechnerische Herleitung der 1. binomischen Formel
Warum gilt die erste binomische Formel?
Du hast bereits gesehen, dass du den Term $(a+b)^2=(a+b)\cdot (a+b)$ mithilfe des Distributivgesetzes berechnen kannst:
$\begin{array}{rcl} (a+b)\cdot (a+b)&=&(a+b)\cdot a+(a+b)\cdot b\\ &=&a\cdot a+b\cdot a+a\cdot b+b\cdot b\\ &=&a^2+ab+ab+b^2\\ &=&a^2+2ab+b^2 \end{array}$
Wenn du bei jedem Quadrat einer Summe so rechnen musst, hast du viel zu tun. Schneller geht es, wenn du die erste binomische Formel $(a+b)^2=a^2+2ab+b^2$ verwendest.
Anschauliche Herleitung der 1. binomischen Formel
Du kannst die erste binomische Formel auch anschaulich begründen:
Hier siehst du ein grünes Quadrat mit der Seitenlänge $a+b$. Dessen Flächeninhalt beträgt $(a+b)^2$. Das ist die linke Seite der ersten binomischen Formel.
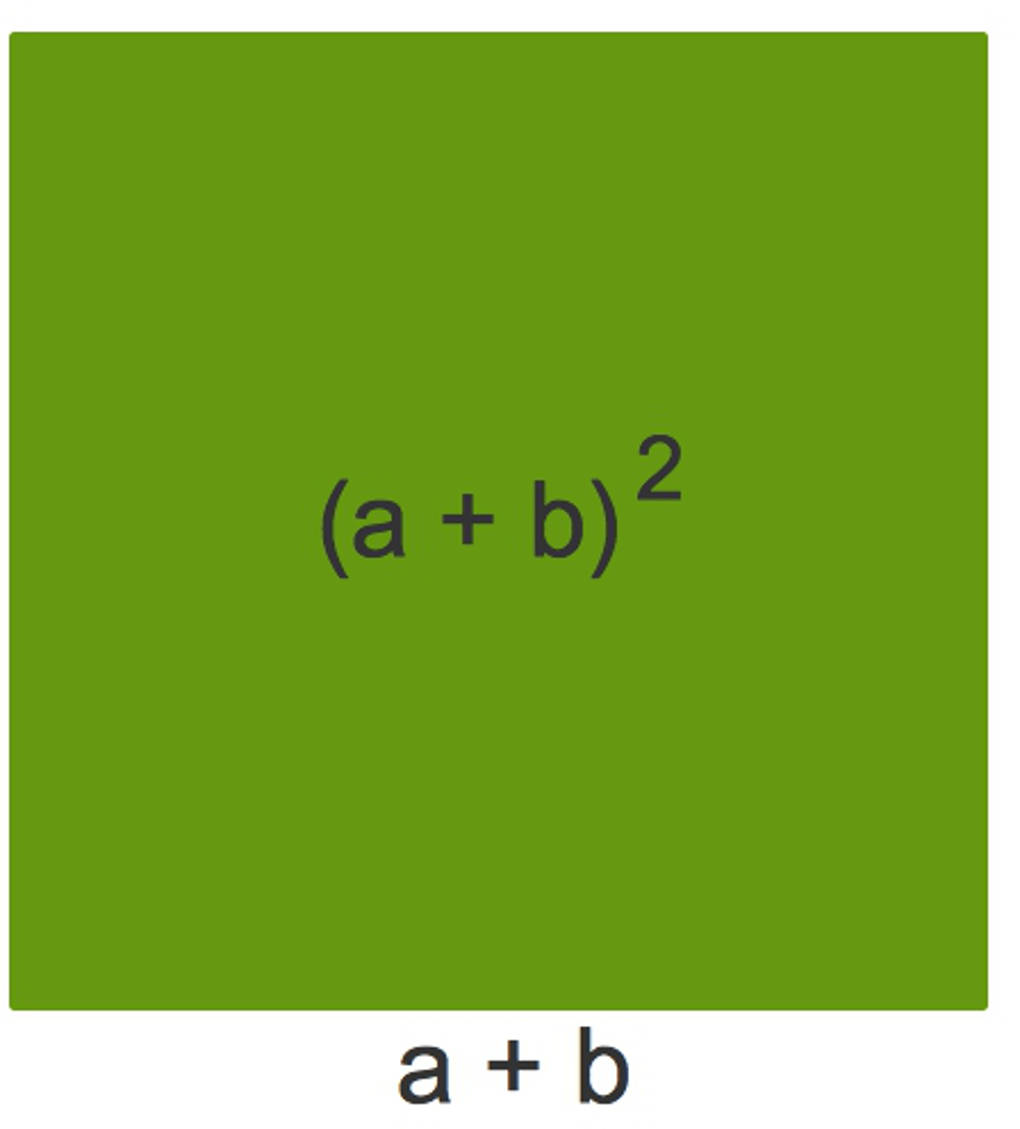
Dieses Quadrat kannst du aufteilen in das rote und das blaue Quadrat sowie zwei gelbe Rechtecke.

Das bedeutet, dass sich der Flächeninhalt des grünen Quadrates so aufteilen lässt, wie du dies hier sehen kannst.
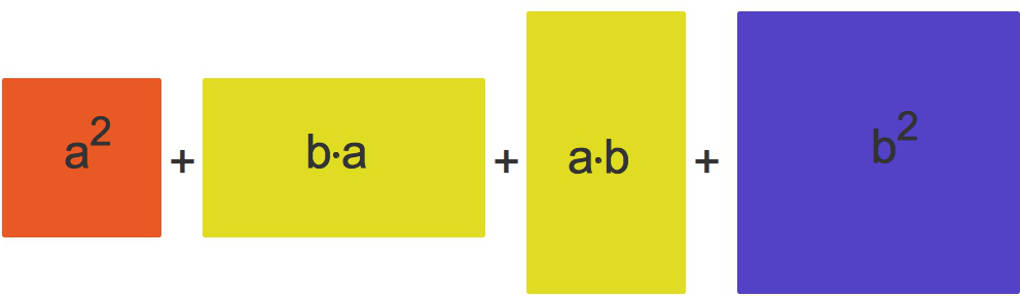
Es gilt also $(a+b)^2=a^2+b\cdot a+a\cdot b+b^2$. Mit dem Kommutativgesetz gilt $b\cdot a=a\cdot b$. Das bedeutet, dass du bei der Multiplikation die Reihenfolge der Faktoren vertauschen darfst. Nun kannst du weiter zusammenfassen: $(a+b)^2=a^2+2a b+b^2$
Anwendung der 1. binomischen Formel
Wenn du eine Summe quadrieren sollst, verwendest du die erste binomische Formel. Schau dir dies anhand von Beispielen an:
1. binomische Formel Beispiel 1
Schau du dieses Quadrat an: $(2x+3y)^2$
- Hier spielt $2x$ die Rolle von $a$ und $3y$ die von $b$.
- Du erhältst dieses Mal $(2x+3y)^2=(2x)^2+2\cdot (2x)\cdot (3y)+(3y)^2$.
- Beachte, dass du beim Quadrieren von Produkten jeden Faktor quadrieren musst:
- $(2x+3y)^2=4x^2+12xy+9y^2$
1. binomische Formel Beispiel 2
Du kannst die erste binomische Formel auch verwenden, um Quadrate von Zahlen zu berechnen:
- $102^2=(100+2)^2$
- Du kannst nun die erste binomische Formel anwenden: $(100+2)^2=100^2+2\cdot 100\cdot 2+2^2=10000+400+4=10404$
1. binomische Formel Beispiel 3
Du kannst die erste binomische Formel auch in der umgekehrten Reihenfolge anwenden. Lass uns dies einmal an dem Term $9x^2+6x+1$ üben.
- Zunächst sieht dies noch nicht so sehr nach der rechten Seite der ersten binomischen Formel aus. Schreibe den ersten und dritten Summanden jeweils als Quadrat: $(3x)^2+6x+1^2$
- Siehst du es schon?
- Wenn du den mittleren Faktor umschreibst $6x=2\cdot (3x)\cdot 1$, kannst du die erste binomische Formel erkennen. $3x$ spielt die Rolle von $a$ und $1$ die von $b$.
- $(3x)^2+2\cdot (3x)\cdot 1+1^2=(3x+1)^2$
Insgesamt erhältst du dann $9x^2+6x+1=(3x+1)^2$.
Brüche kürzen mit der 1. binomischen Formel
Du kannst nun das folgende Beispiel verwenden, um einen Bruch zu kürzen: $\frac{9x^2+6x+1}{x(3x+1)}$
Im Folgenden darf $x$ weder $0$ noch $-\frac13$ sein, da ansonsten der Nennerterm den Wert $0$ annehmen würde. Du weißt ja, dass die Division durch $0$ nicht erlaubt ist.
- Forme den Zählerterm um: $9x^2+6x+1=(3x+1)^2$
- Damit ist $\frac{9x^2+6x+1}{x(3x+1)}=\frac{(3x+1)^2}{x(3x+1)}$.
- Nun siehst du, dass das Binom $3x+1$ sowohl im Zähler- als auch im Nennerterm als Faktor auftaucht. Das bedeutet, dass du dies kürzen kannst:
- $\frac{9x^2+6x+1}{x(3x+1)}=\frac{(3x+1)^2}{x(3x+1)}=\frac{3x+1}x$
Die zweite binomische Formel
Unter Verwendung der zweiten binomischen Formel kannst du das Quadrat einer Differenz berechnen: $(a-b)^{2}=a^{2} -2 \cdot a \cdot b +b^{2}.$
Im Folgenden wirst du zum einen die Herleitung und zum anderen Anwendungen der zweiten binomischen Formel sehen.
Herleitung der zweiten binomischen Formel
Im folgenden Abschnitt siehst du nun sowohl die rechnerische Herleitung der 2. binomischen Formel mittels Ausmultiplizieren als auch die anschauliche Herleitung.
Rechnerische Herleitung der 2. binomischen Gleichung
Der Term $(a-b)^2=(a-b)\cdot (a-b)$ lässt sich mit Hilfe des Distributivgesetzes ausmultiplizieren:
$\begin{array}{rcl} (a-b)\cdot (a-b)&=&(a-b)\cdot a-(a-b)\cdot b\\ &=&a\cdot a-b\cdot a-a\cdot b+b\cdot b\\ &=&a^2-a\cdot b-a \cdot b+b^2\\ &=&a^2-2ab+b^{2} \end{array}$
Wenn du jedes Quadrat einer Differenz so berechnest, ist das sehr umständlich.Schneller kannst du die Differenz lösen, wenn du die zweite binomische Formel $(a-b)^2=a^2-2ab+b^2$ verwendest.
Anschauliche Herleitung
Du kannst die zweite binomische Formel auch anschaulich erklären.
Hier siehst du ein Quadrat mit $a-b$. Dessen Flächeninhalt beträgt $(a-b)^2$. Das ist die linke Seite der zweiten binomischen Formel.

Fügst du diesem Quadrat einige Flächenstücke hinzu, erhältst du dieses bunte Quadrat mit der Seitenlänge $a$ und dem Flächeninhalt $a^{2}$.
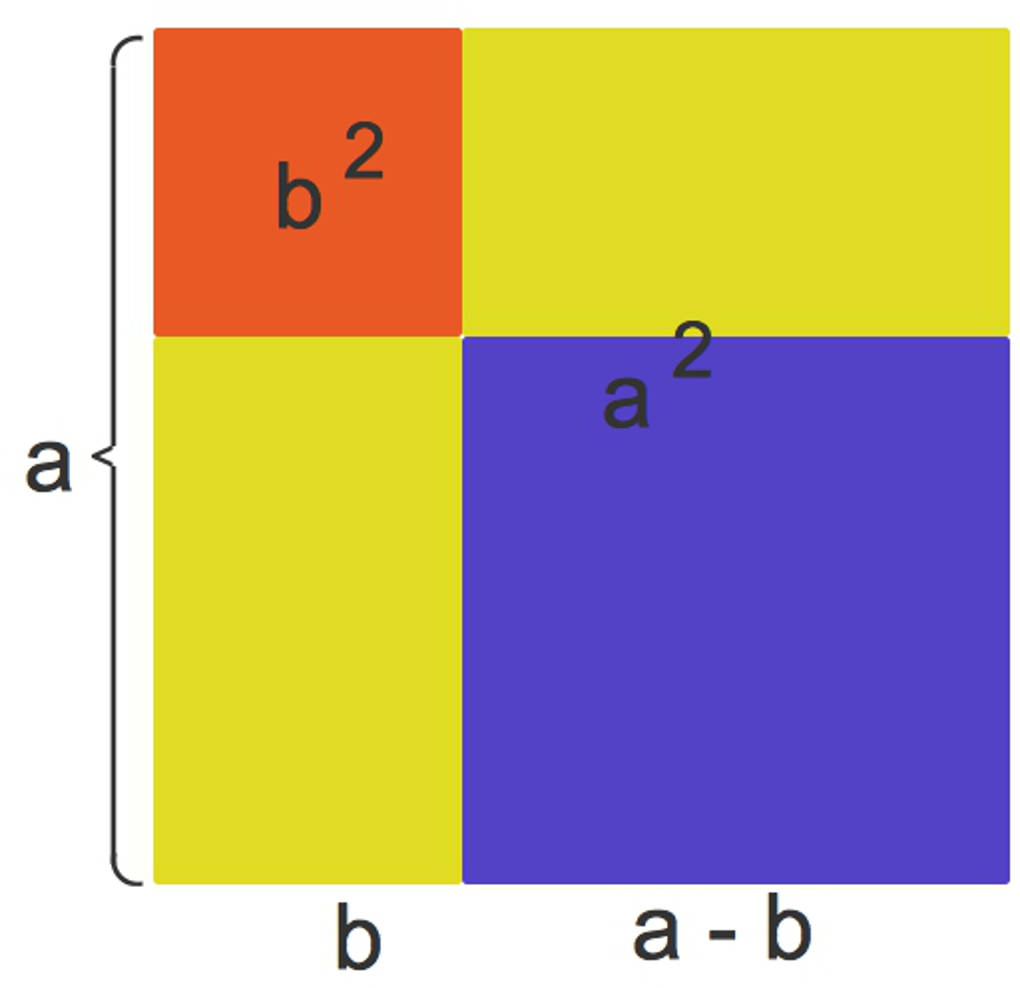
Umgekehrt bedeutet dies, dass du zweimal den Flächeninhalt der Rechtecke, welche du rot und orange gefärbt erkennst, subtrahieren musst, um wieder zu $(a-b)^{2}$ zu gelangen. Du hast dann den Flächeninhalt $b^{2}$ des roten Quadrates einmal zu oft subtrahiert. Deshalb addierst du diesen wieder:
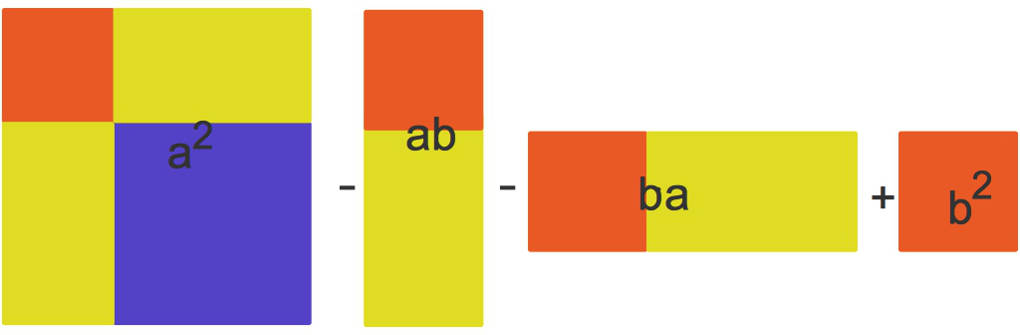
Es gilt also $(a-b)^2=a^2-a\cdot b-b\cdot a+b^2$. Mit dem Kommutativgesetz gilt $a\cdot b=b\cdot a$. Das bedeutet, dass du bei der Multiplikation die Reihenfolge der Faktoren vertauschen darfst. Nun kannst du weiter zusammenfassen: $(a-b)^2=a^2-2a b+b^2$.
Anwendung der zweiten binomischen Formel
Wenn du eine Differenz quadrieren möchtest, verwendest du die zweite binomische Formel. Im folgenden Abschnitt kannst du dein neues Wissen zur zweiten binomischen Formel an Beispielen anwenden.
2. binomische Formel Beispiel 1
Wende die zweite binomische Formel auf $(x-3)^2$ an:
- Hier spielt $x$ die Rolle von $a$ und $3$ die von $b$.
- So erhältst du $(x-3)^2=x^2-2\cdot x\cdot 3+3^2$.
- Dies kannst du noch weiter zusammenfassen zu $(x-3)^2=x^2-6x+9$.
Beachte, dass $3$ die Rolle von $b$ spielt und nicht $-3$. Wenn du $-3$ betrachtest, kannst du die erste binomische Formel anwenden.
2. binomische Formel Beispiel 2
Du kannst die zweite binomische Formel auch verwenden um Quadrate von Zahlen zu berechnen:
- $999^2=(1000-1)^2$
- Du kannst nun die zweite binomische Formel anwenden: $(1000-1)^2=1000^2-2\cdot 1000\cdot 1+1^2=1000000-2000+1=998001$
2. binomische Formel Beispiel 3
Schließlich kannst du die zweite binomische Formel auch in der umgekehrten Reihenfolge anwenden. Lass uns dies einmal an dem Term $25x^2-30x+9$ üben.
- Erkennst du bereits die rechte Seite der zweiten binomischen Formel?
- Schreibe $25x^2=(5x)^2$ sowie $9=3^2$.
- Damit ist $25x^2-30x+9=(5x)^2-30x+3^2$.
- Nun kannst du noch den mittleren Term umformen: $-30x=-2\cdot (5x)\cdot 3$.
- Schon kannst du die zweite binomische Formel anwenden: $5x$ spielt die Rolle von $a$ und $3$ die von $b$.
- $(5x)^2-2\cdot (5x)\cdot 3+9^2=(5x-3)^2$
Insgesamt erhältst du schließlich $25x^2-30x+9=(5x-3)^2$.
Brüche kürzen mit der 2. binomischen Formel
Hierfür verwendest du den Term aus Beispiel 3, um in einem Bruch zu kürzen: $\frac{x(5x-3)}{25x^2-30x+9}$.
Beachte, dass $x\neq \frac35$ sein muss. Für $\frac35$ nimmt der Nennerterm den Wert $0$ an. Die Division durch $0$ ist nicht erlaubt.
- Forme den Nennerterm um: $25x^2-30x+9=(5x-3)^2$.
- Damit ist $\frac{x(5x-3)}{25x^2-30x+9}=\frac{x(5x-3)}{(5x-3)^2}$.
- Nun siehst du, dass das Binom $5x-3$ sowohl im Zähler als auch im Nennerterm als Faktor auftaucht. Das bedeutet, dass du dies kürzen kannst:
- $\frac{x(5x-3)}{25x^2-30x+9}=\frac{x(5x-3)}{(5x-3)^2}=\frac{x}{5x-3}$.
Die dritte binomische Formel
Die dritte binomische Formel benötigst du, wenn du zwei Binome multiplizieren möchtest: $(a+b)\cdot(a-b)=a^{2} -b^{2}$.
Herleitung der dritten binomischen Formel
Du kannst die dritte binomische Formel durch Ausmultiplizieren herleiten. Ebenso kannst du diese anschaulich erklären.
Rechnerische Herleitung der dritten binomischen Formel
Du weißt bereits, wie du das Produkt $(a+b)\cdot (a-b)$ mit Hilfe des Distributivgesetzes ausrechnest:
$\begin{array}{rcl} (a+b)\cdot (a-b)&=&(a+b)\cdot a-(a+b)\cdot b\\ &=&a\cdot a+b\cdot a-a\cdot b-b\cdot b\\ &=&a^2-ab+ab-b^2\\ &=&a^2-b^2 \end{array}$
Nun ist es sehr aufwändig, jedes Mal so zu rechnen. Deshalb verwendest du die dritte binomische Formel: $(a+b)\cdot (a-b)=a^2-b^2$
Anschauliche Herleitung der dritten binomischen Formel
Du kannst die dritte binomische Formel auch anschaulich erklären:
Du startest mit einem Rechteck mit den Seitenlängen $a+b$ und $a-b$. Der Flächeninhalt dieses Rechtecks beträgt $(a+b)\cdot (a-b)$. Dies ist die linke Seite der dritten binomischen Formel.
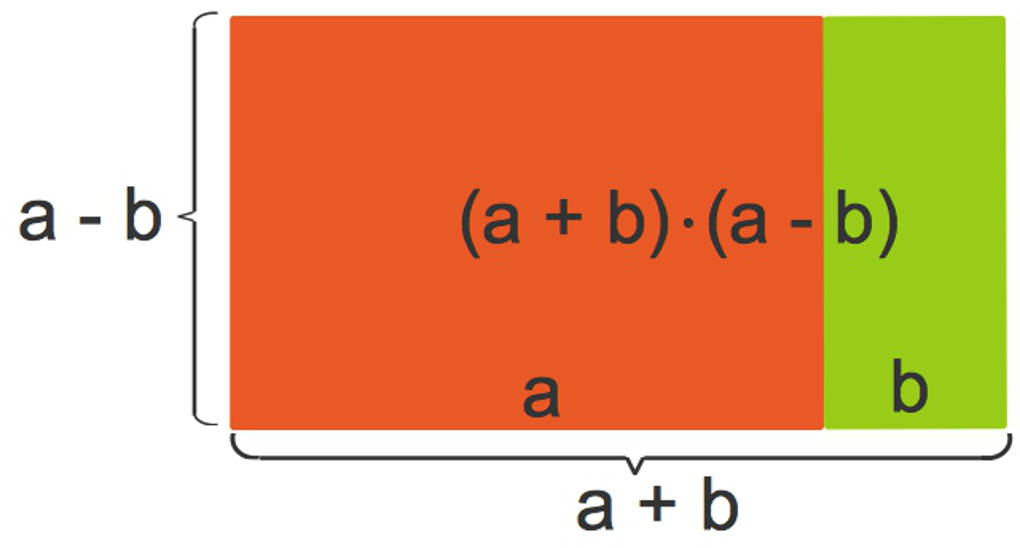
Das grüne Rechteck rechts wird ausgeschnitten und oben an das Ausgangsrechteck angefügt.
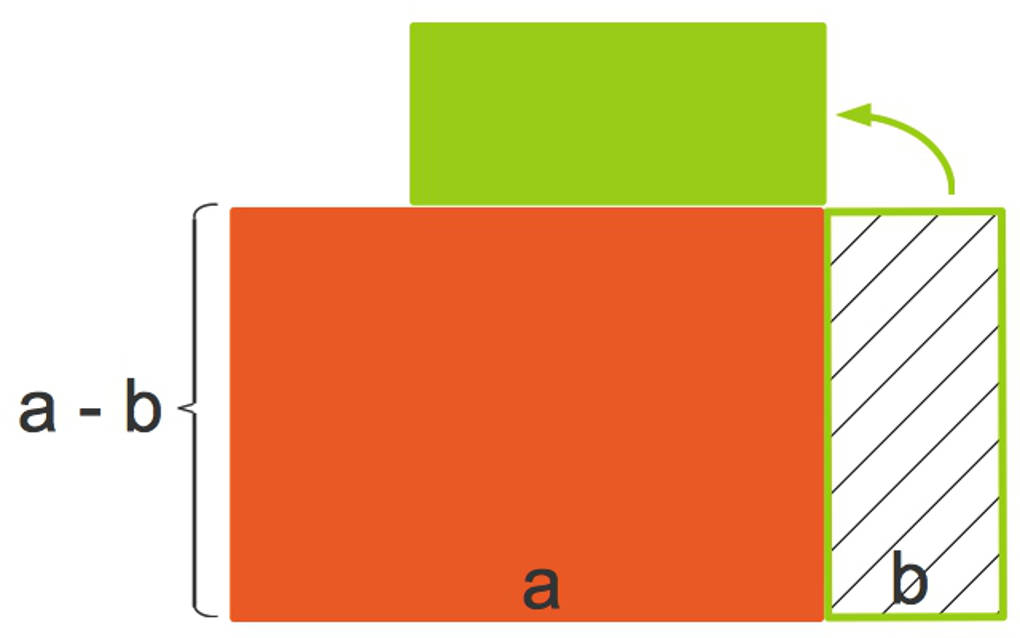
Wenn du nun noch das orange Quadrat mit dem Flächeninhalt $b^{2}$ zufügst, erhältst du ein Quadrat mit den Seitenlängen $a$ und dem Flächeninhalt $a^{2}$.
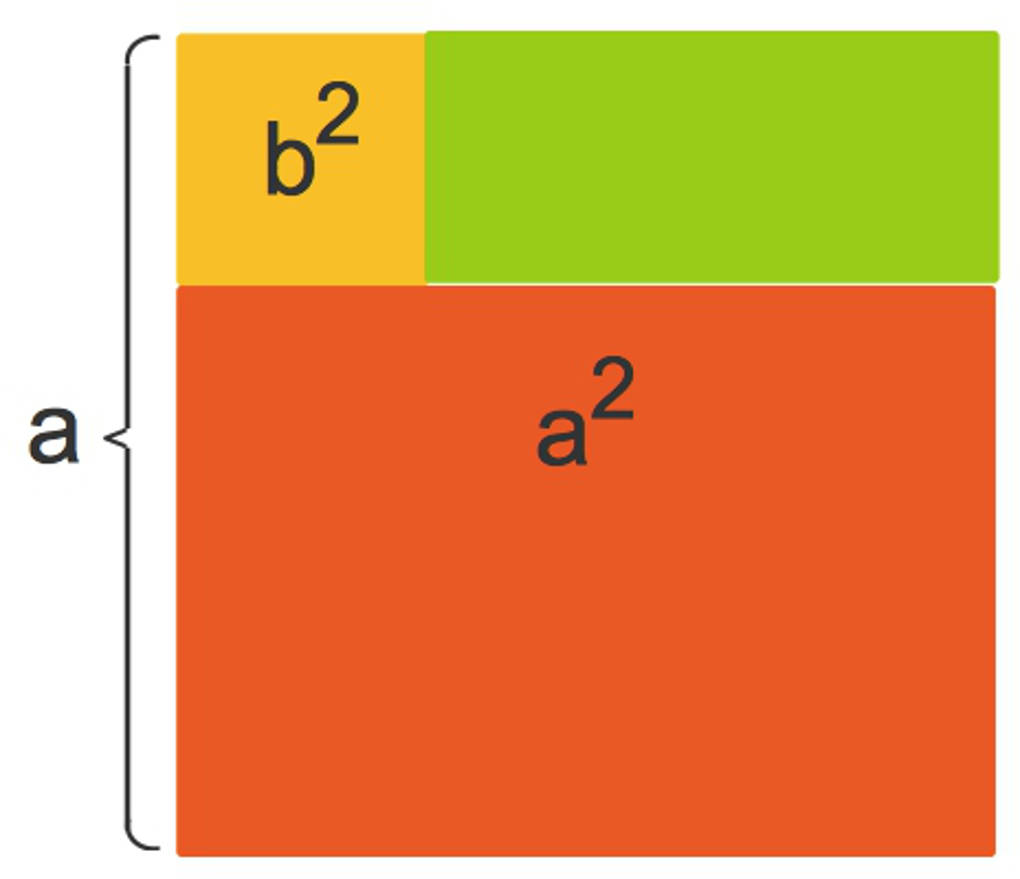
Gesamt gilt dann $a^2=(a+b)\cdot (a-b)+b^2$. Subtrahiere nun auf beiden Seiten $b^2$. Dies führt zu $(a+b)\cdot (a-b)=a^2-b^2$.
Anwendungsaufgaben der 3. binomischen Formel
Wenn du die Summe zweier Monome mit der Differenz dieser beiden Monome multiplizieren sollst, verwendest du die dritte binomische Formel.
3. binomische Formel Einstiegsbeispiel
Schau dir dieses Produkt an: $(4x+5z)\cdot (4x-5z)$
- Hier spielt $4x$ die Rolle von $a$ und $5z$ die von $b$.
- Du erhältst somit $(4x+5z)\cdot (4x-5z)=(4x)^2-(5z)^2$.
- Beachte, dass du beim Quadrieren von Produkten jeden Faktor quadrieren musst:
- $(4x+5z)\cdot (4x-5z)=16x^2-25z^2$
3. binomische Formel zur Bestimmung des Produktes zweier Zahlen
Du kannst die dritte binomische Formel auch verwenden um das Produkt zweier Zahlen zu berechnen:
- $53\cdot 47=(50+3)\cdot (50-3)$
- Du kannst nun die dritte binomische Formel anwenden: $(50+3)\cdot (50-3)=50^2-3^2=2500-9=2491$.
3. binomische Formel in umgekehrter Reihenfolge
Du kannst die dritte binomische Formel auch in der umgekehrten Reihenfolge anwenden. Du erkennst die rechte Seite der dritten binomischen Formel daran, dass dort die Differenz zweier Quadrate steht. Lass uns dies einmal an dem Term $25x^2-16a^2$ üben.
- Erkennst du bereits die rechte Seite der dritten binomischen Formel?
- Schreibe $25x^2=(5x)^2$ sowie $16a^2=(4a)^2$.
- Damit ist $25x^2-16a^2=(5x)^2-(4a)^2$.
- Jetzt kannst die dritte binomische Formel anwenden: $5x$ spielt die Rolle von $a$ und $4a$ die von $b$.
- $25x^2-16a^2=(5x)^2-(4a)^2=(5x+4a)\cdot(5x-4a)$
Insgesamt erhältst du schließlich $25x^2-16a^2=(5x+4a)\cdot(5x-4a)$.
Brüche kürzen mit der 3. binomischen Formel
Schau dir den Bruch $\frac{x(5x+4a)}{25x^2-16a^2}$ an. Wenn du den Nennerterm faktorisierst, kannst du den Bruch zu kürzen:
Beachte, dass $x\neq \pm\frac{4}{5}a$ sein muss. Andernfalls würde der Nennerterm den Wert $0$ annehmen und du weißt sicher, dass du durch $0$ nicht dividieren darfst.
- Forme den Nennerterm um: $25x^2-16a^2=(5x+4a)\cdot (5x-4a)$.
- Damit ist $\frac{x(5x+4a)}{25x^2-16a^2}=\frac{x(5x+4a)}{(5x+4a)\cdot (5x-4a)}$.
- Nun siehst du, dass das Binom $5x+4a$ sowohl im Zähler- als auch im Nennerterm als Faktor auftaucht. Das bedeutet, dass du diesen kürzen kannst:
- $\frac{x(5x+4a)}{25x^2-16a^2}=\frac{x(5x+4a)}{(5x+4a)\cdot (5x-4a)}=\frac{x}{5x-4a}$.
Alle Videos zum Thema
Videos zum Thema
1., 2. und 3. binomische Formel (7 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
1., 2. und 3. binomische Formel (7 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung










 Binomische Formeln – Überblick
Binomische Formeln – Überblick
 Erste binomische Formel
Erste binomische Formel
 Zweite binomische Formel
Zweite binomische Formel
 Dritte binomische Formel
Dritte binomische Formel
 Die binomischen Formeln
Die binomischen Formeln
 Binomische Formeln – Übungen
Binomische Formeln – Übungen
 Binomische Formeln: Faktorisieren
Binomische Formeln: Faktorisieren









